2. 西伯利亚联邦大学热技术与流体动力学系, 克拉斯诺亚尔斯克 660041
2. Department of Heat Technology and Fluid Dynamics, Siberian Federal University, Krasnoyarsk 660041, Russia
当前淡水资源匮乏已成为全球性的环境问题,相比于另外两种淡水取用方式——地下取水和远程调水,海水淡化以其能耗低、来源广和资源丰富等优点被认为是最具前景的淡水取用方式.目前海水淡化技术主要有热蒸馏法和膜方法,而工业上大规模应用的是热蒸馏法中的多级闪蒸和低温多效蒸馏以及膜方法中的反渗透法.但是,由于热蒸馏法的换热面为固体壁面,因而存在能量密度低和换热面易形成水垢和污垢等缺点,而反渗透法则需要对源水进行严格的预处理.为克服上述缺点,应用超空泡原理,提出一种新型的海水淡化装置——旋转超空泡蒸发器(rotational supercavitating evaporator,简称RSCE).RSCE的核心部件是由两个出口边宽度变化的楔形叶片组成的旋转空化器,空化器在盐水中高速旋转形成超空泡,在叶片根部的适当位置设置抽汽孔用于抽取空化形成的水蒸汽,经冷凝后形成淡水.
空化是液体在温度基本保持不变的情况下由于压力降低而发生汽化,使液体内部的气核迅速膨胀,形成含有水蒸气或其他气体的明显气(汽)泡,从而造成液体破裂的现象.通常采用空化数来描述空化流动,流动中特征压力越低或特征速度越大,则空化数越小,空化程度越剧烈.超空泡即是小空化数下发生的一种完全发展的附着空泡,其尾部在过流部件固体边界下游闭合,空泡长度大于过流部件的特征长度.目前,绝大部分对空化在海水淡化中应用的研究主要集中在俄罗斯,但鲜见公开发表的相关文献.其中一个例子是俄罗斯TJEROS-MIFI科技中心设计的商用空化海水淡化装置WATERFALL-1200[1].最近,Likhachev等[2-4]提出RSCE,并进行了初步的设计和研究.旋转空化常见于螺旋桨、水轮机和泵等流体机械中,有大量的实验观测和理论分析对其进行了研究[5-6],但是针对从空泡中抽取蒸汽对空泡形状和尺寸影响的研究则很少.Likhachev和Li[7]通过对圆锥型空化器超空泡流动进行二维数值模拟,发现从超空泡中抽取蒸汽将增强空泡尾部的回射流,从而减小超空泡的轴向尺寸,并在径向上撑大超空泡体积,但是其增大的幅度比轴向尺寸减小的幅度小,因而超空泡表面积将减小,引起蒸汽生成率的降低,进而导致超空泡的缩短.而Likhachev等[4]对RSCE进行抽汽实验的结果表明,在实验设定的抽汽参数范围内,蒸汽抽取对超空泡尺寸影响很小.
本文在Likhachev和Li提出RSCE并进行初步研究的基础上,从抽汽参数的角度对其进行优化,为达到提供实验参数的目的,针对不同抽汽量下的三维RSCE超空泡流动进行数值模拟,获得了合适的抽汽孔位置,分析不同工况下超空泡的尺寸以及抽汽量对超空泡形态的影响,以此指导实验中抽汽参数的设定和真空泵的选取.
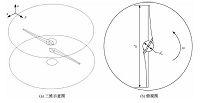
1 模型建立旋转空化器如图 1所示.根据实验装置的具体尺寸[4],选取高为100mm,直径为430mm的圆柱体区域作为计算域.旋转空化器直径d为400mm,转轴直径d0为52mm,叶片旋转平面位于计算域正中间.
|
Download:
|
| 图 1 旋转空化器示意图 Fig. 1 Schematic diagram of RSCE | |
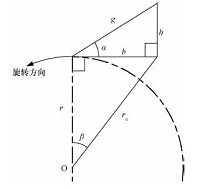
为获得旋转空化器的叶片形状,采用与文献[3]中相同的公式对其进行计算,但是原方法中不同半径r处α值并不严格等于对应半径处的楔形角(22.5°),且随着r的减小,其偏差越大.针对这一问题,提出如图 2所示的改进的计算方法,用rc替代r计算得到的超空泡长度L和圆弧长度进行比较,从而得到改进的旋转空化器叶形,如表 1所示.此外,表 1中也给出了由经验公式(1)[3]得到的不同r处的超空泡长度L.
| $L=\left( 2.6h/\sigma \right)\sqrt{{{C}_{\text{d}}}/e},$ | (1) |
式中,h为叶片出口边半高;σ为空化数,其定义为σ=2(p0-pc)/ρv2,其中p0为环境压力,pc为超空泡内压力,计算中其值等于饱和蒸汽压,ρ为水的密度,v为叶片线速度;Cd为阻力系数,其值为Cd=0.175+0.3σ;e为经验系数,定义为e=(1+50σ)/(1+56.2σ).
|
Download:
|
| 图 2 旋转空化器叶片形状计算方法示意图 Fig. 2 Calculation method for blade shape of RSCE | |
|
|
表 1 旋转空化器叶片形状参数 Table 1 Calculation method for blade shape of RSCE |
本文针对三维RSCE定常超空泡流动进行数值模拟,而超空泡流动是一种多相、湍动的复杂流动,在数值模拟中多相流模型采用基于均匀平衡多相流理论的混合模型,将气相和液相的混合物看成均匀的单相流体,其控制方程为:
混合相连续性方程
| $\frac{\partial }{\partial {{x}_{i}}}\left( {{\rho }_{\text{m}}}{{u}_{i}} \right)=0,$ | (2) |
混合相动量方程
| $\begin{align} & \frac{\partial \left( {{\rho }_{\text{m}}}{{u}_{i}}{{u}_{j}} \right)}{\partial {{x}_{j}}}=-\frac{\partial p}{\partial {{x}_{i}}}+ \\ & \frac{\partial }{\partial {{x}_{j}}}\left[ \left( {{\mu }_{\text{m}}}+{{\mu }_{t}} \right)\left( \frac{\partial {{u}_{i}}}{\partial {{x}_{j}}}+\frac{\partial {{u}_{j}}}{\partial {{x}_{i}}}-\frac{2}{3}\frac{\partial {{u}_{k}}}{\partial {{x}_{k}}}{{\delta }_{ij}} \right) \right], \\ \end{align}$ | (3) |
气相输运方程
| $\frac{\partial }{\partial {{x}_{i}}}\left( {{\alpha }_{\text{v}}}{{\rho }_{\text{v}}}{{u}_{i}} \right)={{R}_{\text{e}}}-{{R}_{\text{c}}}$ | (4) |
式中,ρm为混合相密度,ui或uj为速度,αv为气相体积分数,ρv为气相密度,Re和Rc分别为气相生成率和气相凝结率.
空化模型采用Schnerr-Sauer模型[8],给出相变率Re和Rc的方程:
当pv≥p时,
| ${{R}_{\text{e}}}\text{=}\frac{{{\rho }_{\text{v}}}{{\rho }_{\text{1}}}}{{{\rho }_{\text{m}}}}{{\alpha }_{\text{v}}}\left( 1-{{\alpha }_{\text{v}}} \right)\frac{3}{{{R}_{\text{B}}}}\sqrt{\frac{2}{3}\frac{\left( {{\rho }_{\text{v}}}-p \right)}{{{\rho }_{\text{1}}}}};$ | (5) |
当pv≤p时,
| ${{R}_{\text{e}}}\text{=}\frac{{{\rho }_{\text{v}}}{{\rho }_{\text{1}}}}{{{\rho }_{\text{m}}}}{{\alpha }_{\text{v}}}\left( 1-{{\alpha }_{\text{v}}} \right)\frac{3}{{{R}_{\text{B}}}}\sqrt{\frac{2}{3}\frac{\left( p-{{\rho }_{\text{v}}} \right)}{{{\rho }_{\text{1}}}}}.$ | (6) |
式中,ρl为液相密度;pv为饱和蒸汽压;n为液体单位体积中的微小气泡数,其值为1×1013;RB为气泡半径,该空化模型中其定义式为
| ${{R}_{\text{B}}}={{\left( \frac{{{\alpha }_{\text{v}}}}{1-{{\alpha }_{\text{v}}}}\frac{3}{4\pi }\frac{1}{n} \right)}^{\frac{1}{3}}}.$ | (7) |
湍流模型采用Realizable k-ε模型,其模型方程为:
| $\frac{\partial \left( \rho k{{u}_{i}} \right)}{\partial {{x}_{i}}}=\frac{\partial }{\partial {{x}_{j}}}\left[ \left( \mu +\frac{{{\mu }_{t}}}{{{\sigma }_{k}}} \right)\frac{\partial k}{\partial {{x}_{j}}} \right]+{{G}_{k}}-\rho \varepsilon ,$ | (8) |
| $\frac{\partial \left( \rho \varepsilon {{u}_{i}} \right)}{\partial {{x}_{i}}}=\frac{\partial }{\partial {{x}_{j}}}\left[ \left( \mu +\frac{{{\mu }_{t}}}{{{\sigma }_{\varepsilon }}} \right)\frac{\partial \varepsilon }{\partial {{x}_{j}}} \right]+\rho {{C}_{1}}S\varepsilon -\rho {{C}_{2}}\frac{{{\varepsilon }^{2}}}{k+\sqrt{v\varepsilon }},$ | (9) |
式中,σk=1.0,σε=1.2,
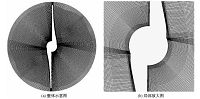
采用结构化网格对计算域进行划分,同时对叶片附近网格进行加密处理,如图 3所示,网格数量为8159268.计算中建立的笛卡尔直角坐标系如图 1(a)所示,y轴位于叶片进口边所在直线,z轴为旋转轴线.计算域上表面和底面分别设置为压力入口和压力出口边界条件,压力均设定为101325Pa,圆柱面设置为固定无滑移壁面边界条件,其他边界均设置为具有恒定转速的无滑移壁面.水和水蒸气物性参数采用国际IAPWS95标准[9],25℃时水的物性为:密度997kg/m3,动力黏度8.9011×10-4Pa·s;水蒸气的物性为:密度0.023075kg/m3,动力黏度9.8669×10-6Pa·s;饱和蒸汽压pv为3169.9Pa.
|
Download:
|
| 图 3 网格划分示意图 Fig. 3 Schematic diagram of mesh | |
通过初步试算得到未抽汽工况下当转速为4500r/min时空化器后方形成具有最大尺寸的超空泡,通过分析气相体积分数分布确定抽汽孔的位置.在此基础上针对不同抽汽压力下的三维RSCE超空泡流动进行数值模拟,通过分析超空泡表面积和体积,得到抽汽量对超空泡尺寸的影响,以此对后续实验中抽汽参数的选取进行指导.
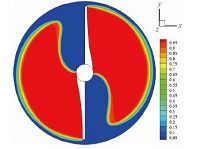
3.1 未抽汽工况计算结果及抽汽孔位置选取图 4给出z=0m平面水蒸气体积分数分布,从图中可看出其分布呈对称的扇形.为对超空泡进行定量分析,将水蒸气体积分数为0.5的等值面定义为超空泡的轮廓,则其轮廓如图 5所示.通过进一步计算得到超空泡的面积和体积分别为0.20862m2和2.277×10-3m3,从图中可看出,当半径较小时,超空泡尾部有明显的回射流,如图 5(b)所示.而回射流会将水滴夹带到超空泡中,若将抽汽孔设置在靠近超空泡尾部的位置,将大大影响抽取的水蒸气的纯度,因此根据这一计算结果将直径为6mm的抽汽孔设置在与叶片进口边所在直线(y轴)成30°角的位置,如图 1(b)所示.
|
Download:
|
| 图 4 z=0m平面水蒸气体积分数分布 Fig. 4 Distribution of vapor volume fraction in the plane at z=0m | |

|
Download:
|
| 图 5 超空泡轮廓示意图 Fig. 5 Supercavity profile | |
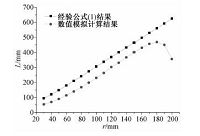
以上述定义为基础得到的超空泡长度随半径的变化如图 6所示,图中也给出了经验公式(1)的计算结果进行对比.从图中可看出,当半径小于180mm时,经验公式得到的结果和数值模拟的结果有较好的符合,均随半径增大呈现近似线性的增大,而半径大于180mm后,则有较大的差距.这是由于经验公式是由楔形空化器平面流动得到的,没有考虑旋转带来的影响,同时圆柱壁面也会对超空泡的发展起到约束作用,因而造成大半径下结果的较大偏差.
|
Download:
|
| 图 6 超空泡长度经验公式和数值模拟结果对比 Fig. 6 Calculated results for supercavity lengths at different radii and comparison of these results with those using empirical formula | |
为模拟不同抽汽量下的三维RSCE超空泡流动,将抽汽孔设置为压力低于饱和蒸汽压的压力出口边界条件,分别计算压力为0,1000和2000Pa 3个工况,从而得到不同抽汽压力P下的抽汽量Q,如表 2所示,抽汽量随抽汽压力的降低而线性增大.此外,表 2中还给出不同抽汽压力下抽汽孔的液态水体积分数平均值,从一定程度上反映抽取的蒸汽的纯度.从表中可看出,虽然液态水体积分数平均值随抽汽压力的降低而增大,但是其值始终维持在较低的量级,说明抽取的蒸汽纯度很高,也进一步证明抽汽孔位置设置的合理性.
|
|
表 2 不同抽汽压力P下的抽汽量Q和抽汽孔水体积分数 Table 2 Steam extraction rate Q and water volume fraction at the extraction hole under different extraction pressure P |
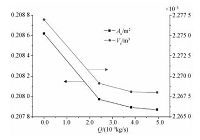
图 7给出不同抽汽量下超空泡的面积Ac和体积Vc,抽汽量为零的结果对应于未抽汽工况.从图中可看出,抽汽对超空泡的面积和体积有较大影响,但是在抽汽的情况下,超空泡面积和体积随抽汽量的增大只有略微减小,且进一步的数值模拟结果表明,即使低于饱和蒸汽压,当抽汽压力较大时,并没有抽汽现象,这一阈值的确定将在后续研究中给出.
|
Download:
|
| 图 7 超空泡面积Ac和体积Vc随抽汽量Q的变化 Fig. 7 Variations in supercavity area Ac and volume Vc with steam extraction rate Q | |
通过对不同抽汽量下的三维RSCE超空泡流动进行数值模拟,得到超空泡的轮廓以及不同工况下超空泡的面积和体积,分析水蒸气体积分数分布和抽汽对超空泡尺寸的影响,确定了合适的抽汽孔位置,得到以下主要结论:
1) 未抽汽工况下,半径较小处的超空泡尾部存在明显的回射流,因而将抽汽孔设置在与叶片进口边所在直线成30°角的位置处.在大部分半径范围内,超空泡长度的数值模拟结果和经验公式得到的结果有较好的符合.
2) 抽汽情况下,抽汽量随抽汽压力的降低而线性增大,相比未抽汽工况,抽汽对超空泡的面积和体积有较大影响,但抽汽后抽汽量的变化对超空泡面积和体积的影响较小.
| [1] | Rudenko B. How to make up water resource[J/OL]. Journal of Science Life, 2007, 12, (2011-10-02)[2015-02-15]. http://www.nkj.ru/archive/articles/12366/ (in Russian). |
| [2] | Likhachev D S, Li F C. Large-scale water desalination methods: a review and new perspectives[J]. Desalination and Water Treatment , 2013, 51 (13/15) :2836–2849. |
| [3] | Likhachev D S, Li F C. Modeling of rotational supercavitating evaporator and the geometrical characteristics of supercavity within[J]. Science China: Physics, Mechanics & Astronomy , 2014, 57 (3) :541–554. |
| [4] | Likhachev D S, Li F C, Kulagin V A. Experimental study on the performance of a rotational supercavitating evaporator for desalination[J]. Science China: Technological Sciences , 2014, 57 (11) :2115–2130. DOI:10.1007/s11431-014-5631-0 |
| [5] | Brennen C E. Cavitation and bubble dynamics[M]. Oxford: Oxford University Press, 1995 . |
| [6] | 潘中永, 袁寿其. 泵空化基础[M]. 镇江: 江苏大学出版社, 2013 . |
| [7] | Likhachev D S, Li F C. Numerical study of the characteristics of supercavitation on a cone in a stationary evaporator[J]. Desalination and Water Treatment , 2014, 52 (37/39) :7053–7064. |
| [8] | Schnerr G H, Sauer J. Physical and numerical modeling of unsteady cavitation dynamics[C]//Fourth International Conference on Multiphase Flow. New Orleans, USA, 2001. |
| [9] | Wagner W, Pruβ A. The IAPWS formulation 1995 for the thermodynamic properties of ordinary water substance for general and scientific use[J]. Journal of Physical and Chemical Reference Data , 2002, 31 (2) :387–535. |
 2016, Vol. 33
2016, Vol. 33 


