悬浮颗粒与流体之间的相互作用机理研究一直是多相流领域中的热点问题，流体颗粒系统广泛存在于化工、环境、能源、生命科学等领域，其与流化床、燃烧、颗粒悬浮等应用密切相关.研究悬浮颗粒运动中颗粒聚集及扩散机理对于解决实际应用中的问题起到很重要的作用.无论是从应用角度还是从基础研究角度，研究流体与悬浮颗粒之间相互作用都非常重要，因此吸引了众多研究者进行实验以及模拟方面的研究^[1-3].

在过去的几十年中，研究颗粒沉降的过程发现颗粒尾涡对颗粒的运动产生重要的影响作用，其中最重要的是由2颗粒间相互作用而发生的“拖曳-碰撞-翻滚”(DKT)运动.这种相互作用最早由Fortes et al.^[4]试验发现.在被发现之后，DKT运动被众多的研究复现，包括实验研究^[5]，直接数值模拟(DNS)^[6-7]以及格子Boltzmann(LB)模拟^[8].

实际的颗粒悬浮系统包含数量非常巨大的有限体积的颗粒，因此研究实际悬浮颗粒与流体的相互作用是非常复杂及困难的，并且计算效率很低.但是，在模拟中全解析颗粒周围的流场，并准确捕捉颗粒的运动规律对于研究颗粒与流场及颗粒间相互作用非常重要.Johnson和Tezduyar ^[9]利用全解析数值模拟方法模拟100个颗粒在三维通道中的运动.Pan et al.^[10]模拟研究1204个圆球颗粒的流化运动规律.Kajishima ^[11]采用DNS研究2048个颗粒悬浮运动中颗粒群与湍流场的相互作用.Yin和Koch^[12]研究悬浮固体颗粒在雷诺数为1~20范围内的颗粒群受阻沉降速度规律及相应的微观结构.Cao et al^[13]用格子Boltzmann方法详细分析2颗粒在不同初始状态下颗粒相互作用的关系.

从上面的研究进展中可以看到颗粒悬浮运动中颗粒与流场相互作用起到重要作用，并且对多颗粒悬浮运动的研究还很有限.因此，本文详细研究多颗粒悬浮运动的规律，并试图了解颗粒与流场的相互作用对颗粒运动产生的影响.本文采用格子Boltzmann方法及EBF曲边界处理格式研究三维大流场(全周期边界)中多颗粒的悬浮运动过程，解析颗粒周围的流场，并且捕捉颗粒的运动规律，详细分析颗粒群运动过程中相关统计量的规律.

1 格子Boltzmann方法简介

格子Boltzmann方法是以编程简单、天然并行、易于处理复杂边界为特色的介观方法，数十年来，格子Boltzmann方法在复杂流动等领域有了很大发展^{[1, 14]}.本文采用LBGK模型进行模拟，速度模型是D3Q15，详细介绍见文献^{[1, 14-15]}.对于边界处理部分，考虑到Wu和Aidun^[16]提出的附加边界应力方法非常适合于处理运动边界，本文球形曲面边界处理均使用该方法，详见文献^{[1, 16]}.颗粒碰撞部分的处理采用Glowinski et al.^[7]提出的处理方法，该方法假设当2颗粒间的距离小于给定的阀值时，颗粒间将产生排斥作用力，避免颗粒边界相互穿透，详细分析见文献^[7].

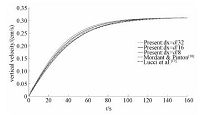
2 数值方法验证 2.1 三维单颗粒沉降验证

单颗粒在无限大流场区域沉降是一个经典问题，有许多学者对此问题进行了研究，本文将就此问题对模型进行验算，其计算域为12.5d×12.5d×100d，球形颗粒直径为d=0.8cm，流体与颗粒的密度分别为ρ_f=1.0g/cm³、ρ_p=7.71g/cm³,流体运动黏度为ν=0.009cm²/s，重力加速度为g=981cm/s².图 1给出不同网格分辨率情况下，颗粒沉降速度随时间变化的曲线图，并与文献^[17-18]结果进行对比，在网格分辨率为dx=d/8、d/16、d/32(dx为计算网格间距)时的误差分别为1.62%、0.58%和0.48%，但是dx=d/32的计算量偏大，因此在保证计算精度的情况下，考虑计算效率则选择dx=d/8或d/16作为后面计算中的网格分辨率.

2.2 三维双颗粒沉降验证

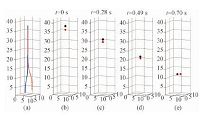
在讨论多颗粒沉降的特性之前，首先对双颗粒沉降进行验证，计算域为6d×6d×60d，d=1/6cm，网格分辨率为dx=d/16.在初始时刻，2颗粒的位置分别为(3d，3d，27d)及(3d，3d，25d).本算例中，ρ_f=1.0g/cm³，ρ_p=1.14g/cm³，ν=0.01cm²/s，重力加速度为g=981cm/s².图 2给出2颗粒的运动轨迹及不同时刻颗粒的位置图，可以明显地看出后面颗粒追赶前面颗粒(Drafting)，经过一段时间后，后面颗粒追赶上前面颗粒并碰撞(Kissing)，2颗粒一起向下运动并发生翻转(Tumbling)，最后2个颗粒分开，这种现象即为DKT现象^{[3, 7, 10-11, 13]}.

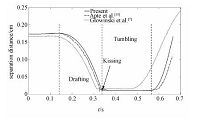
由图 3可以看出两表面颗粒之间的距离随时间变化曲线与Apte et al.^[19]的结果比较符合，虽然2颗粒分离时刻相对于Glowinski et al.^[7]的结果有所延迟，但是可以看出程序可以很好地捕捉到DKT现象，并很好地模拟颗粒运动及颗粒间相互作用.

3 数值模拟结果及分析 3.1 三维多颗粒沉降速度及统计量分析

正如前面提到的，多颗粒沉降过程中的颗粒运动及颗粒流场相互作用是很重要的研究方向，颗粒运动规律背后的机制研究仍然不够.本部分模拟研究144个颗粒和1152个颗粒的沉降过程，给出颗粒平均沉降速度、流场平均速度、颗粒群平均各向速度、颗粒群平均动能和颗粒群脉动速度等相应统计值，借此来研究多颗粒的运动规律，并试图解释背后存在的机理.

本节的1152等大小颗粒群模拟计算域为8d×8d×32d，流体网格分辨率为dx=d/8，计算域的3个方向均为周期性边界，因此当颗粒穿过边界后将从对面的边界再次回到区域内.流体密度、颗粒直径、重力加速度依次为ρ_f=1.0g/cm^-3、d=1/6cm、g=981cm/s²，沉降颗粒密度与流体密度的比为1.14.流体运动黏度为ν=0.01cm²/s.初始时刻，颗粒群在计算域中均匀分布，2个相邻颗粒间的距离为2d.

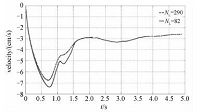
图 4给出不同球面拉格朗日网格点数(N_L=290、82)对颗粒沉降速度结果的影响，图中所显示速度为颗粒群相对于流体的速度，拉格朗日分辨率的影响主要体现在颗粒群最大沉降速度上面，N_L=82时颗粒群在受到各自尾涡的影响下加速过程更长，且受到的阻力更小(数值计算上)，故而最大速度变大，但经过各颗粒强烈的碰撞后，大体上都达到3cm/s速度.由于我们更多地关注颗粒群体系稳定后的状态，由于计算资源有限，所以我们采取N_L=82对颗粒群系统进行了较长时间的运算，后续结果不加说明情况下均为N_L=82时所得.同时，图 4也清晰地显示颗粒群经历了最初的线性加速、颗粒相互影响的非线性加速、颗粒相互作用造成的减速过程和振荡过程，与之前的研究规律一致.

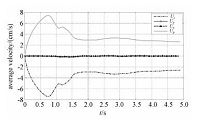
图 5给出颗粒群x、y、z方向平均速度与合速度，可以发现：颗粒群主要在z方向(即沉降方向)上有较大速度和波动，U_z与合速度U_p大致相等，在某种意义上来说x、y方向分速度对合速度U_p的贡献几乎可以忽略.

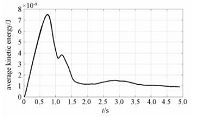
从图 6可以看出颗粒群系统开始由势能向动能转化，系统动能上升，之后由于颗粒碰撞以及颗粒与流体相互作用等使得颗粒系统平均动能减少，之后系统平均动能稳定在1×10^-9J左右，由此也可以说明之后较长时间段内颗粒群系统处于一个相对稳定的状态.

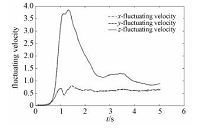
本节还对颗粒沉降运动进行了统计量的分析，颗粒的脉动速度是用来反映颗粒速度偏离颗粒群平均速度的程度，本文用颗粒的离散速度的标准差来定义颗粒的脉动速度：$\upsilon {{'}_{x}}=\sqrt{\frac{\sum\nolimits_{p=1}^{N}{{{\left( {{\upsilon }_{x,p}}-{{{\bar{\upsilon }}}_{x}} \right)}^{2}}}}{N}},$$\upsilon {{'}_{y}}=\sqrt{\frac{\sum\nolimits_{p=1}^{N}{{{\left( {{\upsilon }_{y,p}}-{{{\bar{\upsilon }}}_{y}} \right)}^{2}}}}{N}},$$\upsilon {{'}_{z}}=\sqrt{\frac{\sum\nolimits_{p=1}^{N}{{{\left( {{\upsilon }_{z,p}}-{{{\bar{\upsilon }}}_{z}} \right)}^{2}}}}{N}}$.其中，${{{\bar{\upsilon }}}_{x}}{{{\bar{\upsilon }}}_{y}}{{{\bar{\upsilon }}}_{z}}$分别为x、y和z方向上颗粒群的平均速度，p为颗粒的标识，N为颗粒的总数.得到的脉动速度与平均速度具有同样的量纲.

从图 7可以看出，颗粒群x、y方向脉动自始自终基本保持一致，x、y方向同性.最初颗粒之间没碰撞，x、y、z值一致，各向同性；之后颗粒相互作用，z值逐渐大于x、y方向值，表明此时颗粒之间碰撞剧烈，混合剧烈，混乱程度高；碰撞之后，颗粒群系统慢慢归于均匀，脉动速度值下降，慢慢接近x、y方向值，但仍高于x、y方向值.

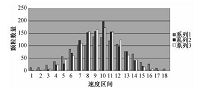
图 8显示的是4.9 s时颗粒群系统的速度分布图，其中1为小于v_i－2(i为x、y、z)的速度区间，18代表的是大于v_i+2的速度区间，2到17分别代表的是(v_i－2，v_i+2)区间内以0.25cm/s为间隔的16个均分小区间.系列1为z方向，系列2为x方向，系列3为y方向，可以发现，3个方向速度都呈现大多数颗粒速度降落在中间区域，拥有较大速度或较小速度的颗粒都处于少数，大致呈现类似于高斯分布的规律，此时也说明颗粒呈现出均匀混合的理想气体速度特性，从另一侧面说明本文模拟的颗粒群系统处于一个稳定状态.

3.2 三维多颗粒沉降位置及统计量分析

为考察颗粒群中颗粒分布不均匀性，本文选择用统计学中的变异系数来描述.这里简单介绍一下变异系数,这是用来描述离散程度的统计学量.变异系数定义为$C\upsilon \text{=}\frac{\sqrt{\sum\nolimits_{i=1}^{{{N}_{s}}}{{{\left( {{n}_{i}}-\bar{n} \right)}^{2}}/{{N}_{s}}}}}{{\bar{n}}}$.式中，n_i为第i个子区域内的颗粒数目(以颗粒中心点所在子区域为准)，N_s为子区域的数目，n-为子区域内的平均颗粒数目.变异系数可以用来表示颗粒分布的非均匀性，其值越大则表示非均匀性越强，值为0时表示在子区域划分的分辨率下分布完全均匀.

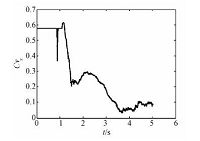
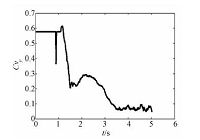
图 9和图 10显示x、y方向变异系数随时间的变化规律，可以发现x、y方向走势基本一致，这也说明x、y方向同性.在1s之后由于颗粒的相互作用，诸如DKT过程的影响，颗粒开始向x、y方向运动，填补初始情况下边界周边的空地，从而减小了非均匀性，之后由于颗粒群的互相碰撞等强烈相互作用，使得颗粒系统逐渐混合均匀，趋向于理想原子运动状态，故而非均匀性进一步减小，x、y变异系数值进一步减少.

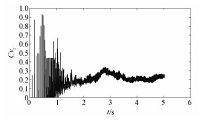
图 11显示z方向的变异系数随时间的变化关系，初始阶段的上下突变为较多颗粒同时穿越分割线造成，并无多大实际意义，由大体趋势可以知道，刚开始颗粒y向速度相差不大，故相对位置变化不大，Cv值变化不大，之后由于颗粒的相互作用，碰撞，导致速度差异，从而导致位置差异，即导致Cv上升，之后大致稳定在0.2左右.

3.3 三维多颗粒沉降颗粒流场相互作用分析

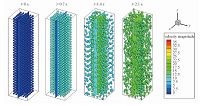
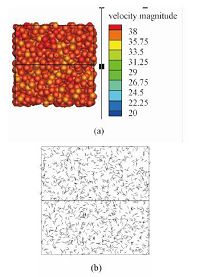
图 12显示不同时刻颗粒群的运动位置、速度和中间截面流体速度，黑色箭头代表速度矢量，圆球颜色代表各自的绝对速度，标度尺显示在图 13(a)的右下部分.t=0s时，颗粒群和流体均处于静止状态.之后颗粒开始运动，逐渐影响中间流场截面，t=0.7s时，中间截面只受部分周围颗粒对它的影响，形成规律的一条条竖纹.之后颗粒群继续发生强烈的相互作用，越来越多的颗粒进入中间截面，进而影响中间截面的流动状况，t=1.4s时有部分颗粒已近乎与中间流场速度保持一致.t=2.1s时，颗粒群内已不再像1.4 s时还存在大量不等速度颗粒，中间截面也是类似情况.颗粒群与流体之间的速度差异也越来越小，从图上来看，可以大致认为t=2.1s时系统已处于速度空间的稳定状态.之后颗粒之间由于相互碰撞，进一步在位置空间达到稳定，使整个颗粒群系统中颗粒具有类似于理想原子的运动规律，表现为均匀而又混沌的状态，如图 13所示.

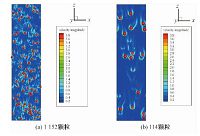
图 14(a)和图 14(b)分别给出1152颗粒和114颗粒稳定后某一时刻的涡量图，其中144颗粒算例初始情况除计算区域和各方向上颗粒数目缩短为1152颗粒的一半外，其余均无变化.从图中可看出，颗粒周围都出现较大的涡量值，与Wang^[8]结果吻合.还可看出，在同样初始体积分数下，1000数量级颗粒群更容易出现大量颗粒群的团聚行为，虽然100数量级的颗粒群也捕捉到了颗粒的DKT现象和颗粒群的聚集行为，但聚集规模不大，多为3、4个颗粒.并且随着颗粒数目的增加，颗粒之间碰撞更易发生，对周围流场的扰动更频繁，颗粒对远处的影响远比少颗粒数目情况下弱，流场上呈现更多的是紊乱的不规则的尾涡，颗粒之间发生强烈的相互作用.

4 结论

本文采用LB-EBF方法对三维悬浮颗粒群进行全解析直接数值模拟，最多模拟1152颗粒(1000数量级)，对三维颗粒群的沉降过程及其与流场的相互作用进行分析，结果表明：

1) 颗粒群x、y方向脉动自始自终基本保持一致，x、y方向同性.最初较短时间内各向同性，之后颗粒相互作用，z值大于x、y方向值.

2) 颗粒群系统处于稳定状态时，速度分布大致呈现类似于高斯分布的规律，中间多，两头少，颗粒呈现出均匀混合的理想气体速度特性.

3) x、y方向变异系数走势基本一致，x、y方向同性，Cv_x、Cv_y经历先减少后增大再减小的过程.Cv_z大致经历先增大再振荡的过程.

4) 1000数量级比100数量级颗粒群更容易出现大量颗粒群的团聚行为，颗粒对远处的影响远比少颗粒数目情况下弱，流场上呈现更多的是紊乱的不规则的尾涡.