随着全球经济的发展和城市化建设的加快,气溶胶颗粒物污染已经成为当今国内外关注的焦点,大气气溶胶会造成空气质量下降,影响生态环境,给人体健康带来较大危害.当前,人们对大气气溶胶污染还不能实现实时准确的预测和有效的治理,主要原因在于对气溶胶微观动力学演化过程的认识还很缺乏,气溶胶的微观动力学演化过程包括核化、凝结/蒸发和聚并.其中,核化在大气气溶胶的生长演化过程中扮演最基本的角色,即发生物质的相变过程.水蒸气的核化过程是大气环境中较为常见的自然现象,由于水蒸气的均相核化需要较大的过饱和度而较难发生,不能用来解释实际大气环境中的核化现象.研究发现,大气环境中存在的离子对核化过程有重要影响[1].因此研究离子诱导水蒸气核化问题有重要的理论和应用价值.
以往对于核化过程的研究主要基于理论推导和实验研究,而经典核化理论[2]以及随后出现的多种修正理论模型[3-4]对核化过程的预测和实验结果相比有较大差距.主要因为传统的理论分析方法不能对分子团簇形成过程的微观信息进行准确描述.近年来,随着计算机技术的快速发展,分子动力学方法正逐渐成为研究微观物理问题的重要工具,以往基于分子动力学方法对核化过程的研究多集中在均相和异相核化过程的研究[5-9],对离子诱导水蒸气核化过程的研究较少[10].本文采用分子动力学模拟方法对水蒸气均相核化过程和离子诱导水蒸气核化过程进行模拟,利用模拟结果分析核化速率、临界团簇尺寸和团簇的微观结构特征,对比不同带电量离子对核化过程的影响.
1 分子动力学模拟模拟系统是一个边长为50.4nm的立方体盒子.对于每种工况,体系中包含10000个均匀分布的水分子.在离子诱导核化过程中,体系中加入40个钠离子,为对比不同带电量的离子对核化过程的影响,用虚拟离子Na2+代表环境中普遍存在的正二价离子.
任意2个粒子间的相互作用势能包括Lennard-Jones 12-6势能和静电势能.势函数表达式
| ${U_{ij}} = 4{\varepsilon _{ij}}\left[ {{{\left( {{{{\sigma _{ij}}} \over {{r_{ij}}}}} \right)}^{12}} - {{\left( {{{{\sigma _{ij}}} \over {{r_{ij}}}}} \right)}^6}} \right] + {{{q_i}{q_j}} \over {{r_{ij}}}},$ | (1) |
下标i和j分别代表第i和j个粒子,q为粒子的带电量,r为粒子间的距离,σ和ε为粒子间LJ势能参数,分别表示离子间特征长度和单个粒子的能量,ε0为真空介电常数,各粒子的势能参数如表 1,不同粒子间的LJ势能参数采用式(2) 混合法则计算:
|
|
表 1 不同粒子势能参数 Table 1 Values of potential parameters |
| ${\sigma _{ij}} = ({\sigma _i} + {\sigma _j})/2,{\varepsilon _{ij}} = \sqrt {{\varepsilon _i}\cdot{\varepsilon _j}} .$ | (2) |
为减少计算量,同时考虑到粒子间作用力的相对大小,模拟过程中LJ势能和库伦势能的截断半径分别取1.0nm和5.0nm,水分子为SPC/E模型[11],键长和键角分别固定为rOH=1.0Å,θHOH=109.47°.体系采用周期性边界条件,Velocity Verlet算法[12]求解粒子运动方程.
模拟初始阶段,水分子为均匀分布,初始速度符合Maxwell-Boltzmann分布,模拟体系的初始温度为1000K.系统在Nose-Hoover热浴下经过100000步后达到平衡(设定为t=0ps).随后撤去热浴,采用速度标定法将系统的温度标定到380K,采用Nose-Hoover热浴将模拟体系的温度保持在380K,水蒸气过饱和度(本文中定义为体系中水蒸气的密度和对应温度下的饱和水蒸气密度之比)为S=3.512.研究表明,采用直接热浴法和载气带走热量法[5]对核化过程的影响差异很小且直接热浴法具有更高的计算效率[10],因此本文采用直接热浴法实现降温过程.本文中,初始温度的选择是为了保证初始时刻在有限的研究区域内有足够多分布均匀且不发生聚集的水分子.选择较高过饱和度是为了在模拟时间度内得到完整的成核过程.虽然温度和过饱和度的选择跟实际相差较大,但这不影响本文的关注重点,即水蒸气核化过程的微观信息.这种高温高过饱和的模拟方法被广泛应用到成核过程的模拟中[5, 8, 10].非平衡阶段的模拟时间为4ns,时间步长为2fs.
本文的模拟使用LAMMPS开源程序代码[13],为分析模拟过程核化信息(核化速率、临界团簇大小),每经过5ps统计一次颗粒的相关信息.当水分子中氧原子(或者离子与氧原子)间的距离小于3.5Å时,认为2个水分子(离子-水分子)连接在一起,且属于同一个分子团簇[14].
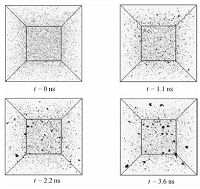
2 模拟结果分析 2.1 核化过程图 1为水蒸气均质核化过程中不同时刻体系核化过程快照.当t=0ns时体系处于温度为1000K的平衡状态,随着模拟体系温度的降低水蒸气分子逐渐开始核化,t=1.1ns时模拟盒子内出现一些由几个水分子凝聚在一起形成的小团簇,随着核化的进行,t=2.2ns时小团簇通过生长形成大团簇.当t=3.6ns时,系统达到核化和蒸发的动态平衡.
|
Download:
|
| 图 1 不同时刻水蒸气均相核化过程快照 Fig. 1 Snapshots of the homogeneous nucleation system at different t values | |
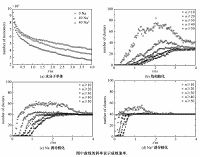
核化速率定义为单位时间单位体积内生成的活化核(尺寸大于临界团簇尺寸)个数.图 2(a)为游离水分子单体数目随时间变化图,图 2(b)—图 2(d)为采用5个不同的团簇尺寸阈值(10,20,30,40,50) 后,3种模拟工况下分子团簇数目随时间变化情况.由图 2(a)可看出,加入钠离子后,随着核化过程的进行,游离水分子单体数目减少速度加快,且加入正二价钠离子后,游离水分子单体数目减少速度更快.这说明离子的存在会加快水蒸气核化,且随着所加离子带电量的增加,核化加快.由图 2(b)—图 2(d)可看出,在3种模拟工况下,模拟过程均经历3个阶段:诱导阶段(无活化核产生)、稳定核化阶段(活化核以稳定的速率产生)、聚并阶段(分子团簇个数由于聚并而减少[15]),当加入离子后,前期诱导阶段变短,后期聚并现象更加明显.以均相核化为例,在核化过程第1和第2阶段,当阈值取10时,团簇数目增长较快,而当阈值取30~50时,水分子团簇数目增长的斜率基本相同,这表明,在模拟过程第1和第2阶段,尺寸大于10的分子团簇大量产生,但只有尺寸大于30的分子团簇才可以继续长大,由此可初步估算均相核化的临界团簇尺寸在10~30之间,且根据Yasuoka-Matsumoto分析法[5],模拟体系的核化速率均可以通过阈值为30~50时曲线上升部分拟合直线的斜率求得.同理可获得离子诱导核化的核化速率,结果如表 2.
|
Download:
|
| 图 2 模拟体系中单体和大于特定阈值的团簇数目随时间变化 Fig. 2 Temporal evolutions of the numbers of monomers and clusters larger than specific thresholds | |
|
|
表 2 模拟结果 Table 2 Simulation results |
从动力学角度分析,分子团簇在达到临界尺寸时生长和衰减达到平衡.团簇的生长和衰减率可根据团簇分析法获得[5]:分子团簇在间隔Δt(5ps)内大小由n变为n+k的概率β由式(3) 得出,式中Mn,n+k(t)表示在时间间隔Δt=5ps内,大小为n的团簇中生长/衰减为n+k(k=…,-2,-1,0,1,2,…)的个数.〈〉t表示在时间间隔Δt′内取平均.
| ${\beta _{n,n + k}} = {{{{\left\langle {{M_{n,n + k}}\left( t \right)} \right\rangle }_t}} \over {\sum\limits_{k = - \infty }^\infty {{M_{n,n + k}}{{\left. {\left( t \right)} \right\rangle }_t}} }}.$ | (3) |
分子团簇的平均生长率〈k〉+(n),平均衰减率〈k〉-(n)和平均变化速率〈k〉(n):
| ${\left\langle k \right\rangle _ + }\left( n \right) = \sum\limits_{k = 1}^\infty {k{\beta _{n,n + k}}} ,$ | (4) |
| ${\left\langle k \right\rangle _ - }\left( n \right) = \sum\limits_{k = - \infty }^{ - 1} {k{\beta _{n,n + k}}} ,$ | (5) |
| $\left\langle k \right\rangle \left( n \right) = {\left\langle k \right\rangle _ + }\left( n \right) + {\left\langle k \right\rangle _ - }\left( n \right).$ | (6) |
临界团簇满足条件
| $\left\langle k \right\rangle \left( n \right) = 0.$ | (7) |
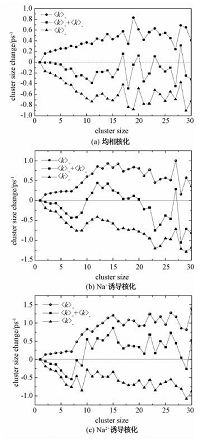
本文分别提取3种不同的模拟工况下稳定核化阶段相等时间间隔内颗粒信息(均相核化:t=1.5~1.8ns,Na+诱导核化: t=0.25~0.55ns,Na2+诱导核化: t=0.1~0.4ns)对分子团簇大小变化进行分析.分析结果如图 3,表 2列出3种工况下动力学临界团簇大小.由模拟结果可以看出,加入钠离子后,核化过程临界团簇尺寸减小,且正二价钠离子影响效果更加明显.
|
Download:
|
| 图 3 分子团簇大小变化分析 Fig. 3 Analysis of the cluster size change | |
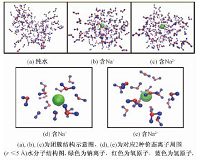
图 4(a)—图 4(c)为三种模拟工况分别达到平衡状态(t=3.6ns)时团簇的微观结构图(团簇大小均为154) ,图 4(d)、图 4(e)为图 4(b)、图 4(c)对应2种价态离子周围(r≤5 Å)水分子分布结构图,从图 4(a)、图 4(c)可发现团簇并非为球形,更接近于椭球形,不含离子的团簇中水分子排列没有明显的规律,而在含离子团簇中,离子处于团簇中心,周围水分子中的氧原子朝向离子,这是由于离子对氧原子的吸引作用.从图 4(d)、图 4(e)发现,由于正二价离子较正一价离子能产生更强的电场力,正二价离子周围水分子排列更紧密.
|
Download:
|
| 图 4 平衡状态(t=3.6ns)时水分子团簇示意图 Fig. 4 Snapshots of water cluster at the equilibrium point(t=3.6ns) | |
此外,体系中水分子团簇微观结构的平均信息可以用径向分布函数和配位数来描述,径向分布函数可以理解为区域密度和平均密度的比,配 位数表示距离目标离子r内某种粒子的个数.本文对3种模拟工况分别达到平衡状态(t=3.6ns)时水分子团簇微观结构进行分析比较,径向分布函数g(r)和配位数N(r)的对比如图 5,本文模拟结果和文献[16]结果相同,说明钠离子对周围水分子吸引力较水分子之间的吸引力强,据此可以对以上核化过程的差异进行解释:离子周围产生的电场导致离子存在时团簇的形成功减小,核化过程容易发生.此外,正二价离子比正一价离子周围产生的电场力大,因此核化过程更容易发生.

|
Download:
|
| 图 5 平衡状态(t=3.6ns)时水分子团簇径向分布函数(a)和配位数(b) Fig. 5 Radial distribution function (a) and coordination number (b) at the equilibrium point (t=3.6ns) | |
为验证本文结果的合理性,将均相核化过程模拟结果与经典核化理论(classical nucleation theory,CNT)[2]计算结果以及已有文献的模拟结果进行对比[17],对比结果如表 3.
|
|
表 3 MD模拟结果和CNT结果对比 Table 3 Comparison of MD simulation results with the CNT results |
从表 3可以看出,CNT预测结果中成核速率较MD模拟结果大,临界晶核尺寸较MD模拟值小.本文中的分子动力学模拟结果和CNT结果之间的差距和文献中的结果符合良好.这种差距的产生是已有核化过程分子动力学模拟研究结果的共性,主要是由于CNT不能准确描述核化过程中团簇的热力学参量随尺寸的变化情况.
3 结论本文采用分子动力学方法模拟水蒸气均相核化过程和离子诱导核化过程,采用团簇分析法分析大于不同阈值的团簇数随时间的变化情况,通过最小二乘法分别拟合获取3种模拟工况下的核化速率,从动力学角度分析临界团簇大小,对比不同带电量离子对核化过程的影响.此外,采用径向分布函数和配位数分析对比不同模拟体系达到平衡状态时水分子团簇的微观结构,解释3种工况下核化过程的差异.结果表明,钠离子对周围水分子的引力较水分子间的引力大,导致核化速率增大,临界团簇尺寸减小,核化过程更容易发生,且正二价离子比正一价离子对核化过程的影响更大.通过对核化过程的分子动力学模拟,有助于进一步探究复杂边界条件以及不同成分物质核化过程的微观机理,进而为更加准确的成核理论模型的建立提供参考.
| [1] | Loeb L, Kip A, Einarsson A. On the nature of ionic sign preference in CTR wilson cloud chamber condensation experiments[J]. The Journal of Chemical Physics , 1938, 6 (5) :264–273. DOI:10.1063/1.1750242 |
| [2] | Laaksonen A, Talanquer V, Oxtoby D W. Nucleation: measurements, theory, and atmospheric applications[J]. Annual Review of Physical Chemistry , 1995, 46 (1) :489–524. DOI:10.1146/annurev.pc.46.100195.002421 |
| [3] | Dillmann A, Meier G. A refined droplet approach to the problem of homogeneous nucleation from the vapor phase[J]. Journal of Chemical Physics , 1991, 94 (5) :3872–3884. DOI:10.1063/1.460663 |
| [4] | Hale B N. Application of a scaled homogeneous nucleation-rate formalism to experimental data at TTC[J]. Physical Review A , 1986, 33 (6) :4156–4163. DOI:10.1103/PhysRevA.33.4156 |
| [5] | Yasuoka K, Matsumoto M. Molecular dynamics of homogeneous nucleation in the vapor phase. I. Lennard-Jones fluid[J]. Journal of Chemical Physics , 1998, 109 (19) :8451–8462. DOI:10.1063/1.477509 |
| [6] | Suh D, Yasuoka K. Nanoparticle growth analysis by molecular dynamics: spherical seed[J]. The Journal of Physical Chemistry B , 2011, 115 (36) :10631–10645. DOI:10.1021/jp201964h |
| [7] | 宋粉红, 刘朝, 刘娟芳, 等. 水蒸气在纳米固体颗粒上异质核化的分子动力学研究[J]. 工程热物理学报 , 2013, 34 (10) :5. |
| [8] | Yasuoka K, Matsumoto M. Molecular dynamics of homogeneous nucleation in the vapor phase. Ii. water[J]. Journal of Chemical Physics , 1998, 109 (19) :8463–8470. DOI:10.1063/1.477510 |
| [9] | 张相雄, 陈民. 杂质颗粒湿润性对非均相形核的影响[J]. 工程热物理学报 , 2012, 33 (10) :1774–1776. |
| [10] | Pérez A, Rubio A. A molecular dynamics study of water nucleation using the Tip4p/2005 model[J]. The Journal of Chemical Physics , 2011, 135 (24) :244505. DOI:10.1063/1.3672063 |
| [11] | Chowdhuri S, Chandra A. Molecular dynamics simulations of aqueous NaCl and KCl solutions: Effects of ion concentration on the single-particle, pair, and collective dynamical properties of ions and water molecules[J]. Journal of Chemical Physics , 2001, 115 (8) :3732–3741. DOI:10.1063/1.1387447 |
| [12] | Paterlini M G, Ferguson D M. Constant temperature simulations using the langevin equation with velocity verlet integration[J]. Chemical Physics , 1998, 236 (1) :243–252. |
| [13] | Plimpton S. Fast parallel algorithms for short-range molecular dynamics[J]. Journal of Computational Physics , 1995, 117 (1) :1–19. DOI:10.1006/jcph.1995.1039 |
| [14] | Caleman C, van der Spoel D. Evaporation from water clusters containing singly charged ions[J]. Physical Chemistry Chemical Physics , 2007, 9 (37) :5105–5111. DOI:10.1039/b706243e |
| [15] | Suh D, Yoon W, Shibahara M, et al. Molecular dynamics analysis of multiple site growth and coalescence effects on homogeneous and heterogeneous nucleations[J]. Journal of Chemical Physics , 2008, 128 (15) :154523. DOI:10.1063/1.2904459 |
| [16] | Brodskaya E, Lyubartsev A P, Laaksonen A. Molecular dynamics simulations of water clusters with ions at atmospheric Conditions[J]. Journal of Chemical Physics , 2002, 116 (18) :7879–7892. DOI:10.1063/1.1467893 |
| [17] | Matsubara H, Koishi T, Ebisuzaki T, et al. Extended study of molecular dynamics simulation of homogeneous vapor-liquid nucleation of water[J]. Journal of Chemical Physics , 2007, 127 (21) :214507. DOI:10.1063/1.2803899 |
 2016, Vol. 33
2016, Vol. 33 


