2. 中国科学院大学, 北京 100049 ;
3. 东方锅炉股份有限公司, 四川 自贡 643000
2. University of Chinese Academy of Sciences, Beijing 100049, China ;
3. Dongfang Boiler Group Co. LTD, Zigong 643000, Sichuan, China
循环流化床燃煤发电技术在燃料适用性和污染物排放等方面具有明显的优势.为进一步提高供电效率、降低污染物的排放,发展大型化和超临界是当前循环流化床技术的主要发展方向之一[1-3].在循环流化床锅炉大型化的过程中,大尺寸炉膛的结构设计和多旋风气固分离系统优化布置是保证炉膛内部物料流动分布均匀性以及高效气固分离的关键技术,是循环流化床锅炉开发和设计的重要内容[4-6].
对于超临界循环流化床锅炉,传统的单炉膛结构会由于炉膛横截面尺寸太大,出现二次风的穿透能力不足问题.为解决上述问题,多家科研单位的超临界循环流化床锅炉设计方案采用“裤衩腿”型双布风板炉膛结构[7-9],该结构有效地解决了二次风穿透问题,但对炉膛两腿参数控制有较高的要求,控制不当会出现“翻床”现象,导致两侧流动状态严重偏离,影响锅炉运行的经济性和安全性[10-11].
吕清刚等[12]在多年基础研究和工程实践的基础上,提出超临界循环流化床环形炉膛设计方案.该炉型的炉膛截面是由内、外两圈壁面围成的环形结构,可以从理论上有效地解决二次风穿透问题,并且内、外环壁面的设计也为更多的受热面提供了空间,存在取消外置式换热器的可能性.
作为一个全新的炉型结构,环形炉膛内气固流动特性的掌握对该炉型的设计放大和应用推广具有重要意义.为此,中国科学院工程热物理研究所搭建了一个环形炉膛六分离器循环流化床冷态实验台.本文以该实验台为研究对象,采用CPFD方法对环形炉膛内的气固流场进行数值模拟,分析炉膛的气固流动特性以及炉膛出口气固流动不均匀性,研究结果可为环形炉膛的设计提供有价值的信息.
1 数值计算方法CPFD方法采用欧拉-拉格朗日法耦合求解流体和颗粒的三维运动,流体基于Navier-Stokes方程,采用大涡模拟方法求解,颗粒相用MP-PIC (multiphase particle-in-cell)[13-14]数值方法来计算,并通过相间曳力与流体相耦合.MP-PIC 方法最早由Andrews和Drourke[13]及Snider[14]等提出,该方法最鲜明的特点是能够在三维空间内耦合求解颗粒和流体的动量方程.在CPFD计算中,每一个计算颗粒受到三维外力的作用,如流体曳力、重力、静-动摩擦力和颗粒碰撞和其他外力.所用到的数值计算颗粒并不是物理意义上的颗粒,而是由一定数量的具有相同性质(成分、尺寸、密度和温度等)的颗粒组成的“颗粒团”或者“颗粒簇”.气相和颗粒的运动是通过独立的控制方程来计算的,由于两相流动近似为等温且气相视为不可压缩,在N-S方程组中不需要考虑能量方程.对于气相,控制方程为
| ${\partial \over {\partial t}}({\rho _g}{\theta _g}) + \nabla \cdot({\rho _g}{\theta _g}{v_g}) = {S_g},$ | (1) |
| $\eqalign{ & {\partial \over {\partial t}}({\rho _g}{\theta _g}{v_g}) + \nabla \cdot({\rho _g}{\theta _g}{v_g}{v_g}) = \cr & - \nabla P + \nabla \cdot{\theta _g}{\tau _g} + {\rho _g}{\theta _g}g - F, \cr} $ | (2) |
式中,θg为气体体积分数,ρg和νg分别为气相的密度和速度,Sg为气体源项,P为气体压力,τg为气体应力张量,g为重力加速度,F是单位体积相间动量交换率,即颗粒和流体之间的粘性作用力:
| $F = \smallint \smallint fm\left( {{D_p}({v_g} - {v_p}) - {{\nabla P} \over {{\rho _P}}}} \right)dmdv,$ | (3) |
式中,Dp为曳力系数,νp为颗粒速度,ρp是颗粒密度,f是概率分布函数.其中,相间曳力函数Dp由下式给出:
| ${D_p} = 4.5{{{\mu _g}} \over {{\rho _p}r_p^2}}{f_b},$ | (4) |
式中,μg为气体动力粘度,rp为颗粒半径,系数fb由曳力模型给出.本文采用的曳力模型是由Wen-Yu模型和Ergun模型线性变换而成的Wen-Yu/Ergun模型:
| ${f_b} = {f_w},{\theta _p} < 0.75{\theta _{cp}},$ | (5) |
| $\eqalign{ & {f_b} = {f_w} + {{{\theta _p} - 0.75{\theta _{cp}}} \over {0.1{\theta _{cp}}}}({f_e} - {f_w}), \cr & 0.75{\theta _{cp}} \le {\theta _p} \le 0.85{\theta _{cp}}, \cr} $ | (6) |
| ${f_b} = {f_e},{\theta _p} > 0.85{\theta _{cp}},$ | (7) |
式中,θcp为颗粒紧密堆积时的体积分数,fw和fe分别由Wen-Yu模型和Ergun模型获得.
颗粒间碰撞利用颗粒法向应力模型:
| ${\tau _p} = {{{P_s}\theta _p^\gamma } \over {{\rm{max}}[({\theta _{cp}} - {\theta _p}),\varepsilon (1 - {\theta _p})]}},$ | (8) |
式中,Ps是一个正的常数,默认值为1.2≤γ≤5为模型的自有参数,ε是一个为消除模型中奇异点而构造的数量级为10-7的小量.
2 计算对象的建立本文数值模拟的几何模型按照大型循环流化床环形炉膛冷态实验台的实际尺寸建立.实验系统本体由环形炉膛、6个并联布置的旋风分离器和返料器组成,结构示意图见图 1(a).炉膛由外环壁面和内环壁面相套构成,外环壁面横截面尺寸为1.68m×1m,内环壁面横截面尺寸为1.1m×0.42m,流通截面积为1.18m2,布风板以上炉膛高度为8.0m.旋风分离器为6个并联布置,返料器为一进二出型,炉膛底部外环壁面上布置12个返料口.

|
Download:
|
| 图 1 实验系统本体及简化的模型 Fig. 1 The whole model and the simplified model of the annular combustion chamber | |
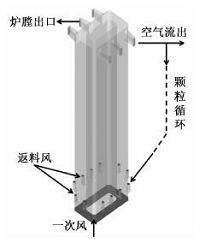
研究重点关注环形结构的炉膛内气固流动特性,因此对实验系统进行了简化(如图 1(b)),省去旋风分离器和返料系统.简化后的模型用自定义外部循环的方式实现炉膛内气固流动的三维非稳态数值模拟(见图 2).在每次迭代完成后计算炉膛各个出口颗粒的质量流率,并于下次迭代开始前将颗粒由返料口返还至炉膛.为保证炉膛内物料平衡,假设旋风分离器的分离效率为100%,即炉膛出口的颗粒全部送回至炉膛.
|
Download:
|
| 图 2 炉膛外部循环的实现 Fig. 2 Solids recirculation | |
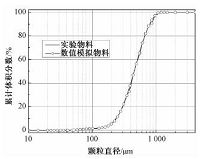
数值模拟的边界条件见表 1,表观风速为4.5m/s,模拟的静止料位高度为400mm.实验物料为石英砂,中位粒径453μm,真密度2600kg/m3,堆积密度1270kg/m3.数值模拟所用物料与实验物料具有相同的密度和粒径分布,颗粒粒径分布见图 3.
|
|
表 1 边界条件设置 Table 1 Boundary conditions |
|
Download:
|
| 图 3 物料粒径分布 Fig. 3 Particle size distribution | |
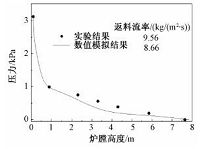
首先考察数值模拟结果的准确性,图 4将数值模拟得到的压力分布和返料流率的结果与实验结果进行对比.表明,数值模拟结果与实验结果吻合较好,因此数值模拟结果是可靠的,可以很好地反映环形炉膛内的气固流动特性.
|
Download:
|
| 图 4 数值模拟压力与实验压力轴向分布 Fig. 4 Pressure axial profiles predicted by simulation and obtained in the experiment | |
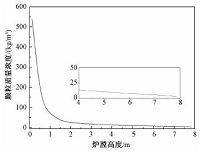
图 5给出环形炉膛内颗粒质量浓度分布曲线.由图可见,炉膛底部颗粒质量浓度最大,且随炉膛高度增加迅速减小,在布风板1.5m高度以上区域颗粒浓度低于50kg/m3.
|
Download:
|
| 图 5 颗粒质量浓度分布 Fig. 5 Axial distribution of solids concentration | |
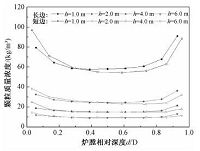
图 6给出不同炉膛高度上截面颗粒质量浓度径向分布,图中炉膛相对深度为0和1分别对应外环壁面和内环壁面.结果显示,颗粒质量浓度呈现壁面附近高而中心区域低的对称分布,且长短边的分布基本一致.王超[15]在“裤衩型”结构的循环流化床冷态实验台中的颗粒浓度径向分布结果与本文环形炉膛冷态实验台中的结果一致.
|
Download:
|
| 图 6 颗粒质量浓度径向分布 Fig. 6 Radial distribution of solids concentration | |
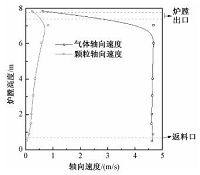
炉膛中气相速度与颗粒速度的偏差,即气固间滑移速度,对炉内气固流动有重要影响.图 7给出炉膛截面气体和颗粒轴向速度平均值沿炉膛高度的分布曲线.由图可见,炉膛截面上气体轴向速度平均值随炉膛高度增加基本不变,而颗粒轴向速度随炉膛高度增加而增大,最大值约0.8m/s.炉膛顶部空间,受炉膛出口结构的影响,气相、颗粒相的向上运动转变为炉膛出口方向的横向运动,因而轴向速度急剧减小.
|
Download:
|
| 图 7 炉膛截面气体和颗粒轴向速度平均值分布 Fig. 7 Gas and solids axial velocity distributions | |
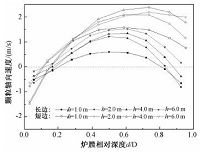
图 8给出不同炉膛高度上长边侧和短边侧的颗粒轴向速度分布曲线,速度为正值表明颗粒向上流动,负值表明颗粒向炉膛底部回流.整体上看,颗粒轴向速度呈壁面附近低而中心区域高的分布趋势,近壁区存在明显的颗粒回流.沿炉膛高度增加,中心区域颗粒向上速度增大,近壁区的颗粒回流逐渐减弱.
|
Download:
|
| 图 8 颗粒轴向速度径向分布 Fig. 8 Radial distribution of solids axial velocity | |
此外,长边侧的颗粒轴向速度基本成对称分布,且内、外环边壁附近都出现明显的颗粒回流;与长边侧的结果相比,短边侧的颗粒轴向速度在内环壁面附近更高,而在外环壁面附近更低.
长边侧的颗粒轴向速度径向分布曲线与“裤衩型”炉膛[15]中的一致,呈对称分布;而受环形炉膛这一复杂炉型结构的影响,短边侧的颗粒轴向速度分布特性与“裤衩型”炉膛[15]的结果存在一定的差异.
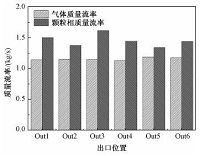
3.3 炉膛出口气固均匀性为研究炉膛并联各出口见气固流动分配的均匀性,图 9对比各个出口上气相和颗粒相的质量流率.通常情况下,炉膛出口气固质量流率的最大偏差不超过10%即可满足工业需求.
|
Download:
|
| 图 9 炉膛出口气固流率分布 Fig. 9 Profiles of gas and solids mass fluxes at combustion chamber outlets | |
从图 9可见,各出口气相流动分布均匀性很好,质量流率最大偏差值为0.06kg/s,最大偏差量仅为5.3%.颗粒相的质量流率差异较大,质量流率最大偏差值为0.28kg/s,最大偏差量为19.2%.
多分离器并联布置时产生的气固流动分配不均匀的现象一方面是由气固两相流动的多样性引起的,另一方面受炉膛结构及分离器布置形式的影响.因此,需要从调整炉膛结构及出口布置形式方面着手改善炉膛各出口间气固流动的均匀性.
4 结论本文针对环形炉膛六分离器循环流化床环形炉膛冷态实验台开展环形炉膛内气固流动特性的CPFD数值模拟研究,通过与实验所得压力分布和返料流率对比,得出数值模拟结果准确性较好,可用于研究环形炉膛内气固流动特性.
颗粒浓度主要集中在炉膛底部,并随炉膛高度的增加迅速衰减.炉膛高度1.5m以上区域颗粒浓度变化较小,低于50kg/m3.
在炉膛截面上,颗粒浓度呈现壁面附近高而中心区域低的分布趋势.而颗粒轴向速度的分布与颗粒浓度的相反,颗粒在炉膛中心区域向上流动,在壁面附近出现回流.
炉膛出口气固流动分配均匀性的研究显示,气相流动分布均匀性很好,最大偏差量仅为5.3%.颗粒相的质量流率差异较大,最大偏差量为19.2%.
| [1] | 吕俊复, 于龙, 张彦军, 等. 600MW超临界循环流化床锅炉[J]. 动力工程 , 2007, 27 (4) :497–501. |
| [2] | 吕清刚, 宋国良, 孙运凯, 等. 690t/h循环流化床锅炉设计特点与运行特性分析[J]. 动力工程学报 , 2010, 30 (12) :899–903. |
| [3] | 程乐鸣, 周星龙, 郑成航, 等. 大型循环流化床锅炉的发展[J]. 动力工程 , 2008, 28 (6) :817–826. |
| [4] | Hack H, Hotta A, Kettunen A, et al. Ultra-supercritical CFB technology to meet the challenge of climate change[R]. Foster Wheeler Energia Oy, Finland, 2008. |
| [5] | 廖磊, 那永杰, 吕清刚, 等. 六个旋风分离器并联布置循环流化床的实验研究[J]. 中国电机工程学报 , 2011, 31 (11) :11–16. |
| [6] | 周星龙, 程乐鸣, 张俊春, 等. 六回路循环流化床颗粒浓度及循环流率实验研究[J]. 中国电机工程学报 , 2012, 32 (5) :9–14. |
| [7] | 刘静, 王勤辉, 骆仲泱, 等. 600MWe超临界循环流化床锅炉的设计研究[J]. 动力工程 , 2003, 23 (1) :2179–2184. |
| [8] | 孙献斌. 超临界循环流化床锅炉的研发[J]. 热力发电 , 2008, 37 (1) :1–3. |
| [9] | 聂立, 王鹏, 彭雷, 等. 600 MW超临界循环流化床锅炉的设计[J]. 动力工程 , 2008, 28 (5) :701–706. |
| [10] | 孙纪宁, 王哲, 杨志伟, 等. 裤衩腿循环流化床流动特性及翻床机理的研究[J]. 动力工程学报 , 2010, 30 (5) :336–341. |
| [11] | 李金晶, 李燕, 刘树清, 等. 裤衩腿结构循环流化床锅炉床料不平衡现象的数值模拟[J]. 动力工程 , 2008, 28 (1) :28–32. |
| [12] | 吕清刚, 高鸣, 孙运凯, 等. 大型循环流化床锅炉[P]. 北京:CN102226518A,2011-10-26. |
| [13] | Andrews M J, Orourke P J. The multiphase particle-in-cell (MP-PIC) method for dense particulate flows[J]. International Journal of Multiphase Flow , 1996, 22 (2) :379–402. DOI:10.1016/0301-9322(95)00072-0 |
| [14] | Snider D M. An incompressible three-dimensional multiphase particle-in-cell model for dense particle flows[J]. Journal of Computational Physics , 2001, 170 (2) :523–549. DOI:10.1006/jcph.2001.6747 |
| [15] | 王超. 600 MW超临界CFB锅炉炉膛气固流动特性的数值模拟研究[D]. 杭州:浙江大学,2011. http://www.cnki.com.cn/article/cjfdtotal-ahdl201401003.htm |
 2016, Vol. 33
2016, Vol. 33 


