2. 中国科学院大学, 北京 100190 ;
3. 中国安全生产科学研究院, 北京 100012
2. University of Chinese Academy of Sciences, Beijing 100190, China ;
3. China Academy of Safety Science and Technology, Beijing 100012, China
合成孔径雷达(synthetic aperture radar,SAR)三维成像是一种新的SAR三维分辨成像技术,是在传统的SAR二维成像的基础上发展起来的,可以解决SAR二维成像中存在的叠掩、顶底倒置等几何失真问题[1-3],并获取SAR二维成像所无法获取的高程向分辨率,真实的还原观测目标的三维场景图.基于以上特点,目前SAR三维成像已广泛应用于山川、河谷及城市地区等复杂的观察场景中,在军事侦察、灾害预测、资源调查和地形融合等领域具有重要的应用价值和巨大的应用潜力[4].
常用的SAR三维成像算法主要有3大类:三维BP(Back Projection)算法、三维CS(Chirp Scaling)算法和三维RD(Range Doppler)算法[5],文献[5]中的三维CS算法及三维RD算法是在跨航向采用波束形成原理并分别结合二维CS算法及二维RD算法实现的.本文基于波束形成原理的SAR三维成像算法则,通过在航迹向-跨航向平面同时采用波束形成原理,以获取航迹向-跨航向这个平面的二维分辨率,在距离向采用脉冲压缩技术以获取距离向分辨率,即可获取观测目标的三维分辨率,实现观测目标的SAR三维成像.波束形成原理是通过阵列天线,接收来自空间不同方向的信号,并对其进行加权求和,以形成指向某个空间特定方向的波束,波束的主瓣对准目标信号,波束的零瓣对准噪声及干扰信号[5],使输出信号的信噪比有所提高,能准确确定点目标位置,并提高图像质量.
本文将波束形成原理用于SAR三维成像,分析了基于波束形成原理的SAR三维成像观测几何模型及波束形成原理在航迹向/跨航向上的运用模型;基于本文的模型及算法,仿真分析并验证了波束形成算法中距离近似所满足的条件;最后基于仿真实验数据,对点目标进行SAR三维成像并分析点目标成像质量,验证了本文算法的正确性及有效性.
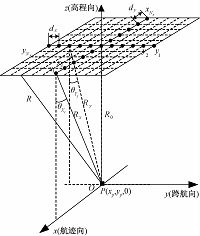
1 SAR三维成像观测几何模型及信号模型 1.1 SAR三维成像观测几何模型本文基于波束形成原理的SAR三维成像采用下视工作模式,其观测几何模型如图 1所示.图 1的x轴为航迹向、y轴为跨航向、z轴为高程向.在高为H且与航迹向-跨航向平面平行的平面 中,大小为Lx×Ly且具有Nx×Ny个阵元的面阵均匀分布在z轴四周各个网格顶点上.x、y方向的阵元间距分别为dx、dy,阵列长分别为Lx、Ly,故有Lx=(Nx-1)dx、Ly=(Ny-1)dy,且
| $\begin{align} & x\left( i \right)=\frac{{{L}_{x}}}{2}-\left( i-1 \right){{d}_{x}}(i=1,2,\ldots ,{{N}_{x}}), \\ & x\in \left( -\frac{{{L}_{x}}}{2},\frac{{{L}_{x}}}{2} \right), \\ \end{align}$ | (1) |
| $\begin{align} & y\left( j \right)=\frac{{{L}_{y}}}{2}-\left( j-1 \right){{d}_{y}}(j=1,2,\ldots ,{{N}_{y}}), \\ & y\in \left( -\frac{{{L}_{y}}}{2},\frac{{{L}_{y}}}{2} \right), \\ \end{align}$ | (2) |
|
Download:
|
| 图 1 基于波束形成原理的SAR三维成像观测几何模型 Fig. 1 3D SAR imaging observation geometry model based on beam-forming principle | |
均匀线阵在x、y方向的转动角分别为θxi、θyj,且θxi∈(-θx_max,θx_max),θyj∈(-θy_max,θy_max),θx_max和θy_max是线阵在x、y方向的最大观测角.
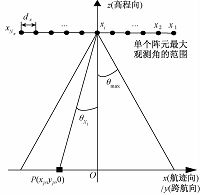
波束形成原理在航迹向/跨航向上的运用[5]如图 2所示,x/y方向的原点2侧均匀分布Nx/Ny个阵元,分别为x1/y1至xN/yN.分析x方向的阵元分布,单个阵元xi在x方向的转动角为θxi,表达式为
|
Download:
|
| 图 2 单个阵元照射观测目标的观测角范围 Fig. 2 The observation angle range of beaming the target with single array element | |
| ${{\theta }_{{{x}_{i}}}}=-{{\theta }_{x\_max}}+\frac{2{{\theta }_{x\_max}}\left( k-1 \right)}{K-1},k=1,2,\cdots ,K,$ | (3) |
其中,K是航迹向上的采样点数,不同的θxi决定阵列所形成波束的主瓣指向空间不同的方向,实现波束的主瓣对准目标信号,波束的零陷对准干扰及噪声,起到抑制干扰的作用.
假设R(xi,yj)是第(i,j)个阵元(xi,yj,H)与点目标P(xP,yP,0)的距离,则有
| $R({{x}_{i}},{{y}_{j}})=\sqrt{{{({{x}_{i}}-{{x}_{P}})}^{2}}+{{({{y}_{j}}-{{y}_{P}})}^{2}}+{{H}^{2}}},$ | (4) |
R(xi)是阵元(xi,yj,H)投影到x-z平面中的坐标(xi,0,H)与P(xP,yP,0)的距离,则有
| $R({{x}_{i}})=\sqrt{{{({{x}_{i}}-{{x}_{P}})}^{2}}+{{y}^{2}}_{P}+{{H}^{2}}};$ | (5) |
同理,R(yj)是阵元(xi,yj,H)投影到y-z平面中的坐标(0,yj,H)与P(xP,yP,0)的距离,则有
| $R({{y}_{j}})=\sqrt{{{x}^{2}}_{P}+{{({{y}_{j}}-{{y}_{P}})}^{2}}+{{H}^{2}}};$ | (6) |
R0是面阵中心(0,0,H)与P(xP,yP,0)距离,则有
| ${{R}_{0}}=\sqrt{{{x}^{2}}_{P}+{{y}^{2}}_{P}+{{H}^{2}}},$ | (7) |
其中,xP、yP、H均为常数.
1.2 SAR三维成像信号模型本文以步进频率连续波(SFCW)信号为例进行模型的分析和算法的推导.SFCW[6]是通过传感器运用频率调制系统产生一个脉冲序列,使每个脉冲具有单一的频率,其回波信号形式:
| $S(x,y,{{f}_{m}})=\sigma \left( P \right)exp[-j4\pi {{f}_{m}}R\left( x,y \right)/c]$ | (8) |
| ${{f}_{m}}={{f}_{0}}+m\Delta f$ | (9) |
其中,σ(P)是点目标P(xP,yP,0)的散射系数,fm是距离向信号频率的变化范围,f0是起始频率,Δ f是频率间隔,m=1,2,…,M是脉冲序列的第m个脉冲,M是脉冲序列的总脉冲个数,也即是距离向采样点数;c是波传播速度[6].
步进频信号由于距离向直接IFFT处理后便可完成距离向压缩,故对式(8)进行距离向IFFT处理,并且令σ(P)=1,则有
| $\begin{align} & s\left( x,y,n \right)=\sum\limits_{m=0}^{M-1}{S}(x,y,{{f}_{m}})exp\left( j\frac{2\pi }{M} \right)nm=exp\left[ -j\frac{4\pi {{f}_{c}}}{c}R\left( x,y \right) \right] \\ & sinc\left[ \pi M\left( \frac{n}{M} \right)-\frac{2\Delta fR\left( x,y \right)}{c} \right], \\ \end{align}$ | (10) |
式(10)实现了距离向压缩,获取了距离向分辨率.其中,2fc=2f0+(M-1)Δf,fc是中心频率.
2 波束形成算法波束形成算法是对阵列天线从空间不同方向接收到的信号进行加权求和,以形成指向某个特定方向的波束,加权求和时的权矢量决定波束的指向,进而决定了波束的主瓣对准目标信号,波束的零瓣对准噪声及干扰信号,提高成像质量.
实际应用中为防止严重的散焦,需满足由距离近似引起的相位变化不超过π/4[7],等效为由距离近似引起的距离变化不超过λ/16,即在满足近似距离R1与真实距离R之间的误差为|R1-R|≤λ/16的条件下,可对式(4)进行泰勒展开:
| $\begin{align} & R({{x}_{i}},{{y}_{j}})=R\left( 0,0 \right)+{{x}_{i}}\frac{\partial R}{\partial {{x}_{i}}}\left| _{{{y}_{j}}=0} \right.+{{y}_{j}}\frac{\partial R}{\partial {{y}_{i}}}\left| _{{{x}_{i}}=0} \right. \\ & ={{R}_{0}}+{{x}_{i}}\frac{({{x}_{i}}-{{x}_{P}})}{R({{x}_{i}},{{y}_{j}})}\left| _{{{y}_{j}}=0} \right.+{{y}_{j}}\frac{({{y}_{j}}-{{y}_{P}})}{R({{x}_{i}},{{y}_{j}})}\left| _{{{x}_{i}}=0} \right. \\ & ={{R}_{0}}+{{x}_{i}}\frac{{{x}_{i}}-{{x}_{P}}}{R({{x}_{i}})}+{{y}_{j}}\frac{{{y}_{j}}-{{y}_{P}}}{R({{y}_{j}})} \\ & ={{R}_{0}}+{{x}_{i}}sin({{\theta }_{{{x}_{i}}}})+{{y}_{j}}sin({{\theta }_{{{y}_{j}}}}). \\ \end{align}$ | (11) |
基于图 1观测几何模型,故每个阵元(xi,yj,H)与点目标P(xP,yP,0)的距离均有
| $R({{x}_{i}},{{y}_{j}})={{R}_{0}}+{{x}_{i}}sin({{\theta }_{{{x}_{i}}}})+{{y}_{j}}sin({{\theta }_{{{y}_{j}}}}),$ | (12) |
其中,R0是面阵中心与点目标P(xP,yP,0)的距离,θxi、θyj是单个阵元分别在x、y方向的转动角.式(12)体现出:每个阵元(xi,yj,H)与点目标P(xP,yP,0)间的距离R(xi,yj)不仅和阵元在x、y方向的位置有关,而且还和阵元在x、y方向的观测角有关,这正是波束形成算法的体现.
本文研究的算法是在距离向通过脉冲压缩技术获取距离向分辨率,在航迹向-跨航向平面同时使用波束形成原理获取航迹向-跨航向平面的二维分辨率.由于式(10)已经距离向压缩,故后续只需对其进行加权求和,将式(12)代入式(10)可得
| $\begin{align} & s\left( x,y,n \right)=exp\left( -j\frac{4\pi {{f}_{c}}}{c}{{R}_{0}} \right)exp\left\{ -j\frac{4\pi {{f}_{c}}}{c}[{{x}_{i}}sin({{\theta }_{{{x}_{i}}}})+{{y}_{j}}sin({{\theta }_{{{y}_{j}}}})] \right\} \\ & sinc\left[ \pi M\frac{n}{M}-\frac{2\Delta ~fR\left( x,y \right)}{c} \right]. \\ \end{align}$ | (13) |
针对式(13)的第2个相位表达式,选取相位因子:
| $w\left( i,j \right)=exp\left\{ +j\frac{4\pi {{f}_{c}}}{c}[{{x}_{i}}sin({{\theta }_{{{x}_{i}}}})+{{y}_{j}}sin({{\theta }_{{{y}_{j}}}})] \right\}.$ | (14) |
基于式(14)的相位因子,对式(13)加权求和:
| $\begin{align} & {{s}_{e}}\left( x,y,n \right)=\sum\limits_{j=1}^{N}{\sum\limits_{i=1}^{N}{w}}\left( i,j \right)s\left( i,j,n \right) \\ & \text{ }=\sum\limits_{j=1}^{N}{\sum\limits_{i=1}^{N}{\left\{ s\left( i,j,n \right)exp\left\{ j\frac{4\pi {{f}_{c}}}{c}[{{x}_{i}}sin({{\theta }_{{{x}_{i}}}})+{{y}_{j}}sin({{\theta }_{{{y}_{j}}}})] \right\} \right\}}}, \\ \end{align}$ | (15) |
即可获取航迹向-跨航向平面的二维分辨率.在分别获取距离向、航迹向和跨航向的分辨率后,便实现了对观测目标的SAR三维成像.
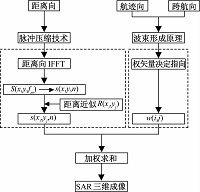
基于上述的算法分析,给出如图 3所示的算法流程图.
|
Download:
|
| 图 3 基于波束形成原理的SAR三维成像算法流程图 Fig. 3 Flow chart of 3D SAR imaging algorithm based on beam-forming principle | |
为验证本文算法的可行性及正确性,首先需验证距离近似条件:
| $\left| {{R}_{1}}-R\le \lambda /16 \right|.$ | (16) |
选取步进频频率fm∈(30,40)GHz,距离向采样点数Nr=201;x、y方向的阵元间距均为d=2 cm,阵列长L=2 m;航迹向和跨航向的观测角θxi、θyj∈(-π/60,π/60),航迹向和跨航向采样点数均为N=101,阵列在高程向的距离H=1 000 m,给出表 1所示的仿真参数.
|
|
表 1 仿真参数 Table 1 Simulation parameters |
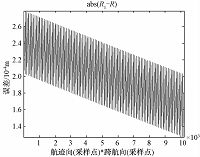
基于式(4)及式(12),分别求P(xP,yP,0)与各个阵元(xi,yj,H)的真实距离R和近似距离R1,然后比较误差|R1-R|与λ/16之间的大小,基于表 1参数得到图 4所示的误差图,由于真实距离与近似距离均是二维的,故图 4误差图的横坐标方向的采样点数为101×101个.
|
Download:
|
| 图 4 近似距离与真实距离的误差绝对值 Fig. 4 Absolute error in approximate distance | |
求出
基于上述算法分析及表 1仿真参数,对12个点目标:(15,15,0)、(15,-15,0)、(-15,15,0)、(-15,-15,0)、(15,15,30)、(15,-15,30)、(-15,15,30)、(-15,-15,30)、(15,15,60)、(15,-15,60)、(-15,15,60)、(-15,-15,60)进行成像.首先,对式(8)步进频信号的距离向进行IFFT处理,得到式(10)距离向压缩后的回波信号,经仿真验证式(16)距离近似条件成立后,则式(4)真实距离的表达式等效成式(12)近似距离的表达式;然后,将式(12)代入式(10)中得到式(13),针对式(13)的第2个相位选取式(14)的相位因子;最后,对式(13)加权求和即可实现波束形成原理在航迹向-跨航向平面的运用,从而获取航迹向-跨航向平面的二维分辨率,在获取距离向分辨率之后便实现了点目标的SAR三维成像.基于表 1参数,得到图 5所示的12个点目标SAR三维成像图.
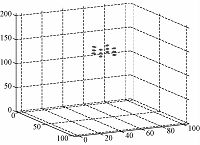
|
Download:
|
| 图 5 12个点目标SAR三维成像图 Fig. 5 3D SAR imaging of 12 point targets | |
为了更准确地验证图 5点目标的成像质量,需任取其中一个点目标P(15,15,0)进行进一步分析,得到图 6所示的单个点目标SAR三维成像图.为了验证图 6点目标的成像质量,则需分析图 6点目标在x-y平面、x-z平面及y-z平面的二维成像结果.由于图 6点目标在这3个平面二维成像图的相似度很高,故此处只列举出了图 7所示的点目标在x-y平面的二维成像图.图 7是图 6经过了16倍升采样,以点目标为中心、大小为<401×401>的在x-y平面的切片图.
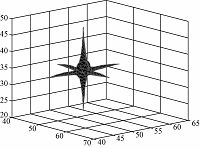
|
Download:
|
| 图 6 单个点目标SAR三维成像图 Fig. 6 3D SAR imaging of a single point target | |

|
Download:
|
| 图 7 点目标在x-y平面的二维成像图 Fig. 7 2D imaging of point target in the x-y plane | |
初步得出图 7成像结果正确,下一步还需分析图 7在x、y方向这二维的分辨率、峰值旁瓣比(PSLR)及积分旁瓣比(ISLR).
分别取出图 7在x、y方向的一维切片图像,得到图 8所示的航迹向、跨航向切片图像.

|
Download:
|
| 图 8 航迹向、跨航向切片图像 Fig. 8 Slice images in the azimuth and cross-track directions | |
同理,对图 6在x-z平面及y-z平面的二维成像图进行相同分析后,得到表 2所示成像质量指标的结果参数.主要包括点目标在距离向、航迹向及跨航向这3个方向的分辨率、PSLR以及ISLR的实际结果[8].
|
|
表 2 结果参数 Table 2 Result parameters |
分辨率的理论值在距离向、航迹向及跨航向分别为0.013、1.89和1.89 m;PSLR的理论值在距离向、航迹向及跨航向均为-13.2;ISLR的理论值在距离向、航迹向及跨航向分别为-10.4、-10.6和-10.6.通过比较各个成像指标的实际结果与理论结果,说明上述点目标图像质量的正确性,并很好验证了本文算法及模型的可行性及正确性.
4 结论本文研究了基于波束形成原理的SAR三维成像算法,结合该算法建立了SAR三维成像观测几何模型,以及波束形成原理在航迹向/跨航向上的运用模型,用以分析波束形成算法的原理;考虑波束形成算法中距离近似条件,并通过仿真验证了其正确性,进而验证了基于距离近似条件下的波束形成算法的正确性;最后通过仿真实验数据,验证了模型的准确性和本文成像算法的有效性及正确性.
| [1] | 杜磊. 阵列天线下视合成孔径雷达三维成像模型、方法与实验研究[D]. 北京:中国科学院电子学研究所, 2010. |
| [2] | 彭学明, 王彦平, 谭维贤, 等. 基于感兴趣区域搜寻的机载下视阵列3D+SAR波数域快速成像方法[J]. 电子与信息学报 , 2013, 35 (7) :1525–1531. |
| [3] | 杜磊, 王彦平, 洪文, 等. 机载下视三维成像合成孔径雷达空间分辨特性[J]. 测试技术学报 , 2010, 24 (2) :175–181. |
| [4] | 王斌, 王彦平, 洪文, 等. 线阵SAR三维成像分辨率分析[J]. 计算机仿真 , 2011, 28 (3) :282–286. |
| [5] | 张东浩. 线阵三维SAR成像算法研究及仿真[D].成都:电子科技大学, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10614-2009159998.htm |
| [6] | Yang J, Thompson J, Huang X, et al. Random-Frequency SAR imaging based on compressed sensing[J]. IEEE , 2013, 51 (2) :983–994. |
| [7] | 保铮, 邢孟道, 王彤. 雷达成像技术[M]. 北京: 电子工业出版社, 2004 : 177 -180. |
| [8] | 杨晓琳. 线阵成像雷达系统设计及幅相误差一致性校正方法研究[D]. 北京:中国科学院电子学研究所, 2014. http://www.cnki.com.cn/article/cjfdtotal-dzyx201311022.htm |
| [9] | 吴子斌, 朱宇涛, 粟毅, 等. 用于机载线阵三维SAR成像的MIMO阵列构型设计[J]. 电子与信息学报 , 2013, 35 (11) :2672–2677. |
| [10] | 韦顺军. 线阵三维合成孔径雷达稀疏成像技术 研究[D]. 成都:电子科技大学, 2013. http://www.cnki.com.cn/article/cjfdtotal-kxjs201408008.htm |
 2016, Vol. 33
2016, Vol. 33 


