边界元算法(boundary-element method,BEM)研究始于20世纪60年代. 1963年,Jaswon[1]和Symm[2]探讨位势问题的积分方程. 1967年,Rizzo[3]基于弹性静力学问题的边界积分方程,提出弹性静力学离散的边界积分方法. 1968年,Curse和Rizzo[4-5]研究求解弹性动力学方程的边界元算法. 1978年,Brbebia[6]总结工程中的边界元方法,建立起边界元方法的理论基础,确立了其在求解工程应用领域问题的地位,相关研究工作也迅速开展起来.
边界元算法是在经典的边界积分方程基础上,吸收有限元法相关技术的一种离散解析工具.这种方法利用控制方程的解析基本解(格林函数),建立相应的边界积分方程,然后再利用求积离散化技术来求解. 由于BEM只在边界上进行剖分和积分运算,可用有限的离散单元来准确地模拟边界,实际上是将问题进行了降维处理(如三维体积分变换为三维曲面积分),因而最终可获得较高的计算效率. 通过计算边界上的节点未知函数的离散解,然后根据实际应用的需求,有选择性地计算求解域内部未知函数值的半解析解,减少计算的盲目性,增加了计算的精确性. BEM的半解析性质,通常在保证边界积分解具有足够精度的情况下,能够获得较高的内部未知函数解的精度,大大增加了方法的适用范围,特别是对于处理无限域及半无限域问题、边界变量变化梯度较大的问题、多体绕流问题等[7-9].
基于面向地球动力学的边界元数值模拟软件(G3BEM)[10-11],本文将着重介绍求解斯托克斯流体力学方程的边界元算法,包括多种边界条件下的格林函数构造、边界积分方程、求解算法和误差理论分析,最后介绍其在板块俯冲动力学中的应用实例.
1 斯托克斯方程的格林函数 1.1 无限空间的格林函数对于给定不同边值条件的斯托克斯方程而言,若存在一系列的奇异解,使得空间中某个点或多个点处的速度和(或)压强的范数趋于无穷大,即本文所述的奇异性. 其中,最重要的奇异解是基于流体中某一位置x0处的点力源Fj, 由此引发的周围任意一点x处的速度ui和应力σij满足以下条件:
| ${{\partial }_{i}}{{\sigma }_{ij}}={{F}_{j}}\delta (x{{x}_{0}}),\partial {{}_{i}}{{u}_{i}}=0$ | (1) |
其中,x=(x1,x2,x3),x0=(x01,x02,x03),δ(x-x0)=δ(x1-x01)δ(x2-x02)δ(x3-x03),δ是Dirac-δ函数.对于无限空间流体而言,|x-x0|→∞的边界条件是ui→0以及σij→-P0δij, 其中P0是无限远处的压强,它与所研究的动力学问题不相关. 公式(1)的解可以写成以下形式:
| ${{u}_{i}}={{J}_{ij}}{{F}_{j}}/\eta ,{{\sigma }_{ik}}={{K}_{ijk}}{{F}_{}}$ | (2) |
其中,η是流体的黏滞系数. Jij和Kijk分别对应单位点力源的速度和应力格林函数. 把式(2)代入式(1),同时消去共有项Fj, 可以得到
| ${{\partial }_{i}}{{J}_{ij}}=0,{{}_{i}}{{K}_{ijk}}={{\delta }_{jk}}\delta (x{{x}_{0}}).$ | (3) |
式(3)可通过傅里叶变换或转换为泊松方程[12]进行求解,得到
| ${{J}_{ij}}\left( r \right)=\frac{1}{8\pi }\left( \frac{{{\delta }_{ij}}}{r}+\frac{{{r}_{i}}{{r}_{j}}}{{{r}^{3}}} \right),$ | (4) |
| ${{P}_{j}}\left( r \right)=\frac{3}{4\pi }\frac{{{r}_{j}}}{{{r}^{3}}},$ | (5) |
| ${{K}_{ijk}}\left( r \right)=\frac{1}{4\pi }\frac{{{r}_{i}}{{r}_{j}}{{r}_{k}}}{{{r}^{5}}}$ | (6) |
其中,r=x-x0,r=|r|. Jij,Pj和Kijk分别为 速度、压强和应力的格林函数. 从物理上讲,Jij代表x0位置处沿ej方向的点力源在x位置处所产生的速度的第i个分量.
1.2 一个自由滑动边界的格林函数如果空间中存在一个自由滑动的边界,x0位置处存在一个点力源,并且该位置距离边界的距离为d. 假设n是垂直于该边界并指向x0一侧的单位向量. 自由滑动边界可以等效的看作一个对称面,因此该边界对于流体的作用可以通过在x0的对称位置xIM0处增加一个对称的点力源而实现. 从而,该状态下的斯托克斯格林函数可以表示为
| $\begin{align} & {{G}_{ij}}(x-{{x}_{0}})={{{\hat{G}}}_{ij}}(x-{{x}_{0}})+G_{ij}^{IM}(x-x_{0}^{IM})= \\ & {{{\hat{G}}}_{ij}}(x-{{x}_{0}})+R_{pj}^{\left( 3 \right)}G_{ip}^{IM}(x-x_{0}^{IM}) \\ \end{align}$ | (7) |
其中,
| ${{R}^{\left( 3 \right)}}_{ij}=\left( \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \\ \end{matrix} \right).$ | (8) |
如果无限空间中存在一个刚性的固定边界,那么其斯托克斯格林函数为
| $\begin{align} & {{J}_{ij}}={{{\hat{J}}}_{ij}}+{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{J}}}_{ij}}, \\ & {{P}_{j}}={{{\hat{P}}}_{^{j}}}+{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{P}}}_{j}}, \\ & {{K}_{ijk}}={{{\hat{K}}}_{ijk}}+{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{K}}}_{ijk}}, \\ \end{align}$ | (9) |
其中,
| $\begin{align} & {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{J}}}_{ij}}=\frac{1}{8\pi }\left\{ \frac{{{\delta }_{ij}}}{R}-\frac{{{R}_{i}}{{R}_{j}}}{{{R}^{3}}}+2{{x}_{03}}{{\Delta }_{j}}\left[ {{x}_{03}}\left( \frac{{{\delta }_{ij}}}{{{R}^{3}}}-\frac{3{{R}_{i}}{{R}_{j}}}{{{R}^{5}}} \right)+\frac{{{\delta }_{i3}}}{{{R}^{3}}}{{R}_{j}} \right] \right. \\ & -\frac{1}{{{R}^{3}}}({{\delta }_{ij}}{{R}_{3}}+{{\delta }_{3j}}{{R}_{i}})+\left. \frac{3{{R}_{i}}{{R}_{j}}{{R}_{k}}}{{{R}^{5}}} \right\}, \\ \end{align}$ | (10) |
| ${{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P}}}_{j}}=\frac{1}{4\pi }-\left[ \frac{{{R}_{j}}}{{{R}^{3}}}-2{{x}_{03}}{{\Delta }_{j}}\left( \frac{{{\delta }_{3j}}}{{{R}^{3}}}-\frac{3{{R}_{j}}{{R}_{3}}}{{{R}^{5}}} \right) \right],$ | (11) |
| $\begin{align} & {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{K}}}_{ijk}}=-\frac{3}{4\pi }\left\{ -\frac{{{R}_{i}}{{R}_{j}}{{R}_{k}}}{{{R}^{5}}} \right.2{{x}_{03}}{{\Delta }_{j}}\left[ -\frac{{{x}_{03}}}{{{R}^{5}}} \right.{{\delta }_{ik}}{{R}_{j}}+\frac{{{x}_{3}}}{{{R}^{5}}}({{\delta }_{jk}}{{R}_{i}}+{{\delta }_{ij}}{{R}_{k}}) \\ & +\frac{{{R}_{i}}{{\delta }_{3j}}{{R}_{k}}}{{{R}^{5}}}\left. \left. \frac{{{R}_{i}}{{R}_{j}}{{R}_{k}}{{x}_{3}}}{{{R}^{7}}} \right] \right\} \\ \end{align}$ | (12) |
其中,r=(x1-x01,x2-x02,x3-x03),R=(x1-x01,x2-x02,x3+x03),r=[(x1-x01)2+(x2-x02)2+(x3-x03)2]½,R=[(x1-x01)2+(x2-x02)2+(x3+x03)2]½ .对于Δj,当j=1,2时,Δj=1; 当j=3时,Δj=-1.
1.4 两个平行的刚性边界的格林函数如果无限空间中存在2个平行的刚性边界,二者之间的距离为H, 且2个边界之间的x0(x01,x02,x03)位置处存在一个点力源,其距离一个边界的距离h=x03. 假设观测点的位置是x(x1,x2,x3), 那么r=(x1-x01,x2-x02,x3-x03), ρ=[(x1-x01)2+(x2-x02)2]½. 该边界条件控制下的格林函数可以通过傅里叶-贝塞尔积分[15]获得,其速度和压强的解包含两部分:
| ${{J}_{ij}}={{v}_{ij}}+{{w}_{ij}}$ | (13) |
| ${{P}_{j}}={{q}_{j}}+{{s}_{j}}$ | (14) |
其中,Jij, Pj分别是总的速度和压强格林函数. vij, qj分别是速度和压强格林函数的基本项,可以通过垂直于边界的无穷多个点力源阵列进行计算. 为了满足刚性边界上速度为零的边界条件,需要增加格林函数的补充项wij和sj.
1.4.1 速度和压强格林函数的基本项速度和压强的格林函数基本项可以通过下式表示:
| $\begin{align} & {{v}_{ij}}=\frac{1}{4\pi }\left[ {{\delta }_{ij}}{{\int }^{\infty }}_{0}{{J}_{0}}\left( \lambda \rho \right){{B}_{1}}\lambda d\lambda +{{\delta }_{i\alpha }}{{\delta }_{j\beta }}{{r}_{\alpha }}{{r}_{\beta }}\frac{1}{\rho } \right.{{\int }^{\infty }}_{0} \\ & \lambda {{J}_{1}}\lambda \rho {{B}_{2}}\lambda d\lambda {{\delta }_{i3}}{{\delta }_{j3}}{{\int }^{\infty }}_{0}\lambda {{J}_{0}}\lambda \rho {{B}_{3}}\lambda d\lambda +sgn \\ & \left( {{x}_{3}}h \right){{\delta }_{i3}}{{\delta }_{j\alpha }}+{{\delta }_{i\alpha }}{{\delta }_{j3}}{{r}_{\alpha }}{{\int }^{\infty }}_{0}\lambda {{J}_{0}}\lambda \rho {{B}_{4}}\lambda d\left. \lambda \right] \\ \end{align}$ | (15) |
| $\begin{align} & {{q}_{j}}=\frac{1}{2\pi }\left[ {{\delta }_{j\alpha }}{{r}_{\alpha }}\frac{1}{\rho } \right.{{\int }^{\infty }}_{0}\lambda {{J}_{1}}\lambda \rho {{B}_{1}}\lambda d\lambda +sgn\left( {{x}_{3}}h \right){{\delta }_{j3}} \\ & {{\int }^{\infty }}_{0}\lambda {{J}_{0}}\left( \lambda \rho \right){{B}_{4}}\lambda d\left. \left( \lambda \right) \right] \\ \end{align}$ | (16) |
其中,α,β=1,2, J0和J1分别是第一类贝塞尔函数的零阶和一阶项.
1) 当x3≥h时,满足
| $\begin{align} & {{B}_{1}}\left( \lambda \right)=\frac{sinh\lambda h}{sinh\lambda H}sinh\lambda (H{{x}_{3}}), \\ & {{B}_{2}}\left( \lambda \right)={{B}_{1}}\left( \lambda \right), \\ & {{B}_{3}}\left( \lambda \right)=\frac{d}{d\lambda }\left[ \frac{sinh\lambda h}{sinh\lambda H} \right.sinh\lambda (H{{x}_{3}}), \\ & {{B}_{4}}\left( \lambda \right)=\left. \frac{sinh\lambda h}{sinh\lambda H}cosh\lambda (H{{x}_{3}}) \right]. \\ \end{align}$ | (17) |
2) 当x3<h时,h需要替换为(H-h), x3替换为(H-x3), 可得
| $\begin{align} & {{B}_{1}}\left( \lambda \right)=\frac{sinh\lambda \left( Hh \right)}{sinh\lambda H}sinh\lambda {{x}_{3}}, \\ & {{B}_{2}}\left( \lambda \right)={{B}_{1}}\left( \lambda \right), \\ & {{B}_{3}}\left( \lambda \right)=\frac{d}{d\lambda }\left[ \frac{sinh\lambda \left( Hh \right)}{sinh\lambda H}sinh\lambda {{x}_{3}} \right], \\ & {{B}_{4}}\left( \lambda \right)=\frac{sinh\lambda \left( Hh \right)}{sinh\lambda H}cosh\lambda {{x}_{3}}. \\ \end{align}$ | (18) |
速度和压强的格林函数的补充项可以通过下面的方程组进行计算:
| $\begin{align} & {{w}_{\alpha \beta }}=\frac{1}{4\pi }\frac{\partial }{\partial {{r}_{\beta }}}\frac{{{r}_{\alpha }}}{\rho }{{\int }^{\infty }}_{0}\xi {{J}_{1}}\left( \rho \xi \right){{A}_{1}}\left( \xi \right)d\xi = \\ & -\frac{{{\delta }_{\alpha \beta }}}{4\pi }\frac{1}{\rho }{{\int }^{\infty }}_{0}\xi {{J}_{1}}\left( \rho \xi \right){{A}_{1}}\left( \xi \right)d\xi -\frac{{{r}_{\alpha }}{{r}_{\beta }}}{2\pi }\frac{1}{\partial {{\rho }^{2}}}\frac{1}{\rho }{{\int }^{\infty }}_{0}\xi {{J}_{1}}\left( \rho \xi \right){{A}_{1}}\left( \xi \right)d\xi \\ \end{align}$ | (19) |
其中,
| $\begin{align} & {{A}_{1}}\left( \xi \right)=\frac{1}{sin{{h}^{2}}\left( \xi H \right){{\left( \xi H \right)}^{2}}}\{\xi hH{{x}_{3}}sinh\xi \left( H{{x}_{3}} \right)sinh\xi \left( Hh \right)+ \\ & {{x}_{3}}[hsinh\xi Hcosh\xi (H-{{x}_{3}}-h)-Hsinh\xi hcosh\xi {{x}_{3}}]+ \\ & \xi H{{x}_{3}}sinh\xi Hcosh\xi (H{{x}_{3}})\frac{d}{d\xi }\left( \frac{sinh\xi \left( Hh \right)}{sinh\xi H} \right) \\ & Hsinh\xi {{x}_{3}}\left[ sinh\xi H\frac{d}{d\xi } \right]\left( \frac{sinh\xi h}{sinh\xi H} \right)+\xi H\frac{d}{d\xi }\left( \frac{sinh\xi \left( Hh \right)}{sinh\xi H} \right). \\ \end{align}$ | (20) |
| ${{w}_{33}}=\frac{1}{4\pi }{{\int }^{\infty }}_{0}{{J}_{0}}\left( \rho \xi \right){{A}_{2}}\xi d\xi .$ | (21) |
| $\begin{align} & {{A}_{2}}\left( \xi \right)=\frac{{{\xi }^{2}}}{sin{{h}^{2}}\left( \xi H \right){{\left( \xi H \right)}^{2}}}\{{{x}_{3}}[Hsinh\xi hcosh\xi {{x}_{3}}hsinh\xi Hcosh\xi \\ & (H{{x}_{3}}h)+\xi hHsinh\xi (H{{x}_{3}})sinh\xi \left( Hh \right)+\xi Hcosh\xi (H{{x}_{3}}) \\ & sinh\xi H\frac{d}{d\xi }\left( \frac{sinh\xi \left( Hh \right)}{sinh\xi H} \right)\xi {{H}^{2}}sinh\xi {{x}_{3}}\frac{d}{d\xi }\left( \frac{sinh\xi \left( Hh \right)}{sinh\xi H} \right)+ \\ & Hsinh\xi {{x}_{3}}sinh\xi H\frac{d}{d\xi }\left( \frac{sinh\xi h}{sinh\xi H} \right). \\ \end{align}$ | (22) |
| $\begin{align} & {{w}_{3\alpha }}{{_{(}}_{\alpha 3}}_{)}=-\frac{{{r}_{\alpha }}}{2\pi }\left[ \frac{\partial }{\partial {{\rho }^{2}}} \right.{{\int }^{\infty }}_{0}{{J}_{0}}\left( \rho \xi \right){{A}_{3}}\left( \xi \right)d\xi + \\ & \left. ({{\delta }_{i3}}{{\delta }_{j3}})\frac{\partial }{\partial {{\rho }^{2}}}{{\int }^{\infty }}_{0}{{J}_{0}}\left( \rho \xi \right){{A}_{4}}\left( \xi \right)d\xi \right] \\ \end{align}$ | (23) |
| $\begin{align} & {{A}_{3}}\xi =\frac{1}{sin{{h}^{2}}\left( \xi H \right)}\left[ hsinh\xi Hcosh\xi \right.(H{{x}_{3}}h)Hsinh\left( \xi h \right)cosh\left( \xi {{x}_{3}} \right)+ \\ & \frac{\xi }{sin{{h}^{2}}\xi h\xi {{H}^{2}}}\left\{ {{x}_{3}}\xi H \right.hsinh\xi {{x}_{3}}h+\frac{Hsinh\xi hsinh\xi \left( H-{{x}_{3}} \right)}{sinh\xi H} \\ & -\text{ }\frac{\xi h{{H}^{2}}sinh\xi {{x}_{3}}sinh\xi \left( Hh \right)}{sinh\xi H} \\ \end{align}$ | (24) |
其中,
| $\begin{align} & {{A}_{4}}\left( \xi \right)=\frac{\xi }{sin{{h}^{2}}\left( \xi H \right){{\left( \xi H \right)}^{2}}}-H\left( H-h \right)sinh\xi hsinh\xi {{x}_{3}}+ \\ & {{x}_{3}}hsinh\xi Hsinh\xi (H{{x}_{3}}h)+{{x}_{3}}Hsinh\xi hsinh\xi {{x}_{3}}] \\ \end{align}$ | (25) |
| ${{s}_{j}}=\frac{1}{2\pi }\left[ {{\delta }_{j\alpha }}{{r}_{\alpha }}\frac{1}{\rho }{{\int }^{\infty }}_{0}{{J}_{1}}\left( \rho \xi \right){{A}_{5}}\left( \xi \right)d\xi +{{\delta }_{j3}}{{\int }^{\infty }}_{0}{{J}_{0}}\left( \rho \xi \right){{A}_{6}}\left( \xi \right)d\xi \right].$ | (26) |
其中,
| $\begin{align} & {{A}_{5}}\left( \xi \right)=\frac{{{\xi }^{2}}}{sin{{h}^{2}}\left( \xi H \right){{\left( \xi H \right)}^{2}}} \\ & \left\{ sinh\xi Hsinh\xi (H{{x}_{3}})\left[ sinh\xi H\frac{d}{d\xi } \right. \right.\left( \frac{sinh\xi h}{sinh\xi H} \right)+ \\ & \xi H\frac{d}{d\xi }\left( \frac{sinh\xi \left( Hh \right)}{sinh\xi H} \right)+cosh\xi (H{{x}_{3}}) \\ & [\xi hHsinh\xi \left( Hh \right)+\left( Hh \right)sinh\xi hsinh\xi H]\}, \\ \end{align}$ | (27) |
| $\begin{align} & {{A}_{6}}\left( \xi \right)=\frac{{{\xi }^{2}}}{sin{{h}^{2}}\left( \xi H \right){{\left( \xi H \right)}^{2}}} \\ & \left\{ sinh\xi Hcosh\xi (H{{x}_{3}})\left[ sinh\xi H \right. \right.\frac{d}{d\xi }\left( \frac{sinh\xi h}{sinh\xi H} \right) \\ & \xi H\frac{d}{d\xi }\left( \frac{sinh\xi \left( Hh \right)}{sinh\xi H} \right)+sinh\xi (H{{x}_{3}}) \\ & [\xi hHsinh\xi \left( Hh \right)\left( Hh \right)sinh\xi hsinh\xi H]\}. \\ \end{align}$ | (28) |
基于速度和压强的格林函数,应力的格林函数可以进一步计算:
| ${{K}_{ijk}}={{P}_{j}}{{\delta }_{ik}}+\frac{\partial {{J}_{ij}}}{\partial {{x}_{k}}}+\frac{\partial {{J}_{kj}}}{\partial {{x}_{i}}}.$ | (29) |
该函数的不同项可以进行分组计算,主要包括以下6组: Kαβγ, Kαβ3, K3β3, Kα3γ, Kα33, K333, 其中,α,β,γ=1,2, 且α和γ是对称的.
| $\begin{align} & {{K}_{\alpha \beta \gamma }}=\frac{{{\delta }_{\alpha \gamma }}{{r}_{\beta }}}{2\pi }\left[ \frac{1}{\rho } \right.{{\int }^{\infty }}_{0}\lambda {{J}_{1}}\left( \lambda \rho \right){{B}_{2}}\left( \lambda \right)d\lambda \frac{1}{\rho }{{\int }^{\infty }}_{0}\lambda {{J}_{1}}\left( \lambda \rho \right){{B}_{1}}\left( \lambda \right)d\lambda \\ & \frac{1}{\rho }{{\int }^{\infty }}_{0}{{J}_{1}}\left( \xi \rho \right){{A}_{5}}\left( \xi \right)d\xi 2\frac{\partial }{\partial {{\rho }^{2}}}{{\int }^{\infty }}_{0}\xi {{J}_{1}}\left( \xi \rho \right){{A}_{1}}\left( \xi \right)\left. d\xi \right]\frac{{{\delta }_{\beta \gamma }}{{r}_{\alpha }}+{{\delta }_{\alpha \beta }}{{r}_{\gamma }}}{4\pi } \\ & \left[ \frac{1}{\rho } \right.{{\int }^{\infty }}_{0}\lambda {{J}_{1}}\left( \lambda \rho \right){{B}_{2}}\left( \lambda \right)d\lambda +2\frac{{{\partial }^{2}}}{{{\left( \partial {{\rho }^{2}} \right)}^{2}}}{{\int }^{\infty }}_{0}{{J}_{0}}\left( \lambda \rho \right){{B}_{1}}\left( \lambda \right)d\lambda \\ & 4\frac{\partial }{\partial {{\rho }^{2}}}\frac{1}{\rho }{{\int }^{\infty }}_{0}\xi {{J}_{1}}\xi \rho {{A}_{1}}\xi d\xi +{{r}_{\alpha }}{{r}_{\beta }}{{r}_{\gamma }}\pi \\ & \frac{\partial }{\partial {{\rho }^{2}}}\frac{1}{\rho }{{\int }^{\infty }}_{0}\lambda {{J}_{1}}\lambda \rho {{B}_{2}}\lambda d\lambda 2\frac{{{\partial }^{2}}}{{{(\partial {{\rho }^{2}})}^{2}}~}\left. \frac{1}{\rho }{{\int }^{\infty }}_{0}\xi {{J}_{1}}\left( \xi \rho \right){{A}_{1}}\left( \xi \right)d\xi \right] \\ \end{align}$ | (30) |
| $\begin{align} & {{K}_{\alpha \beta 3}}=\frac{{{\delta }_{\alpha \beta }}}{4\pi }\left[ \frac{\partial }{\partial {{x}_{3}}} \right.{{\int }^{\infty }}_{0}{{J}_{0}}\left( \lambda \rho \right){{B}_{1}}\left( \lambda \right)d\lambda \\ & \frac{\partial }{\partial {{x}_{3}}}\frac{1}{\rho }{{\int }^{\infty }}_{0}\xi {{J}_{1}}\left( \xi \rho \right){{A}_{1}}\left( \xi \right)d\xi +{{\int }^{\infty }}_{0}\lambda {{J}_{0}}\left( \lambda \rho \right){{B}_{4}}\left( \lambda \right)d\lambda \\ & -2\frac{\partial }{\partial {{\rho }^{2}}}{{\int }^{\infty }}_{0}{{J}_{0}}\left( \xi \rho \right)({{A}_{3}}\left( \xi \right)+{{A}_{4}}\left( \xi \right))d\xi \\ & +\frac{{{r}_{\alpha }}{{r}_{\beta }}}{4\pi }\frac{\partial }{\partial {{x}_{3}}}\frac{1}{\rho }{{\int }^{\infty }}_{0}\lambda {{J}_{1}}\left( \lambda \rho \right){{B}_{2}}\left( \lambda \right)d\lambda - \\ & 2\frac{\partial }{\partial {{x}_{3}}\partial {{\rho }^{2}}}\frac{1}{\rho }{{\int }^{\infty }}_{0}\xi {{J}_{1}}\left( \xi \rho \right){{A}_{1}}\left( \xi \right)d\xi + \\ & 2\frac{\partial }{\partial {{\rho }^{2}}}{{\int }^{\infty }}_{0}\lambda {{J}_{0}}\left( \lambda \rho \right){{B}_{4}}\left( \lambda \right)d\lambda 4\frac{{{\partial }^{2}}}{{{\left( \partial {{\rho }^{2}} \right)}^{2}}}{{\int }^{\infty }}_{0}{{J}_{0}}\left( \xi \rho \right) \\ & \left. ({{A}_{3}}\left( \xi \right)+{{A}_{4}}\left( \xi \right))d\xi \right] \\ \end{align}$ | (31) |
| $\begin{align} & {{K}_{3\beta 3}}=\frac{{{r}_{\beta }}}{2\pi }\left[ \frac{\partial }{\partial {{x}_{3}}} \right]{{\int }^{\infty }}_{0}\lambda {{J}_{0}}\left( \lambda \rho \right){{B}_{4}}\left( \lambda \right)d\lambda \\ & 2\frac{{{\partial }^{2}}}{\partial {{x}_{3}}{{\rho }^{2}}}{{\int }^{\infty }}_{0}{{J}_{0}}\left( \xi \rho \right)({{A}_{3}}\left( \xi \right)+{{A}_{4}}\left( \xi \right))d\xi \\ & \left. \frac{1}{\rho }{{\int }^{\infty }}_{0}\lambda {{J}_{1}}\left( \lambda \rho \right){{B}_{1}}\left( \lambda \right)d\lambda -1\rho {{\int }^{\infty }}_{0}{{J}_{1}}\left( \xi \rho \right){{A}_{5}}\left( \xi \right)d\xi \right] \\ \end{align}$ | (32) |
| $\begin{align} & {{K}_{\alpha 3\gamma }}=\frac{{{r}_{\alpha }}{{r}_{\gamma }}}{\pi }\left[ \frac{\partial }{\partial {{\rho }^{2}}} \right]{{\int }^{\infty }}_{0}\lambda {{J}_{0}}\left( \lambda \rho \right){{B}_{4}}\left( \lambda \right)d\lambda - \\ & \left. 2\frac{{{\partial }^{2}}}{{{\left( \partial {{\rho }^{2}} \right)}^{2}}}{{\int }^{\infty }}_{0}{{J}_{0}}\left( \xi \rho \right)({{A}_{3}}\left( \xi \right){{A}_{4}}\left( \xi \right))d\xi \right]+\frac{{{\delta }_{\alpha \gamma }}}{2\pi } \\ & [2\frac{\partial }{\partial {{\rho }^{2}}}{{\int }^{\infty }}_{0}{{J}_{0}}\left( \xi \rho \right)({{A}_{3}}\left( \xi \right){{A}_{4}}\left( \xi \right))d\xi {{\int }^{\infty }}_{0}{{J}_{0}}\left( \xi \rho \right){{A}_{6}}\left( \xi \right)d\xi ], \\ \end{align}$ | (33) |
| $\begin{align} & {{K}_{\alpha 33}}=\frac{{{r}_{\alpha }}}{4\pi }\frac{\partial }{\partial {{x}_{3}}}{{\int }^{\infty }}_{0}\lambda {{J}_{0}}\left( \lambda \rho \right){{B}_{4}}\left( \lambda \right)d\lambda + \\ & 2\frac{\partial }{\partial {{\rho }^{2}}}{{\int }^{\infty }}_{0}{{J}_{0}}\left( \xi \rho \right){{A}_{2}}\left( \xi \right)d\xi 2\frac{{{\partial }^{2}}}{\partial {{x}_{3}}\partial {{\rho }^{2}}}{{\int }^{\infty }}_{0}{{J}_{0}}\left( \xi \rho \right)({{A}_{3}}\left( \xi \right){{A}_{4}}\left( \xi \right))d\xi + \\ & 2\frac{\partial }{\partial {{\rho }^{2}}}{{\int }^{\infty }}_{0}{{J}_{0}}\left( \lambda \rho \right){{B}_{1}}\left( \lambda \right)d\lambda 2\frac{\partial }{\partial {{\rho }^{2}}}{{\int }^{\infty }}_{0}\lambda {{J}_{0}}\left( \lambda \rho \right){{B}_{3}}\left( \lambda \right)d\lambda , \\ \end{align}$ | (34) |
| $\begin{align} & {{K}_{333}}=\frac{1}{2\pi }-{{\int }^{\infty }}_{0}\lambda {{J}_{0}}\left( \lambda \rho \right){{B}_{4}}\left( \lambda \right)d\lambda - \\ & {{\int }^{\infty }}_{0}{{J}_{0}}\left( \xi \rho \right){{A}_{6}}\left( \xi \right)d\xi +\frac{\partial }{\partial {{x}_{3}}}{{\int }^{\infty }}_{0}{{J}_{0}}\left( \xi \rho \right){{A}_{2}}\left( \xi \right)d\xi + \\ & \left. \frac{\partial }{\partial {{x}_{3}}}{{\int }^{\infty }}_{0}{{J}_{0}}\left( \lambda \rho \right){{B}_{1}}\left( \lambda \right)d\lambda -\frac{\partial }{\partial {{x}_{3}}}{{\int }^{\infty }}_{0}\lambda {{J}_{0}}\left( \lambda \rho \right){{B}_{3}}\left( \lambda \right)d\lambda \right]. \\ \end{align}$ | (35) |
如前文所述,自由滑动边界条件等效于镜面的对称性. 因此,一个自由滑动加一个刚性的边界条件控制下的格林函数,可以通过对2个平行的刚性边界条件的格林函数进行转换而获得,方法是以2个平行刚性边界的中轴面为对称面,添加一个对称的点力源镜像点(类似于1.2节的方法). 从而,可获得一个自由滑动加一个刚性边界的格林函数:
| ${{G}_{ij}}(x{{x}_{0}})={{G}^{2w}}_{ij}(x{{x}_{0}})+{{G}^{IM}}_{ij}(x{{x}^{IM}}_{0})$ | (36) |
其中,G2wij是2个平行刚性边界的格林函数(见1.4节),GIMij是在镜像点xIM0=2Hn-x0位置处的点力源所对应的格林函数. H是自由活动和刚性边界之间的距离,或者说2个刚性边界之间距离的一半. n代表两个平行边界之间的单位垂直向量.
1.6 格林函数复杂项的预计算及数据库构建由前文可见,随着边界条件的增加,格林函数变得越来越复杂,因此数值计算也会越来越慢. 为了提高计算效率,可以对格林函数中的一些非常复杂的项进行预计算,并采用一定分辨率的网格系统,将预先计算好的数值做成一个数据库. 这样,在数值模拟的过程中,主程序将调用该数据库,并通过有限差分的插值处理后直接应用. 这种方法可以大大节省计算时间,因此G3BEM软件也采用了这种方法[10].
2 边界积分方程对于某种流体-Ⅱ (密度ρ2=ρ1+δρ, 黏滞系数η2=γη1)在另一种流体-Ⅰ (ρ1,η1)中由于重力的作用而产生的自发运动,其边界积分方程[16-17]为
| $\begin{align} & {{\chi }_{1}}({{x}_{0}}){{u}^{(1)}}_{j}({{x}_{0}})+\gamma {{\chi }_{2}}({{x}_{0}}){{u}^{(2)}}_{j}({{x}_{0}})= \\ & \frac{{{g}_{k}}\delta \rho }{{{\eta }_{1}}}\int x{{\prime }_{k}}{{J}_{ij}}(x{{x}_{0}}){{n}_{i}}\left( x \right)dS\left( x \right)+\left( 1\gamma \right) \\ & \int {{u}_{i}}\left( x \right){{K}_{ijk}}(x{{x}_{0}}){{n}_{k}}\left( x \right)dS\left( x \right) \\ \end{align}$ | (37) |
其中,x0是目标点,x是积分点. 积分符号是对2种流体的整个边界曲面进行积分. 假设S,V1和V2分别指示流体界面、流体-Ⅰ和流体-Ⅱ. 当x0点在S面上时,χ1(x0)=χ2(x0)=0.5; 当x0点在V1中时,χ1(x0)=1,χ2(x0)=0; 当x0点在V2中时,χ1(x0)=0,χ2(x0)=1. Jij(x-x0)和Kijk(x-x0)分别是速度和应力格林函数,γ代表 2种流体的黏滞系数比,γ=
当目标点x0在曲面S上时,u(1)j(x0)=u(2)j(x0)=uj(x0), 于是上述边界积分方程可简化为
| $\begin{align} & \frac{1}{2}\left( 1+\gamma \right){{u}_{j}}({{x}_{0}})= \\ & -\frac{{{g}_{k}}\delta \rho }{{{\eta }_{1}}}\int x{{\prime }_{k}}{{J}_{ij}}(x{{x}_{0}}){{n}_{i}}\left( x \right) \\ & dS\left( x \right)+\left( 1\gamma \right)\int {{u}_{i}}\left( x \right){{K}_{ijk}}(x{{x}_{0}}){{n}_{k}}\left( x \right)dS\left( x \right). \\ \end{align}$ | (38) |
我们首先对边界方程进行无量纲化,长度通过流体-Ⅱ的空间尺度(h)进行无量纲化处理,速度通过斯托克斯自由沉降速度Vs=g·Δρ·h2/η1进行处理,时间通过h/Vs进行无量纲化. 当x→x0时所产生的斯托克斯奇异解,通过标准的奇异解消除法[12]进行处理,就可以得到无量纲化的边界积分方程:
| $\begin{align} & {{u}_{j}}({{x}_{0}})={{P}_{j}}({{x}_{0}})+{{Q}_{j}}({{x}_{0}}),{{P}_{j}}({{x}_{0}})= \\ & \int (z{{z}_{0}}){{J}_{ij}}(x{{x}_{0}}){{n}_{i}}\left( x \right)dS\left( x \right), \\ & {{Q}_{j}}({{x}_{0}})=\left( 1\gamma \right)\int [{{u}_{i}}\left( x \right){{u}_{i}}({{x}_{0}})]{{K}_{ijk}}(x{{x}_{0}}){{n}_{k}}\left( x \right)dS\left( x \right) \\ \end{align}$ | (39) |
其中,Pj(x0)和Qj(x0)分别代表速度和应力格林函数的积分.
2.2 目标点在流体V1或V2中通过前一部分的公式计算得到边界曲面上的速度场后,可以据此对流体V1和V2中的任意位置的速度场等进行直接求解. 当x0点在V2中时,χ1(x0)=0,χ2(x0)=1. 边界积分方程可以转化为
| $\begin{align} & {{u}_{j}}({{x}_{0}})={{P}_{j}}({{x}_{0}})+{{Q}_{j}}({{x}_{0}}),{{P}_{j}}({{x}_{0}})= \\ & 1\gamma \int (z{{z}_{0}}){{J}_{ij}}(x{{x}_{0}}){{n}_{i}}\left( x \right)dS\left( x \right),{{Q}_{j}}({{x}_{0}})= \\ & 1\gamma \gamma \int {{u}_{i}}\left( x \right){{K}_{ijk}}(x{{x}_{0}}){{n}_{k}}\left( x \right)dS\left( x \right). \\ \end{align}$ | (40) |
相似的情况,当x0点在V1中时,χ1(x0)=1,χ2(x0)=0, 从而也很容易得到其边界积分方程.
3 方程求解及误差分析对于上述边界积分方程离散化后所形成的满秩矩阵的线性方程组的求解,可采用前人的一些标准方法,例如双共轭梯度法[7]、GMRES[18]方法等,在此不做叙述.
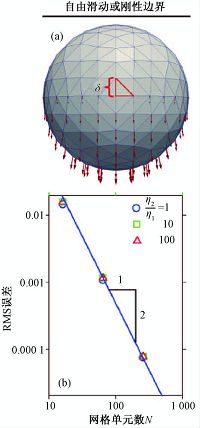
为了对边界元算法的求解误差进行分析,首先得到3组简单模型的解析解: 1)无限空间球形流体的运动模型[19];2)球形流体垂直于一个自由滑动边界的运动模型[20]; 以及3)球形流体垂直于一个刚性边界的运动模型[20]. 然后基于这3组解析解对边界元模型进行误差分析. 结果表明,边界元算法求得的速度场误差(RMS)随网格数(N)的增加而快速减小,即
|
Download:
|
| 图 1 (a)球体表面的曲面三角形网格化;(b)误差与网格单元数的关系 Fig. 1 (a) Surface discretization of a sphere using curved triangles; (b) dependence of the RMS error on the number of cells | |
基于前文所述的边界元算法,开发了一套三维地球动力学数值模拟软件(G3BEM). 该程序既可用于模拟大尺度的俯冲动力学、地幔形变等[10],又可用于计算微尺度的地幔矿物晶格优选定向及合成地震剪切波分裂等[11].
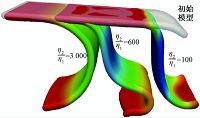
自然界中的大洋俯冲模式具有多样性,因此可以采用G3BEM软件对俯冲模式的选择进行了定量化的数值模拟. 如图 2所示,随着俯冲板块与周围地幔的黏滞系数的变化
|
Download:
|
| 图 2 板块俯冲模式依赖于板块与周围地幔的黏滞系数比值 Fig. 2 Dependence of subduction modes on the viscosity ratio between plate and surrounding mantle | |
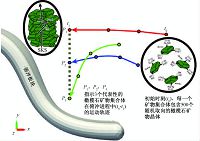
伴随俯冲进程,俯冲板块周围的地幔物质将发生复杂的运动和变形. 因此,我们可以采用示踪轨迹的方法,对俯冲板块任意时刻(如图 2所示的状态)的地幔中选取一系列规则排列的示踪点,通过斯托克斯流动的可逆性,反推其在初始时刻的位置. 然后可以正演模型,计算俯冲过程中这些示踪点所经历的有限应变演化. 同时,可以假设每个示踪点包含500个橄榄石矿物晶体,并对俯冲过程中这些矿物的晶格优选定向特征进行定量化的模拟. 最后,可以在地表设置一系列地震台站,假设当有剪切波从模型底部入射时,就可以合成其所生成的剪切波分裂特征,即快波偏振方向和快慢波的延迟时间(图 3).
|
Download:
|
| 图 3 俯冲带地幔流动、物质变形及地震波各向异性的数值模拟原理示意图 Fig. 3 Numerical modeling methods for subduction-induced mantel flow,material deformation,and seismic anisotropy | |
基于这部分算法,经过数值模拟得到,即使是在比较复杂的俯冲构造环境下,地幔有限应变椭球(FSE)亦可近似的作为地幔橄榄石晶格优选定向(CPO)的指示,并且FSE的长轴与CPO的a轴基本吻合,FSE的短轴与CPO的b轴基本吻合[11].但是,FSE和CPO的方向与地幔运动的速度方向并不总是保持一致,这意味着由俯冲带地震波各向异性的观测数据推测其下的地幔流动场需要特别小心.同时,从数值模型中可以识别出俯冲板块之下的地幔中2个变形特征截然不同的区域:一是上部的'简单剪切区’,该区域的各向异性特征产生垂直于海沟的快波方向;二是下部(直至410km)的'纯剪切区’,将产生平行于海沟的快波方向. 从而,地表观测到的剪切波分裂特征取决于二者之间的竞争关系. 进而,还发现板下地幔总的地震波各向异性特征受控于板块水平前进和海沟后撤距离之间的比值,当该比值<1时,快波方向平行于海沟; 反之,快波方向垂直于海沟.
5 小结边界元算法非常适合于求解无限或半无限空间的问题,其计算效率高并且收敛性也非常好. 但是当处理相对复杂边界问题时,由于其格林函数比较复杂,因此计算效率会大打折扣. 在这种情况下,一般采用对格林函数中不容易收敛的项进行预计算并建立相应的数据库,数值模拟进程中只需要调用数据库中的相关值并进行一定的插值即可,从而可以在不影响计算精度的条件下提高计算速度. 同时,边界元算法的第1步求解过程,一般只涉及对物质边界进行网格剖分,并在其相应节点上进行求解,因此可以简化研究问题的维度,从而大大提高计算效率. 而第2步可以有选择性的对其他任意位置处的点进行直接求解,这样就减少了计算的盲目性. 边界元算法的数值模拟,可以对板块俯冲动力学及俯冲带的地幔流动和地震波各向异性特征等进行细致的研究,也可以在其他地球动力学过程中得到很好的应用.
感谢石耀霖、刘勉、张怀、张理论、葛腾青、刘明启及Neil Ribe等的有益讨论和帮助.
| [1] | Jaswon M A. Integral equation methods in potential theory, Part 1[J]. Proceedings of the Royal Society of London Series A , 1963, 275 :23–32. DOI:10.1098/rspa.1963.0152 |
| [2] | Symm G T. Integral equation methods in potential theory, Part 2[J]. Proceedings of Royal Society of London Series A , 1963, 275 :33–46. DOI:10.1098/rspa.1963.0153 |
| [3] | Rizzo F J. An integral equation approach to boundary value problems of classical elastostatics[J]. Quarterly of Applied Mathematics , 1967, 25 :83–95. |
| [4] | Cruse T A, Rizzo F J. A direct formulation and numerical solution of the general transient elastodynamic problem, part 1[J]. Journal of Mathematical Analysis and Applications , 1968, 22 (1) :244–259. DOI:10.1016/0022-247X(68)90171-6 |
| [5] | Cruse T A, Rizzo F J. A direct formulation and numerical solution of the general transient elastodynamic problem, Part 2[J]. Journal of Mathematical Analysis and Applications , 1968, 22 (2) :341–355. DOI:10.1016/0022-247X(68)90177-7 |
| [6] | Brebbia C A. The boundary element method for engineers[M]. London: Pentech Press, 1978 : 189 . |
| [7] | Pozrikidis C. A practical guide to boundary element methods with the software library BEMLIB[M]. Boca Raton: CRC Press, 2002 : 440 . |
| [8] | Rjasanow S, Steinbach O. The fast solution of boundary integral equations[M]. New York: Springer US, 2007 : 284 . |
| [9] | Liu Y. Fast multipole boundary element method-Theory and applications in engineering[M]. Cambridge: Cambridge University Press, 2009 : 254 . |
| [10] | Li Z H, Ribe N M. Dynamics of free subduction from 3-D boundary-element modeling[J]. Journal of Geophysical Research: Solid Earth , 2012, 117 . |
| [11] | Li Z H, Di Leo J F, Ribe N M. Subduction-induced mantle flow, finite strain and seismic anisotropy: Numerical modeling[J]. Journal of Geophysical Research: Solid Earth , 2014, 119 :5052–5076. DOI:10.1002/2014JB010996 |
| [12] | Pozrikidis C. Boundary integral and singularity methods for linearized viscous flow[M]. New York: Cambridge University Press, 1992 : 259 . |
| [13] | Blake J R. A note on the image system for a stokeslet in a no-slip boundary[J]. Mathematical Proceedings of the Cambridge Philosophical Society , 1971, 70 :303–310. DOI:10.1017/S0305004100049902 |
| [14] | Ascoli E P, Dandy D S, Leal L G. Buoyancy-driven motion of a deformable drop toward a planar wall at low Reynolds number[J]. Journal of Fluid Mechanics , 1990, 213 :287–311. DOI:10.1017/S0022112090002336 |
| [15] | Liron N, Mochon S. Stokes flow for a stokeslet between two parallel flat plates[J]. Journal of Engineering Mathematics , 1976, 10 :287–303. DOI:10.1007/BF01535565 |
| [16] | Pozrikidis C. The deformation of a liquid drop moving normal to a plane wall[J]. Journal of Fluid Mechanics , 1990, 215 :331–363. DOI:10.1017/S0022112090002671 |
| [17] | Manga M, Stone H A. Buoyancy-driven interaction between two deformable viscous drops[J]. Journal of Fluid Mechanics , 1993, 256 :647–683. DOI:10.1017/S0022112093002915 |
| [18] | Fraysse V, Giraud L, Gratton S, et al. A set of GMRES routines for real and complex arithmetics on high performance computers . CERFACS Technical Report TR/PA/03/3, 2001: 20. http://cn.bing.com/academic/profile?id=2080710049&encoded=0&v=paper_preview&mkt=zh-cn |
| [19] | Batchelor G K. An introduction to fluid dynamics[M]. New York: Cambridge University Press, 1967 : 615 . |
| [20] | Brenner H. The slow motion of a sphere through a viscous fluid towards a plane surface[J]. Chemical Engineering Science , 1961, 16 :242–251. DOI:10.1016/0009-2509(61)80035-3 |
 2016, Vol. 33
2016, Vol. 33 


