月球作为距离地球最近的天体,一直都是人类努力探索的对象.对月球的探索是我们迈向更遥远宇宙的第一步.航天技术的发展使得可以对月球进行近距离观测,20世纪六七十年代掀起了探测月球的高潮,尤其是美国的阿波罗计划,带回了大量的数据和岩石样品等以供研究。1969年阿波罗11号在月面上设置了6台月震仪进行观测,其中4台正常工作[1].从1969到1977年,一共记录到约12000例月震,其中约7000例为深源月震[2],这些深源月震发生在约700~1100km深度范围,且许多深震丛集出现,并有着显著的周期行为[3],周期为27.2或27.5天[4],与地球-月球轨道几何参数有关[5],也与震源所在位置有关[6].我们知道,月球绕地球运行恒星月的时间为27.3天,而且月球总以一面对着地球,所以在月球的参考系中,地球与太阳的运行都是以月为周期.这种具有相同周期的行为预示着深源月震的发生与地球、太阳的作用很可能有某种关联,而潮汐作用正是引起月球内部应力场变化从而诱发月震的可能因素之一.由于太阳距离遥远,其潮汐作用与地球相比很小,所以主要考虑地球的潮汐作用对月球的影响.本文将对此进行一些定量的讨论.
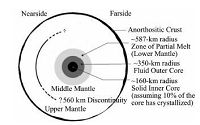
1 月球结构虽然长久以来人们对月球作了大量的研究工作,但是我们所掌握的资料仍然十分匮乏,对于月球内部结构的了解远不如对地球了解得详细.在研究地球结构时人们使用地震波数据反演的方法,这种方法在用来研究月球时有很大困难.首先,在月球表面不能像在地球上一样建设很多台站,这样就使得月震数据的覆盖面很小,难以做出全球模型的反演;其次,在1100km深度以下没有月震数据,此深度以下的月球结构无法用月震数据得出,只能通过与地球等行星的类比,利用重力、电磁等方法进行推测[7].人们通过多种地球物理方法得出的一个月球结构模型如图 1所示.
|
Download:
|
| 图 1 月球内部结构示意图[2] Fig. 1 Structure of the Moon | |
图 1表明,月球像地球一样也具有圈层结构,大体可分月壳、月幔、月核3个圈层,然而月球结构的一些细节仍然不能确定,比如是否存在液态核以及下月幔底部是否熔融,至今仍无定论.对于月球内部结构的了解不足也是对月球进行数值模拟的一大困难,因为要进行模拟就必须要有物理模型,要有准确的物理模型就必须要对其结构有准确的信息.虽然有这个困难,但是我们可以根据已有的知识,先根据合理的假设得出一个物理模型,然后依照此模型进行数值模拟,将得出的结果与实际观测对照,反过来检验我们所用模型的合理性.
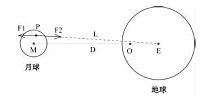
2 潮汐作用如图 2所示,假设2个天体(图中为月球与地球)绕它们共同的质心O作圆周运动,而它们各自作平动(即没有自转),那么对于其中一个天体上的参考点P,会受到万有引力F2和惯性离心力F1,它们的合力就是所谓的潮汐力.以月球球心为原点,月球球心到地球球心连线为x轴,则潮汐力在3个方向分量分别为:
| $\begin{align} & {{f}_{x}}=\frac{GMm}{{{L}^{2}}}\frac{D-x}{L}-\frac{GMm}{{{D}^{2}}}, \\ & {{f}_{y}}=-\frac{GMm}{{{L}^{2}}}\frac{y}{L}, \\ & {{f}_{z}}=-\frac{GMm}{{{L}^{2}}}\frac{z}{L}, \\ \end{align}$ |
其中,G为万有引力常数,M、m分别表示地球、参考单元质量,L、D分别表示参考单元、月球球心到地球球心的距离,x、y、z表示参考单元坐标.从上面公式可以看出,潮汐力大小与对面天体的质量成正比,与两天体之间距离的3次方成反比,太阳质量1.99×1030kg,是地球的3.3×106倍,而太阳到地球的距离1.5×108km,是月地距离的约400倍,计算可知月球受到太阳的潮汐作用大约为地球潮汐作用的0.6%.因此一般认为潮汐作用相对于地球的潮汐作用可以忽略不计.
|
Download:
|
| 图 2 地月系统潮汐作用示意图 Fig. 2 Tidal force of the Earth-Moon systerm | |
本文采用朱桂芝等[8]、陈绍林等[9]发展的一种方法生成网格.传统的经纬度划分网格方法会使球心处的网格过分密集,浪费计算资源.而本文所用的方法是先构造一个小立方体,在立方体6个面方向分别向外扩展,在扩展过程中可以将网格适当加密,将最后得到的大立方体投影成球体.
在本文计算过程中,使用上述方法将月球划分为1010223个单元,共1029984个节点,在表面处的单元边长约8km(约0.27°).剖面如图 3所示.

|
Download:
|
| 图 3 计算网格剖面图 Fig. 3 Profile of our working mesh | |
本文采用基于MPI环境的并行有限元计算.假设月球各层为均匀各向同性线弹性介质,使用泊松比为0.4999的弹性介质近似代表液态介质,分别计算了两个模型.两个模型使用相同的网格.材料参数的设置,对于1100km深度以上的部分,根据参考文献[10-12]中利用月震数据反演得到速度结构,我们依照月震波速计算出杨氏模量和泊松比;对于1100km深度以下部分则依照参考文献[2, 13-15]中的一些模型做出假设.
模型1:
分为月壳、上月幔、下月幔、月核4个均匀层,各层材料参数设置见表 1.
|
|
表 1 模型1的材料参数 Table 1 Material parameters in model 1 |
图 4(a)、图 4(b)给出潮汐作用引起月球表面的位移场计算结果.由于地球质量比月球质量大很多,月球受到的潮汐作用也比地球受到的作用更大,这在月球表面位移可以看出来,地球表面由于潮汐作用引起的位移大约为30cm.

|
Download:
|
| 图 4 潮汐作用下月球的位移场 Fig. 4 Tidal displacement on the Moon | |
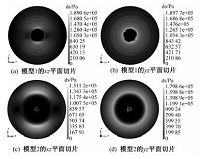
为了与月震的观测联系起来,有必要计算出最大剪应力的分布情况,图 5(a)、图 5(b)为计算出的最大剪应力的剖面图.
|
Download:
|
| 图 5 潮汐作用下最大剪应力剖面图 Fig. 5 Profiles of the maximal shear stresses | |
计算结果表明,当存在一个液态核的时候,最大剪应力将在最靠近液态核的外侧集中,亦即此处岩石容易发生断裂而造成月震.在此模型中,最大剪应力集中分布在紧靠液态核外侧的下月幔底部,即1300km深处.而此处已经处于1100km深度以下的无月震区域.如果下月幔底部也处于熔融状态,那么这个应力集中区应该会向外扩展到月震频发区,这就是模型2的内容.
模型2:
材料参数仍然按照速度结构(1100km深度以上)和假设得出,虽然还是核、幔、壳的结构,但在每个结构中又按照速度结构进行不同程度的细分,并假设下月幔底部处于熔融状态(泊松比设为0.4999).材料参数如表 2.表 3为各个不同圈层的对应半径.
|
|
表 2 模型2的材料参数 Table 2 Material parameters in model 2 |
|
|
表 3 模型2的各个圈层 Table 3 Moon structure in model 2 |
图 4(c)、图 4(d)给出潮汐作用引起的月球表面的位移场.图 5(c)、图 5(d)为最大剪应力的分布,对比模型1的结果可以看出,月球内部结构的改变对计算结果有影响.模型2的计算结果表明,当下月幔底部处于熔融状态时,最大剪应力的集中区域会扩展至下月幔底部附近,紧靠着熔融部分的一层之中,这样就与月震频发区的深度相吻合.由于中心网格较稀疏,所以有不规则的形状出现.
5 潮汐应力在一个近点月内的变化由于月球总将一面对着地球,如果月球绕地球是圆形的轨道,则虽然月球受到地球的潮汐作用,但潮汐应力的大小基本不会变化.然而,月球绕地球的轨道为椭圆形,它到地球的距离在一个近点月内(月球两次通过椭圆轨道近地点的时间)周期性变化.月球绕地球旋转的轨道椭圆偏心率为0.0549[16],在近地点和远地点距离地球相差10.4%.而潮汐力的大小和二天体间距离的3次方近似成反比,因此,在一个近点月周期内,估算出差应力相对和绝对变化量为28.1%,0.5 × 105Pa.可以看出在一个近点月的周期(27.554551d)之内,潮汐作用产生的差应力变化明显,这说明潮汐作用使岩石应力状态改变.实际观测到某些丛集的月震具有27.58d的周期[5],说明潮汐作用触发月震是很有可能的.实际观测到的另一些丛集的月震具有27.19 d的周期[5],这与交点月(即月球回到其轨道平面与黄道交点所需的时间)长度27.212220d相近,对某些纬度的月震可能这种纬向位置变化引起的应力作用更为明显.
太阳在一个月之内离月球最近和最远时距离相差0.51%,一个月内应力相对和绝对变化分别为1.5%、965 Pa.无论从太阳对月球的潮汐作用自身,还是与地球对月球的作用相比,太阳对月球的潮汐作用的月变化都很小,就潮汐作用来说,地球对月球始终起主导作用.
6 讨论和结论虽然计算的地球对月球的潮汐应力表明,潮汐应力可能是造成月震周期性的主要原因,但是,为什么会发生月震仍然存在未解的谜团.我们知道,通常岩石破裂遵循库仑-摩尔破裂准则,即在τ-σn平面上为τ=τ0+μσn的一条直线,当岩石所处的应力状态所表示的莫尔圆与之相切时,则岩石发生破裂.因此,对于处于一定应力临近破坏状态下的岩石,如果潮汐应力变化使其莫尔圆与岩石破裂线之间位置发生相对变化,可能会触发月震.
然而,1000km深度的月岩会处于什么样的应力状态呢?利用模型2假设的密度,可以计算出在月震多发区的静岩压力:
| $\frac{dp}{dr}=-\rho g,$ |
| $g=\frac{GM}{{{r}^{2}}},$ |
其中p表示在半径为r处的静岩压力,g为此处的重力加速度,M为半径小于r的球体部分的质量,G为万有引力常数.
整理上两式并积分可得:
| ${{P}_{i}}=\frac{GC{{\rho }_{i}}}{r}-\frac{2}{3}\pi G{{\rho }_{i}}^{2}{{r}^{2}}+{{A}_{i}},\text{ }2\le i\le 34,$ |
| ${{P}_{1}}=-\frac{2}{3}\pi G{{\rho }_{1}}^{2}{{r}^{2}}+{{A}_{1}},$ |
其中
| $C=-\frac{4}{3}\pi {{r}^{3}}_{i-1}{{\rho }_{i}}+\sum\limits_{j=1}^{i-1}{\frac{4}{3}\pi }({{r}^{3}}_{j}-{{r}^{3}}_{j-1}){{\rho }_{j}},$ |
Pi表示第i层中的静岩压力,ρi为第i层的密度,ri为第i层外表面的半径,Ai为第i层外表面处的压强.这里使用A34=0即月球表面的静岩压力为0作为边条件.
由此可以得到重力加速度和静岩压力随半径的变化如图 6所示.

|
Download:
|
| 图 6 重力加速度(a)和静岩压力(b)随半径的变化 Fig. 6 (a) Gravity vs. radius; (b) lithostatic pressure vs. radius | |
经计算得到在1000km深处岩体静压大约为3.9GPa,大体相当于地球岩石圈底部的围压.在这样的围压下,如果库伦-莫尔破裂准则τ=τ0+μ(σn-p)中的摩擦系数μ为0.6,则差应力需要达1GPa以上,远大于潮汐部分的差应力(1.8 × 105Pa).如此小的差应力很难成为主导月震发生的原因,但是我们又确实观察到破裂与潮汐有关.这一问题需要继续研究,我们估计有两种可能性,一是在月震多发区存在孔隙流体和高孔隙流体压力,使此区域需要的差应力大幅度减少;二是存在别的机制在这些区域产生足够大的差应力,潮汐作用在此巨大差应力的基础上触发月震.
另一方面,深源月震的体波震级多为1~2级,较大的也不过在3级左右,月震释放的能量最大约为106J[17-18],那么潮汐变形所积累的能量是否足以提供月震所需的能量呢?由于大的月震震矩大约为5 × 1013N·m[18],故其矩震级约为3级,利用地震震级与破裂面长度之间的经验关系:lg(RLD)=a+b×M,其中a=-2.44,b=0.59,RLD为破裂长度,M为矩震级[19],可以得出破裂长度约为0.214km,于是一个包含破裂面的立方体体积大约为107m3,根据我们计算的结果,潮汐变形积累的能量密度最大约为0.34J/m3,那么在这个包含破裂面的立方体中潮汐变形所积累的应变能大约为3.4 × 106J,与月震释放的能量相当.
通过以上2个模型的计算,可以看出当月球内部存在液态介质时,由于潮汐作用而引起的剪应力会在靠近液态介质的外侧集中,例如模型1的液核外侧、模型2的下月幔底部外侧,而根据目前所掌握的月震资料来看,700~1100km为月震的频发区,说明在此深度存在着剪应力的集中,而1100km深度以下没有检测到月震,说明此深度以下可能处于熔融或部分熔融的状态.这里有两种可能性.一种是液态月核半径的大小约为700多km.关于月核的大小目前没有确切的估计,柯宝贵[13]估计704~356km,如果月核半径为700多km,则1000km左右深度恰好为应力集中区.另外一种可能是月核半径小于700km,但月幔底部处于部分熔融状态,如同地球存在岩石圈和软流圈一样,可能月幔下部也存在软的圈层,其上界面大体位于1000km深度.由于月球热流测量数据十分有限,Apollos 15 和 17的钻孔测量结果分别为 21和 14 mW·m-2,因此对于月球深部介质的状态至今仍有争论,不同学者通过不同途径对月球所处的热状态进行计算[20-25],多数认为1000km深处的温度在1200℃左右,在此情况下不会存在熔融状态.不过也有不同的模型计算出的温度高于1200℃,并认为在950km深度月球介质处于部分熔融状态[22],与本文上述所作的假设相符合.
月球深震往往汇聚于一些特定区域成团组[6, 26-28],这与我们计算的剪应力区有象限性(例如图 5)也可能有关.将来如果对深震机制有更好的了解,有助于比较不同位置的震群与潮汐应力的力学联系.
1100km以下月震资料的缺乏,造成对此深度范围月球结构的了解困难,但月球深震的发生,包含了极其丰富的信息,而且我们仍然没能很好地了解.本文仅仅是一个初步探讨,但为月球深部结构的研究提出了另一条思路.
| [1] | Lognonné P, Mosser B. Planetary seismology[J]. Surveys in Geophysics , 1993, 14 (3) :239–302. DOI:10.1007/BF00690946 |
| [2] | Wieczorek M A, Jolliff B L, Khan A, et al. The Constitution and Structure of the Lunar Interior[J]. Reviews in Mineralogy and Geochemistry , 2006, 60 (1) :221–364. DOI:10.2138/rmg.2006.60.3 |
| [3] | Bulow R C, Johnson C L, Bills B G, et al. Temporal and spatial properties of some deep moonquake clusters[J]. Journal of Geophysical Research , 2007, 112 (E9) . |
| [4] | Koyama J. Chaotic occurrence of some deep moonquakes // 36th Annual Lunar and Planetary Science Conference, 2005,36: 1077. http://cn.bing.com/academic/profile?id=1679037592&encoded=0&v=paper_preview&mkt=zh-cn |
| [5] | Bills B G, Bulow R, Johnson C L. Influence of earth-moon orbit geometry on deep moonquake occurrence times[C]//Lunar and Planetary Institute Science Conference Abstracts. 2008: 1735. |
| [6] | Frohlich C, Nakamura Y. Geographic variations in the tidal control of deep moonquake nests and speculation about their mechanical origin[C]//Lunar and Planetary Institute Science Conference Abstracts. 2007, 38: 1749. |
| [7] | 丰海. 利用重力场和地形数据反演月壳厚度[J]. 大地测量与地球动力学 , 2009, 29 (3) :131–134. |
| [8] | 朱桂芝, 张怀, 石耀霖. 优化地球三维有限元计算网格的一种方法[J]. 中国科学院研究生院学报 , 2006, 23 (5) :676–680. |
| [9] | 陈绍林, 张怀, 朱桂芝, 等. 自转速率快速变化引起的全球位移场和应力场[J]. 地震 , 2008, 28 (4) :1–12. |
| [10] | Khan A. A new seismic velocity model for the moon from a Monte Carlo inversion of the Apollo lunar seismic data[J]. Geophysical Research Letters , 2000, 27 (11) :1591–1594. DOI:10.1029/1999GL008452 |
| [11] | Lognonn P, Gagnepain-Beyneix J, Chenet H. A new seismic model of the moon: implications for structure, thermal evolution and formation of the Moon[J]. Earth and Planetary Science letters. , 2003, 211 (1/2) :27–44. |
| [12] | Gagnepain-Beyneix J, Lognonn P, Chenet H, et al. A seismic model of the lunar mantle and constraints on temperature and mineralogy[J]. Physics of The Earth and Planetary Interiors , 2006, 159 (3/4) :140–166. |
| [13] | 柯宝贵. 应用Lane-Emden方程分析下月幔厚度与月核半径大小[J]. 地球物理学报 , 2009, 52 (5) :1208–1213. |
| [14] | 占伟, 李斐. 月球内部构造研究综述[J]. 地球物理学进展 , 2007, 22 (3) :737–742. |
| [15] | 张承志. 月球和火星内部结构模型的比较[J]. 南京大学学报:自然科学版 , 1990, 24 (4) :575–587. |
| [16] | 欧阳自远. 月球科学概论[M]. 北京: 中国宇航出版社, 2005 . |
| [17] | Latham G, Ewing M, Dorman J, et al. Moonquakes and lunar tectonism[J]. Earth, Moon, and Planets , 1972, 4 (3) :373–382. |
| [18] | Goins N R, Dainty A M, Toksoz M N. Seismic energy release of the moon[J]. Journal of Geophysical Research , 1981, 86 :378–388. DOI:10.1029/JB086iB01p00378 |
| [19] | Wells D L, Coppersmith K J. New empirical relationships among magnitude, rupture length, rupture width, rupture area, and surface displacement[J]. Bulletin of the Seismological Society of America , 1994, 84 (4) :974–1002. |
| [20] | Hanks T C, Anderson D L. Origin, evolution and present thermal state of the Moon[J]. Physics of The Earth and Planetary Interiors , 1972 (5) :409–425. |
| [21] | Tozer D C. The moon's thermal state and an interpretation of the lunar electrical conductivity distribution[J]. Earth, Moon, and Planets , 1972, 5 (1) :90–105. |
| [22] | Toksöz M N, Solomon S C. Thermal history and evolution of the Moon[J]. Earth, Moon, and Planets , 1973, 7 (3) :251–278. |
| [23] | Khan A. Constraining the composition and thermal state of the moon from an inversion of electromagnetic lunar day-side transfer functions[J]. Earth and Planetary Science Letters , 2006, 248 (3/4) :579–598. |
| [24] | Khan A, Maclennan J, Taylor S R, et al. Are the earth and the moon compositionally alike? Inferences on lunar composition and implications for lunar origin and evolution from geophysical modeling[J]. Journal of Geophysical Research , 2006, 111 (E05005) . DOI:10.1029/2005JE002608 |
| [25] | Khan A. Joint inversion of seismic and gravity data for lunar composition and thermal state[J]. Geophysical Journal International , 2007, 168 (10) :243–258. |
| [26] | Nakamura Y. A1 moonquakes:Source distribution and mechanism[C]//Lunar and Planetary Science Conference Proceedings.1978, 9: 3589-3607. |
| [27] | Nakamura Y. New identification of deep moonquakes in the Apollo lunar seismic data[J]. Physics of The Earth and Planetary Interiors , 2003, 139 :197–205. DOI:10.1016/j.pepi.2003.07.017 |
| [28] | Nakamura Y. Within-nest hypocenter distribution and waveform polarization of deep moonquakes and their possible implications [C]//Lunar and Planetary Institute Science Conference Abstracts. 2007,38:1160. |
 2016, Vol. 33
2016, Vol. 33 


