在磁约束热核聚变反应堆中,包层是能量转换的关键部件[1].金属流体在包层内的矩形通道中流动时,受外界强磁场影响产生独特的磁流体动力学(magnetohydrodynamics,MHD)速度分布和不稳定性,会强烈影响包层内流体的传热传质过程,从而影响包层乃至整个聚变装置的能量转换效率和安全性.因此,研究矩形截面通道中,金属流体在磁场作用下,流动的稳定性对聚变堆的设计及未来的安全运行都有重要的理论指导意义.
在垂向磁场影响下,液态金属在矩形截面管道中流动的速度分布受到管壁导电性质的影响很大.在矩形截面管道的4个壁面中,垂直于磁场的2壁面称为Hartmann壁,平行于磁场的壁面称为侧壁.Hartmann壁和侧壁处的边界层分别为Hartmann层和侧层.当两Hartmann壁导电,侧壁绝缘时,流动称为Hunt’s 流[2];若4个壁面均为绝缘壁,则流动称为Shercliff 流[3].以上2种流动已得到相应的解析解.2014年,陶震等[4]得到了方管中相对的2壁面导电性质不对称的MHD流动的解析解.他们发现,当管道的Hartmann壁理想导电,而2侧壁导电性质不对称时,流动只会在绝缘的侧壁附近出现射流,其速度和电流分布均会出现不对称的性质,这与前面提到的几种流动有较大区别.
近年来,国内外学者对Hunt’s流、Shercliff流及理想导电方管中流动的稳定性问题做了较多研究.Priede等对Hunt’s流[5]及理想导电方管中的MHD流动[6]分别做了线性稳定性分析,得到4种最不稳定模态的临界雷诺数Rec与Hartmann数间的渐进关系式.Smolentsev 等 [7]对有近壁射流和速度拐点的方管流动进行了稳定性研究,将M型速度分布简化为准二维流动来处理,发现拐点不稳定和高雷诺数时由Tollmien-Schlichting波引起的侧层不稳定是流动最主要的2种不稳定机制.Pothérat[8]、Victor等[9]及Krasnov [10]分别对Shercliff流的稳定性进行了研究,发现此次流动中最不稳定的线性模态(Tollmien-Schlichting波)及Hartmann层与侧层对扰动瞬态增长的不同影响.
以上研究均是针对对称的MHD方管流动进行的,而对于陶震得出的不对称流动的稳定性问题,至今还没有人做过分析.对侧壁导电性质不对称的方管MHD流动,其速度分布中存在一个射流,研究此流动的线性稳定性对进一步探究射流发生不稳定的物理机理有重要意义.因此,本文分析了Hartmann壁理想导电、2侧壁导电性质不对称的MHD方管流动的线性稳定性问题.应用线性稳定性理论得到特征值问题,采用Chebyshev配置法进行求解,详细分析了不同强度的磁场影响下,流动发生不稳定的物理机制.
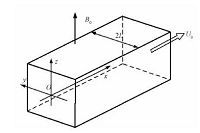
1 理论模型及求解方法本文研究的是外加均匀磁场作用下,压差驱动的液态金属在方截面通道中的充分发展层流.如图 1所示,流动沿x方向,外加磁场B=B0eB沿z方向,通道截面边长为2L.垂直于磁场的两壁面为理想导电,平行于磁场的两壁面中,左壁面理想导电,右壁面绝缘.为简单起见,我们把所研究的这种MHD流动称为Hunt-I流.
|
Download:
|
| 图 1 流动示意图 Fig. 1 Geometry and coordinates | |
该流动的无量纲控制方程为
| $\Delta \cdot v=0$ | (1) |
| $\frac{\partial v}{\partial t}+\left( v\cdot \Delta \right)v=-\Delta p+\frac{1}{Re}{{\Delta }^{2}}v+\frac{H{{a}^{2}}}{Re}(J\times {{e}_{B}}),$ | (2) |
| $\Delta \cdot J=0,$ | (3) |
| $J=-\Delta \varphi +v\times {{e}_{B}},$ | (4) |
其中,v=(u,v,w),J=(Jx,Jy,Jz),p,φ分别为流动的速度矢量、电流密度矢量、压力和电势.本文取特征长度为L,特征速度为流动的最大速度U0,压强、电流密度及电势的特征尺度分别为ρU02,σU0B0和U0LB0.磁感应强度的特征尺度为外加磁感应强度B0.此问题涉及的无量纲参数有:雷诺数Re=ρU0L/μ,表征惯性力与黏性力之比;Hartmann数
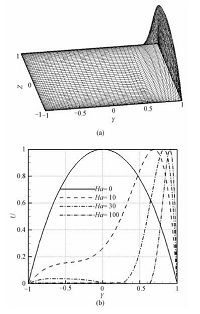
该流动中,速度在壁面边界处满足无滑移边界条件v|s=0,电势边界条件为绝缘壁面处,∂nφ|s=0,理想导电壁面处,φ|s=0.该流动的速度场已由陶震等的解析解给出,其速度分布如图 2所示,随磁场增强,在绝缘侧壁附近会出现一股射流,且该射流在流动展向上的厚度逐渐减小.
|
Download:
|
| 图 2 (a) Ha=100时Hunt-I流的三维速度分布图; Fig. 2 (a) 3D velocity profile of Hunt-I flow for Ha=100; | |
当流动受到轻微扰动时,各物理量可表示为
| $\left( v,p,\varphi \right)=({{V}_{0}},{{P}_{0}},{{\Phi }_{0}})+v\prime ,p\prime ,\varphi \prime $ | (5) |
其中,v′,p′,φ′分别为速度、压力及电势的扰动量.将(5)式代入方程(1)—(4)中,根据线性稳定性理论,略去高阶小量,得以下小扰动线化方程:
| $\frac{\partial u\prime }{\partial x}+\frac{\partial v\prime }{\partial y}+\frac{\partial w\prime }{\partial z}=0,$ | (6) |
| $\begin{align} & \frac{\partial u\prime }{\partial t}+{{U}_{0}}\frac{\partial u\prime }{\partial x}+v\prime \frac{\partial {{U}_{0}}}{\partial y}+w\prime \frac{\partial {{U}_{0}}}{\partial z}=-\frac{\partial p\prime }{\partial x}+ \\ & \frac{1}{Re}{{\Delta }^{2}}u\prime +\frac{H{{a}^{2}}}{Re}\left( -\frac{\partial \varphi \prime }{\partial y}-u\prime \right), \\ \end{align}$ | (7) |
| $\frac{\partial v\prime }{\partial t}+{{U}_{0}}\frac{\partial v\prime }{\partial x}=-\frac{\partial p\prime }{\partial y}+\frac{1}{Re}{{\nabla }^{2}}v\prime +\frac{H{{a}^{2}}}{Re}\left( \frac{\partial \varphi \prime }{\partial x}-v\prime \right),$ | (8) |
| $\frac{\partial w\prime }{\partial t}+{{U}_{0}}\frac{\partial w\prime }{\partial x}=-\frac{\partial p\prime }{\partial z}+\frac{1}{Re}{{\nabla }^{2}}w\prime ,$ | (9) |
| ${{\nabla }^{2}}\varphi \prime =\frac{\partial v\prime }{\partial x}-\frac{\partial u\prime }{\partial y}.$ | (10) |
其边界条件为
| $u\prime =v\prime =w\prime =0,\varphi \prime =0,z=\pm 1;$ | (11a) |
| $u\prime =v\prime =w\prime =0,\varphi \prime y=0,y=+1;$ | (11b) |
| $u\prime =v\prime =w\prime =0,\varphi \prime =0,y=-1.$ | (11c) |
本文考虑时间模式,则扰动量可展开为正则模形式:
| $\left[ u\prime ,v\prime ,w\prime ,p\prime ,\varphi \prime \right]=\left[ \hat{u},\hat{v},\hat{w},\hat{p},\hat{\varphi } \right]\left( y,z \right)\centerdot {{e}^{i\left( ax-wt \right)}}$ | (12) |
其中,
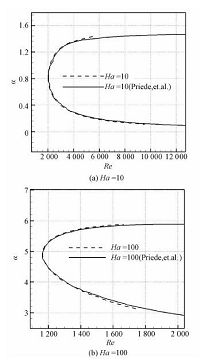
本文计算了Ha=10和Ha=100时Hunt’s流的中性曲线,并与Priede等数值计算的结果进行对比.如图 3所示,本文的计算结果与Priede等的结果符合较好,证明了本文所用程序的正确性.此外,通过在不同配置点数下计算所得的特征值进行对比发现,当配置点选为50×50时,所得特征值已精确到小数点后第5位,满足计算所需精度.因此本文计算选用配置点数为50×50.
|
Download:
|
| 图 3 本文计算所得Hunt’s流中性曲线(虚线)与Priede等的曲线(实线)对比 Fig. 3 Neutral stability curves of Hunt’s flow obtained based on our calculations (dashed lines) ,compared to the curves (solid lines) of Priede et al.[5] | |
通过求解第一章所构造的特征值问题,可求得一定参数条件下的特征值ω和特征函数.特征值的虚部ωi表示扰动随时间的增长率.若该增长率大于零,则扰动会随时间持续增长,使流动发生不稳定;若增长率小于零,则该扰动会随时间逐渐衰减,流动是稳定的;当增长率等于零时,流动将处于中性稳定状态.
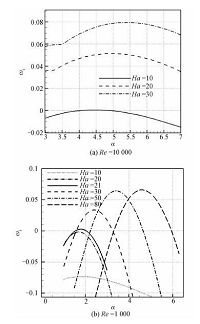
本文首先计算了Re=10000时,Ha=10,20,30时不同波数α对应的最不稳定扰动的增长率曲线,如图 4(a)所示.由图 4(a)可知,当Ha=10,α≈4.6时,扰动增长率略大于零,表明在此参数条件下,流动将发生线性不稳定.而随Ha由10增至30,扰动的增长率曲线整体上移,增长率随Ha数的增大而显著增大,这表明磁场增强时,此类扰动也会随之增强.但随Ha数增大,发现还存在另一种模态的扰动,使流动在较低Re数(Re≈1000)时就会发生线性不稳定性.
|
Download:
|
| 图 4 扰动增长率曲线 (ωi vs. α) Fig. 4 Growth rate curves (ωi vs. α) for Re=10000(a) and Re=1000(b) | |
我们绘出Re=1000时,Ha=10,20,21,30,50,80时,最不稳定扰动的增长率ωi随波数变化的曲线,如图 4(b)所示.由图 4(b)可知,当Ha=10和20时,增长率恒小于零,表明此时该模态的扰动是线性稳定的.而当Ha增大到21以上时,扰动增长率峰值大于零.综合图 4(a)、图 4(b)可知,当Ha≤20时,流动的线性不稳定性在较高Re数(Re≈10000)时才会发生,而当Ha≥21时,流动不稳定性在较低Re数(Re≈1000)下就会出现.由此可推测在这2种Ha数范围内发生的不稳定性是由不同模态的扰动引起的.在Ha≥21条件下起主导作用的扰动会随Ha数的减小逐渐衰减,而另一种在高Re数时起作用的扰动,会成为导致Ha≤20时流动失稳的主导模态.当Ha数取20至21之间某值时,流动中的最不稳定模态将在这2种模态间发生交替.为证实这一推测并进一步分析不稳定机理,我们画出了不同Ha数下扰动在管道截面上的空间分布图.
2.3 扰动空间分布随Ha数的变化
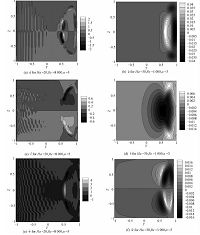
图 5所示为Ha=20和30时,速度扰动量在通道截面上的空间分布图.其他参数设为Re=1000,α=3.由图 5(a)、(c)、(e)可知,当Ha=20时,速度的扰动量
|
Download:
|
|
图 5 Ha=20和30时,速度扰动量在管道截面上的分布图
Fig. 5 Distributions of perturbed velocity |
|
当Ha=20时,扰动集中在射流速度出现拐点的区域,此时扰动是由拐点附近强烈的速度剪切引起的,为拐点不稳定性[7].当Ha=30时,拐点不稳定性依然存在并起较重要作用.但同时,随磁场增强,射流在y方向上的厚度减小,侧层内的速度梯度增加,黏性效应显著.因而侧层内会出现由Tollmien-Schlichting波引发的不稳定性.同时,射流在靠近Hartmann壁处,沿z方向也存在较大的速度梯度,也会在一定条件下产生Tollmien-Schlichting波,并由此引发流动不稳定.因而图 5(b)、图 5(d)中在射流两端处也会出现扰动速度的极值.此外,由于基本流中射流沿z方向速度的非均匀性(中部速度远大于两端速度),速度拐点处及速度梯度较大处产生的扰动会受到这种速度分布的拉伸,从而使扰动得到增强.
因此,当Ha=20时,拐点不稳定性是流动中起主导作用的线性不稳定机制.而当Ha=30时,流动的线性不稳定性是由以下3种效应共同作用产生的:1)射流靠近核心区处的速度拐点会产生不稳定波;2)侧层内及射流靠近Hartmann壁处存在的速度剪切诱导产生Tollmien-Schlichting波;3)射流沿z方向速度分布的非均匀性会增强前两种效应产生的扰动,促进流动发生不稳定.
2.4 Hunt’s流与Hunt-I流的对比我们计算了Ha=10,Re=11000,α=5和Ha=70,Re=2000,α=5时,Hunt’s流与Hunt-I流的速度扰动量在通道横截面上的分布,如图 6所示.由图 6可知,当Ha=10时,Hunt-I流的扰动分布在射流靠近核心区一侧的拐点处;Hunt’s流扰动也集中在拐点附近,但因Ha数较小,流动中2射流的速度拐点距离较近,它们周围的扰动会相互影响,并产生合并,形成中心处的一列扰动,如图 6(b)所示.而当Ha增大时,Hunt’s流中的射流会沿展向变薄,2速度拐点处的扰动不再有相互作用.当Ha=70时,如图 6(e)—图 6(h),Hunt’s流与Hunt-I流内扰动的分布规律相同,即除了在拐点附近外,扰动还贯穿整个侧层,并且在侧层靠近Hartmann壁的两端处出现2个极大值点.这表明,在较高Ha数(Ha=70)下,2种流动的不稳定都是由2.3节所分析的综合模态引起的.而当Ha较低时(Ha=10),Hunt’s流内的扰动会因相互作用而融合成为沿z方向的一列涡;而Hunt-I流的扰动集中在射流的速度拐点处,与Hunt’s流扰动分布有明显区别.

|
Download:
|
|
图 6 Ha=10,Re=11000,α=5和Ha=70,Re=2000,α=5时,Hun't′s流与Hunt-I流的速度扰动量在通道截面上的分布图
Fig. 6 Distributions of perturbed velocity of Hunt’s flow (a)û and (b) |
|
本文研究垂向磁场影响下,液态金属在方截面通道中受压差驱动充分发展流动的线性稳定性问题.通道的两Hartmann壁为理想导电体,左侧壁理想导电,右侧壁绝缘.该流动的解析解已由陶震等给出.本文依据线性稳定性理论,导出小扰动线化方程,得到广义特征值问题.采用2D-Chebyshev配置法求解此特征值问题,绘出了扰动增长率曲线及速度扰动量的空间分布图.由计算结果总结出以下结论:
1) 流动中存在2种主要不稳定模态.当Ha数增大到20至21之间某值时,起主导作用的模态发生交替.
2) Ha≤20时,流动中拐点不稳定性起主导作用;Ha≥21时,不稳定性由一种综合模态引起.其中,速度拐点及侧层内的强速度剪切会诱导产生不稳定波,而射流沿z方向速度的不均匀性使扰动波受到拉伸和增强,从而引起流动的不稳定性.
3) 低Ha数(Ha≈10)下,Hunt’s流内2射流拐点引发的扰动会相互作用并融合;而当Ha较高时,Hunt’s流与Hunt-I流的不稳定系由上述综合模态引起.
| [1] | Smolentsev S, Moreau R, Abdou M. Characterization of key magnetohydrodynamic phenomena in PbLi flows for the US DCLL blanket[J]. Fusion Engeering and Design , 2008, 83 (5) :771–783. |
| [2] | Hunt J C R. Magnetohydrodynamic flow in rectangular ducts[J]. Journal of Fluid Mechanics , 1965, 21 (4) :577–590. DOI:10.1017/S0022112065000344 |
| [3] | Shercliff J A. Steady motion of conducting fluids in pipes under transverse magnetic fields[J]. Mathematical Proceedings of the Cambridge Philosophical Society , 1953 (1) :136–144. |
| [4] | Tao Z, Ni M J. Analytical solutions for MHD flow at a rectangular duct with unsymmetrical walls of arbitrary conductivity[J]. Science China Physics, Mechanics Astronomy , 2015, 58 (2) :024701. |
| [5] | Priede J, Aleksandrova S, Molokov S. Linear stability of Hunt's flow[J]. Journal of Fluid Mechanics , 2010, 649 :115. DOI:10.1017/S0022112009993259 |
| [6] | Priede J, Aleksandrova S, Molokov S. Linear stability of magnetohydrodynamic flow in a perfectly conducting rectangular duct[J]. Journal of Fluid Mechanics , 2012, 708 :111–127. DOI:10.1017/jfm.2012.276 |
| [7] | Smolentsev S, Vetcha N, Moreau R. Study of instabilities and transitions for a family of quasi-two-dimensional magnetohy-drodynamic flows based on a parametrical model[J]. Physics of Fluids , 2012, 24 (2) :024101. DOI:10.1063/1.3680864 |
| [8] | Pothérat A. Quasi-two-dimensional perturbations in duct flows under transverse magnetic field[J]. Physics of Fluids , 2007, 19 (7) :319–345. |
| [9] | Shatrov V, Gerbeth G. Marginal turbulent magnetohyd-rodynamic flow in a square duct[J]. Physics of Fluids , 2010, 22 (8) :585–591. |
| [10] | Krasnov D, Zikanov O, Rossi M, et al. Optimal linear growth in magnetohydrodynamic duct flow[J]. Journal of Fluid Mechanics , 2010, 653 (6) :273–299. |
| [11] | Jun H, Henry D, Yin X Y, et al. Linear biglobal analysis of Rayleigh-Bénard instabilities in binary fluids with and without throughflow[J]. Journal of Fluid Mechanics , 2012, 713 (6) :216–242. |
 2016, Vol. 33
2016, Vol. 33 


