自本世纪起,作为对VaR的改进,Rockafellar和Uryasev[1]提出CVaR (conditional value-at-risk)概念,并以此作为风险度量来建立投资组合的优化模型.在此基础上,许多学者[2-5]作出了一系列工作,使得这方面的研究内容越来越丰富.本文把广义熵作为一个约束条件,并采用K-means聚类方法来生成投资组合中各个资产的未来收益率情景和概率,以此构建基于CVaR风险度量的投资组合模型,使之达到更好的效果.
1 模型的建立 1.1 基于广义熵约束的CVaR投资组合优化模型我们知道,Tsallis 广义熵的形式如下
| $Hp=\frac{1}{\alpha -1}1-\sum\limits_{i=1}^{n}{{{p}^{\alpha }}_{i},\alpha \ne 1,{{p}_{i}}\ge 0,i=1,2,\ldots ,n,}\sum\limits_{i=1}^{n}{{{p}_{i}}=1},$ | (1) |
其中,α是广义熵模型中的参数,取值在0~1之间,1-α表示投资者的风险厌恶程度.
假设投资组合P包含n个风险资产,其中,w=(w1,w2,…,wn)T表示投资权重向量.Rockafellar和 Uryasev[6]通过构造一个如(2)式所示的、满足凸性的函数,这样就能把以CVaR作为目标函数的问题转化为以该凸性函数为目标函数的问题
| ${{G}_{\alpha }}w,\zeta =\zeta +1-{{\alpha }^{-1}}\int Lw,X-{{\zeta }^{+}}pXdX.$ | (2) |
这里ζ表示一定置信水平下,投资组合所允许的最大损失,即VaR,X∈Rn是投资组合P的收益率向量,Lw,X是组合P的损失函数[6],通常表示为
| $Lw,X=-{{w}^{T}}X.$ | (3) |
而Lw,X-ζ+=max {Lw,X-ζ,0}.p(X)是X的密度函数,α是置信水平(比如可取值0.95、0.99等),从下面的实证可以看出,它与广义熵中的α意义相同,即1-α表示投资者的风险厌恶程度.由于Gαw,ζ关于w,ζ是凸的[6],所以(2)式也避免了多重极值的问题.
现在我们根据Krokhmal等[7]的转化方法.设随机向量X的J个收益率情景是:X1,X2,…,XJ.则Gαw,ζ经过离散化处理可近似为
| ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G}}_{\alpha }}w,\zeta =\zeta +1-{{\alpha }^{-1}}\sum\limits_{j=1}^{J}{{{p}_{j}}{{[-{{w}^{T}}{{X}_{j}}-\zeta ]}^{+}},}$ | (4) |
其中,pj表示情景Xj发生的概率.若用函数
| $\begin{align} & mi{{n}_{(w,\zeta )}}\zeta +{{\left( 1-\alpha \right)}^{-1}}\sum\limits_{j=1}^{J}{{{p}_{j}}{{z}_{j}},s.t.~w\in W,} \\ & \sum\limits_{j=1}^{J}{{{p}_{j}}{{w}^{T}}{{X}_{j}}\ge {{r}_{p}},{{z}_{j}}\ge 0,j=1,2,\ldots ,J,{{z}_{j}}\ge -{{w}^{T}}{{X}_{j}}-\zeta ,j=1,2,\ldots ,J,} \\ \end{align}$ | (5) |
其中,rp表示投资组合的最低收益率.在现实的股票交易中,通常还需要考虑佣金、印花税之类的交易费用.现假设风险资产的费用率为k,并假设初始投资权重为零向量,则组合P的交易费用为
| $c=k\sum\limits_{i=1}^{n}{\left| {{w}_{i}}-{{w}^{0}}_{i} \right|}=k\sum\limits_{i=1}^{n}{\left| {{w}_{i}} \right|=k}.$ | (6) |
另外,中国投资市场还没有广泛推行卖空机制,所以本文模型中添加了卖空的限制.于是在考虑卖空限制、交易成本、投资者的风险厌恶程度和广义熵约束后,得到最终的CVaR的投资组合优化模型
| $\begin{align} & mi{{n}_{(w,\zeta )}}\zeta +{{\left( 1-\alpha \right)}^{-1}}\sum\limits_{j=1}^{J}{{{p}_{j}}{{z}_{j}},s.t.~{{w}_{i}}\ge 0,i=1,2,\ldots ,n,}\sum\limits_{i=1}^{n}{{{w}_{i}}=1,} \\ & \frac{1}{\alpha -1}\left( 1-\sum\limits_{i=1}^{n}{{{w}^{\alpha }}_{i}} \right)\ge \beta ,\sum\limits_{j=1}^{J}{{{p}_{j}}{{w}^{T}}{{X}_{j}}-k\ge {{r}_{p}}},{{z}_{j}}\ge 0,j=1,2,\ldots ,J,{{z}_{j}} \\ & \ge -{{w}^{T}}{{X}_{j}}-\zeta ,j=1,2,\ldots ,J, \\ \end{align}$ | (7) |
其中,β表示投资组合广义熵的最小值.这是一个容易求解的带有非线性约束的线性规划问题,可以通过MATLAB中的fmincon函数进行求解.细心的读者可能发现本文构建的模型需要投资组合中各个资产的未来收益率的情景和相应的每个情景发生的概率作为模型输入,但传统的模拟方法是将每个收益率情景发生的概率当作是均等的,这显然不符合现实情况.于是本文考虑以各个资产的收益率的历史数据运用K-means 聚类算法来模拟它们的未来收益率的情景,并获得相应情景发生的概率.
需要指出的是,由于影响证券收益率水平的因素很多,如银行基础利率、证券市场上货币供求关系、市场牛熊阶段和上市公司自身经营状况等,而且这些因素均是时变的,所以,来源于历史数据未来收益率的情景描述是一个考虑了这些因素的平均结果.当然分别考虑各时段单个因素的影响,将会使得模型运算更加准确,也更加有效,但其复杂性亦会更大.所以我们将把这作为以后研究的方向,这里先不讨论.
1.2 K-means聚类算法现在我们用K-means聚类算法生成随机向量X的J个收益率情景X1,X2,…,XJ.首先收集投资组合中各个资产的历史收益率数据,然后设定聚类的个数和允许的误差范围,其中聚类个数即是所需要的情景个数.通过SPSS统计软件中K-means聚类功能可以得到聚类的结果和每个类中的历史收益率的个数.把各个类的中心作为未来收益率的情景,通过每个类中的收益率个数可以得出每个场景发生的概率,以此作为本文模型的输入.可以证明,在欧式距离下,K-means算法所得到的分类结果满足每个类都是凸的,这样保证了用这个方法分解所得到的同一类内事物之间比较接近[9].
2 实证分析 2.1 数据处理和运行本文选取在深市挂牌交易年份比较早的8只股票(取自国泰安数据库):平安银行(000001)、西安民生(000564)、万科(000002)、云南白药(000538)、合肥美菱(000521)、泸州老窖(000568)、国元证券(000728)和中国长城计算机(000066),它们来自不同行业,满足投资者分散化投资的要求.选取每只股票1998年1月1日至2013年12月31日的日收盘价数据,则每只股票有3577个数据,相应地计算出每只股票的日对数收益率 3576个数据.根据这些数据,我们应用SPSS软件依据K-means聚类的思想生成各只股票的收益率250个情景,相应得到收益率矩阵X=xij250×8和对应的概率矩阵P=(pij)1×250.表 1给出这个聚类结果的一部分.最后利用MATLAB数学软件将模型(7)编写成fmincon函数,以其求出最优权数w和CVaR.
|
|
表 1 J=250时情景数值表中前18个情景及概率 Table 1 The former 18 scenarios and probabilities in the scenario value table when J=250 |
将不同置信水平CVaR随收益率水平变化而变化的情况在同一张图中展示出来,如图 1所示.可以看出,随最低目标收益率水平的不断增加,CVaR也呈现出不断增加的趋势,符合高收益、高风险的投资原理.并且在同一目标收益率水平下,随置信水平的不断增加,CVaR也不断增加.反映出投资者的风险厌恶程度越低,所能承担的风险越大,即1-α越小,CVaR越大,符合投资者投资的现实情况.

|
Download:
|
| 图 1 不同置信水平下的最低目标收益率与CVaR Fig. 1 The minimum target return rate and CVaR at different confidence levels | |
置信水平α=0.95时,最低目标收益率rp变动时的VaR、CVaR、最优投资权重,如表 2所示.w1,w2,w3,w4,w5,w6,w7,w8分别表示平安银行、西安民生、万科、云南白药、合肥美菱、泸州老窖、国元证券和中国长城计算机的投资权重.
|
|
表 2 不同收益率水平下投资组合的最优投资权重和CVaR值 Table 2 The optimal investment weight and CVaR value at different yield levels |
投资组合中每只股票都有相应的权重,如在最低预期收益率水平较低为0.028%时,对平安银行、西安民生、云南白药、泸州老窖、国元证券5只股票的投资权重相对较高,但是对其中每一只股票的投资都在12%~ 17%,对其他3只股票的投资比例相对较少,分别是6.428%、10.235%和9.521%,体现了分散化投资的原则.但是随着最低目标收益率水平的增加,投资组合中的各只股票的投资权重也相应发生变化.
与MV模型得到的结果进行比较如表 3所示.
|
|
表 3 MV模型与本文模型投资组合的最优投资权重比较 Table 3 Comparison of optimal investment weight between MV model and the present model |
可以看出在某一目标收益率水平约束下,由MV方法得出的投资组合中各只股票的投资比重相差很大,无论收益率如何,投资组合都没有对平安银行、中国长城计算机2只股票的投资.随着最低目标收益率水平的增加,MV模型对云南白药的投资比例变得非常大,而对其他5只股票的投资比例急剧减少,这使得由MV模型得到投资组合的风险非常大.而用本文中基于广义熵约束的CVaR风险度量模型得到的投资组合的最优投资权重较为分散.所以相比较而言,本文基于广义熵约束的CVaR风险度量的投资组合优化模型显现出了分散化投资的原则,即在满足了投资者的最低目标收益率水平下,对应的投资风险最小.
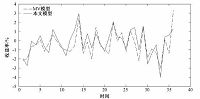
最后,本文运用2014年1月1日至2014年2月28日的8只股票36个日对数收益率,比较MV模型和本文模型得到的最优投资组合在未来收益的表现情况,由图 2和图 3可以看出,由本文模型得到的最优投资组合收益情况表现比MV模型更好,这体现了基于广义熵约束的CVaR投资组合模型的较强实用性.
|
Download:
|
| 图 2 rp=0.00028时MV模型与本文模型未来收益率对比 Fig. 2 Comparison of future return rate between MV model and the present model when rp=0.00028 | |

|
Download:
|
| 图 3 rp=0.00028时MV模型与本文模型未来累积收益率对比 Fig. 3 Comparison of future cumulative return rate between MV model and the present model when rp=0.00028 | |
本文综合考虑投资者的风险厌恶程度、交易费用、卖空限制等现实投资情况,通过线性化、离散化操作,把基于广义熵约束的CVaR投资组合模型转化成一个易于求解的线性规划模型,应用SPSS软件产生基于K-means聚类法的单阶段投资组合中各只股票收益率作为模型输入,运用MATLAB软件编程得到投资组合的最优权数和CVaR.通过与MV模型结果的比较发现,本文模型得到的投资组合中各只股票的投资比例更加分散,这极大地降低了投资组合的风险.比较MV模型和本文模型得到的最优投资组合在未来收益的表现情况可以发现,由本文模型得到的最优投资组合在未来收益表现情况更好,体现了基于广义熵约束的CVaR投资组合模型的较强实用性.
本文在收益率的情景聚类中存在不足之处,还需要进一步的完善,例如可以考虑用K-means聚类法生成投资组合中各个资产的多阶段收益率的情景,以使投资权重可以实现动态化,我们以后会进一步完善模型,使模型更具实用性.
| [1] | Rockafellar R T, Uryasev S. Optimization of conditional value-at-risk[J]. Journal of Risk , 2000, 2 (3) :21–41. DOI:10.21314/JOR.2000.038 |
| [2] | Elahi Y, Abd Aziz M l. Mean-variance-CVaR model of multiportfolio optimization via linear weighted sum method[J]. Mathematical Problem in Engineering , 2014 :1–7. |
| [3] | Meng Z Q, Jiang M, Hu Q Y. Dynamic CVaR with multi-period risk problems[J]. Journal of System & Complexity , 2011, 24 (5) :907–918. |
| [4] | 周世昊, 倪衍森. 求解CVaR投资组合优化问题之改进PSO算法[J]. 武汉理工大学学报 , 2010, 32 (1) :180–182. |
| [5] | 张茂军, 南江霞, 高爱华. 求解带有交易费用的CVaR投资组合模型的L-S算法[J]. 经济数学 , 2012, 29 (2) :74–78. |
| [6] | Rockafellar R T, Uryasev S. Conditional value-at-risk for general loss distributions[J]. Journal of Banking and Finance , 2002, 26 (7) :1443–1471. DOI:10.1016/S0378-4266(02)00271-6 |
| [7] | Krokhmal P, Palmquist J, Uryasev S. Portfolio optimization with condional value-at-risk objective and constraints[J]. The Journal of Risk , 2002, 4 (2) :124–129. |
| [8] | 刘俊山.基于风险测度理论的证券投资组合优化研究 [D].上海:复旦大学,2007. http://cdmd.cnki.com.cn/article/cdmd-10246-2007168760.htm |
| [9] | 魏法明.基于随机规划动态投资组合中的情景元素生成研究 [D]. 上海:同济大学,2008. |
 2016, Vol. 33
2016, Vol. 33