本文主要研究紧黎曼面上的HCMU度量问题.
1 背景和主要定理一般意义上的extremal Kähler度量最早由Calabi在文献[1]中提出,目的是在一个紧Kähler流形的固定Kähler类 中找到最好的度量.具体地,设M为一个紧Kähler流形,在一个固定的Kähler类中,extremal Kähler度量 是下述Calabi能量的临界点
| $C\left( g \right)={{\int }_{M}}{{R}^{2}}dg,$ |
这里R是Kähler类中度量g
| ${{R}_{,\alpha \beta }}=0,1\le \alpha ,\beta \le di{{m}_{c}}M,$ | (1) |
这里R,αβ是R的2阶(0,2)型协变导数.因此我们称在一个紧Kähler流形M上满足(1) 的度量为extremal Kähler度量.
当M是紧黎曼面时,Calabi在文献[1]中证明extremal Kähler度量就是常曲率(CSC)度量.自然地问题是如果在 紧黎曼面上extremal Kähler度量有奇点,是不是仍是常曲率度量.答案是否定的.在紧黎曼面上带奇点的extremal Kähler 度量 通常被称为HCMU(the Hessian of the curvature of the metric is umbilical)度量.文献[2]给出了只带cusp奇点的HCMU度量的 分类,其中在球面上确实存在非常曲率的HCMU度量.下文中我们简称非常曲率的HCMU度量为non-CSC HCMU度量.之后,文献[3]研究带锥奇点的non-CSC HCMU度量,研究了它的构造,并给出了一个这种HCMU度量存在的障碍性定理. 文献[4]给出带锥奇点的non-CSC HCMU度量的局部结构,证明了任何一个带锥奇点的non-CSC HCMU度量都是由一些 结构最简单的带锥奇点的non-CSC HCMU度量粘起来的,这种结构最简单的带锥奇点的non-CSC HCMU度量称为football.文献[4]还给出了任意两个 football能粘在一起的充要条件.接下来,文献[5]用复分析的方法给出了带锥奇点的non-CSC HCMU度量,得到了 任何一个带锥奇点的non-CSC HCMU度量都与一个底流形上特殊的亚纯1-形式有关,这种亚纯1-形式被称为该HCMU度量的 特征1-形式.文献[6]将文献[5]中的结果推广到了既带锥奇点又带cusp奇点的non-CSC HCMU度量上.
本文将利用上述结果研究两方面问题.第一是带锥奇点的non-CSC HCMU度量的存在性问题,第二是关于non-CSC HCMU度量 的能量积分问题.
第一个问题的结果如下:
定理1.1 令p1,p2,p3为S2上任意3个点,α1,α2,α3为正实数且都不为1.则在S2上存在以p1,p2,p3为 锥奇点并且锥角度分别为2πα1,2πα2,2πα3的non-CSC HCMU度量的充要条件为α1,α2,α3 中至少有一个整数.
第二个问题的结果如下:
定理1.2 设M为紧黎曼面,p1,p2,…,pN为M上N个点,g为M上non-CSC HCMU度量,并且以p1,p2,…,pN 为奇点. 又设K为g 的高斯曲率,{q1,q2,…,qS}⊂M\{p1,p2,…,pN}为K的光滑极值点集,ω为g的特征1-形式. 记M′=M\{p1,p2,…,pN,q1,q2,…,qS},令
| ${{C}_{n}}\left( g \right)={{\int }_{M}}_{\prime }{{K}^{n}}dg,n=0,1,2,\ldots ,$ |
称为g的第n个能量积分.则
| ${{C}_{n}}\left( g \right)=\frac{6{{\alpha }_{max~}}({{K}^{n+1}}_{1}-{{K}^{n+1}}_{2})}{\left( n+1 \right)({{K}_{1}}-{{K}_{2}})({{K}_{2}}+2{{K}_{1}})},$ |
这里αmax表示K的最大值点处的锥角度之和,K1和K2分别表示K的最大和最小值.
注:在定理1.2中,g可以是只带锥奇点的non-CSC HCMU度量,也可以是既带锥奇点又带cusp奇点的non-CSC HCMU度量. 事实上,文献[4]已经计算出了一个football的面积,再利用文献[4]中得到的任意 两个football能粘在一起的充要条件(见下文定理2.3),可以得到任何一个带锥奇点的non-CSC HCMU度量的面积.文献[5]定义了带锥奇点的non-CSC HCMU 度量的特征1-形式,并且说明利用特征1-形式也能计算出带锥奇点的non-CSC HCMU度量的面积和Calabi能 量,但是没有给出具体的公式.文献[6]将文献[5]的结果推广到了带锥奇点和cusp奇点的non-CSC HCMU度量上,也定义了相应的特征1-形式.定理1.2利用non-CSC HCMU度量的特征1-形式给出了只带锥奇点以及既带锥奇点又带cusp奇点的non-CSC HCMU 度量的第n个能量积分公式,自然也包括了面积和Calabi能量的表达式.
2 预备知识 2.1 HCMU度量,锥奇点和cusp奇点设M为紧黎曼面,p1,p2,…,pN为M上N个点.又设g是 M\{p1,p2,…,pN}上的光滑保角度量,如果g满足
| ${{\Delta }_{g}}K+{{K}^{2}}=C,$ | (2) |
这里K为g的高斯曲率,C为实常数,称g为M上extremal Hermitian度量.(2)等价于在局部复坐标系下有
| $\frac{\partial {{K}_{,zz}}}{\partial \bar{z}}=0,$ | (3) |
见文献[3].如果g满足在局部复坐标系下
| ${{K}_{,zz}}=0,$ | (4) |
称g为HCMU度量.明显HCMU度量一定是extremal Hermitian度量,并且HCMU度量就是extremal Kähler度量在M\{p1,p2,…,pN}上的直接推广.在下文中,我们一直假设extremal Hermitian度量和HCMU度量有有限的 面积和有限的Calabi能量,即
| ${{\int }_{M\backslash \{p}}_{1}{{,}_{{{p}_{2}},\ldots ,{{p}_{N}}\}}}dg<+\infty ,{{\int }_{M\backslash \{p}}_{1}{{,}_{{{p}_{2}},\ldots ,{{p}_{N}}\}}}{{K}^{2}}dg<+\infty .$ | (5) |
下面介绍锥奇点和cusp奇点:
定义2.1 设X为黎曼面,p∈X.又设(U,z)为p附近的局部复坐标系且z(p)=0,g为U\{p}上光滑度量.如果g=e2φ|dz|2,并且φ-(α-1)ln|z|(α >0)在p处连续,称p为g的锥奇点并且g在p处有锥角度2πα.
定义2.2 设X为黎曼面,p∈X.又设(U,z)为p附近的局部复坐标系且z(p)=0,g为U\{p}上的光滑度量.如果g=e2φ|dz|2,并且
事实上,如果HCMU度量满足(5),则它的奇点或者是锥奇点或者是cusp奇点,见文献[6-8].
2.2 带锥奇点的non-CSCHCMU度量的基本性质,football分解与粘合仍然假设M为紧黎曼面,p1,p2,…,pN为M上N个点,g为 M\{p1,p2,…,pN}上光滑保角度量.设(U,z)为M\{p1,p2,…,pN}上的局部复 坐标系,则g在U上可写成
| $g={{e}^{2\varphi }}|dz{{|}^{2}},$ |
于是高斯曲率K=-e-2φΔφ,这里
| $\nabla K=\sqrt{-1}{{e}^{-2\varphi }}{{K}_{{\bar{z}}}}\frac{\partial }{\partial \bar{z}}$ |
为M\{p1,p2,…,pN}上 的全纯向量场,这也等价于
| $V=\frac{1}{2}\left( \sqrt{-1}{{e}^{-2\varphi }}{{K}_{{\bar{z}}}}\frac{\partial }{\partial z}-\sqrt{-1}{{e}^{-2\varphi }}{{K}_{z}}\frac{\partial }{\partial \bar{z}} \right)$ |
为M\{p1,p2,…,pN}上的Killing 向量场.进一步,如果g是non-CSC HCMU度量,∇K和V都是非平凡的.
现在假设g为non-CSC HCMU度量,p1,p2,…,pN为g的锥奇点,并且g在p1,p2,…,pN处分别有锥角度2πα1,2πα2,…,2παN,这里α1,α2,…,αN都为正实数并且都不为1,因为文献[9]证明了如果HCMU度量在某点处的锥角度为2π,则度量在该点处光滑,即该点实际上不是度量的奇点.Chen[3]通过研究V以及V的积分曲线得到如下重要结论:
命题2.1(文献[3]) 高斯曲率K可以连续地延拓到整个M上.
命题2.2(文献[3]) V的奇点数有限,并且V的奇点集一定是K的鞍点集和K的局部极值点集的并集,这里K的鞍点是指存在两条以上V的积分曲线在该点相交.
命题2.3(文献[3]) K的鞍点必为g的锥奇点,并且K的鞍点锥角度为2πα形式,这里α为整数,进一步V在K的鞍点处的旋转指标为α-1.
命题2.4(文献[3]) g的锥奇点除了K的鞍点外,都是K的局部极值点.K的光滑临界点都是局部极值点,即K的局部极值点分成2类:一类是g的除鞍点外的锥奇点,另一类是K的全部光滑临界点.V在K的任何一个局部极值点处的旋转指标都是1.
定理2.1(文献[3]) 设{p1,p2,…,pI}⊂{p1,p2,…,pN}为K鞍点集,则M的欧拉示性数为
| $\chi \left( M \right)=\sum\limits_{i=1}^{I}{({{\alpha }_{i}}-1)+\left( N-I \right)+S,}$ | (6) |
这里S表示K的光滑临界点个数.
注:定理2.1是将Poincaré-Hopf定理应用到V上并且结合命题2.2,2.3和2.4得到的.
由定理2.1,可以得到如果K没有鞍点,χ(M)=N+S >0,因此,M为球面,并且N+S=2,即K 只有2个局部极值点分别在K的 最大、最小值点处.这种HCMU度量实际上是旋转对称的,称为football,如图 1所示.
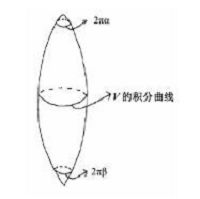
|
Download:
|
| 图 1 Football Fig. 1 Football | |
这里南北极分别是K的最小、最大值点,并且度量在两点处的锥角度分别为2πβ、2πα,α>β,纬线为V的积分曲线.具体地,g=du2+f(u)2dθ2(0≤u≤l,0≤θ≤2π),这里f(u)满足基本性质:f(0)=f(l)=0;f ′(0)=α,f′(l)=-β;f(u)>0,u∈(0,l).由于g为HCMU度量,f还要满足其他性质,关于football 的详细描述见文献[4].为了方便,记这样的football为S{α,β}2.此外,文献[3]还给出了利用football构造复杂一些non-CSC HCMU度量的方法,例如:取2个相同的football,

|
Download:
|
| 图 2 2个football粘合 Fig. 2 Gluing of two footballs | |
命题2.5(文献[4]) 带锥奇点的non-CSC HCMU度量,任何K的局部极值点都是K的最大或最小值点.如果记K1、K2为K的最大最小值,则K1 >0,K1>K2>-(K1+K2).
定理2.2(文献[4]) 带锥奇点的non-CSC HCMU度量都可以沿着有限条从K的最大值点到K的最小值点的测地线(这些测地线与V垂直)将底流形剖分成有限多片,而每一片都与某个football等距.
定理2.3(文献[4]) 两个football S{α1,β1}2与S{α2,β2}2能沿着经线或经线的一段粘起来的充要条件是:
| $\frac{{{\alpha }_{1}}}{{{\beta }_{1}}}=\frac{{{\alpha }_{2}}}{{{\beta }_{2}}},\frac{{{\alpha }_{1}}}{{{\alpha }_{2}}}=\frac{{{A}_{1}}}{{{A}_{2}}},$ |
这里A1、A2分别表示S{α1,β1}2和S{α2,β2}2 的面积.
2.3 特征1-形式与non-CSCHCMU度量 2.3.1 带锥奇点的non-CSC HCMU度量文献[5]用复分析的方法研究了带锥奇点的non-CSC HCMU度量.具体地,其定义了∇K的对偶1-形式,称为特征1-形式. 证明了特征1-形式为亚纯1-形式,研究了特征1-形式在奇点处的阶以及留数性质,并且利用特征1-形式构造出了non-CSC HCMU度量.
仍沿用之前的记号,令M是紧黎曼面,p1,p2,…,pN为M上N个点,g为M 上的non-CSC HCMU度量,在p1,p2,…,pN处有锥奇点并且有锥角度2πα1,2πα2,…,2παN.又设{p1,p2,…,pI}{p1,p2,…,pN} 为K的鞍点,{pI+1,pI+2,…,pJ}{p1,p2,…,pN}为K的最大值点,{pJ+1,pJ+2,…,pN}{p1,p2,…,pN}为K 的最小值点. 再设 {q1,q2,…,qS}M\{p1,p2,…,pN} 为K的光滑极值点,其中q1,q2,…,qT 为K的最大值点,qT+1,qT+2,…,qS为K的最小值点.则∇K在 M\{p1,p2,…,pN,q1,q2,…,qS} 上处处非零,于是定义ω为∇K的对偶1-形式,具体地,令ω为M\{p1,p2,…,pN,q1,q2,…,qS}上的全纯1-形式且 ω(∇K)=-14 (这里-14是技术性常数),称ω为g的特征1-形式.于是有下列结果:
定理2.4(文献[5]) ω为M上亚纯1-形式.p1,p2,…,pI为ω的零点并且ω在pi,i=1,2,…,I处的阶为αi-1.pI+1,pI+2,…,pN,q1,q2,…,qS都是ω的单极点.
定理2.5(文献[5]) 1)在M\{p1,p2,…,pN,q1,q2,…,qS}上有,
| $K=(-\frac{{{K}^{3}}}{3}+CK+C\prime )\omega ,$ | (7) |
这里C是(2)式中常数,C′是实常数.
2) 在M\\{p1,p2,…,pN,q1,q2,…,qS}上有
| $g=4(-\frac{{{K}^{3}}}{3}+CK+C\prime )\omega \bar{\omega }.$ | (8) |
| $3)-\frac{{{K}^{3}}}{3}+CK+C\prime =-\frac{1}{3}(K-{{K}_{1}})(K-{{K}_{2}})(K+{{K}_{1}}+{{K}_{2}}),$ | (9) |
这里K1、K2分别为K的最大最小值.
定理2.6(文献[5]) 令αmax=αI+1+αI+2+…+αJ+T,αmin=αJ+1+αJ+2+…+αN+S-T,
注:由于文献[9]证明了如果HCMU度量在某点处的锥角度为2π,则度量在该点处光滑.因此,可以把K的光滑极值点看成锥角度为2π的锥奇点.在这种观点下,
文献[6]将文献[5]的结果推广到了既带锥奇点又带cusp奇点的non-CSC HCMU度量上.具体地,令M为紧 黎曼面,p1,p2,…,pN为M上N个点,设g为M上non-CSC HCMU 度量,p1,p2,…,pL(0 <L≤N) 为g的cusp奇点,pL+1,pL+2,…,pN为g的锥奇点并且分别有锥角度2παL+1,2παL+2,…,2παN.则有下列结论:
命题2.6(文献[6]) 高斯曲率K为M上的连续函数.
命题2.7(文献[6]) 存在实常数C′使得在M\{p1,p2,…,pN}上,
| $-4\sqrt{-1}\nabla K\left( K \right)=-\frac{{{K}^{3}}}{3}+CK+C\prime .$ |
命题 2.8(文献[6]) K的光滑极值点数有限.
由命题2.8,设q1,q2,…,qS 为K的所有光滑极值点.于是∇K为 M\{p1,p2,…,pN,q1,q2,…,qS} 上处处非零的全纯向量场.因此,可以像在2.3.1中那样定义∇K的对偶1-形式ω,ω(∇K)=
定理 2.7(文献[6]) ω为M上亚纯1-形式,在M\{p1,p2,…,pN,q1,q2,…,qS} 上有:
| $1)\partial K=(-\frac{{{K}^{3}}}{3}+CK+C\prime )\omega ,$ |
| $2)g=(-\frac{{{K}^{3}}}{3}+CK+C\prime )\omega \bar{\omega }.$ |
定理 2.8(文献[6]) 存在μ <0,使得
| $-\frac{{{K}^{3}}}{3}+CK+C\prime =-\frac{1}{3}{{\left( K-\mu \right)}^{2}}\left( K+2\mu \right).$ |
进一步,在M\{p1,p2,…,pN,q1,q2,…,qS} 上,μ <K<-2μ.
定理2.9(文献[6]) g的cusp奇点都是ω的单极点,并且ω在该极点处有正留数.在K的光滑极值点q1,q2,…,qS处,K的 取值都是-2μ,并且ω在每个K的光滑极值点处的留数都是
定理2.10(文献[6]) 每个g的锥奇点或者是ω的零点或者是ω的单极点,不妨设pL+1,pL+2,…,pL+I为ω的零点,pL+I+1,pL+I+2,…,pN为ω的单极点.则αi,i=L+1,L+2,…,L+I,为整数,ω在 pi处的阶为αi-1,K可以光滑延拓到pi处,
在定理1.1的证明中,必要性的证明比较容易,充分性的证明主要是将文献[3]中构造non-CSC HCMU度量的方法推广.
定理1.1的证明 (必要性)设S2上存在以p1,p2,p3为锥奇点的non-CSC HCMU度量g,并且g在p1,p2,p3处的锥角度分别为 2πα1,2πα2,2πα3.如果α1,α2,α3中没有整数,由命题2.3,K没有鞍点,又由定理2.1,g为 football.再由定理2.1,公式(6)成立,而公式(6)左边为2,右边为3+S≥3,矛盾.因此,α1,α2,α3 中必有整数.
(充分性)如果α1,α2,α3中有整数,不妨设α1为整数.则α1-1≥1,并且α1-1+α2>α3或者 α1-1+α3>α2,不妨假设前者成立.令
| $\frac{{{S}^{2}}{{_{\{\alpha }}_{2}}{{,}_{\rho {{\alpha }_{2}}}}_{\}}的面积}{{{S}^{2}}_{\{1,\rho \}}的面积}={{\alpha }_{2}},$ |
于是由定理2.3,S{α2,ρα2}2和 S{1,ρ}2 能沿经线或经线的一段光滑粘起来.取S{α2,ρα2}2和一个S{1,ρ}2,如同上文中文献[3] 中构造的那样,先将S{α2,ρα2}2和S{1,ρ}2从K的最小值点沿着经线剪开相同的长度,再将S{α2,ρα2}2剪开后的经线与S{1,ρ}2剪开后的经线相应地粘在一起,于是 得到一个新的non-CSC HCMU度量有锥角度2πα2,4π,2π(ρα2+ρ). 再取一个S{1,ρ}2,也从K的最小值点沿着经线剪开与前面相同的长度,将 上一步中,粘在一起的两条经线中的一段再剪开,与新的S{1,ρ}2中被剪开的经线再相应地粘在一起,于是又得到一个新的non-CSC HCMU度量,有锥角度2πα2,6π,2π(ρα2+2ρ).然后重复上述步骤,直到把所有S{1,ρ}2用完,最终得到一个non-CSC HCMU度量,有锥角度2πα2,2πα1,2π[ρα2+(α1-1)ρ],而由ρ的定义,ρα2+(α1-1)ρ=α3.因此,最终得到一个non-CSC HCMU度量,有预先指定的锥角度,并且底流形是球面.将这个non-CSC HCMU度量记为g,底流形记为M,则存在f:S2→M为双全纯映射.于是拉回度量f*g为S2上的non-CSC HCMU度量,设f*g的奇点为q1,q2,q3,则存在Mbius 变换σ:S2→S2使得σ(p1)=q1,σ(p2)=q2,σ(p3)=q3. 于是σ*f*g为S2上的non-CSC HCMU度量并且以p1,p2,p3为锥奇点.由于σ和f都是双全纯变换,p1,p2,p3处的锥角度分别为2πα1,2πα2,2πα3.证毕.
4 定理1.2的证明由于带锥奇点的non-CSC HCMU度量与既带锥奇点又带cusp奇点的non-CSC HCMU度量很相似,这里只计算带锥奇点的non-CSC HCMU度量的第n个能量积分.
定理1.2的证明 首先不妨设{p1,p2,…,pI}⊂{p1,p2,…,pN}为K的鞍点集.由定理2.5,在M′上,
| $g=-\frac{4}{3}(K-{{K}_{1}})(K-{{K}_{2}})(K+{{K}_{1}}+{{K}_{2}})\omega \bar{\omega }$ |
以及
| $dK=-\frac{1}{3}(K-{{K}_{1}})(K-{{K}_{2}})(K+{{K}_{1}}+{{K}_{2}})\left( \omega +\bar{\omega } \right).$ |
因此,在M′上
| ${{K}^{n}}dg=\frac{\sqrt{-1}}{2}{{K}^{n}}[-\frac{4}{3}(K-{{K}_{1}})(K-{{K}_{2}}),$ |
| $(K+{{K}_{1}}+{{K}_{2}})]\omega \wedge \bar{\omega }.=\frac{\sqrt{-1}}{2}4{{K}^{n}}dK\wedge \bar{\omega }=\frac{\sqrt{-1}}{2}\frac{4}{n+1}d({{K}^{n+1}}\omega -).$ |
于是
| ${{C}_{n}}\left( g \right)={{\int }_{M}}\prime {{K}^{n}}dg=\frac{\sqrt{-1}}{2}n+1{{\int }_{M}}\prime d({{K}^{n+1}}\bar{\omega })=\frac{2\sqrt{-1}}{n+1}\underset{\in \to 0}{\mathop{lim}}\,{{\int }_{M\backslash (\cup }}{{^{N}}_{k=1}}{{_{{{D}_{\in }}({{p}_{k}})\cup {{\cup }^{S}}_{j=1}{{D}_{\in }}({{q}_{j}}))}}^{d({{K}^{n+1}}\omega -),}}$ |
这里D∈(pk)(D(qj))表示以pk(qj)为圆心半径为∈的坐标圆盘.由Stokes公式,
| ${{\int }_{M\backslash \in (\cup }}{{^{N}}_{k=1}}{{_{D({{p}_{k}})\cup {{\cup }^{S}}_{j=1}{{D}_{\in }}({{q}_{j}}))}}^{d({{K}^{n+1}}\omega -)}}=-\underset{k=1}{\overset{N}{\mathop{\sum }}}\,{{\int }_{\partial D}}{{_{\in }}_{({{p}_{k}})}}{{K}^{n+1}}\bar{\omega }-\underset{j=1}{\overset{S}{\mathop{\sum }}}\,{{\int }_{\partial D}}{{_{\in }}_{({{p}_{j}})}}{{K}^{n+1}}\bar{\omega }.$ |
由于p1,p2,…,pI为ω的零点,
| $\underset{\in \to 0}{\mathop{lim}}\,{{\int }_{\partial D}}{{_{\in }}_{({{p}_{i}})}}{{K}^{n+1}}\bar{\omega }=0,i=1,2,\ldots ,I,$ |
而
| $\underset{\in \to 0}{\mathop{lim}}\,{{\int }_{\partial D}}{{_{\in }}_{({{p}_{l}})}}{{K}^{n+1}}\bar{\omega }=(-2\pi \sqrt{-1})Re{{s}_{p}}_{l}\left( \omega \right){{(K({{p}_{l}}))}^{n+1}},l=I+1,I+2,\ldots ,N,$ |
类似地,
| $\underset{\in \to 0}{\mathop{lim}}\,{{\int }_{\partial D}}{{_{\in }}_{({{q}_{j}})}}{{K}^{n+1}}\bar{\omega }=(-2\pi \sqrt{-1})Re{{s}_{q}}_{j}\left( \omega \right){{(K({{q}_{j}}))}^{n+1}},j=1,2,\ldots ,S.$ |
由定理2.6,如果pl,l=I+1,I+2,…,N,为K的最大值点,则
| $K({{p}_{l}})={{K}_{1}},Re{{s}_{p}}_{l}\left( \omega \right)=-\frac{3{{\alpha }_{l}}}{({{K}_{1}}-{{K}_{2}})({{K}_{2}}+2{{K}_{1}})};$ |
如果pl为K的最小值点,则
| $K({{p}_{l}})={{K}_{2}},Re{{s}_{p}}_{l}\left( \omega \right)=\frac{{{{\tilde{\alpha }}}_{max}}}{{{{\tilde{\alpha }}}_{min}}}\frac{3{{\alpha }_{l}}}{({{K}_{1}}-{{K}_{2}})({{K}_{2}}+2{{K}_{1}})};$ |
如果qj,j=1,2,…,S,为K的最大值点,则
| $K({{q}_{j}})={{K}_{1}},Re{{s}_{q}}_{j}\left( \omega \right)=-\frac{3}{({{K}_{1}}-{{K}_{2}})({{K}_{2}}+2{{K}_{1}})};$ |
如果qj为K的最小值点,则
| $K({{q}_{j}})={{K}_{2}},Re{{s}_{q}}_{j}\left( \omega \right)=\frac{{{{\tilde{\alpha }}}_{max}}}{{{{\tilde{\alpha }}}_{min}}}\frac{3}{({{K}_{1}}-{{K}_{2}})({{K}_{2}}+2{{K}_{1}})}.$ |
因此,
| $\begin{align} & \underset{\in \to 0}{\mathop{lim}}\,(-\underset{k=1}{\overset{N}{\mathop{\sum }}}\,{{\int }_{\partial D}}{{_{\in }}_{({{p}_{k}})}}{{K}^{n+1}}\bar{\omega }-\underset{j=1}{\overset{S}{\mathop{\sum }}}\,{{\int }_{\partial D}}{{_{\in }}_{({{p}_{j}})}}{{K}^{n+1}}\bar{\omega })= \\ & \frac{2\pi \sqrt{-}1\left( -3 \right){{K}^{n+1}}_{1}{{{\tilde{\alpha }}}_{max}}}{({{K}_{1}}-{{K}_{2}})({{K}_{2}}+2{{K}_{1}})}+\frac{2\pi \sqrt{-1}\text{ }3{{K}^{n+1}}_{2}}{({{K}_{1}}-{{K}_{2}})({{K}_{2}}+2{{K}_{1}})}\frac{{{{\tilde{\alpha }}}_{max}}}{{{{\tilde{\alpha }}}_{min}}}{{{\tilde{\alpha }}}_{min}} \\ & =\frac{3\sqrt{-1}({{K}^{n+1}}_{2}-{{K}^{n+1}}_{1}){{\alpha }_{max}}}{({{K}_{1}}-{{K}_{2}})({{K}_{2}}+2{{K}_{1}})}, \\ \end{align}$ |
这里αmax=2παmax.因此,
| ${{C}_{n}}\left( g \right)=\frac{6{{\alpha }_{max~}}({{K}^{n+1}}_{1}-{{K}^{n+1}}_{2})}{\left( n+1 \right)({{K}_{1}}-{{K}_{2}})({{K}_{2}}+2{{K}_{1}})}.$ |
证毕.
| [1] | Calabi E. Extremal Kähler metrics [C]//Seminar on differential geometry. Ann of Math Stud 102, Princeton: Princeton Univ. Press, 1982: 259-290. |
| [2] | Chen X X. Extremal Hermitian metrics on Riemann surfaces[J]. Calc Var , 1999, 8 :191–232. DOI:10.1007/s005260050123 |
| [3] | Chen X X. Obstruction to the existence of metric whose curvature has umbilical Hessian in a K-surface[J]. Communications in Analysis and Geometry , 2000, 8 (2) :267–299. DOI:10.4310/CAG.2000.v8.n2.a2 |
| [4] | Chen Q, Chen X X, Wu Y Y. The structure of HCMU metric in a K-surface[J]. International Mathematics Research Notices , 2005, 16 :941–958. |
| [5] | Chen Q, Wu Y Y. Character 1-form and the existence of an HCMU metric[J]. Math Ann , 2011, 351 (2) :327–345. DOI:10.1007/s00208-010-0598-z |
| [6] | Chen Q, Wu Y Y, Xu B. On one-dimensional and singular Calabi's extremal metrics whose Gauss curvatures have nonzero umbilical Hessians[J]. Israel Journal of Mathematics , 2015, 208 (1) :385–412. DOI:10.1007/s11856-015-1204-6 |
| [7] | Chen X X. Weak limits of Riemannian metrics in surfaces with integral curvature bound[J]. Calc Var , 1998, 6 :189–226. DOI:10.1007/s005260050089 |
| [8] | Wang G F, Zhu X H. Extremal Hermitian metrics on Riemann surfaces with singularities[J]. Duke Math Journal , 2000, 104 (2) :181–210. DOI:10.1215/S0012-7094-00-10421-8 |
| [9] | Lin C S, Zhu X H. Explicit construction of extremal Hermitian metric with finite conical singularities onS2[J]. Communications in Analysis and Geometry , 2002, 10 (1) :177–216. DOI:10.4310/CAG.2002.v10.n1.a8 |
 2016, Vol. 33
2016, Vol. 33 


