监督学习中的许多问题都可以归结为如下的有限和问题
| $ \min f({\boldsymbol{x}})=\frac{1}{n} \sum\limits_{i=1}^n f_i({\boldsymbol{x}}). $ | (1) |
其中: n是样本个数, 每个fi:
如果忽视问题(1)的有限和结构, 可以对其直接运用传统的优化方法, 比如梯度下降法
| $ {\boldsymbol{x}}_{k+1}={\boldsymbol{x}}_k-\eta \nabla f\left({\boldsymbol{x}}_k\right). $ | (2) |
其中: η是步长, ▽f(xk)是f在xk处的梯度。但在机器学习背景下, 样本数量n常常是上万甚至十万或百万级的, 而计算全梯度▽f(xk)要求计算n个fi的梯度, 由此带来的计算量是巨大的, 其他基于全梯度的传统优化方法也面临同样的问题。
为解决上述问题, 基于Robbins与Monro[1]对随机近似的开创性工作, 研究者们[2-4]提出并发展了随机梯度下降(stochastic gradient descent, SGD)。SGD利用问题(1)的有限和结构, 在其最简单的形式下, 算法等可能地随机抽取单个样本i并进行如下的更新
| $ {\boldsymbol{x}}_{k+1}={\boldsymbol{x}}_k-\eta \nabla f_i\left({\boldsymbol{x}}_k\right). $ | (3) |
其中▽fi(xk)是fi在xk处的梯度。该策略极大降低了每次更新所需要的计算量, 因而在许多具有低精度要求的机器学习问题中成为主流方法, 在无约束有限和问题之外的其他问题(比如带大量凸约束的随机优化问题[5])中也有广泛的应用。但是当精度要求较高时, SGD的方向方差不能随迭代递减的缺点使其即使在光滑强凸的问题里也只能具有次线性的收敛速度[6]。
为减小SGD的方向方差从而提高其收敛速度, 近年来随机方差缩减类方法被提出并得到一定的关注与发展。方差缩减方法通过利用之前迭代中的历史梯度信息, 以相比于SGD更多的内存或者计算开销为主要代价, 得到对当前梯度的更好估计, 该类估计的均方误差能够随着迭代进行而逐渐减小。
最早的方差缩减方法是随机平均梯度算法[7-8], 它利用存储的历史梯度信息构造随机平均梯度估计子, 开创了随机方差缩减方法的研究。与之类似,以较大内存开销为主要代价的算法还包括SAGA[9]、k-SVRG[10]、SARGE[11]等。另一类方差缩减方法以更大的计算开销为提高收敛速度的主要代价, 比如SVRG[12]、S2GD[13]、L-SVRG[14]、SCSG[15]、VR-SGD[16]、SARAH[17]等, 以上算法均实现了在强凸时的线性收敛。
在这些方差缩减方法的基础上, 人们从不同的改进角度出发做了多方面的工作。一些工作应用重要性采样技术或者随机洗牌技术, 如Prox-SVRG[18]、PVRSG[19]、SAGA with random reshuffling[20]等; 一些工作尝试进一步加快收敛, 如Katyusha[21]、MiG[22]、RPDG[23]等; 一些工作结合自适应步长以减少调参负担, 如SVRG-BB[24]、Ada-SVRG[25]、AI-SARAH[26]、SARAH-AS[27]等。关于结合了BB(Barzilai-Borwein, BB)步长的方法, 将在下一节做更详细的介绍。
1 相关工作1988年Barzilai和Borwein[28]提出BB方法, 用于为梯度类方法计算步长。其核心思想类似于拟牛顿法, 将梯度下降法迭代式(2)中的步长η等价地看作一个数量矩阵ηI(其中I是单位矩阵), 令ηI使割线方程的残差的模长最小化而解出合适的η值, 相应的ηI因此是目标函数在当前迭代点处Hessian矩阵之逆的一个较好近似。具体地, η应满足下列2个方程之一:
| $ \min \left\|\eta^{-1} {\boldsymbol{s}}_{k-1}-{\boldsymbol{G}}_{k-1}\right\|, $ | (4) |
| $ \min \left\|{\boldsymbol{s}}_{k-1}-\eta {\boldsymbol{G}}_{k-1}\right\|. $ | (5) |
其中: sk-1= xk- xk-1, Gk-1= ▽f(xk)- ▽f(xk-1)。由此解得的η值分别是
| $ {\boldsymbol{\eta}}_k^{{\mathrm{BB}} 1} =\frac{{\boldsymbol{s}}_{k-1}^{{\mathrm{T}}} {\boldsymbol{s}}_{k-1}}{{\boldsymbol{s}}_{k-1}^{{\mathrm{T}}} {\boldsymbol{G}}_{k-1}} , $ | (6) |
| $ {\boldsymbol{\eta}}_k^{{\mathrm{BB}} 2} =\frac{{\boldsymbol{s}}_{k-1}^{{\mathrm{T}}} {\boldsymbol{G}}_{k-1}}{{\boldsymbol{G}}_{k-1}^{{\mathrm{T}}} {\boldsymbol{G}}_{k-1}}. $ | (7) |
其中前一种BB步长得到了更广泛的使用。
观察上述式子, 注意Gk-1用到2个相邻迭代点处的全梯度▽f(xk)和▽f(xk-1),由引言中的讨论可知这在大规模机器学习问题中通常将带来极大的计算负担。在著名的SVRG算法[12]中, 研究者设计了双循环结构, 全梯度仅在外循环的“快照”点(也称为全梯度点, 下文通常记为
算法0 SVRG-BB算法[24]
参数: 内循环长度m, 初始点
for k=0, 1, … do
if k>0 then
end if
选取x0=
for t=0, 1, …, m-1 do
随机选取it∈{1, …, n}
gt=▽fit(xt)-▽fit(
xt+1=xt-ηkgt
end for
选取
end for
在SVRG-BB提出之后, 也有一些工作将BB方法或者其改进运用到方差缩减方法里。例如, Yang等[29]与Yu等[30]将基于非精确梯度的随机BB方法与方差缩减方法相结合, 分别得到MB-SARAH-RBB算法和mS2GD-RBB算法; Yu等[31]将对角BB方法与方差缩减方法相结合, 得到VM-mSRGBB算法; Xie等[32]针对方差缩减算法SAGA[9]的特点, 对BB方法发展了新的变体并将其与SAGA结合, 得到一个支持非欧范数的新算法, 等等。
2 直观动机对于采用了一定自适应步长的算法, 人们总希望通过其他方面的改进提升算法的表现。注意到SVRG-BB虽然具有良好的数值效果, 但是与最优固定步长①下的SVRG算法相比, 仍有进步的空间。针对SVRG-BB的数值效果劣于SVRG这一现象, 提出如下的直观解释: 由于SVRG-BB所使用的BB步长本质上基于对当前外循环快照点的局部二阶信息的逼近, 所以其效果在当前快照处应是最优的, 而随着内循环迭代的进行, 迭代点离快照越来越远, 使得仍用作迭代步长的BB步长逐渐“过时”与失效, 最终(部分地)导致SVRG-BB的效果与SVRG相比较差。
① 指在采用固定步长的SVRG的数值实验中, 在一定的外循环数下使得其最终优化间隙最小的固定步长。
图 1说明了SVRG-BB可能存在的问题。图中绿色圆点表示当前外循环所使用的快照

|
Download:
|
| 图 1 对直观解释的图示 Fig. 1 Illustration for the intuitive explanation | |
总之, 我们认为SVRG-BB算法里存在一个“进展-自适应步长有效性”的权衡, 其本质上是“进展幅度-进展质量”的权衡, 即: 当算法取得较大的进展, 内循环迭代点距离当前快照越来越远, 此时自适应步长越来越“过时”, 导致接下来进展的质量变差; 当算法进展较小时, 自适应步长更有效, 算法的进展质量更高。所以希望能在进展幅度与进展质量之间寻求一个更好的平衡。具体地, 我们提出将Katyusha动量加入SVRG-BB以寻求该平衡。
Katyusha动量由Allen-Zhu[21]于2016年提出, 成功解决了SVRG在结合Nesterov动量时效果不佳的问题。相应的Katyusha算法是针对带凸正则项的问题(1)的达到最优加速收敛速率且在并行化中具有最优线性加速的方法,对其后的加速方差缩减方法的研究产生了相当的影响。在其最简单的形式下, Katyusha算法内循环中的关键迭代步骤如下:
| $ \begin{aligned} & {\boldsymbol{y}}_{t+1} \leftarrow \tau_1 z_t+\tau_2 \tilde{{\boldsymbol{x}}}+\left(1-\tau_1-\tau_2\right) {\boldsymbol{x}}_t , \\ & {\boldsymbol{g}}_{t+1} \leftarrow \nabla f(\tilde{{\boldsymbol{x}}})+\nabla f_{i_{t+1}}\left({\boldsymbol{y}}_{t+1}\right)-\nabla f_{i_{t+1}}(\tilde{{\boldsymbol{x}}}), \\ & {\boldsymbol{x}}_{t+1} \leftarrow {\boldsymbol{y}}_{t+1}-\frac{1}{3 L} {\boldsymbol{g}}_{t+1} , \\ & {\boldsymbol{z}}_{t+1} \leftarrow {\boldsymbol{z}}_t-\frac{1}{3 \tau_1 L} {\boldsymbol{g}}_{t+1}. \end{aligned} $ |
其中:τ1, τ2∈(0, 1)是动量系数, it+1是取值于{1, 2, …, n}的一个随机变量;
如果动量系数τ1=τ2=0,则相应的迭代实质上退化成SVRG算法的仅有一个序列(即x序列)的迭代形式; 如果仅τ2=0,则可理解为对SVRG算法直接使用一定形式的Nesterov加速技巧, 但这么做得到的理论结果和实际效果都是欠佳的。对此Allen-Zhu提出, 由于随机方差缩减方法中所使用的方向仅是相应真实梯度方向的一个估计, 故一旦产生了一个不良的估计, 其影响将在后续通过辅助序列z与y持续存在, 破坏算法的效果。因此Allen-Zhu向y序列进一步加入了“快照”
易见, 若将Katyusha动量加入SVRG-BB, 则当Katyusha动量前的系数较大时, 所得算法将更倾向于停留在当前快照
就迭代形式而言, 基于上述直观动机, 在将前述迭代机制结合进SVRG-BB之前, 对Katyusha算法内循环的关键步骤大致做出如下改变: 由于不考虑加入传统加速方法中的动量, 所以迭代中不使用和更新前述步骤里的辅助序列z且设定系数τ1=0。保留辅助序列y(此时它仅是主序列x和快照
算法1 SVRG-BB-Katyusha算法
参数: 内循环长度m, 初始点
for k=0, 1, … do
if k>0 then
end if
选取x0=
for t=0, 1, …, m-1 do
yt=θxt+(1-θ)
随机选取it∈{1, …, n}
gt=▽fit(yt)-▽fit(
end for
选取
end for
将动量加入自适应步长方法以提高后者的表现并不是一个新鲜的做法。比如Kingma与Ba[33]将动量与RMSprop算法结合而得到ADAM算法等。这类已有的工作虽然取得了很好的效果, 却往往缺乏如下意义上的直观解释, 即难以理解为什么是这一特别的动量与这一特别的自适应步长相结合, 能够获得比其他可能的结合更好的效果。而在SVRG-BB这一基于快照点局部信息的自适应步长算法与Katyusha动量之间进行的结合, 更充分地体现和利用了两者各自的特点, 具有较明确的直观解释和一定的启发性, 指出了将Katyusha动量与其他基于快照局部信息的自适应步长方法结合可能获得额外好处(即增加自适应步长的有效性), 拓展了对Katyusha动量作用的认识。
本文工作主要有以下几方面:
1) 指出SVRG-BB的算法设计带来了“进展-自适应步长有效性”的权衡问题, 为该算法的改进提供了一个直观的视角和思路。
2) 结合已有的2种Katyusha动量的作用形式, 提出一种新的Katyusha动量作用形式, 并根据之前对SVRG-BB算法的直观分析与Katyusha动量的特点, 将其结合到SVRG-BB中得到SVRG-BB-Katyusha, 在强凸条件下给出其线性收敛性质的证明。随后基于“贪婪”思想, 提出SVRG-BB-Katyusha-SPARSE以尽可能减少带Katyusha动量的内循环迭代带来的额外计算。
3) 对所提出的SVRG-BB-Katyusha和SVRG-BB-Katyusha-SPARSE进行求解逻辑回归问题的数值实验。实验结果表明, 所提出算法的实际表现在如下意义上领先于SVRG-BB, 即在达到一定外循环数时优化间隙有若干个数量级的减小。
3 SVRG-BB-Katyusha算法下面正式引入基于上述直观思想改进后的算法, 并称之为SVRG-BB-Katyusha(算法1)。
做如下几点说明:其一, 为突出所引入Katyusha动量的作用, 算法1保持了SVRG-BB的其他设计(如快照的选择方式, 下一个外循环初始点的选择方式等)不变; 其二, Katyusha动量在不同的算法中可以有不同的形式, 我们主要参考并结合了L-Katyusha[14]以及MiG[22]的设计, 得到新的形式并将其结合到SVRG-BB之中;其三, 在数值实验中总设定动量控制系数θ=0.9,以此免去对该参数进行精调的负担并取得良好效果;其四, 在
回顾引入Katyusha动量的直观思想, 即利用Katyusha动量的“拉回”作用, 将迭代点不断拉回快照从而使得BB步长免于“过时”。据此提出, 在每一次内循环中都执行带Katyusha动量的迭代或许是不必要的, 只要足够频繁地执行带Katyusha动量的迭代而保持其余的内循环迭代与SVRG-BB相同, 使得内循环迭代点与快照足够近, 就可能保持由更有效的BB步长带来的效果增益, 并规避一部分由更复杂的内循环迭代方式带来的额外计算。基于此, 提出以下的SVRG-BB-Katyusha-SPARSE(算法2)。
算法2 SVRG-BB-Katyusha-SPARSE算法
参数: 内循环长度m, 初始点
for k=0, 1, … do
if k>0 then
end if
选取x0=
for t=0, …, m-1 do
if t mod m0≠0 then
随机选取it∈{1, 2,…, n}
xt+1=xt-ηk(▽fit(xt)-▽fit(
else
yt=θxt+(1-θ)
随机选取it∈{1, 2,…, n}
gt=▽fit(yt)-▽fit(
end if
end for
选取
end for
基于“贪婪”思想, 在能够保证算法效果的情况下, 希望将参数m0取得尽可能大, 以尽可能减少带Katyusha动量的内循环迭代带来的额外计算负担。在数值实验中总选取m0=4,以此免去对该参数进行精调的负担并取得了良好效果。数值实验效果显示了这个算法的有效性, 但是理论性质还没有得到更多的刻画。
4 符号说明与假设在进行SVRG-BB-Katyusha的收敛性证明之前, 对证明中使用的符号说明如下: ‖x‖表示向量x的欧氏范数, 〈 a, b 〉表示向量a与向量b的内积, [n]={1, 2, …, n}表示如前的n个正整数构成的集合,
下面明确地列出对问题(1)所做的假设。
假设4.1 函数
| $ \begin{aligned} & f({\boldsymbol{y}}) \geqslant f({\boldsymbol{x}})+\langle\nabla f({\boldsymbol{x}}), {\boldsymbol{y}}-{\boldsymbol{x}}\rangle+\frac{\mu}{2}\|{\boldsymbol{y}}-{\boldsymbol{x}}\|^2, \\ & \forall {\boldsymbol{x}}, {\boldsymbol{y}} \in \mathbb{R}^d. \end{aligned} $ |
假设4.2 对所有i∈[n], 函数
| $ \begin{aligned} & f_i({\boldsymbol{y}}) \geqslant f_i({\boldsymbol{x}})+\left\langle\nabla f_i({\boldsymbol{x}}), {\boldsymbol{y}}-{\boldsymbol{x}}\right\rangle, \\ & \forall {\boldsymbol{x}}, {\boldsymbol{y}} \in \mathbb{R}^d. \end{aligned} $ |
假设4.3 对所有i∈[n], 函数
| $ \begin{aligned} f_i(\boldsymbol{y}) & \leqslant f_i(\boldsymbol{x})+\left\langle\nabla f_i(\boldsymbol{x}), \boldsymbol{y}-\boldsymbol{x}\right\rangle+\frac{L}{2}\|\boldsymbol{y}-\boldsymbol{x}\|^2, \\ \forall \boldsymbol{x}, \boldsymbol{y} & \in \mathbb{R}^d. \end{aligned} $ |
将假设4.3中的不等式对所有的i∈[n]求和并除以n,可知函数
下面给出SVRG-BB-Katyusha的收敛性证明, 首先介绍如下几个引理。
引理5.1及其证明基本复刻Kovalev等[14]的工作中的Lemma 4.2。由于定理5.1(收敛性定理)的证明主体是针对同一个外循环的, 其中步长保持不变, 于是在引理5.1中以η而非ηk代表步长, 这避免了诸如把χt(将在引理5.1中给出定义)记作χk, t的麻烦。在引理5.3中也类似地使用符号η。在之后的定理5.1中沿用η和χt的记法而不特别标记其所在的外循环, 对各迭代点列(除快照外)和收缩因子β(将在定理5.1中给出定义)也不特别标记其所在的外循环, 这对证明不产生影响。
引理5.1 定义
| $ \begin{aligned} & \left\langle {\boldsymbol{g}}_t, {\boldsymbol{x}}_*-{\boldsymbol{x}}_{t+1}\right\rangle+\frac{\mu}{2}\left\|{\boldsymbol{y}}_t-{\boldsymbol{x}}_*\right\|^2 \geqslant \\ & \frac{\alpha L}{2 \eta}\left\|{\boldsymbol{x}}_t-{\boldsymbol{x}}_{t+1}\right\|^2+\chi_{t+1}-\frac{1}{1+\eta \sigma} \chi_t. \end{aligned} $ | (8) |
证明 由
| $ \begin{aligned} \left\langle {\boldsymbol{g}}_t, {\boldsymbol{x}}_{t+1}-{\boldsymbol{x}}_*\right\rangle= & \mu\left\langle{\boldsymbol{y}}_t-{\boldsymbol{x}}_{t+1}, {\boldsymbol{x}}_{t+1}-{\boldsymbol{x}}_*\right\rangle+ \\ & \frac{\alpha L}{\eta}\left\langle{\boldsymbol{x}}_t-{\boldsymbol{x}}_{t+1}, {\boldsymbol{x}}_{t+1}-{\boldsymbol{x}}_*\right\rangle \\ = & \frac{\mu}{2}\left(\left\|{\boldsymbol{y}}_t-{\boldsymbol{x}}_*\right\|^2-\left\|{\boldsymbol{y}}_t-{\boldsymbol{x}}_{t+1}\right\|^2-\right. \\ & \left.\left\|{\boldsymbol{x}}_{t+1}-{\boldsymbol{x}}_*\right\|^2\right)+\frac{\alpha L}{2 \eta}\left(\left\|{\boldsymbol{x}}_t-{\boldsymbol{x}}_*\right\|^2-\right. \\ & \left.\left\|{\boldsymbol{x}}_t-{\boldsymbol{x}}_{t+1}\right\|^2-\left\|{\boldsymbol{x}}_{t+1}-{\boldsymbol{x}}_*\right\|^2\right) \\ \leqslant & \frac{\mu}{2}\left\|{\boldsymbol{y}}_t-{\boldsymbol{x}}_*\right\|^2+\frac{\alpha L}{2 \eta}\left(\left\|{\boldsymbol{x}}_t-{\boldsymbol{x}}_*\right\|^2-\right. \\ & \left.(1+\eta \sigma)\left\|{\boldsymbol{x}}_{t+1}-{\boldsymbol{x}}_*\right\|^2\right)- \\ & \frac{\alpha L}{2 \eta}\left\|{\boldsymbol{x}}_t-{\boldsymbol{x}}_{t+1}\right\|^2,\end{aligned} $ |
其中第2个等式利用了恒等式〈 a - b, b - c 〉=
引理5.2来自Johnson与Zhang[12]的工作, 对SVRG算法所使用的搜索方向的方差给出一个上界。
引理5.2 如下的不等式成立:
| $ \mathbb{E}\left\|{\boldsymbol{g}}_t\right\|^2 \leqslant 4 L\left(f\left({\boldsymbol{y}}_t\right)-f^*+f(\tilde{{\boldsymbol{x}}})-f^*\right),$ | (9) |
其中:gt=▽fit(yt)-▽fit(
下面是一个技术性引理, 在证明中起到重要作用。
引理5.3 如下的不等式成立:
| $ \begin{aligned} & \left\langle{\boldsymbol{g}}_t, {\boldsymbol{x}}_{t+1}-{\boldsymbol{x}}_t\right\rangle+\frac{\alpha L}{2 \eta}\left\|{\boldsymbol{x}}_t-{\boldsymbol{x}}_{t+1}\right\|^2 \geqslant \\ & \frac{1}{\theta}\left(f\left({\boldsymbol{y}}_{t+1}\right)-f\left({\boldsymbol{y}}_t\right)-\right. \\ & \left.\frac{\eta \theta}{2 L(\alpha-\eta \theta)}\left\|{\boldsymbol{g}}_t-\nabla f\left({\boldsymbol{y}}_t\right)\right\|^2\right) . \end{aligned} $ | (10) |
证明
| $ \begin{aligned} \left\langle{\boldsymbol{g}}_t, {\boldsymbol{x}}_{t+1}-{\boldsymbol{x}}_t\right\rangle+\frac{\alpha L}{2 \eta}\left\|{\boldsymbol{x}}_t-{\boldsymbol{x}}_{t+1}\right\|^2\\ = \frac{1}{\theta}\left(\frac{\alpha L}{2 \eta \theta}\left\|\theta\left({\boldsymbol{x}}_{t+1}-{\boldsymbol{x}}_t\right)\right\|^2+\left\langle{\boldsymbol{g}}_t, \theta\left({\boldsymbol{x}}_{t+1}-{\boldsymbol{x}}_t\right)\right\rangle\right) \\ = \frac{1}{\theta}\left(\frac{\alpha L}{2 \eta \theta}\left\|{\boldsymbol{y}}_{t+1}-{\boldsymbol{y}}_t\right\|^2+\left\langle\nabla f\left({\boldsymbol{y}}_t\right), {\boldsymbol{y}}_{t+1}-{\boldsymbol{y}}_t\right\rangle+\right. \\ \left.\left\langle{\boldsymbol{g}}_t-\nabla f\left({\boldsymbol{y}}_t\right), {\boldsymbol{y}}_{t+1}-{\boldsymbol{y}}_t\right\rangle\right) \\ = \frac{1}{\theta}\left(\frac{L}{2}\left\|{\boldsymbol{y}}_{t+1}-{\boldsymbol{y}}_t\right\|^2+\left\langle\nabla f\left({\boldsymbol{y}}_t\right), {\boldsymbol{y}}_{t+1}-{\boldsymbol{y}}_t\right\rangle+\right. \\ \frac{L}{2}\left(\frac{\alpha}{\eta \theta}-1\right)\left\|{\boldsymbol{y}}_{t+1}-{\boldsymbol{y}}_t\right\|^2+\left\langle{\boldsymbol{g}}_t-\nabla f\left({\boldsymbol{y}}_t\right), {\boldsymbol{y}}_{t+1}-\right. \\ \left.\left.{\boldsymbol{y}}_t\right\rangle\right) \geqslant \frac{1}{\theta}\left(f\left({\boldsymbol{y}}_{t+1}\right)-f\left({\boldsymbol{y}}_t\right)-\right.\\ \left.\frac{\eta \theta}{2 L(\alpha-\eta \theta)}\left\|{\boldsymbol{g}}_t-\nabla f\left({\boldsymbol{y}}_t\right)\right\|^2\right). \end{aligned} $ |
其中第2个等式利用了由算法1可推出的关系式yt+1- yt=θ(xt+1- xt),最后一个不等式利用了函数f的L-光滑性和Young不等式。
以下的引理给出对BB步长的上下界估计, 其证明可参考Tan等[24]的工作。
引理5.4 对于BB步长
| $ \frac{1}{m L} \leqslant \eta_k \leqslant \frac{1}{m \mu}, $ | (11) |
其中
证明 由f的L-光滑性得到下界, 由f的μ-强凸性得到上界。注意得到的上下界不依赖于k。
以下引理是Young不等式的一种变形。
引理5.5 对任意的a, b ∈
| $ \langle{\boldsymbol{a}}, {\boldsymbol{b}}\rangle \geqslant-\frac{\|{\boldsymbol{a}}\|^2}{2 \gamma}-\frac{\gamma\|{\boldsymbol{b}}\|^2}{2} . $ | (12) |
最终给出SVRG-BB-Katyusha的收敛性定理如下。
定理5.1 定义
| $ \begin{aligned} \beta \triangleq & \left(\frac{1}{1+\eta \sigma}\right)^m\left(1+\frac{\eta}{\alpha \theta(1+\eta \sigma)}\right)+ \\ & \frac{1}{\alpha \sigma}\left(\frac{1-\theta}{\theta}+\frac{2 \eta \theta}{\alpha-\eta \theta}\right). \end{aligned} $ |
则对任意α∈(0, 1], θ∈[θ0, 1), 当内循环长度m≥M时(M=M(α, θ)将在定理证明中给出), 有
| $ \mathbb{E}\left\|\tilde{{\boldsymbol{x}}}_l-{\boldsymbol{x}}_*\right\|^2 \leqslant\left(1-\frac{\delta^2}{6}\right)^l\left\|\tilde{{\boldsymbol{x}}}_0-{\boldsymbol{x}}_*\right\|^2, $ | (13) |
其中
证明 自此直至推导出后文的式(15)之前的部分称为证明的主体部分, 在该部分事先取定一个k∈{1, 2, …, l}并对第(k-1)个外循环进行分析。直至后文取全期望之前, 符号
| $ \begin{array}{l} f^* \geqslant f\left({\boldsymbol{y}}_t\right)+\left\langle\nabla f\left({\boldsymbol{y}}_t\right), {\boldsymbol{x}}_*-{\boldsymbol{y}}_t\right\rangle+\frac{\mu}{2}\left\|{\boldsymbol{y}}_t-{\boldsymbol{x}}_*\right\|^2 \\ = f\left({\boldsymbol{y}}_t\right)+\frac{\mu}{2}\left\|{\boldsymbol{y}}_t-{\boldsymbol{x}}_*\right\|^2+\left\langle\nabla f\left({\boldsymbol{y}}_t\right), {\boldsymbol{x}}_*-{\boldsymbol{x}}_t+\right. \\ \left.{\boldsymbol{x}}_t-{\boldsymbol{y}}_t\right\rangle \\ = f\left({\boldsymbol{y}}_t\right)+\frac{1-\theta}{\theta}\left\langle\nabla f\left({\boldsymbol{y}}_t\right), {\boldsymbol{y}}_t-\tilde{{\boldsymbol{x}}}_{k-1}\right\rangle+ \\ \frac{\mu}{2}\left\|{\boldsymbol{y}}_t-{\boldsymbol{x}}_*\right\|^2+\left\langle\nabla f\left({\boldsymbol{y}}_t\right), {\boldsymbol{x}}_*-{\boldsymbol{x}}_t\right\rangle \\ \geqslant f\left({\boldsymbol{y}}_t\right)+\frac{1-\theta}{\theta}\left(f\left({\boldsymbol{y}}_t\right)-f\left(\tilde{{\boldsymbol{x}}}_{k-1}\right)+\right. \\ \frac{\mu}{2}\left\|{\boldsymbol{y}}_t-\tilde{{\boldsymbol{x}}}_{k-1}\right\|^2+\mathbb{E}\left(\frac{\mu}{2}\left\|{\boldsymbol{y}}_t-{\boldsymbol{x}}_*\right\|^2+\right. \left.\left\langle{\boldsymbol{g}}_t, {\boldsymbol{x}}_*-{\boldsymbol{x}}_{t+1}\right\rangle+\left\langle{\boldsymbol{g}}_t, {\boldsymbol{x}}_{t+1}-{\boldsymbol{x}}_t\right\rangle\right) \\ \geqslant f\left({\boldsymbol{y}}_t\right)+\frac{1-\theta}{\theta}\left(f\left({\boldsymbol{y}}_t\right)-f\left(\tilde{{\boldsymbol{x}}}_{k-1}\right)\right)+\mathbb{E}\left(\chi_{t+1}-\right. \\ \left.\frac{1}{1+\eta \sigma} \chi_t\right)+\mathbb{E}\left(\left\langle{\boldsymbol{g}}_t, {\boldsymbol{x}}_{t+1}-{\boldsymbol{x}}_t\right\rangle+\frac{\alpha L}{2 \eta} \| {\boldsymbol{x}}_t-\right. \\ {\boldsymbol{x}}_{t+1} \|^2 \\ \geqslant f\left({\boldsymbol{y}}_t\right)+\frac{1-\theta}{\theta}\left(f\left({\boldsymbol{y}}_t\right)-f\left(\tilde{{\boldsymbol{x}}}_{k-1}\right)\right)+\mathbb{E}\left(\chi_{t+1}-\right. \\ \left.\frac{1}{1+\eta \sigma} \chi_t\right)+\frac{1}{\theta} \mathbb{E}\left(f\left({\boldsymbol{y}}_{t+1}\right)-f\left({\boldsymbol{y}}_t\right)-\right. \\ \left.\left.\frac{2 \eta \theta}{\alpha-\eta \theta}\left(f\left({\boldsymbol{y}}_t\right)-f^*+f\left(\tilde{{\boldsymbol{x}}}_{k-1}\right)-f^*\right)\right)\right) = \mathbb{E}\left(\chi_{t+1}-\frac{1}{1+\eta \sigma} \chi_t\right)+ \\ \frac{1}{\theta} \mathbb{E}\left(f\left({\boldsymbol{y}}_{t+1}\right)-f^*\right)+\left(1+\frac{1-\theta}{\theta}-\frac{1}{\theta}\right)\left(f\left({\boldsymbol{y}}_t\right)-\right. \\ \left.f^*\right)-\frac{1-\theta}{\theta}\left(f\left(\tilde{{\boldsymbol{x}}}_{k-1}\right)-f^*\right)-\frac{2 \eta}{\alpha-\eta \theta}\left(f\left({\boldsymbol{y}}_t\right)-f^*\right)- \\ \frac{2 \eta}{\alpha-\eta \theta}\left(f\left(\tilde{{\boldsymbol{x}}}_{k-1}\right)-f^*\right)+f^*. \end{array} $ |
其中:第1个不等式利用了f的μ-强凸性, 第2个等式利用算法1中的设定yt=θxt+(1-θ)
由此, 整理可得
| $ \begin{aligned} & \mathbb{E} \chi_{t+1}+\frac{1}{\theta} \mathbb{E}\left(f\left({\boldsymbol{y}}_{t+1}\right)-f^*\right) \\ \leqslant & \frac{1}{1+\eta \sigma} \chi_t+\frac{2 \eta}{\alpha-\eta \theta}\left(f\left({\boldsymbol{y}}_t\right)-f^*\right)+ \\ & \left(\frac{1-\theta}{\theta}+\frac{2 \eta}{\alpha-\eta \theta}\right)\left(f\left(\tilde{{\boldsymbol{x}}}_{k-1}\right)-f^*\right). \end{aligned} $ |
注意到由引理5.4, 为使得
| $ \frac{2 \eta}{\alpha-\eta \theta} \leqslant \frac{1}{1+\eta \sigma} \frac{1}{\theta}, $ | (A) |
只需要
| $ \mathbb{E} \chi_{t+1}+\frac{1}{\theta} \mathbb{E}\left(f\left(\boldsymbol{y}_{t+1}\right)-f^*\right)\\ \leqslant \frac{1}{1+\eta \sigma} \chi_t+\frac{1}{1+\eta \sigma} \frac{1}{\theta}\left(f\left(\boldsymbol{y}_t\right)-f^*\right)+ \\ \left(\frac{1-\theta}{\theta}+\frac{2 \eta}{\alpha-\eta \theta}\right)\left(f\left(\tilde{\boldsymbol{x}}_{k-1}\right)-f^*\right). $ |
对上式取全期望, 定义
| $ \begin{aligned} & \mathfrak{L}_{t+1} \leqslant \frac{1}{1+\eta \sigma} \mathfrak{L}_t+\left(\frac{1-\theta}{\theta}+\right. \\ & \left.\frac{2 \eta}{\alpha-\eta \theta}\right) \frac{L}{2} \mathbb{E}\left\|\tilde{{\boldsymbol{x}}}_{k-1}-{\boldsymbol{x}}_*\right\|^2 . \end{aligned} $ |
反复利用上式, 可得
| $ \begin{gathered} \mathfrak{L}_m \leqslant\left(\frac{1}{1+\eta \sigma}\right)^m\left(\mathbb{E} \chi_0+\frac{1}{\theta} \frac{L}{2} \mathbb{E}\left\|\tilde{{\boldsymbol{x}}}_{k-1}-{\boldsymbol{x}}_*\right\|^2\right)+ \\ \left(\frac{1-\theta}{\theta}+\frac{2 \eta}{\alpha-\eta \theta}\right) \frac{L}{2} \frac{1+\eta \sigma}{\eta \sigma} \mathbb{E}\left\|\tilde{{\boldsymbol{x}}}_{k-1}-{\boldsymbol{x}}_*\right\|^2. \end{gathered} $ |
其中利用了x0 = y0 =
| $ \begin{aligned} & \mathbb{E} \chi_m \leqslant\left(\frac{1}{1+\eta \sigma}\right)^m\left(\mathbb{E} \chi_0+\frac{1}{\theta} \frac{L}{2} \mathbb{E}\left\|\tilde{{\boldsymbol{x}}}_{k-1}-{\boldsymbol{x}}_*\right\|^2\right)+ \\ & \left(\frac{1-\theta}{\theta}+\frac{2 \eta}{\alpha-\eta \theta}\right) \frac{L}{2} \frac{1+\eta \sigma}{\eta \sigma} \mathbb{E}\left\|\tilde{{\boldsymbol{x}}}_{k-1}-{\boldsymbol{x}}_*\right\|^2. \end{aligned} $ |
回忆定义
| $ \begin{gathered} \mathbb{E}\left\|\tilde{{\boldsymbol{x}}}_k-{\boldsymbol{x}}_*\right\|^2 \leqslant\left(\left(\frac{1}{1+\eta \sigma}\right)^m\left(1+\frac{\eta}{\alpha \theta(1+\eta \sigma)}\right)+\right. \\ \left.\frac{1}{\alpha \sigma}\left(\frac{1-\theta}{\theta}+\frac{2 \eta}{\alpha-\eta \theta}\right)\right) \mathbb{E}\left\|\tilde{{\boldsymbol{x}}}_{k-1}-{\boldsymbol{x}}_*\right\|^2,\end{gathered} $ |
其中利用了算法1对快照的选择方式
由β的定义, 上式即
| $ \mathbb{E}\left\|\tilde{{\boldsymbol{x}}}_k-{\boldsymbol{x}}_*\right\|^2 \leqslant \beta \mathbb{E}\left\|\tilde{{\boldsymbol{x}}}_{k-1}-{\boldsymbol{x}}_*\right\|^2. $ | (14) |
注意β定义式里含有η=ηk-1(其中(k-1)是目前被取定和分析的外循环数), 因而此处的β是依赖于k的。下面将分析β定义式里的各个项并推导出β的一个不依赖于k的上界, 从而可以反复利用式(14)形式的递推式而得到收敛性结果。利用引理5.4, 有
| $ \begin{array}{l} \left(\frac{1}{1+\eta \sigma}\right)^m =\left(1-\frac{\eta \sigma}{1+\eta \sigma}\right)^m \leqslant \exp \left(\frac{-\eta \sigma}{1+\eta \sigma} m\right) \\ \leqslant \exp \left(\frac{-\frac{\sigma}{m L}}{1+\frac{\sigma}{m \mu}} m\right) \\=\exp \left(\frac{-\frac{\sigma}{L}}{1+\frac{\sigma}{m \mu}}\right) \xrightarrow{{\text { as }} m \rightarrow \infty} \exp \left(-\frac{\sigma}{L}\right) . \end{array} $ |
由以上的极限式, 记M2为使得
| $ \left(\frac{1}{1+\eta \sigma}\right)^m \leqslant \exp \left(-\frac{\sigma}{L}\right)+\delta. $ | (B) |
成立的最小正整数, 则当m≥M2时, 有
| $ 1+\frac{\eta}{\alpha \theta(1+\eta \sigma)} \leqslant 1+\delta , $ | (C) |
只需要
| $ \frac{1}{\alpha \sigma} \frac{2 \eta}{\alpha-\eta \theta} \leqslant \frac{\delta^2}{3}, $ | (D) |
只需
| $ \frac{1}{\alpha \sigma} \frac{1-\theta}{\theta} \leqslant \frac{\delta^2}{2} . $ |
综上, 定义M
| $ \mathbb{E}\left\|\tilde{{\boldsymbol{x}}}_k-{\boldsymbol{x}}_*\right\|^2 \leqslant\left(1-\frac{\delta^2}{6}\right) \mathbb{E}\left\|\tilde{{\boldsymbol{x}}}_{k-1}-{\boldsymbol{x}}_*\right\|^2. $ | (15) |
此时注意各个Mi的获得基于引理5.4, 而引理5.4给出了对任何可能的BB步长的不依赖于外循环数的上下界。所以对不同的k,为保证式(15)成立而要求的内循环长度下界M的值是同一的, 故式(15)在m≥M的前提下对所有k∈{1, 2, …, l}都成立。反复利用此式, 则定理得证。
6 数值实验本节将SVRG-BB-Katyusha与SVRG-BB-Katyusha-SPARSE应用于求解二分类问题的L2正则逻辑回归模型给出实验结果, 模型的分量函数如下
| $ f_i({\boldsymbol{x}})=\log \left(1+\exp \left(-a_i {\boldsymbol{b}}_i^{\mathrm{T}} {\boldsymbol{x}}\right)\right)+\frac{\lambda}{2}\|{\boldsymbol{x}}\|^2. $ |
其中:ai∈{-1, 1},
① 数据集网址: https://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/
|
|
表 1 数据集信息 Table 1 Dataset information |
图 2~图 4中, x轴代表外循环数, y轴代表优化间隙, 即一定外循环数k对应的快照处目标函数值与目标函数最小值之差
| $ L=\lambda+\frac{L^*}{n} \sum\limits_{i=1}^n\left\|{\boldsymbol{b}}_i\right\|^2, L^*=\frac{\sqrt{3}}{18} . $ |
|
Download:
|
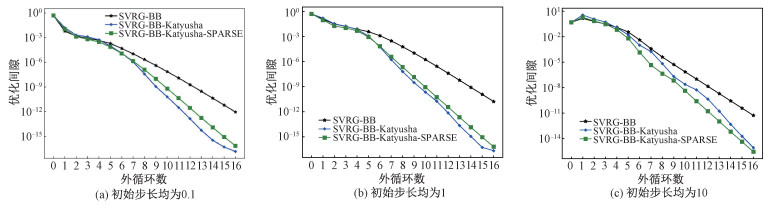
| 图 2 ijcnn1数据集实验结果 Fig. 2 Experimental results of ijcnn1 dataset | |

|
Download:
|
| 图 3 w8a数据集实验结果 Fig. 3 Experimental results of w8a dataset | |
|
Download:
|
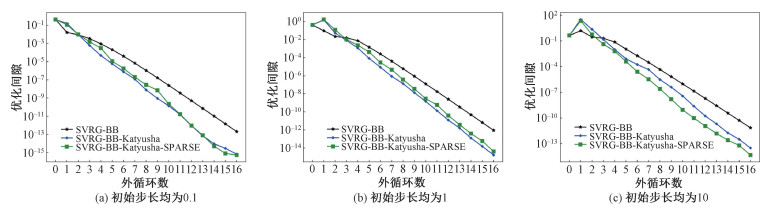
| 图 4 rcv1数据集实验结果 Fig. 4 Experimental results of rcv1 dataset | |
总设定动量控制系数为θ=0.9。对于算法2, 总设定m0=4。考虑到所测试算法的随机性, 对所有算法在相应设定下均运行了10次, 取数值平均后绘制图线。
图 2~图 4分别给出ijcnn1、w8a和rcv1数据集上的实验结果。
根据结果图, 可以得到如下2点观察: 其一, SVRG-BB-Katyusha与SVRG-BB-Katyusha-SPARSE在外循环数相同时, 最后输出点(即最后一个外循环末所得到的新快照)总拥有相较于SVRG-BB更小的优化间隙。具体地, 它们在ijcnn1与rcv1数据集上的表现较好, 优化间隙有若干数量级的领先, 而在w8a数据集上的表现较差, 优化间隙在选取较小或较大的初始步长时只有较微小的领先;其二, 使用m0=4的设定, 算法2所执行的带Katyusha动量的内循环迭代次数约为算法1的25 %,而在表现上仍能保持相近, 甚至在一些情况下具有更优的表现。总之, 所提出的算法1与算法2在实际数值实验中效果优良, 以优化间隙为评价标准时相较于SVRG-BB有较为稳定且可观的优势。
7 结论本文指出SVRG-BB的算法设计带来了“进展-自适应步长有效性”的权衡问题, 且该问题是制约SVRG-BB实际表现的一个因素。据此提出并引入新的Katyusha动量作用形式以处理该权衡问题, 通过在上述权衡中取得更好平衡来获得在优化间隙意义下更好的实际表现, 并给出所得到的SVRG-BB-Katyusha算法的线性收敛性质的证明。基于“贪婪”思想, 进一步提出SVRG-BB-Katyusha-SPARSE算法以减少带Katyusha动量的内循环迭代带来的额外计算量。在公开数据集上的数值实验表明所提出的2个方法相较于SVRG-BB具有较明显的优势, 即在达到一定外循环数时优化间隙有若干个数量级的减小。
| [1] |
Robbins H, Monro S. A stochastic approximation method[J]. The Annals of Mathematical Statistics, 1951, 22(3): 400-407. Doi:10.1214/aoms/1177729586 |
| [2] |
Bottou L. Stochastic gradient learning in neural networks[EB/OL]. (2006-04-20)[2023-12-26]. http://leon.bottou.org/papers/bottou-91c.
|
| [3] |
Nemirovski A, Juditsky A, Lan G, et al. Robust stochastic approximation approach to stochastic programming[J]. SIAM Journal on Optimization, 2009, 19(4): 1574-1609. Doi:10.1137/070704277 |
| [4] |
Zhang T. Solving large scale linear prediction problems using stochastic gradient descent algorithms[C]//Proceedings of the 21st International Conference on Machine Learning. July 4-8, 2004, Banff, Alberta, Canada. ACM, 2004. DOI: 10.1145/1015330.1015332.
|
| [5] |
赵文深, 韩丛英, 金玲子. 求解带大量凸约束的随机优化问题的随机增广拉格朗日算法[J/OL]. (2023-06-21)[2023-12-26]. 中国科学院大学学报. DOI: 10.7523/j.ucas.2023.055.
|
| [6] |
Bottou L, Curtis F E, Nocedal J. Optimization methods for large-scale machine learning[J]. SIAM Review, 2018, 60(2): 223-311. Doi:10.1137/16M1080173 |
| [7] |
Le Roux N, Schmidt M, Bach F. A stochastic gradient method with an exponential convergence rate for finite training sets[EB/OL]. (2012-02-28)[2023-12-26]. https://doi.org/10.48550/arXiv.1202.6258.
|
| [8] |
Schmidt M, Le Roux N, Bach F. Minimizing finite sums with the stochastic average gradient[J]. Mathematical Programming, 2017, 162(1): 83-112. Doi:10.1007/s10107-016-1030-6 |
| [9] |
Defazio A, Bach F, Lacoste-Julien S. SAGA: a fast incremental gradient method with support for non-strongly convex composite objectives[C]. Proceedings of the 27th International Conference on Neural Information Processing Systems-Volume 1. December 8-13, 2014, Montreal, Canada. ACM, 2014: 1646-1654. DOI: 10.5555/2968826.2969010.
|
| [10] |
Raj A, Stich S U. k-SVRG: variance reduction for large scale optimization[EB/OL]. 2018: arXiv: 1805.00982. (2018-05-02)[2023-12-26]. https://arxiv.org/abs/1805.00982.
|
| [11] |
Driggs D, Liang J W, Schönlieb C B. On biased stochastic gradient estimation[EB/OL]. 2019: arXiv: 1906.01133. (2019-06-04)[2023-12-26]. http://arxiv.org/abs/1906.01133.
|
| [12] |
Johnson R, Zhang T. Accelerating stochastic gradient descent using predictive variance reduction[J]. Advances in Neural Information Processing Systems, 2013, 26. Doi:10.5555/2999611.2999647 |
| [13] |
Konečný J, Richtárik P. Semi-stochastic gradient descent methods[J]. Frontiers in Applied Mathematics and Statistics, 2017, 3: 9. Doi:10.3389/fams.2017.00009 |
| [14] |
Kovalev D, Horváth S, Richtárik P. Don't jump through hoops and remove those loops: SVRG and Katyusha are better without the outer loop[EB/OL]. 2019: arXiv: 1901.08689. (2019-06-05)[2023-12-26] http://arxiv.org/abs/1901.08689.
|
| [15] |
Lei L H, Jordan M I. On the adaptivity of stochastic gradient-based optimization[J]. SIAM Journal on Optimization, 2020, 30(2): 1473-1500. Doi:10.1137/19M1256919 |
| [16] |
Shang F H, Zhou K W, Liu H Y, et al. VR-SGD: a simple stochastic variance reduction method for machine learning[J]. IEEE Transactions on Knowledge and Data Engineering, 2020, 32(1): 188-202. Doi:10.1109/TKDE.2018.2878765 |
| [17] |
Nguyen L M, Liu J, Scheinberg K, et al. SARAH: a novel method for machine learning problems using stochastic recursive gradient[C]//Proceedings of the 34th International Conference on Machine Learning-Volume 70. August 6-11, 2017, Sydney, NSW, Australia. ACM, 2017: 2613-2621. DOI: 10.5555/3305890.3305951.
|
| [18] |
Xiao L, Zhang T. A proximal stochastic gradient method with progressive variance reduction[J]. SIAM Journal on Optimization, 2014, 24(4): 2057-2075. Doi:10.1137/140961791 |
| [19] |
Morin M, Giselsson P. Sampling and update frequencies in proximal variance-reduced stochastic gradient methods[EB/OL]. 2020: arXiv: 2002.05545. (2020-02-13)[2023-12-26]. https://arxiv.org/abs/2002.05545.
|
| [20] |
Ying B C, Yuan K, Sayed A H. Variance-reduced stochastic learning under random reshuffling[J]. IEEE Transactions on Signal Processing, 2020, 68: 1390-1408. Doi:10.1109/TSP.2020.2968280 |
| [21] |
Allen-Zhu Z. Katyusha: The first direct acceleration of stochastic gradient methods[C]//Proceedings of the 49th Annual ACM SIGACT Symposium on Theory of Computing. June 19-23, 2017, Montreal, Canada. ACM, 2017: 1200-1205. DOI: 10.1145/3055399.3055448.
|
| [22] |
Zhou K W, Shang F H, Cheng J. A simple stochastic variance reduced algorithm with fast convergence rates[EB/OL]. 2018: arXiv: 1806.11027. (2018-06-28)[2023-12-26]. http://arxiv.org/abs/1806.11027.
|
| [23] |
Lan G H, Zhou Y. An optimal randomized incremental gradient method[J]. Mathematical Programming, 2018, 171(1): 167-215. Doi:10.1007/s10107-017-1173-0 |
| [24] |
Tan C H, Ma S Q, Dai Y H, et al. Barzilai-Borwein step size for stochastic gradient descent[C]//Proceedings of the 30th International Conference on Neural Information Processing Systems. December 5-10, 2016, Barcelona, Spain. ACM, 2016: 685-693. DOI: 10.5555/3157096.3157173.
|
| [25] |
Dubois-Taine B, Vaswani S, Babanezhad R, et al. SVRG meets AdaGrad: painless variance reduction[J]. Machine Learning, 2022, 111(12): 4359-4409. Doi:10.1007/s10994-022-06265-x |
| [26] |
Shi Z, Sadiev A, Loizou N, et al. AI-SARAH: adaptive and implicit stochastic recursive gradient methods[EB/OL]. 2021: arXiv: 2102.09700. (2021-02-19)[2023-12-26]. https://arxiv.org/abs/2102.09700.
|
| [27] |
Liu Y, Han C, Guo T. A class of stochastic variance reduced methods with an adaptive stepsize[EB/OL]. (2019-04-07)[2023-12-26]. http://www.optimization-online.org/DB_FILE/2019/04/7170.
|
| [28] |
Barzilai J, Borwein J M. Two-point step size gradient methods[J]. IMA Journal of Numerical Analysis, 1988, 8(1): 141-148. Doi:10.1093/imanum/8.1.141 |
| [29] |
Yang Z, Chen Z F, Wang C. Accelerating mini-batch SARAH by step size rules[J]. Information Sciences, 2021, 558: 157-173. Doi:10.1016/j.ins.2020.12.075 |
| [30] |
Yu T T, Liu X W, Dai Y H, et al. A minibatch proximal stochastic recursive gradient algorithm using a trust-region-like scheme and Barzilai-Borwein stepsize[J]. IEEE Transactions on Neural Networks and Learning Systems, 2021, 32(10): 4627-4638. Doi:10.1109/TNNLS.2020.3025383 |
| [31] |
Yu T T, Liu X W, Dai Y H, et al. A mini-batch proximal stochastic recursive gradient algorithm with diagonal Barzilai-Borwein stepsize[J]. Journal of the Operations Research Society of China, 2023, 11(2): 277-307. Doi:10.1007/s40305-022-00436-2 |
| [32] |
Xie B H, Jin C H, Zhou K W, et al. An adaptive incremental gradient method with support for non-Euclidean norms[EB/OL]. 2022: arXiv: 2205.02273. (2022-06-28)[2023-12-26]. http://arxiv.org/abs/2205.02273.
|
| [33] |
Kingma D P, Ba J. Adam: a method for stochastic optimization[EB/OL]. 2014: arXiv: 1412.6980. (2014-12-22)[2023-12-26]. https://arxiv.org/abs/1412.6980.
|
 2024, Vol. 41
2024, Vol. 41 


