三维点云已在基础测绘、无人驾驶、数字孪生等领域得到广泛应用，然而实际应用中的点云数据多达数亿甚至TB级，不仅占用大量的存储空间，对数据处理、管理、共享与应用带来极大挑战，也对点云压缩提出更高的要求^[1]。

精确的点云几何信息对三维场景的表示效果至关重要，几何信息压缩通常基于树结构编码实现。Schnabel和Klein^[2]基于八叉树划分点云，并基于局部表面估计预测渐进式压缩八叉树。Kammerl等^[3]提出帧间的点云压缩算法，采用异或方式编码八叉树节点间的差异，以消除帧内、帧间的冗余点云，然后通过算术编码压缩，将点细节编码为点云与体素的相对关系，该算法已被集成至PCL(point cloud library)。律帅等^[4]提出基于数据类型转换的点云有损压缩，将浮点数类型点云转为整数类型，提高了压缩率。近年来深度学习在点云压缩方面取得了一定的进展，主要有基于点、基于八叉树和基于体素3种框架^[5]。Yan等^[6]基于PointNet框架思想，结合最远点采样与深度自编码器，将编码后的特征作为压缩结果，但解压缩的点数固定，且与原始点云误差较大。Huang等^[7]构建点云八叉树来训练能够结合上下文信息估计八叉树节点条件概率分布的多层感知机(multilayer perceptron, MLP)，并用熵编码实现高压缩率低失真的点云压缩。Biswas等^[8]在此基础上提出一个时空熵模型多帧点云的八叉树节点，实现了帧间点云压缩，进一步提高压缩性能。Quach等^[9]首次提出基于体素的深度学习点云压缩算法，采用三维卷积神经网络(3D convolutional neural network, 3D CNN)构建自编码器，提取隐变量并运用Deflate算法进行压缩。Guarda等^[10]基于3D CNN进一步提取隐变量和超先验特征，并将其作为概率模型参数辅助熵编码压缩。徐嘉诚等^[11]提出基于深度卷积生成对抗网络(deep convolution generative adversarial networks，DCGAN) 的端到端点云有损压缩模型，重构生成器和判别器实现了较高视觉质量的点云有损压缩。Wang等^[12]利用三维空洞卷积实现渐进尺度升降，在每一个尺度编码重构点云，但未能充分利用尺度间的关系。此外，还可以将点云转为图像，利用深度学习压缩图像^[13]，如利用距离、航偏角和波束ID构建图像表征点云数据，采用带有残差块的循环神经网络搭建自编码器，实现端到端的点云压缩，但仅支持车载激光点云。

综上，当前的深度学习点云压缩算法依然存在失真率较高、尺度信息利用不充分等问题。本文提出一种基于深度变分自编码的多尺度注意力点云几何信息压缩算法(multi-scale attention point cloud geometry compression, MSA-GPCC)，利用基于体素的深度自编码器提取点云的多尺度特征，并引入多尺度模块和注意力机制实现多尺度特征融合，进而建立更准确的深度熵模型，结合熵编码以实现点云高码率、低失真的高效压缩。

1 研究方法

MSA-GPCC针对八叉树分块后体素化的点云进行压缩，通过基于多尺度特征和注意力机制的深度变分自编码器训练得到深度熵模型，熵编码和熵解码在深度熵模型的约束下实现点云几何信息的压缩和解压缩，技术路线如图 1所示。

1.1 点云八叉树划分及体素表示

首先基于八叉树将点云划分为多个块，以平衡压缩效果与显存压力。将每一个块单独输入模型进行压缩，从而支持大规模并行压缩。对每一个分块点云，划分分辨率为r的体素格网，将格网内存在点云的体素赋值为1，否则赋为0，从而支持基于3D卷积的空间关系提取。

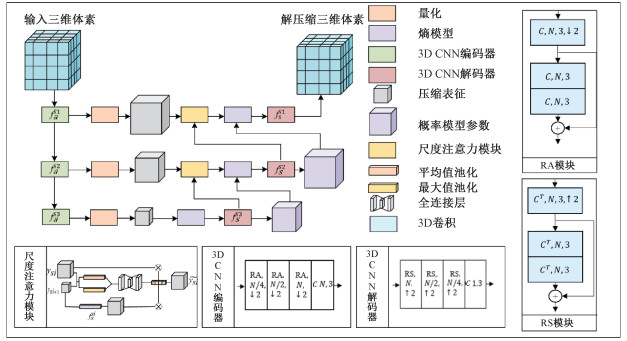
1.2 基于多尺度特征和注意力机制的深度变分自编码框架

MSA-GPCC基于变分自编码器框架，编码器f_a与解码器f_s采用3D CNN结构，通过3个不同尺度的3D CNN模块提取点云体素v_S的多尺度特征y_si，再通过尺度注意力融合多尺度特征建立熵模型，并进行量化得到$ \tilde{y} $。最后，基于3D CNN解码器估算熵模型$ \hat{p}(y) $的概率模型参数，实现高效熵编码，模型结构如图 2所示。

3D CNN编解码器由多个编码残差块RA与解码残差块RS堆叠而成，其中N代表卷积核个数，↓2代表空洞卷积的空洞率，卷积核大小均为3×3×3。

模型中的尺度注意力模块能够更好地融合不同尺度信息，通过平均值池化和最大值池化分别对特征的空间和通道维聚合，将聚合特征映射的空间信息输入至一个共享权重的全连接层中，得到尺度注意力权重值，最后基于该权重融合2个不同尺度的特征。

1.3 多尺度深度熵模型

对于压缩表征y的信源概率$ \hat{p}(y) $，采用不同尺度y_si的联合分建模，如下式

$ \begin{aligned} & \hat{p}(y)=p\left(y_{s 1}, \cdots, y_{s 3}\right)= \\ & \prod\limits_{s i \in(1, 3)} p\left(y_{s i} \mid y_{s i+1}, \cdots, y_{s 3}\right). \end{aligned} $

(1)

其中：y_si为尺度si的特征图。采用均值为0的高斯模型^[9] $ \varkappa\left(0, \sigma^2\right) $建模y_s1与y_s2，假设y_s3服从均匀分布^[14]，则y_si条件概率分布表示为

$ \begin{gathered} p\left(y_{s i} \mid y_{s i+1}, \cdots, y_{s 3}\right)=p\left(y_{s i} \mid f_a^{s i+1}\right)= \\ \left(N\left(0, \sigma^{s i 2}\right) \times U\left(-\frac{1}{2}, \frac{1}{2}\right)\right)\left(y_i\right). \end{gathered} $

(2)

其中：f_a^si+1为尺度si+1的编码器，用于估计$ \varkappa\left(0, \sigma^2\right) $的参数σ。选择3层编码器f_a^si和解码器f_s^si取多尺度的隐变量y_si，如下式。首先输入体素v_S到第1层编码器f_a^s1得到隐变量y_s1，再通过第2层f_a^s2得到下一尺度的y_s2，y_s2输入第3层f_a^s3得到第3尺度的y_s3。每一尺度的$ \tilde{y}_{s i}$均由y_si经过量化器Q得到，再与下一尺度解码器f_s^s-1解码的特征图通过尺度注意力模块融合，输入当前尺度解码器f_hs中，得到$ \varkappa\left(0, \sigma^2\right) $的参数$ \tilde{\sigma} $。基于$ \varkappa\left(0, \tilde{\sigma}^2\right) $建模隐变量$ \tilde{y_{s i}}$，最后通过解码器f_s得到解压缩后的体素$ \tilde{v_S} $。

$ \begin{gathered} y_{s 1}=f_a^{s 1}\left(v_S\right), \tilde{y_{s 1}}=Q\left(y_{s 1}\right), \\ \tilde{v_S}=f_s^{s 1}\left(\tilde{y_{s 1}}, f_s^{s 2}\right), y_{s 2}=f_a^{s 2}\left(y_{s 1}\right), \\ \tilde{y_{s 2}}=Q\left(y_{s 2}\right), \tilde{\sigma}^{s 1}=f_s^{s 2}\left(\tilde{y_{s 2}}, f_s^{s 3}\right), \\ y_{s 3}=f_a^{s 3}\left(y_{s 2}\right), \tilde{y_{s 3}}=Q\left(y_{s 1}\right), \\ \tilde{\sigma}^{s 2}=f_s^{s 3}\left(\tilde{y_{s 3}}\right). \end{gathered} $

(3)

1.4 损失函数

MSA-GPCC的目标函数L可以在最小化压缩率R的同时降低失真率D，通过引入权重因子λ，如下式

$ L=R+\lambda D . $

(4)

压缩率R的优化等价于最小化$ \tilde{y_{s i}} $概率分布的连续熵，如下式

$ \begin{gathered} R=\left(-\log _2 p\left(y_{s 1} \mid y_{s 2}, y_{s 3}\right)\right)+ \\ \left(-\log _2 p\left(y_{s 2} \mid y_{s 3}\right)\right)+\left(-\log _2 p\left(y_{s 3}\right)\right). \end{gathered} $

(5)

由于激光扫描仪获取的点云数据往往在空间分布不均匀，体素化后80 % 以上的体素为空体素，因此空体素与非空体素之间存在极大的类别不平衡，导致在失真率D的优化过程中使模型收敛于空体素。Focal loss在交叉熵损失函数的基础上增加类别权重α和类别难度因子γ以缓解类别不平衡问题，如下式

$ D={\rm{FL}}\left(p_t\right)=-\alpha_t\left(1-p_t\right)^\gamma \log \left(p_t\right) . $

(6)

2 实验结果与分析 2.1 实验数据

模型训练基于ModelNet40^[15]数据集，模型评估8iVSLF^[16]静态点云数据集中的4个点云数据：longdress、loot、redandblack和soldier，以及Microsoft Voxelized Upper Bodies^[17]点云数据集中的数据ricardo9，如图 3所示。

选择MPEG的TMC13 G-PCC基线算法^[18]，以及基于深度学习的点云压缩算法(deep learing-based point cloud compression，D-PCC)^[9]。

2.2 评价指标

压缩率通过单点所占位数(bits per point, bpp)衡量，失真率基于点间(D₁)和点与平面(D₂)误差的峰值信噪比(peak signal to noise ratio, PSNR)评价，如下

$ \mathrm{PSNR}=10 \times \lg \left(\frac{\mathrm{MAX}_A^2}{D}\right). $

(7)

其中：MAX_A代表点云A的信号峰值，即位深精度。D₁误差为A点云中点a_i与B点云中最邻近点b_j的平均误差^[16]，D₂误差为误差向量延法线n_i方向的投影^[19]。

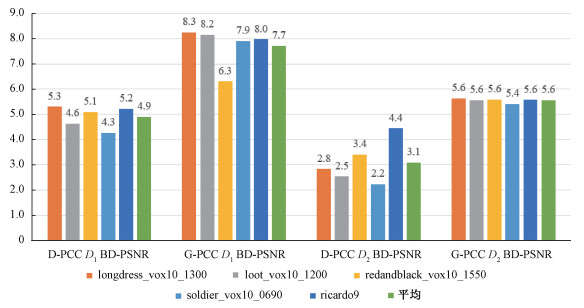
2.3 结果与分析

为充分评价MSA-GPCC在不同压缩率与失真率权重下的性能，分别训练λ取1×10^-5~2×10^-4的不同模型，计算MSA-GPCC与G-PCC、D-PCC的D₁、D₂的BD-PSNR(图 4)。MSA-GPCC在5个数据集上的性能均优于基线算法：本文算法对比D-PCC的平均D₁ BD-PSNR为4.91 dB，D₂ BD-PSNR为3.09 dB。5个数据集中，longdress数据上的D₁ BD-PSNR最高，为+5.30 dB，ricardo9数据集的D₂ BD-PSNR最高，为+4.45 dB；对比G-PCC，MSA-GPCC的平均D₁ BD-PSNR为7.72 dB，D₂ BD-PSNR为5.56 dB。

进一步比较算法解压缩的视觉效果，选择λ=2×10^-5时的MSA-GPCC与D-PCC模型压缩并解压缩loot数据集，逐点计算解压缩前后的D₁误差，图 5中颜色越亮代表该位置解压缩后误差越大。G-PCC的失真最严重，且分布均匀，D-PCC失真率相对较低，大多集中在分块边界区域，MSA-GPCC的失真率最小，且bpp仅为0.70，优于D-PCC的0.90和G-PCC的0.71。

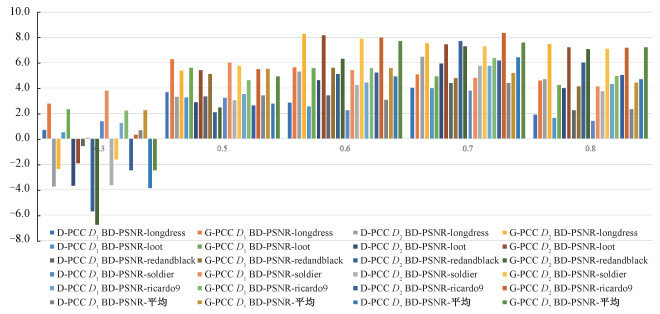
为分析MSA-GPCC的压缩性能对focal loss中类别权重α的敏感性，设计α为0.3、0.5、0.6、0.7、0.8的5组实验，结果如图 6和图 7所示。α=0.3时，模型的D₁和D₂指标均最差，在5个数据集上平均D₁ BD-PSNR相比G-PCC降低3.86 dB、相比D-PCC提高0.66 dB，D₂ BD-PSNR相比G-PCC提高2.24 dB、相比D-PCC降低2.48 dB。相比于G-PCC，α=0.6时的平均D₁ BD-PSNR和D₂ BD-PSNR最优(+5.56 dB，+7.72 dB)。相比于D-PCC，α=0.7时模型的平均D₁和D₂性能均最优(+4.40 dB，+6.41 dB)。

最后分析不同λ时模型解压缩的D₁精度，如表 1与图 8所示。λ越低，模型压缩率越高，但失真率也越大，误差集中分布于分块边界区域，因此应该考虑不同场景所需的失真率(rate-distortion，RD)性能，选择合适的λ以实现失真率与压缩率的权衡。

3 结论

本文提出一种基于多尺度特征和注意力机制的深度变分自编码点云几何信息压缩算法MSA-GPCC。通过设计多尺度深度熵模型压缩点云特征、引入多尺度注意力模块和熵编码等，既解决了类别不平衡的难题，又提升了点云高码率、低失真的压缩性能。最后用实验验证了方法的应用效果。与G-PCC和D-PCC算法相比，本文方法在压缩率和失真率上具有明显优势。本文设计的尺度注意力模块，结合平均值池化和最大值池化，且强化特征向量中每一个值和响应最大值的反馈，从而有效融合了多尺度特征，大大提高了点云有损压缩的RD性能。文中所用的实验场景相对独立，而基于体素的点云压缩算法依赖于基于八叉树的点云分块，因此在应用于连续的大场景时需要考虑八叉树节点间的相关性，同时考虑动态点云压缩，以实现大场景、动态点云的低失真、高码率压缩。