随着城市化进程的加速和人口集聚程度的增加，交通拥堵问题日益严重。交通信号控制(traffic signal control, TSC)作为城市交通管理的关键环节，能够有效提升城市交通系统效率，对于缓解交通拥堵、提高道路通行能力和减少能源消耗有着至关重要的作用。

传统TSC方法以悉尼交通自适应协调控制系统(Sydney coordinated adaptive traffic system, SCATS)^[1]和分周期偏移优化技术(split cycle offset optimizing technique, SCOOT)^[2]为代表。传统TSC方法通过部署传感器或者摄像头获取交通流量数据以检测车辆通过交叉路口的情况，无法及时响应实时的交通状况，容易导致信号灯控制滞后于交通流量的变化^[3-4]。另一方面，传统TSC方法大多依赖于人工预设规则^[5]以及特定交通模型假设^[6]，无法广泛应用于复杂的真实交通道路网络。综上所述，传统TSC方法已经难以适应日益密集的交通流量和瞬息万变的交通环境，能够实时控制调整交通信号灯配时方案的智能控制方法对于TSC系统性能的提升具有重要的现实意义。

不同于传统TSC方法，基于深度强化学习的TSC方法^[7]，如IntelliLight^[8]、CoLight^[9]、Press-Light^[10]以及MetaLight^[11]等，在获取适应复杂交通动态的数据驱动控制模型和自适应学习优化TSC策略上显示出了巨大的潜力，可以更及时、更有效地适应和协调交通^[12]。大量研究成果^[13-17]表明基于深度强化学习的方法在提升道路网络性能方面优于传统TSC方法。然而在大规模城市多交叉路口的场景下，随着状态空间与动作空间维度的增加，传统的单智能体强化学习方法的计算复杂性随之急剧增加^[18]。近年来，也有部分工作研究基于多智能体强化学习^[19-20]的TSC方法。其中，可有效应对多智能体非平稳环境^[21]的基于集中式训练分布式执行框架(centralized training decentralized execution, CTDE)的多智能体强化学习算法正引起广泛关注^[22-24]。在集中式训练阶段，CTDE框架可共享全局范围的数据，从而实现控制策略的协调与优化^[23]。在分布式执行阶段，各交叉口或路段的信号控制智能体，根据本地观测数据以及经过训练的策略，实时地对信号灯进行控制^[24]。然而，当前基于多智能体强化学习算法的TSC方法^[25]大多没有考虑多交叉路口之间的时空依赖性^[26]，而在交通路网中，交叉路口之间的车流量相互影响，其时空依赖特性与整体交流性能息息相关^[27]。因此，设计考虑多交叉路口之间时空依赖特性以及基于CTDE框架的多智能体强化学习算法，对于缓解城市交通拥堵问题有着至关重要的作用。

基于上述考虑，本文将交叉路口作为智能体，提出基于时空依赖关系多智能体强化学习的多路口TSC方法STLight。本文的主要创新点如下：

1) 将多路口TSC问题转化为马尔可夫博弈问题，并定义了相应的观测空间、动作空间和奖励函数。

2) 提出一种基于注意力机制^[20]的时空依赖模块STDM。STDM可分别在时间和空间维度上提取各交叉路口的相关性，并将原始观测数据转化为具有时空特征的状态表示，以有效捕获各交叉路口间的时空依赖性。

3) 基于所提取的时空特征，STLight使用基于CTDE架构的多智能体强化学习算法，能够有效缓解多智能体动态环境的非平稳问题，并进一步提升各智能体之间的协作能力，从而实现对多交叉路口交通信号的协同控制管理。

4) 通过大量仿真实验，验证了本文所提出的STLight方法在不同度量指标上均优于现有的工作。

1 相关工作 1.1 传统TSC方法

1966年，英国运输与道路研究实验所(Transport and Road Research Laboratory, TRRL)^[6]首次提出基于离线配时的TRANSYT计时控制方法。之后TRRL^[2]又在此基础上，开发出以绿信比、周期及相位差优化技术SCOOT为基础的自适应车流控制系统。20世纪70年代，由新南威尔士州公路交通管理局^[1]研发的悉尼交通自适应协调控制系统SCATS，时至今日仍广泛应用于澳大利亚、新西兰以及其他国家的城市。上述传统TSC控制系统虽然能够减少交通拥堵和提高道路使用效率，但它们也存在着无法预测未来交通需求、兼容性差以及易受环境变化影响等缺点。

2008年，Koonce和Rodegerdts^[5]提出预定时控制策略Fixed-Time。2013年，Varaiya^[3]提出基于交通网络中车辆排队压力的自适应交通信号控制策略MaxPressure。同年Cools等^[4]开发出自组织交通信号灯(self organizing traffic lights, SOTL)控制方法。在某些特定场景中，上述算法能够让交通信号灯自适应地响应实际交通需求，从而提高整个交通网络的通行效率。然而上述算法都存在一定的局限性，例如无法处理大规模交通网络中的全局优化问题。

1.2 基于深度强化学习的TSC方法

2016年，Li等^[28]最先尝试将深度Q网络(deep Q-network, DQN)应用于单个交叉路口的交通信号控制；Genders和Razavi^[29]探讨了基于策略梯度(policy gradient, PG)的交通信号控制方法并将其与深度学习技术结合；Aslani等^[30]主要研究在实际交通网络中如何利用基于演员-评论家(actor-critic，AC)方法的自适应交通信号控制来应对不同的交通中断事件，并设计了演员-评论家自适应交通信号(actor-critic adaptive traffic signal, A-CATs)控制方法。2020年，Yang等^[16]提出改进近端策略优化(modified proximal policy optimization, MPPO)算法，从全局角度对交通信号灯和车辆进行控制。2021年，Ge等^[13]提出一种基于多视角编码器实柔性演员-评论家(multi-agent transfer soft actor-critic with the multi-view encoder, MT-SAC)方法。2023年，Huang和Qu^[17]利用近端策略优化(proximal policy optimization, PPO)算法对神经网络进行训练并调整信号相位来获得最优的信号控制策略。同年，Chen等^[31]提出一种基于长短时记忆(long short-term memory, LSTM)网络以及QMIX算法^[32]的多路口TSC方法。同年，Timur等^[14]将异步优势演员-评论家(asynchronous advantage actor-critic, A3C)算法应用于多路口交通信号控制场景中。然而，上述算法大多只考虑单个交叉路口的交通流量状况，缺乏对整个交通网络的协同控制。

2020年，Wang等^[33]提出通过使用时空多智能体强化学习(spatiotemporal multi-agent reinforce-ment learning, STMARL)来协调交通信号控制，以解决交通拥堵问题。2021年，Wu等^[34]提出动态时空图注意力网络(dynamic spatiotemporal graph attention network, DynSTGAT)，通过动态注意力机制捕捉交通流量和模式的时空变化以实现智能自适应信号控制。2022年，Zhao等^[35]探索了基于Transformer的方法在网络化交通信号控制中实现智能合作学习，并通过自注意机制和序列建模提高交通信号控制的智能化水平。然而上述基于多智能体强化学习的方法均没有采用CTDE框架，从而可能导致协调困难、信息不对称、训练不稳定等问题。2023年，Bokade等^[23]提出基于CTDE的大规模交通信号控制多智能体强化学习框架，使得各智能体能够更好地交换信息，从而有助于实现高效的交通信号控制系统。同年，Yan等^[24]提出基于CTDE的交通信号控制方法，使智能体能够根据动态交通流信息实时调整注意力，在更大范围内快速有效地感知交通环境。然而，上述工作都没有考虑交通道路网络的时空特征融合，无法有效捕捉各交叉路口之间的时空相关性，从而极大影响了各交叉路口之间的协同控制能力。

因此，我们提出基于时空依赖模块和集中训练分散执行架构多智能体强化学习的多路口TSC方法STLight，以期有效提升交通信号系统的协同控制能力。

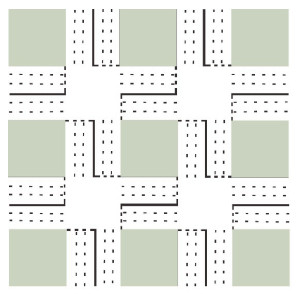
2 系统模型

本文研究交通道路网络中的多交叉路口TSC问题，将由多个交叉路口和连接交叉路口的所有道路组成的交通道路网络建模为简单图$\mathcal{G}=(\mathcal{N}, \varepsilon)$，其中$\mathcal{N}$是交叉路口的集合，ε是道路的集合。交通道路网络由多个交叉路口$n_i \in \mathcal{N}$组成，一条道路e_ij∈ε封闭连接2个相邻的交叉路口n_i和n_j。与当前交叉路口n_i通过道路e_ij直接相连的交叉路口n_j称之为n_i的邻居交叉路口，n_i的邻居交叉路口集合用$\mathcal{N}_i$表示。一个标准的2×2多交叉路口交通道路网络如图 1所示。

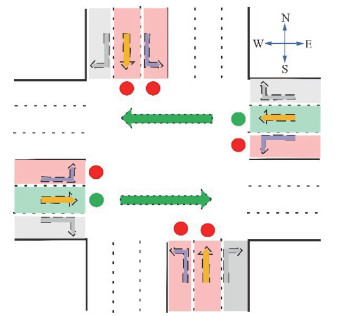
每个交叉路口n_i有4个不同的行驶方向包括东、南、西和北，每个方向的道路由左转、直行和右转共3条车道组成，如图 2所示。接下来，给出部分本文要用到的TSC领域相关概念如下：

1) 交通流量：指在一定时间内通过某道路交通设施的车辆数量。

2) 进口车道和出口车道：进口车道表示车辆即将要进入交叉路口的车道，最右边的车道只允许右转，中间的车道只允许直行，最左边的车道只允许左转，当没有冲突车辆时车辆总是可以右转。出口车道表示车辆即将离开交叉路口的车道。如图 2所示，进口车道和出口车道总数均为12。

3) 交通运动：指车辆通过交叉路口从某进口车道到出口车道。如图 2所示，绿色直箭头表示对应车道允许的交通运动。

4) 交通信号：交通信号决定当前时间是否允许某车道上的车辆移动。如图 2所示，红色信号表示禁止交通运动; 绿色信号表示允许交通运动；黄色信号表示缓冲时段。

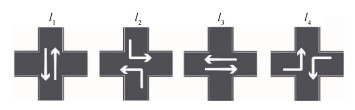
5) 相位：指绿色信号所对应某车道的交通运动，指示当前车辆在当前交叉路口可以行驶的方向，当前相位之外的所有交通运动均被禁止。如图 3所示，本文的默认场景为4向交叉路口，在交通信号控制场景中总共有4个常用相位l₁, l₂, l₃, l₄^[36]，各相位不能处于同一时段。其中l₁代表南北方向直行，l₂代表南北方向左转，l₃代表东西方向直行，l₄代表东西方向左转，右转车道上的车辆随时可右转。

6) 周期：交通信号灯从开始到结束的完整循环时间P。周期包括所有相位的持续时间和相位之间的转换时间，例如红色信号到绿色信号的切换。

7) 绿信比：指一个相位的绿灯时间占整个周期时间的比例。绿信比决定了交叉口各个车道的通行能力。

8) 排队长度：指处于排队状态的车辆数目。如果一辆车在交叉路口行驶速度小于0.1 m/s，则该车被判定为排队状态。

9) 最大绿灯时间和最小绿灯时间：分别指为某一相位分配的最长绿灯时间g_max和最短绿灯时间g_min。

3 问题定义

本文将多路口交通信号协同控制问题定义为多智能体强化学习任务，每个交叉路口都由一个智能体控制。马尔可夫博弈是一种在有限时间内进行的策略决策过程，每个参与者都会根据自己的目标和其他参与者的策略来选择行动。在多智能体强化学习中，每个智能体都试图通过学习来优化自己的策略，以获得最大的回报。智能体的策略选择取决于其当前的状态以及其他智能体的行动和状态。智能体之间的相互作用和竞争使得整个系统具有马尔可夫博弈的特性^[37]。因此本文将该多智能体强化学习任务转化为由元组$\langle\mathcal{N}, \mathcal{O}, \mathcal{S}, \mathcal{A}, \mathcal{P}, r, \gamma, \mu\rangle$定义的马尔可夫博弈(Markov game，MG)问题：

●智能体集合$\mathcal{N}: \mathcal{N}=\left\{n_1, n_2, \cdots, n_{|\mathcal{N}|}\right\}$}是智能体的有限集合。每个智能体n_i控制一个交叉路口，其中i是智能体的索引，1≤i≤ $|\mathcal{N}|$。

●观测$\mathcal{O}: \boldsymbol{o}=\left\{o_1, o_2, \cdots, o_{|\mathcal{N}|}\right\}$是所有智能体的原始观测空间。每个智能体n_i在时刻t从环境中部分观察到的观测值记为o_{i, t}，1≤i≤$|\mathcal{N}|$。

●状态$\mathcal{S}: \boldsymbol{s}=\left\{s_1, s_2, \cdots, s_{|\mathcal{N}|}\right\}$是所有智能体的联合状态空间。每个智能体n_i在时刻t的状态记为s_{i, t}，1≤i≤$|\mathcal{N}|$。

●动作$\mathcal{A}: \boldsymbol{a}=\left\{a_1, a_2, \cdots, a_{|\mathcal{N}|}\right\}$是所有智能体的联合动作空间。每个智能体n_i可以在时刻t决定动作a_{i, t}，1≤i≤$|\mathcal{N}|$。

●转移函数$\mathcal{P}$：转移函数$\mathcal{P}\left(\boldsymbol{s}_{t+1} \mid \boldsymbol{s}_t, \boldsymbol{a}_t\right)$将时刻t的状态-动作对映射到时刻t+1的状态。

●奖励函数r：r_t是所有智能体在时刻t的累计总奖励，定义如下

$ r_t=\sum\limits_{i=1}^{|\mathcal{N}|} \sum\limits_{k=0}^{\infty} \gamma^k r_{i, t+k}, $

(1)

其中每个智能体n_i在时刻t采取动作a_{i, t}后的即时奖励记为r_{i, t}，1≤i≤$|\mathcal{N}|$。

●折现因子γ：γ∈[0, 1]为折现因子，它可以平衡即时奖励和未来奖励。

●策略μ：μ_i表示智能体n_i基于其对环境的观察而采取的行为方式。

马尔可夫博弈的目标是寻找最优的联合策略μ={μ₁, μ₂, …, μ_{$|\mathcal{N}|$}}，使得系统能够最大化总累积奖励r_t。智能体n_i的Q函数定义为Q_i^μ(o, a)。在不引起歧义的情况下，在后续章节中省略部分变量的时间下标t。

4 多路口TSC方法STLight

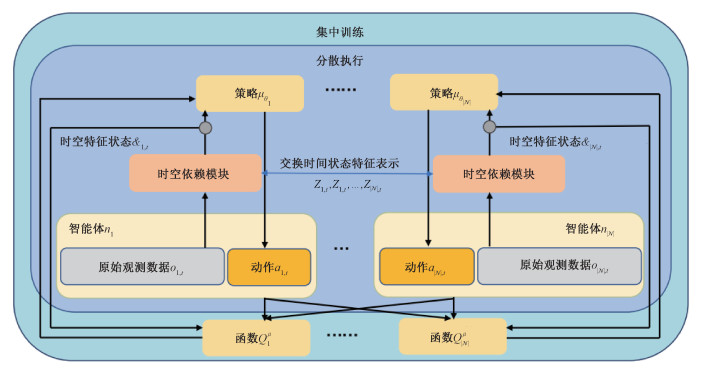
本文提出的STLight方法主要由时空依赖模块STDM和基于集中训练分散执行框架的多智能体强化学习两部分组成。STLight假定每个智能体n_i控制一个交叉路口的交通信号，智能体之间可交换信息。如图 4所示，STLight的基本工作流程如下：1)在时空依赖模块STDM中，将原始观测流量数据输入到嵌入层中编码为初始特征表示并利用注意力机制和LSTM网络从初始特征表示中提取和融合时空特征，之后通过图注意力网络在邻居智能体间不断交换各自的时间状态特征表示$z_{1, t}、z_{2, t}、\cdots 、z_{i, t}、\cdots 、z_{|\mathcal{N}|, t}$来共享它们的观测值和状态表示。多智能体之间通过这种信息共享，能够更快以及更有效地达成全局共识，从而有效提升多智能体强化学习的性能。同时，通过STDM模块，即使n_i在独立执行策略μ_i时仍然能够包含来自其他所有智能体的全局时空信息，从而使得多智能体之间能够更有效地进行协同与合作；2)将STDM处理得到的时空特征状态作为初始输入，应用到基于集中训练分散执行架构的多智能体强化学习算法中，其中每个智能体n_i维护独立Actor网络μ_i以及集中式Critic网络Q_i^μ(o, a)，同时每个智能体n_i的分布式执行Actor网络μ_i由其各自的参数θ_i所决定，分布式执行策略μ_i的训练依赖于集中式Critic网络Q_i^μ(o, a)，从而进一步提高各智能体之间的协作能力。

4.1 智能体设计 4.1.1 观测空间

在道路网络中，排队长度和等待时间可以在空间上反映拥堵情况，相位可以在时间上反映在整个信号周期中所处阶段。由于本文所定义的4方向交叉路口共含有12个进口车道，因此，智能体n_i在时刻t的原始观测数据o_{i, t}定义为

$ o_{i, t}=\left\{q_{i, t}^1, q_{i, t}^2, \cdots, q_{i, t}^{12}, w_{i, t}^1, w_{i, t}^2, \cdots, w_{i, t}^{12}, p_{i, t}^c, p_{i, t}^n\right\}, $

(2)

其中：p_{i, t}^c, p_{i, t}ⁿ∈{l₁, l₂, l₃, l₄}分别是智能体n_i在时刻t时所处相位以及下一个相位，q_{i, t}^k和w_{i, t}^k分别是智能体n_i时刻t进口车道k上的排队长度以及车辆等待时间，k∈{1, 2, …, 12}。

4.1.2 动作空间

每个智能体都有4个不同的预定义可选择的相位，对应于图 3所示的4个相位l₁、l₂、l₃和l₄。与大多通过控制相位顺序转换来改善交通状况的研究^[38]不同，本文直接调节相位时长，可更加灵活地调度交通灯时间^[39]。智能体n_i在时刻t的动作a_{i, t}定义为

$ a_{i, t}=\left\{m_1, m_2, m_3, m_4\right\}, $

(3)

其中: m₁、m₂、m₃和m₄分别代表在下一个周期中l₁、l₂、l₃和l₄的绿信比，m₁, m₂, m₃, m₄∈[g_min/P, g_max/P]。具体参数设置见第5章实验部分。

4.1.3 奖励函数

本文将奖励定义为交叉路口各进口车道排队长度平方总和的负值，可以直观化地反映当前交叉路口的拥堵程度。智能体n_i在时刻t的奖励r_{i, t}定义为

$ r_{i, t}=-\sum\limits_{k=1}^{12}\left(q_{i, t}^k\right)^2, $

(4)

求和后取负值表示排队长度越长越应该被惩罚。

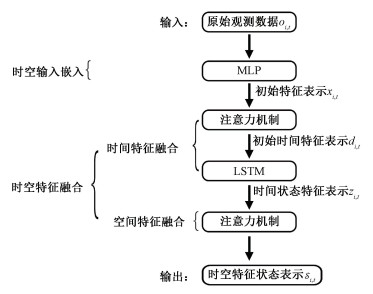
4.2 时空依赖模块STDM

时空依赖模块总共包含时空输入嵌入和时空特征融合两部分，如图 5所示。时空输入嵌入部分将原始观测数据编码为初始时空特征表示，时空特征融合部分由时间特征融合和空间特征融合组成。

在时间特征提取中，同时使用自注意力机制和LSTM有助于捕捉序列数据中的不同层次和长依赖关系。自注意力机制能够有效捕捉不同位置之间的关系和全局上下文信息，而LSTM通过门控机制专注于处理临近时间步之间的长依赖，提高序列建模的能力。在空间特征提取中，使用注意力机制中的优势在于其能够有效建模复杂的空间关系、实现自适应特征交互、多尺度特征提取，并结合上下文信息，从而增强对地理空间数据的特征理解和分析能力。时空依赖模块STDM通过邻居智能体之间不断地交换并共享信息，最终所获取的时空特征状态不但能够包含智能体自身的观测与动作信息，同时会包含其他所有智能体的全局时空依赖信息。通过这种信息共享，多智能体之间能够更快以及更有效地达成全局共识，从而有效提升多智能体强化学习的性能。

4.2.1 时空输入嵌入

时空输入嵌入旨在将时空输入数据编码为初始时空特征表示。给定智能体n_i在时刻t下的原始观测数据o_{i, t}及其动作a_{i, t}，将其经过多层感知机(multi-layer perceptron, MLP)f_x嵌入到初始特征表示x_{i, t}中，计算过程如下

$ x_{i, t}=f_x\left(o_{i, t}, a_{i, t}\right), $

(5)

f_x的具体参数设置见第5节实验部分。

4.2.2 时空特征融合

时空特征融合包括时间特征融合和空间特征融合2个维度，具体如下：

1) 时间特征融合

时间特征融合包括自注意力层和LSTM层，其目的是捕捉时间依赖性来融合不同时刻的时间特征。具体操作流程为：首先，自注意力层通过自注意力机制来计算2个不同时刻之间的相关性以捕捉全局上下文信息，从而生成考虑历史时刻1, 2, …, t-1影响的每个时刻t的加权的值向量作为初始时间状态特征表示; 然后，将初始时间状态特征表示作为输入，经过LSTM层进行序列建模，利用LSTM的递归门控机制捕捉长序列和长期依赖关系，得到更丰富的时间特征表示。通过这种顺序安排，自注意力机制优先处理序列内部的关联，然后LSTM层进一步对这些关联进行建模，有助于提取更具有信息丰富性的时间特征，以支持后续的任务。具体如下：

自注意力层：将输入的特征表示向量x_{i, t}通过3个不同的矩阵Q, K和V，得到不同表示形式的线性投影矩阵。计算智能体n_i在当前时刻t时来自历史时刻1, 2, …, t-1的信息相关性以及注意力权重，最终得到结合其余时刻影响的时刻t初始时间状态特征表示d_{i, t}，具体的计算过程如下

$ d_{i, t}=\operatorname{ReLU}\left(\boldsymbol{W}_V \sum\limits_{p=1}^{t-1} \alpha_{i, t, p} x_{i, p}+\boldsymbol{b}_V\right), $

(6)

α_{i, t, p}的计算过程如下

$ \alpha_{i, t, p}=\frac{\exp \left(\left(\boldsymbol{W}_Q x_{i, t}\right)^{\mathrm{T}} \boldsymbol{W}_K x_{i, p}\right)}{\sum_{q=1}^{t-1} \exp \left(\left(\boldsymbol{W}_Q x_{i, t}\right)^{\mathrm{T}} \boldsymbol{W}_K x_{i, q}\right)}, $

(7)

其中: p, q∈{1, 2, …, t-1}，x_{i, t}、x_{i, p}和x_{i, q}分别为智能体n_i在时刻t、p和q下的初始特征表示，W_Q、W_K和W_V为权重参数矩阵，b_V为偏置向量，d_{i, t}是智能体n_i在时刻t下的初始时间状态特征表示。

LSTM层：LSTM网络可用于建模长短期依赖关系，可以有效学习交通流量的长期和短期趋势以及捕获隐藏在数据中的周期性模式。输入门的计算公式为

$ g_{i, t}=\sigma\left(\boldsymbol{W}_g \times\left[h_{i, t-1}, d_{i, t}\right]+\boldsymbol{b}_g\right), $

(8)

其中: g_{i, t}是输入门的输出，W_g和b_g分别是输入门的权重矩阵和偏置向量，h_t-1是前一个时刻t-1的隐藏状态，d_{i, t}是当前时刻t的输入，σ是sigmoid激活函数。遗忘门的计算公式为

$ f_{i, t}=\sigma\left(\boldsymbol{W}_f \times\left[h_{i, t-1}, d_{i, t}\right]+\boldsymbol{b}_f\right), $

(9)

其中: f_{i, t}是遗忘门的输出，W_f和b_f分别是遗忘门的权重矩阵和偏置向量。根据当前的细胞状态和输入来确定输出值，输出门计算公式为

$ y_{i, t}=\sigma\left(\boldsymbol{W}_y \times\left[h_{i, t-1}, d_{i, t}\right]+\boldsymbol{b}_y\right), $

(10)

其中: y_{i, t}是遗忘门的输出，W_y和b_y分别是遗忘门的权重矩阵和偏置向量。

对于每个时刻t，LSTM接收输入d_{i, t}和前一时刻的隐藏状态h_{i, t-1}，然后计算3个门的状态和候选细胞状态。候选细胞状态的计算过程如下

$ \widetilde{c_{i, t}}=\tanh \left(\boldsymbol{W}_c \times\left[h_{i, t-1}, d_{i, t}\right]+\boldsymbol{b}_c\right), $

(11)

其中: W_c和b_c分别是候选细胞状态的权重矩阵和偏置向量，tanh(·)是双曲正切函数。然后，更新细胞状态c_t和隐藏状态h_t的计算过程如下

$ c_{i, t}=f_{i, t} \odot c_{i, t-1}+v_{i, t} \odot \widetilde{c_{i, t}}, $

(12)

$ h_{i, t}=y_{i, t} \odot \tanh \left(c_{i, t}\right), $

(13)

其中: c_{i, t}是当前时刻t的细胞状态，⊙表示点积运算，f_{i, t}用于遗忘前一时刻的细胞状态，v_{i, t}用于将新的候选细胞状态融合到当前细胞状态中，h_{i, t}是当前时刻的隐藏状态，y_{i, t}控制从细胞状态中提取的信息量。最终智能体n_i的输出时间状态特征表示z_{i, t}为

$ z_{i, l}=\operatorname{ReLU}\left(\boldsymbol{W}_l h_{i, l}+\boldsymbol{b}_l\right), $

(14)

其中: W_l和b_l分别是输出预测的权重矩阵和偏置向量。上述过程以d_{i, 1}为起点重复进行直至d_{i, t}为止。智能体之间不断交换共享所生成的时间状态特征表示z_{i, t}，以用于下一步的空间特征融合。

2) 空间特征融合

空间特征融合旨在融合道路网络中不同交叉路口之间的空间结构特征，使得每个交叉路口与邻居交叉路口共享信息。给定智能体n_i及其某个邻居交叉路口$n_j \in \mathcal{N}_i$，首先计算两者之间的关联度，然后将$\mathcal{N}_i$的特征表示及其对应的相关性结合，可以生成智能体n_i的时空特征状态表示$\mathcal{S}_{i, t}$。具体过程如下所示：

$ E_{i, j, t}=\boldsymbol{W}_{K^{\prime}} \boldsymbol{z}_{j, t}\left(\boldsymbol{W}_{Q^{\prime}} z_{i, t}\right)^{\mathrm{T}}, $

(15)

$ \beta_{i, j, t}=\frac{\exp \left(E_{i, j, t}\right)}{\sum_{n \in N_i} \exp \left(E_{i, n, t}\right)}, $

(16)

$ \mathcal{S}_{i, t}=\operatorname{ReLU}\left(\boldsymbol{W}_{V^{\prime}} \sum\limits_{j \in N_i} \beta_{i, j, t} z_{i, t}\right)+\boldsymbol{b}_{V^{\prime}}, $

(17)

其中: W_Q、W_K和W_V为权重参数矩阵，b_V′为偏置向量，E_{i, j, t}表示相邻交叉路口j对当前交叉路口i的影响，β_{i, j, t}是将E_{i, j, t}进行softmax函数归一化后的值。

上述时空依赖模块所获取的时空特征状态$\mathcal{S}_{i, t}$不但包含自身的观测与动作信息，同时也包含其邻居智能体的观测、动作以及相互间的时空依赖信息。将时空特征状态表示$\mathcal{S}_{i, t}$作为多智能体强化学习训练的输入，可有效提升智能体之间的协同能力。因此，智能体n_i的策略可看作μ_θi($\mathcal{S}_{i, t}$)，而智能体n_i的Q函数可看作Q_i^μ(o, a) =Q_i^μ($\mathcal{S}_{i, t}$)。时空依赖模块中的多种权重参数将在多智能体强化学习训练过程中同时得到训练。

4.3 算法设计

本节详细给出STLight算法的训练过程。基于上一小节所提出的时空依赖模块，将基于CTDE架构的多智能体强化学习算法^[40]应用于多路口的交通信号协同控制，该架构也是当前多智能体强化学习解决环境不稳定性的经典方法^[21]。CTDE框架在算法中的工作流程如下：在训练过程中，各智能体分别收集经验并将其传输至集中训练模块，通过集中式的方式计算共享的价值函数和策略改进梯度，从而协同优化智能体的策略和价值函数; 而在分布式执行阶段，每个智能体根据自身观测使用训练好的策略进行决策并执行相应的动作。如图 4 及算法 1 所示, 在训练阶段, 每个智能体 n_i 的集中式 Critic 网络Q_i^μ(o, a)需要接收来自所有智能体的信息，这体现在Critic Q_i^μ(o, a) 的定义依赖于所有智能体的联合观察o、联合动作a以及联合策略μ。而在实际执行阶段，每个智能体n_i根据自己学到的策略μ_i独立地采取行动。算法主要训练步骤如下：

① 获取原始观测数据o；

② 智能体n_i根据当前策略μ_θi选择其动作a_i；

③ 执行联合动作$\boldsymbol{a}=\left\{a_1, a_2, \cdots, a_{|\mathcal{N}|}\right\}$，获得即时奖励r和新原始观测值o′。将当前经验(o, a, r, o′)存储在经验回放区$\mathcal{D}$中；

④ 从经验回放缓冲区随机抽取S个样本；

⑤ 邻居智能体之间交换时间状态特征表示z_{i, t}；

⑥ 更新评论家网络参数，具体过程如下式所示

$ \mathcal{L}\left(\theta_i\right)=\mathbb{E}_{\boldsymbol{o}, \boldsymbol{a}, r, \boldsymbol{o}^{\prime}}\left[\left(y^i-Q_i^{\boldsymbol{\mu}}(\boldsymbol{o}, \boldsymbol{a})\right)^2\right], $

(18)

其中yⁱ的计算过程为

$ y^i=r_i+\left.\gamma Q_i^{\boldsymbol{\mu}^{\prime}}\left(\boldsymbol{o}^{\prime}, \boldsymbol{a}^{\prime}\right)\right|_{\boldsymbol{a}^{\prime}-\boldsymbol{\mu}^{\prime}}, $

(19)

⑦ 更新演员网络参数，具体过程如下式所示

$ \nabla_{\theta_i} J\left(\mu_i\right)=\mathbb{E}_{\boldsymbol{o}, \boldsymbol{a} \sim \mathcal{D}}\left[\left.\nabla_{\theta_i{\mu_{\theta_i}}} \nabla_{a_i} Q_i^\mu(\boldsymbol{o}, \boldsymbol{a})\right|_{a_i \leftarrow \mu_{\theta_i}}\right], $

(20)

⑧ 更新每个智能体n_i的目标网络参数，具体过程如下式所示

$ \theta_i^{\prime} \leftarrow \tau \theta_i+(1-\tau) \theta_i^{\prime} . $

(21)

STLight算法的训练流程如算法1所示。

算法1 STLight算法训练流程
1：初始化经验回放缓冲区$\mathcal{D}$、奖励折扣系数γ；
2：初始化每个智能体ni的策略参数θi和目标网络参数θ′i;
3：for each time t do
4：  for each $n_i \in \mathcal{N}$ do
5：      $a_i \leftarrow \mu_{\theta_i} ;$
6：  end for
7：执行联合动作$\boldsymbol{a}=\left\{a_1, a_2, \cdots, a_{|\mathcal{N}|}, \right.$
8：  获得即时奖励r和新原始观测值o′；
9：  $\mathcal{D} \leftarrow \mathcal{D} \cup\left\{\left(\boldsymbol{o}, \boldsymbol{a}, r, \boldsymbol{o}^{\prime}\right)\right\};$
10：  从$\mathcal{D}$随机抽样S个样本
11：    for each $n_i \in \mathcal{N}$ do
12：      邻居智能体之间交换zi, t；
13：      更新联合Q网络，见式(18)和式(19)。
14：      更新独立策略网络，见式(20)。
15：      更新目标网络参数，见式(21)。
16：    end for
17：end for

5 仿真实验

本节将STLight方法与已有工作进行比较来评估其性能。

5.1 实验设置

本文的仿真实验在城市交通模拟(simulation of urban mobility, SUMO)^[41]平台上进行，模拟器向信号控制方法提供状态并执行来自控制方法的交通信号动作，每次绿灯信号之后依次是3 s的黄灯信号时间以及2 s的红灯信号时间。实验场景为3×3道路网络和4×4道路网络，分别包含9和16个交叉路口，每个交叉路口的系统模型如图 2所示，2个相邻交叉路口之间的距离为200~1 000 m之间随机生成的值。本文采用随机速率来实时生成道路网络的交通流量^[42]，所生成车辆的平均速度为40 km/h^[43]，车辆左转、直行和右转的比例分别为30 %、60 % 和10 %，交通流量在仿真实验结束之前在所设定的道路网络中保持随机行驶^[43]。

μ_θi和Q_i^μ的神经网络结构为双层前馈神经网络，2层神经元数目分别为256和128。MLPf_x的层数为3，神经元数目为64。激活函数均为ReLU。具体实验训练参数设置如表 1所示。

5.2 对比方法与评估指标

将STLight与以下3种基于深度强化学习的TSC方法进行对比与评估：1)CoLight^[9]；2)STMARL^[33]；3)基于QMix^[32]的多路口TSC方法，记作QMix。为验证所提算法中每个环节的效用，除以上基线方法之外，我们还考虑了STLight的几种变体：1)去除时空依赖模块的STLight方法，记作STLight without STDM；2)去除时间特征融合部分的STLight方法，记作STLight without Temporal；3)去除空间特征融合部分的STLight方法，记作STLight without Spatial。通拥塞率^[43]作为性能指标来分别评估所有方法、基线方法以及变体方法的性能^[9]。等待时间为一辆车处于排队状态所占用的总时间，将行驶经过交叉路口所有车辆的等待时间取平均值，即可得到平均等待时间。交通拥塞率为排队长度大于10的时间与仿真实验总时间的比值。

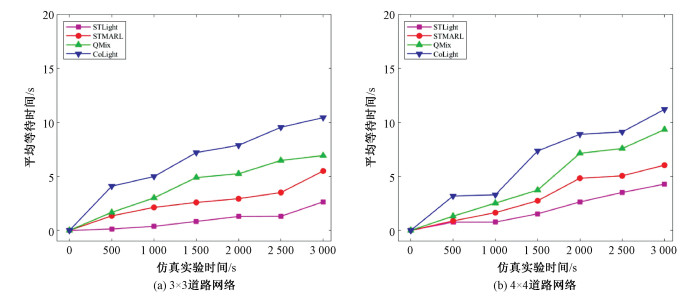
5.3 实验结果及分析

3×3道路网络场景下基线方法以及STLight的平均等待时间如图 6(a)所示。在仿真实验的初始阶段，STLight的车辆平均等待时间增长相对缓慢。随着时间的增长，道路网络中的交通流量不断增多，因此平均等待时间也随之增多。总体来看，4种方法的平均等待时间增长速度从低到高依次为：STLight、STMARL、QMix和CoLight。具体来说，与CoLight相比，STLight将性能平均提升约39.67 %；与QMix相比，STLight将性能平均提升约26.25 %；与STMARL相比，STLight将性能平均提升约18.64 %。4×4道路网络场景下不同算法的平均等待时间如图 6(b)所示。不同于3×3道路网络场景，在仿真实验刚开始的阶段，与其他实验方法相比，CoLight的平均等待时间有较为明显的增长。而随着时间的增长，尽管基线方法的平均等待时间增长相对于3×3道路网络场景较为稳定，但其平均等待时间相对于STLight方法依然较高，且STLight的平均等待时间始终保持在稳定且较低的增长速度。与CoLight相比，STLight将性能平均提升约34.32 %；与QMix相比，STLight将性能平均提升约23.08 %；与STMARL相比，STLight将性能平均提升约16.45 %。可以看出，在3×3道路网络场景下，STLight相较于其他方法的性能提升效果比4×4道路网络场景更为显著。随着交通流量的增多，传统多智能体强化学习方法以及不考虑各交叉路口间时空依赖性的强化学习方法性能明显下降。STLight方法相较基线多智能体强化学习方法STMARL存在一定优势，原因在于STLight使用基于CTDE架构的多智能体强化学习，CTDE结合全局优化与本地灵活执行的优点，既充分发挥了集中资源共享和协同学习的优势，又保留了分散系统的响应速度和可扩展性。

3×3道路网络场景下STLight方法及不同变体的交通拥塞率如图 7(a)所示。与STLight without STDM相比，STLight将性能平均提升约25.15 %；与STLight without Spatial相比，STLight将性能平均提升约12.65 %；与STLight without Temporal方法相比，STLight将性能平均提升约18.69 %。4×4道路网络场景下不同算法的交通拥塞率如图 7(b)所示。在道路网络规模增大的情况下，所有方法的性能相比于3×3道路网络场景有可忽略不计的轻微下降，但STLight依然是性能最优的方法。具体来说，与STLight without STDM相比，STLight将性能平均提升约27.86 %；与STLight without Spatial相比，STLight将性能平均提升约12.33 %；与STLight without Temporal方法相比，STLight将性能平均提升约22.43 %。可以看出空间特征融合部分比时间特征融合部分更有效，同时时空依赖模块STDM可以捕获各交叉路口间的时空依赖关系，有助于增强各智能体之间的协作能力，从而提升多路口TSC的性能。

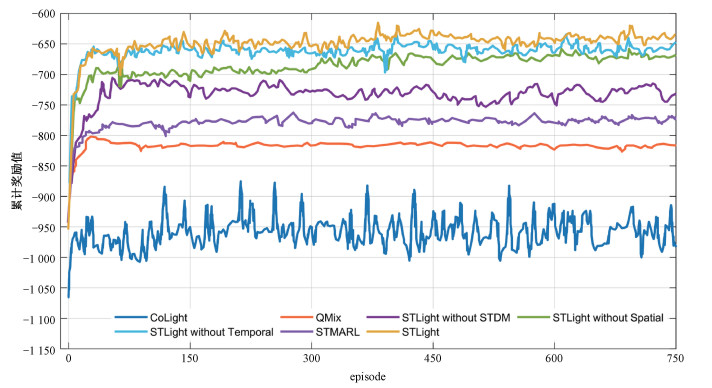
所有实验方法的累计奖励值学习曲线如图 8所示。无论是在初始探索阶段还是在最终收敛阶段，STLight的性能都优于所有变体以及基线方法。CoLight学习曲线波动幅度较大，经过较长时间的训练后趋于收敛，原因是CoLight为状态和动作维度较大的单智能体强化学习算法，在高维联合动作空间上进行策略学习时会面临可扩展性问题。相比之下，QMix和STMARL等多智能体强化学习方法能够更加快速地收敛到全局最优解，但其性能仍然与STLight及其变体存在差距。除此之外，STLight without STDM、STLight without Spatial以及STLight without Temporal均取得良好的学习效果，且收敛速度较快。

所有实验方法的平均累积奖励结果如表 2所示，其中最优值在表格中用粗体标出。在3×3道路网络和4×4路网场景中，STLight方法的平均累积奖励分别比CoLight高出312和555，性能提升32.91 % 和31.86 %；STLight方法的平均累积奖励分别比QMix高出187和344，性能提升22.72 % 和22.47 %；STLight方法的平均累计奖励分别比STMARL高出239和304，性能提升17.94 % 和20.39 %；STLight方法的平均累计奖励分别比STLight without STDM方法高出102和199，性能提升13.82 % 和14.36 %；STLight方法的平均累计奖励分别比STLight without Temporal方法高出47和80，性能提升6.88 % 和6.31 %；STLight方法的平均累计奖励分别比STLight without Spatial方法高出61和58，性能提升9.93 % 和4.66 %。原因是STLight利用时空依赖模块STDM和集中训练分散执行框架的多智能体强化学习算法，有效地提高了各交叉路口之间的协作能力，即使在道路网络规模增大的情况下依然能够维持道路网络交通信号控制系统的基本运转，缓解交通拥堵现象。

6 总结

本文针对城市交通拥堵问题，将多路口交通信号控制转化为马尔可夫博弈问题，提出一种基于时空依赖关系多智能体强化学习的多路口交通信号协同控制方法STLight。STLight利用时空依赖模块STDM来提取多交叉路口交通流量的时空依赖关系，并结合集中训练分散执行的多智能体强化学习算法进行高效的交通信号协同控制工作。仿真结果表明，与现有算法相比，STLight在提升城市道路网络的性能方面具有显著的优势，有助于缓解当前城市交通拥堵问题。