2. 西安交通大学航天学院 机械结构强度与振动国家重点实验室, 西安 710049
2. State Key Laboratory for Strength and Vibration of Mechanical Structures, School of Aerospace, Xi'an Jiaotong University, Xi'an 710049, China
当液滴撞击高温过热固壁时,液滴下表面会发生剧烈的沸腾,形成的蒸汽层将液滴托起,使其无法与壁面发生接触,这就是著名的莱顿弗罗斯特效应(Leidenfrost effect)[1]。由于气相的导热率远低于液相和固相的导热率,发生Leidenfrost碰撞时会极大地影响液滴与固壁之间的换热效率,因此在诸如喷雾冷却[2]和内燃机中燃料喷射[3]等许多工业应用中都希望避免出现这一现象,这也促进了人们对Leidenfrost效应的关注和研究[4-5]。
同时,由于液滴与固壁表面没有直接接触,这也极大地减小了液滴运动时受到的摩擦阻力[6],使得液滴具有很好的移动性。这一特征使得我们可以采用无接触的方式控制液滴运动,因而Leidenfrost现象也受到微纳米流体控制领域的关注。但在缺少摩擦力的情况下,Leidenfrost液滴不仅会因壁面轻微的倾斜而滑动[7],还会出现弹跳[8-9]、振荡[10-13]等复杂的动力学过程,这对液滴控制是一个很大的挑战。Linke等[14]发现,当落在具有非对称表面纹理(如棘齿)的过热固壁上时,Leidenfrost液滴可以在某一方向上以数十cm/s的速度自行向前推进,这一方法可以有效地引导悬浮液滴[15-16]或固体[17-18]在固体表面运动。
相比于液滴和高温过热固体表面的作用,在高温液体表面同样存在着Leidenfrost效应[19-21]。当Leidenfrost液滴悬浮在液池表面时,液池表面会因重力的作用而显著变形,从而抑制因烟囱效应产生的不稳定性[22],使得液池相比固壁能够承受并维持更大的液滴。此外由于液池的表面粗糙度可忽略不计,因此Leidenfrost状态可以在更低的表面过热度工况下维持[19]。然而,液体表面的可变形性以及其内部存在流动等特点使得问题更复杂,同时控制液滴运动存在更大的难度。目前已有的实验[23-25]已经观察到悬浮液滴会在过热液池表面滑行数秒。根据Gauthier等[26]的模型预测,液滴会因其下方蒸汽膜厚度μm量级的不对称性而向某一方向自行推进。这种Leidenfrost液滴在加热的液体表面上的自推进行为有望成为一种在不接触液池本身或池壁的情况下输送各种尺寸液滴的方法,因而具有很大的研究价值。然而,在实验方面,由于很难清晰地观察液池内部的流动状态,目前还无法定量描述其对于液滴自推进过程的影响,而数值模拟及理论方面的工作则更多地集中在对液滴稳定工况的分析[19, 27-28],对液滴和液池内部瞬态流动的研究很少,因此本研究拟从直接数值模拟的角度展开对该问题的初步分析。
本文主要研究乙醇液滴落入高温硅油液池并与其接触时液池内部流动状态的演变,其中重点关注液池表面马兰戈尼效应(Marangoni effect)的作用效果。通过分析液池内部流动状态以及界面附近的传热传质特征,为液滴自推进过程的分析提供一些依据。
1 控制方程对于含气液相变的不可压缩两相流动,连续性方程和动量方程分别为
| $\nabla \cdot \boldsymbol{u}=\left(\frac{1}{\rho_{\mathrm{g}}}-\frac{1}{\rho_1}\right) \dot{m} \delta_{\mathrm{s}}, $ | (1) |
| $\begin{gathered}\rho\left(\frac{\partial \boldsymbol{u}}{\partial t}+\boldsymbol{u} \cdot \nabla \boldsymbol{u}\right)=-\nabla p+\nabla \cdot\left(\mu\left(\nabla \boldsymbol{u}+\nabla \boldsymbol{u}^{\mathrm{T}}\right)\right)+ \\ \rho \boldsymbol{g}+\sigma \kappa \delta_{\mathrm{s}} \boldsymbol{n}+\delta_{\mathrm{s}} \nabla_{\mathrm{s}} \sigma, \end{gathered}$ | (2) |
其中: u为流体速度(m/s),p为压力(Pa),ρ为密度(kg/m3),μ为动力黏度(Pa·s),g为重力加速度(m/s2),
由于气液相变依赖流动传热过程,因此能量守恒方程也需要进行求解
| $\rho c_p\left(\frac{\partial T}{\partial t}+u \cdot \nabla T\right)=\nabla \cdot(\lambda \nabla T), $ | (3) |
其中: T为温度(K),cp为定压比热容(J/(kg·K)),λ为导热系数(W/(m·K))。
2 数值方法本文采用直接数值模拟的方法研究Leidenfrost相变过程,其数值方法已在文献[30]中公开发表,这里不再赘述。简单而言,通过在笛卡尔网格上应用有限体积法离散控制方程,采用时间层交错的近似投影方法[31]求解不可压缩Navier-Stokes方程,其中对流项采用二阶精度的Bell Colella Glaz(BCG)格式[32]进行离散,扩散项应用全隐格式进行离散。对于多相流动问题,采用VOF方法(volume of fluid)[33]捕捉气液界面,借助界面几何重构技术既保证界面在推进过程中流体体积的守恒性,又确保界面能够始终维持陡峭形式,不会出现耗散。此外,通过应用基于四叉树/八叉树的自适应网格技术,仅在界面附近和高涡量的区域细化网格,从而大幅提升计算效率。
2.1 表面张力的计算在多相流动问题中,表面张力计算的准确性对于界面运动过程尤为重要。本文采用连续表面力模型[29],将表面张力转化为体积力的形式加入动量方程中进行求解。其中计算法向表面张力时,可借助VOF方法中定义的体积分数f,将表面张力近似为σκδsn≈
为考虑当前问题中存在的Marangoni效应,表面张力系数σ不再是常数,其值也取决于局部温度场并产生切向梯度,因而还需要计算切向表面张力项。本文假定表面张力系数与当地温度线性相关,即
| $\sigma=\sigma_0-\sigma_T\left(T-T_{\text {ref }}\right), $ | (4) |
其中:σ0为参考温度Tref下的表面张力系数,σT为常系数。当界面温度已知时,界面上各处的表面张力系数即可通过式(4)计算得到,之后采用基于高度函数的方法[37-38]计算界面切向表面张力梯度。
2.2 相变模型液滴表面的蒸发效应对于Leidenfrost现象是必不可少的,采用最近发展的气液相变算法[30]来计算液滴的蒸发过程。尽管发生相变时依旧可以认为界面处的温度场是连续的,但界面质量通量的存在必然会导致界面两侧的热通量出现间断
| $\dot{m}=\frac{\left((\lambda \nabla T)_1-(\lambda \nabla T)_{\mathrm{g}}\right) \cdot \boldsymbol{n}}{\mathcal{L}}$ | (5) |
其中:
为在计算过程中维持能量守恒,结合嵌入边界法和有限体积法的优势,通过在界面处施加适当的Dirichlet边界条件,使得气液两相的温度场可以分开求解。这种方法的优势在于能量守恒方程(3)中不需要添加额外的源项来考虑相变的影响,因而可以计算得到气液界面附近准确的温度场信息,并有助于获得准确的界面质量通量。
在本文研究的问题中,由于存在液滴-气体和液池-气体2个界面,而相变只出现在液滴表面上,因此需要采用2个VOF函数分别捕捉不同的界面,从而区分2类界面。此外,由于液滴将长时间悬浮于温度高于自身沸点的液池表面,因此忽略液滴内部的温度场演化过程,假设液滴温度始终保持在饱和温度,气相温度场在液滴界面的边界条件即为Tg, Γ=Tsat。
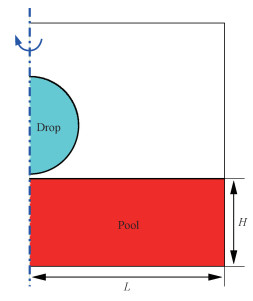
3 数值结果 3.1 计算模型如图 1所示,本文中的数值模拟均采用轴对称坐标系进行,初始直径为d0=2.256 mm的球形液滴在重力的作用下朝着宽度和深度分别为L=10 d0和H=8 d0的过热液池下落。液滴和液池分别由乙醇和硅油构成,由于硅油的沸点远高于乙醇,且不易挥发,因此这样一组工质可以确保在高温环境下只有液滴表面发生相变产生蒸汽。
|
Download:
|
| 图 1 计算模型示意图 Fig. 1 Computation model | |
首先,为验证当前使用的数值算法可以准确地求解此类Leidenfrost问题,将数值结果与Maquet等[19]提出的理论模型进行比较。该理论模型基于静力平衡假设,在恒定液相温度的情况下预测了液滴与液池界面的平衡状态,因此设定计算过程中液滴和液池温度分别始终保持在Tdrop=Tsat=351 K和Tpool=391 K,对应过热度T=40 K的工况,相应的流体物性参数如表 1所示。
|
|
表 1 乙醇和硅油的物性参数 Table 1 Physical properties of the ethanol and silicon oil |
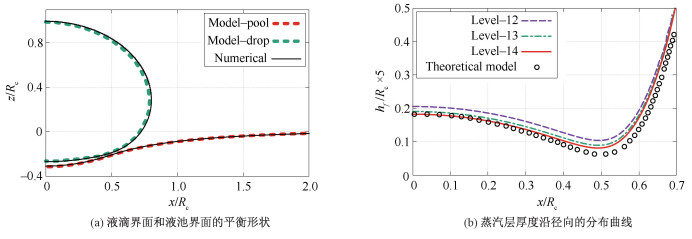
从理论模型中可知,对于半径R~O(1 mm)的液滴,蒸汽层的厚度约为h~O(20 μm),为完全解析蒸汽层内的流动,验证3种网格分辨率下Δx=3.3、1.65及0.826 μm的数值结果,分别对应12、13和14层网格。在当前问题中,由于最小网格尺度与计算区域尺度相差4个量级,需要采用自适应网格技术提高计算效率,仅在接近界面的区域应用最细的网格,而其他区域采用较粗网格即可。数值模拟结果如图 2所示。图 2(a)展示液滴与液池界面的平衡形态,描绘了液滴悬浮在高温液池上方的情景。由于硅油液池的温度高于乙醇液滴的饱和温度,在这种情况下,液滴底部与液池表面之间因相变产生的一层薄蒸汽膜将两者持续分离开,无法相互接触。从整体形态来看,不同网格分辨率下的结果均与理论模型结果吻合良好。由于蒸汽层厚度远小于液滴半径,图 2(b)进一步展现了蒸汽层的厚度分布结果,可以看到当采用最高的网格分辨率时,数值结果已经非常接近理论结果,由此验证了当前应用的数值算法的准确性。此外,由于液滴在该过热度工况下悬浮500 ms的过程中,液滴体积仅减小约1.5%,因此我们认为液滴体积变化对结果的影响可以忽略。
|
Download:
|
| 图 2 数值结果与理论模型的对比 Fig. 2 Comparisons of the numerical results against the theoretical solutions | |
在上一小节的数值验证中,为与理论模型的结果进行对比,忽略了液池温度随时间的变化。为研究液池表面的Marangoni效应,从本节开始,初始液池过热度依旧为ΔT=40 K,但液池温度不再恒定不变,将受到上方液滴的影响发生变化。液池表面张力系数与当地温度线性相关,满足式(4),其中σT=5×10-5 N/(m·K)。此外其他物性参数均不随温度发生变化,由表 1给出。
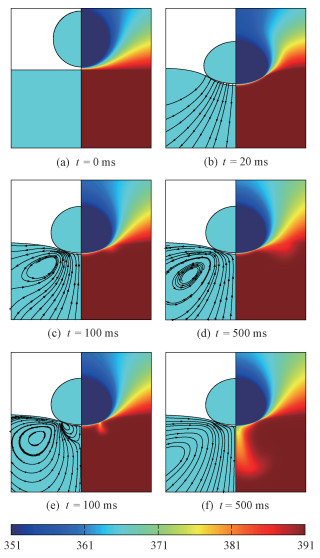
图 3展示了液滴撞击过热液池并反弹的过程中,流场以及温度场的演化过程。当不考虑液池表面的Marangoni效应时,从图 3(a)~3(d)中可以看到,液滴在撞击液池的过程中发生了显著变形,由于液滴的半径小于其毛细特征长度Rc=
|
Download:
|
| 图 3 Leidenfrost液滴撞击液池的过程,有无Marangoni效应2种情况下,不同时刻的流场流线图(左)和温度场云图(右) Fig. 3 The Streamlines (left) and temperature field (right) at different moments during the process the Leidenfrost droplet impacting the liquid pool with or without Marangoni effect | |
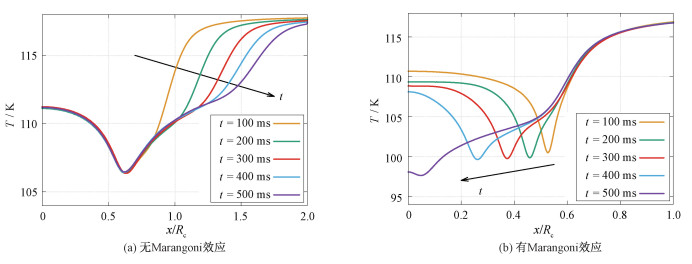
在整个模拟过程中,由于液滴底部蒸发产生的蒸汽持续向外逸出,蒸汽层内气体的流动会对液池表面施加沿径向向外的剪切应力,当液池表面的Marangoni效应忽略不计时,液池内部会在该剪切应力的影响下形成逆时针的环流,如图 3(c)和3(d)中左侧流线图所示。图 4(a)展示液池表面温度分布随时间的变化,在液滴刚开始撞击液池时,由于液池内部初始处于静止状态,高温液池的表面会受到上方低温液滴的影响,温度迅速下降,该过程在蒸汽层厚度最薄的位置表现尤为显著。随着液池内部环流的建立,在液池中心自下而上的流动大幅限制了界面附近的温度扩散过程,使得位于液滴下方(x/Rc<1)的液池表面温度不再继续下降并趋近于恒定状态,其中表面温度最低值位置始终处于蒸汽层厚度最薄处。因此可看出在没有Marangoni效应的情况下,液池内部的流动具有维持Leidenfrost效应的特点。
|
Download:
|
| 图 4 不同时刻液池表面的温度分布 Fig. 4 Temperature distribution of the liquid surface at different moments | |
当Marangoni效应加入到数值模拟中后,尽管液池表面依旧受到由蒸汽流动引起的沿径向向外的剪切应力作用,但因初始撞击导致的液池界面温度分布的不均匀使得表面张力分布出现差异,由此在液池界面处产生了额外的Marangoni应力。图 4(b)展示有Marangoni效应的情况下液池表面的温度分布,与先前情况类似,在最开始的液滴撞击和反弹阶段,蒸汽层最薄的地方热通量最大,温度下降最快,形成局部最低温度。由于表面张力随温度降低而增大,该位置也成为表面张力的最大值点,在该点内侧产生沿径向向外的Marangoni应力,外侧形成沿径向向内的Marangoni应力。从图 3(e)中t=100 ms时刻的流线图可以看到,沿径向向内的Marangoni应力诱导液池内部形成一个顺时针环流,明显抑制了由蒸汽剪切应力主导的逆时针环流,并在二者交汇处,即温度最低点形成一个“热射流”结构,如右侧温度场云图所示。随着时间的推移,由于液滴下方的流动受到阻碍,在热扩散的影响下液池界面温度持续下降,进一步扩大了内外温差以及Marangoni应力沿径向向内的合力,因此温度最低点和“热射流”不断向内移动,最终在液池中心形成下沉的热羽流,如图 3(f)中t=500 ms时刻所示。
在上述液池流动状态的转变过程中,液池表面受到气体流动引起的剪切应力和温度梯度引起的Marangoni应力。基于量纲分析,液滴下表面蒸发所需要的能量近似等于液池经由蒸汽层通过导热传递过来的能量,因此总蒸发量为
| $\mu \frac{\partial u}{\partial z} \sim \mu \frac{U}{h} \sim \frac{\mu \lambda \Delta T R}{\rho_{\mathrm{g}} h^3 \mathcal{L}}.$ | (6) |
此外,由表面张力随温度变化的表达式(4)可知,液池表面Marangoni应力可表示为
| $\frac{\partial \sigma}{\partial r} \sim \sigma_T \frac{\Delta T}{R}.$ | (7) |
最后将物性参数代入上述2个应力表达式中,其中蒸汽层厚度可由数值模拟结果或理论模型结果获得,可估算得知在当前的工况下Marangoni应力比气体剪切应力大1个量级左右,因此Marangoni应力主导的顺时针环流会抑制气体剪切应力主导的逆时针环流,并最终形成与无Marangoni效应情况完全不同的流动形态。
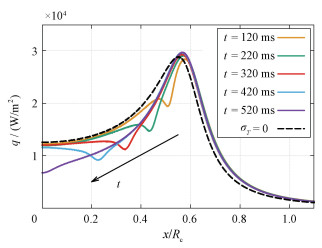
图 5进一步展示有无Marangoni效应2种情况下液池表面热通量分布。由于“热射流”位置处温度存在极小值,因此该区域也存在热流通量的极小值,并跟随“热射流”位置移动。从图中可看到与黑色虚线表示的无Marangoni效应情况相比,“热射流”以外的区域热通量基本一致,而随着“热射流”向内移动,中心的热通量出现下降趋势。此过程中,热通量最大的位置几乎始终位于蒸汽层最薄位置处。
|
Download:
|
| 图 5 有无Marangoni效应2种情况下液池表面热通量分布 Fig. 5 The heat flux on the surface of the liquid pool with or without Marangoni effect | |
尽管有无Marangoni效应2种情况下液池的流动状态截然不同,但蒸汽层厚度却相差不到2 μm。从数值模拟结果中可看到,由于硅油液池的黏度远大于乙醇蒸汽的黏度,气体流出速度大约为0.5 m/s,而液池流动速度仅为5 mm/s,远小于气体流动速度,因此在表面热通量接近的情况下,界面运动对于蒸汽层内润滑压力的建立影响不大,蒸汽层厚度基本一致。此外,相比固壁而言,由于液池内部流动有助于维持表面温度以及热通量保持不变,这使得Leidenfrost状态能够持续更长的时间。
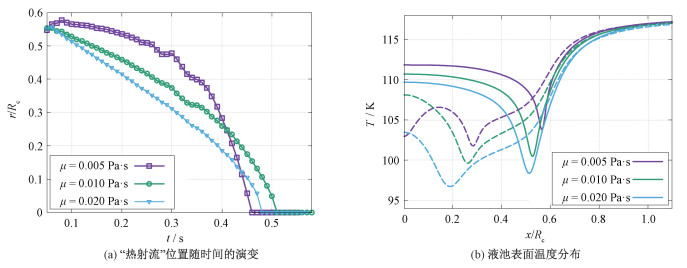
3.4 液池黏度对流动状态的影响当液池黏度发生变化时,液池内部流动状态的转变过程也发生了相应变化。图 6(a)展示μ=0.005,0.01,0.02 Pa·s这3种液池黏度情况下,“热射流”位置随时间的变化。经过最开始的撞击过程之后,界面很快在表面张力的作用下趋近稳定形态,在蒸汽层最薄处形成的“热射流”不断向内移动。随着液池黏度的增大,射流点沿径向向内的移动速度加快。结合图 6(b)中t=100 ms时刻的液池界面温度分布可知,液池黏度越大,液滴下方由气体剪切应力驱动的逆时针环流越弱,初始液池温度下降越快,由此产生的沿径向向内的Marangoni应力越大,从而加快了“热射流”向内推进的过程。
|
Download:
|
| 图 6 不同液池黏度的情况下,“热射流”位置和液池表面温度的变化 Fig. 6 The time evolution of the position of the "jet" and temperature distribution on the surface of the pool for different pool viscosities | |
然而对于较低黏度μ=0.005 Pa·s的液池而言,从图 6(a)中可看到虽然初始“热射流”移动速度较慢,但大约从t=300 ms时刻开始呈现加速的趋势,相比高黏度液池工况更早地形成最终的下沉热羽流。在图 6(b)中,实线和虚线分别表示t=100和400 ms的液池表面温度分布情况。可以看到在t=400 ms时,μ=0.01、0.02 Pa·s这2个高黏度液池工况的模拟结果中,液池表面仅存在一个温度极小值点,始终对应“热射流”区域。而在低黏度工况下的结果中发现,在液池中心处出现第2个温度极小值点,这使得液池中心区域在Marangoni效应的驱使下形成第2个顺时针环流,如图 7所示,并进一步削弱蒸汽剪切应力驱动的逆时针环流,这也就解释了“热射流”加速向内运动的原因。由于在其他液池黏度的算例结果中均不存在中心的第2个顺时针环流,说明该现象并非单纯由界面附近温度的对流扩散过程引发的。通过对比不同时刻界面的演化过程,发现初始液滴撞击形成的表面波经过一段时间的传播后,会从计算区域边界返回液滴附近,由此对界面产生的扰动使得液池表面热边界层失稳,因此在中心处出现第2个温度极小值点并促进第2个顺时针环流的形成。

|
Download:
|
| 图 7 t=300 ms时,液池黏度μ=0.005 Pa·s流线图(左)和温度场云图(右) Fig. 7 The streamline diagram (left) and temperature field (right) at the moment of t=300 ms with liquid pool viscosity of μ=0.005 Pa·s | |
综上所述,液池黏度增大后,一方面会削弱由气体流动驱动的逆时针环流,并增大内外温差,从而促使“热射流”更快地向内运动;另一方面较高的黏性会加快对撞击产生的表面波的耗散,减小界面扰动,同时中心受到抑制的环流还会使得界面附近热边界层增厚,所以在中心区域不易出现因界面失稳导致的第2个顺时针环流。
4 结论在当前的数值研究中,模拟Leidenfrost液滴撞击高温液池的过程,并再现液滴经过撞击反弹过程后在液池表面长时间悬浮的情景,即因液滴下表面不断蒸发而维持的薄气膜将液滴托起,使其无法与液池直接接触。从数值模拟结果中可以看到,Marangoni效应的存在对液池内部流场和温度场随时间演变的过程有很大影响,尤其会导致“热射流”的形成及其向下沉热羽流的转变。当Marangoni应力大于气体黏性剪切应力时,液池内“热射流”的移动过程会受到液池黏度的影响。一方面增大黏度会抑制逆时针环流,并加快液池表面温度的下降,促进Marangoni对流向内的推动作用;另一方面黏度也会加快对表面波的耗散,使得界面更加稳定,不易出现二次环流。通过对液池内部流动演化过程的分析,尤其是可能出现的表面不稳定性,有助于将来对液滴自驱动现象的深入研究。
| [1] |
Leidenfrost J G. On the fixation of water in diverse fire[J]. International Journal of Heat and Mass Transfer, 1966, 9(11): 1153-1166. Doi:10.1016/0017-9310(66)90111-6 |
| [2] |
Kim J. Spray cooling heat transfer: the state of the art[J]. International Journal of Heat and Fluid Flow, 2007, 28(4): 753-767. Doi:10.1016/j.ijheatfluidflow.2006.09.003 |
| [3] |
Moreira A L N, Moita A S, Panão M R. Advances and challenges in explaining fuel spray impingement: how much of single droplet impact research is useful?[J]. Progress in Energy and Combustion Science, 2010, 36(5): 554-580. Doi:10.1016/j.pecs.2010.01.002 |
| [4] |
Biance A L, Clanet C, Quéré D. Leidenfrost drops[J]. Physics of Fluids, 2003, 15(6): 1632-1637. Doi:10.1063/1.1572161 |
| [5] |
Quéré D. Leidenfrost dynamics[J]. Annual Review of Fluid Mechanics, 2013, 45: 197-215. Doi:10.1146/annurev-fluid-011212-140709 |
| [6] |
Vakarelski I U, Marston J O, Chan D Y C, et al. Drag reduction by Leidenfrost vapor layers[J]. Physical Review Letters, 2011, 106(21): 214501. Doi:10.1103/physrevlett.106.214501 |
| [7] |
Bouillant A, Mouterde T, Bourrianne P, et al. Leidenfrost wheels[J]. Nature Physics, 2018, 14(12): 1188-1192. Doi:10.1038/s41567-018-0275-9 |
| [8] |
Tran T, Staat H J J, Prosperetti A, et al. Drop impact on superheated surfaces[J]. Physical Review Letters, 2012, 108(3): 036101. Doi:10.1103/physrevlett.108.036101 |
| [9] |
Celestini F, Frisch T, Pomeau Y. Take off of small Leidenfrost droplets[J]. Physical Review Letters, 2012, 109(3): 034501. Doi:10.1103/PhysRevLett.109.034501 |
| [10] |
Brunet P, Snoeijer J H. Star-drops formed by periodic excitation and on an air cushion: a short review[J]. The European Physical Journal Special Topics, 2011, 192(1): 207-226. Doi:10.1140/epjst/e2011-01375-5 |
| [11] |
Ma X L, Burton J C. Self-organized oscillations of Leidenfrost drops[J]. Journal of Fluid Mechanics, 2018, 846: 263-291. Doi:10.1017/jfm.2018.294 |
| [12] |
Bergen J E, Basso B C, Bostwick J B. Leidenfrost drop dynamics: exciting dormant modes[J]. Physical Review Fluids, 2019, 4(8): 083603. Doi:10.1103/physrevfluids.4.083603 |
| [13] |
胡子豪, 任宁, 俞熹. 莱顿弗罗斯特水滴振荡模式的影响因素及机理探究[J]. 物理实验, 2018, 38(3): 32-37. Doi:10.19655/j.cnki.1005-4642.2018.03.009 |
| [14] |
Linke H, Alemán B J, Melling L D, et al. Self-propelled Leidenfrost droplets[J]. Physical Review Letters, 2006, 96(15): 154502. Doi:10.1103/physrevlett.96.154502 |
| [15] |
Cousins T R, Goldstein R E, Jaworski J W, et al. A ratchet trap for Leidenfrost drops[J]. Journal of Fluid Mechanics, 2012, 696: 215-227. Doi:10.1017/jfm.2012.27 |
| [16] |
庄峻杰. 高温锯齿表面形貌对Leidenfrost液滴运动影响的实验研究[D]. 北京: 华北电力大学, 2022. DOI: 10.27140/d.cnki.ghbbu.2022.000379.
|
| [17] |
Hashmi A, Xu Y H, Coder B, et al. Leidenfrost levitation: beyond droplets[J]. Scientific Reports, 2012, 2(1): 797. Doi:10.1038/srep00797 |
| [18] |
Dupeux G, Baier T, Bacot V, et al. Self-propelling uneven Leidenfrost solids[J]. Physics of Fluids, 2013, 25(5): 051704. Doi:10.1063/1.4807007 |
| [19] |
Maquet L, Sobac B, Darbois-Texier B, et al. Leidenfrost drops on a heated liquid pool[J]. Physical Review Fluids, 2016, 1(5): 053902. Doi:10.1103/physrevfluids.1.053902 |
| [20] |
Mogilevskiy E. Levitation of a nonboiling droplet over hot liquid bath[J]. Physics of Fluids, 2020, 32(1): 012114. Doi:10.1063/1.5131818 |
| [21] |
王浩, 徐进良. 油面上相邻Leidenfrost液滴的相互作用及运动机制[J]. 物理学报, 2023, 72(5): 226-237. Doi:10.7498/aps.72.20221822 |
| [22] |
Snoeijer J H, Brunet P, Eggers J. Maximum size of drops levitated by an air cushion[J]. Physical Review E, 2009, 79(3): 036307. Doi:10.1103/physreve.79.036307 |
| [23] |
Adda-Bedia M, Kumar S, Lechenault F, et al. Inverse Leidenfrost effect: levitating drops on liquid nitrogen[J]. Langmuir, 2016, 32(17): 4179-4188. Doi:10.1021/acs.langmuir.6b00574 |
| [24] |
Janssens S D, Koizumi S, Fried E. Behavior of self-propelled acetone droplets in a Leidenfrost state on liquid substrates[J]. Physics of Fluids, 2017, 29(3): 032103. Doi:10.1063/1.4977442 |
| [25] |
Matsumoto R, Hasegawa K. Self-propelled Leidenfrost droplets on a heated glycerol pool[J]. Scientific Reports, 2021, 11: 3954. Doi:10.1038/s41598-021-83517-1 |
| [26] |
Gauthier A, Diddens C, Proville R, et al. Self-propulsion of inverse Leidenfrost drops on a cryogenic bath[J]. Proceedings of the National Academy of Sciences of the United States of America, 2019, 116(4): 1174-1179. Doi:10.1073/pnas.1812288116 |
| [27] |
Van Limbeek M A J, Sobac B, Rednikov A, et al. Asymptotic theory for a Leidenfrost drop on a liquid pool[J]. Journal of Fluid Mechanics, 2019, 863: 1157-1189. Doi:10.1017/jfm.2018.1025 |
| [28] |
Sobac B, Maquet L, Duchesne A, et al. Self-induced flows enhance the levitation of Leidenfrost drops on liquid baths[J]. Physical Review Fluids, 2020, 5(6): 062701. Doi:10.1103/physrevfluids.5.062701 |
| [29] |
Brackbill J U, Kothe D B, Zemach C. A continuum method for modeling surface tension[J]. Journal of Computational Physics, 1992, 100(2): 335-354. Doi:10.1016/0021-9991(92)90240-Y |
| [30] |
Zhao S, Zhang J, Ni M J. Boiling and evaporation model for liquid-gas flows: a sharp and conservative method based on the geometrical VOF approach[J]. Journal of Computational Physics, 2022, 452: 110908. Doi:10.1016/j.jcp.2021.110908 |
| [31] |
Popinet S. An accurate adaptive solver for surface-tension-driven interfacial flows[J]. Journal of Computational Physics, 2009, 228(16): 5838-5866. Doi:10.1016/j.jcp.2009.04.042 |
| [32] |
Bell J B, Colella P, Glaz H M. A second-order projection method for the incompressible Navier-Stokes equations[J]. Journal of Computational Physics, 1989, 85(2): 257-283. Doi:10.1016/0021-9991(89)90151-4 |
| [33] |
Weymouth G D, Yue D K P. Conservative volume-of-fluid method for free-surface simulations on Cartesian-grids[J]. Journal of Computational Physics, 2010, 229(8): 2853-2865. Doi:10.1016/j.jcp.2009.12.018 |
| [34] |
Cummins S J, Francois M M, Kothe D B. Estimating curvature from volume fractions[J]. Computers & Structures, 2005, 83(6-7): 425-434. Doi:10.1016/j.compstruc.2004.08.017 |
| [35] |
Francois M M, Cummins S J, Dendy E D, et al. A balanced-force algorithm for continuous and sharp interfacial surface tension models within a volume tracking framework[J]. Journal of Computational Physics, 2006, 213(1): 141-173. Doi:10.1016/j.jcp.2005.08.004 |
| [36] |
Popinet S. Numerical models of surface tension[J]. Annual Review of Fluid Mechanics, 2018, 50: 49-75. Doi:10.1146/annurev-fluid-122316-045034 |
| [37] |
Seric I, Afkhami S, Kondic L. Direct numerical simulation of variable surface tension flows using a volume-of-fluid method[J]. Journal of Computational Physics, 2018, 352: 615-636. Doi:10.1016/j.jcp.2017.10.008 |
| [38] |
Tripathi M K, Sahu K C. Motion of an air bubble under the action of thermocapillary and buoyancy forces[J]. Computers & Fluids, 2018, 177: 58-68. Doi:10.1016/j.compfluid.2018.10.003 |
| [39] |
Johansen H, Colella P. A Cartesian grid embedded boundary method for Poisson's equation on irregular domains[J]. Journal of Computational Physics, 1998, 147(1): 60-85. Doi:10.1006/jcph.1998.5965 |
 2024, Vol. 41
2024, Vol. 41 


 ,
倪明玖1,2
,
倪明玖1,2