在研究基因型,特别是单核苷酸多态性(single nucleotide polymorphism, SNP)与表型之间的关联以及指导育种时,全基因组关联分析(genome-wide association study, GWAS)对数量性状的表型预测有着明显的作用。GWAS目前已广泛应用于许多主要农作物的育种工作中[1-3],如大豆(Glycine max)、水稻(Oryza sativa)和玉米(Zea mays)等。传统的统计方法,如最佳线性无偏预测、贝叶斯模型[4]等,目前被广泛用于预测基因型效应和预测表型。传统统计方法通常假设基因型随机效应遵循高斯分布等先验分布,同时将每个基因型对相关表型的贡献视为相互独立的因素。这些先验假设需要足够大的训练样本来修正和调整。然而,在实践中,单个基因的效应是未知的,可能不严格遵循先验分布。此外,SNPs还可与其他SNPs发生相互作用,通过上位性效应,导致复杂的疾病或性状[5]。因此,传统统计方法的准确性往往受到数据量和各种复杂遗传因素的限制。
此外,对于统计方法而言,基因型数据中的缺失值会带来巨大制约。通常,这些缺失值会在预处理过程中筛选出来,并通过插补数据进行填充[6]。插补是一种用于估计模板群体中基因型的缺失值的算法,目前已有几种具有或不具有参考基因组信息的基因组插补方法。插补精度高度依赖于观察到的非缺失基因型和整个群体的缺失率,这直接影响表型预测模型的性能[6]。通过统计方法进行表型预测的模型,需要将基因型矩阵一起估算,然后将其划分为用于模型训练和测试的训练和测试数据集。在某种程度上,测试集并非完全独立于训练集,因为在这种情况下,训练集可能包含从测试集数据中进行估计和插补产生的基因型。不准确的插补方法也可能带来误差和不确定性。因此,这些插补方法可能无法有效推断隐藏在整个基因组中的信息。
近年来,深度学习在生物学领域逐渐得到广泛的应用,在计算生物学中的一些重大挑战问题上取得了前所未有的进展。目前,深度学习已经在蛋白质结构预测、蛋白质功能预测、基因组工程、系统生物学和数据集成以及系统发育预测等5个领域得到广泛应用[7]。在部分领域,如在蛋白质功能预测方面,深度学习的性能明显超过其他机器学习模型和经典方法,并产生了广泛影响。在系统生物学和基因型关联研究中,与现有方法相比,深度学习可以整合和集成多维度的数据信息,发现具有不同数据模式特征的有意义的亚组[8],识别SNP相互作用[9]以及对基因组变异进行分类[10]。深度学习可以利用各种不同来源数据,对其进行联合建模。对于表型预测问题,神经网络可以从原始测序数据或基因型数据中直接获取信息。目前,已有多篇文献在表型预测领域中应用了深度学习,如通过癌细胞的多组学信息预测乳腺癌患者的5年生存期[8]、通过生物标志物信息预测患者的阿尔兹海默症进展[11]等,但多见于医学领域。在植物遗传学和育种方面尚未得到有效的应用,仅有少量使用神经网络预测进行辅助育种的例子[12],但很少有使用大量SNP数据的研究,且并未采用较为先进的深度学习网络。然而,上述深度学习方法同样有局限性,它们并没有有效地解决数据缺失和上位效应等问题。具体而言,深度学习可能会过度拟合数据,并且容易在训练集和测试集之间产生“污染”,这些都可能导致对性能的高估[13]。
针对传统统计分析方法和已知深度学习方法存在的问题,本文提出一个多尺度特征卷积神经网络(muti-scale feature convolutional neural network, MSF-CNN)模型,通过提取SNPs位点分布的多尺度特征预测对应植物的表型,并根据训练后模型的权重评估SNPs位点的显著性。本文利用大豆数据集分别训练株高、含水量、含油量、蛋白质含量、产量等5个表型所对应的模型,并进行模型评估。同时,分析对含油量和蛋白质含量等表型有贡献的SNPs的权重,并与Wald检验[14]的结果进行对照。结果表明,该模型与传统统计方法以及现有深度学习相比,在未插补数据集上的性状预测性能更优,在SNPs显著性分析方面也有较好的效果。
1 实验方法和材料 1.1 数据集本文以大豆作为研究对象,使用大豆的实验数据集作为基准来评估所提出模型的性能。大豆数据集来自SoyBase数据库中的SoyNAM项目,该项目是目前最完善的大豆SNP数据集[14-15]。通过对其中数据的质量控制和筛选,最终得到一个在包含5 000多个重组自交系中发现的4 236个常见SNP,以及相应的大豆株系的株高、含水量、含油量、蛋白质含量和产量等性状表型的数据集。数据集中缺失的基因型数据通过MaCH软件进行估计和补齐,与随机森林回归法和期望最大化插补法等其他插补方法相比,该插补方法误差更小、预测的准确性更高[16]。基因组选择的效果依赖于基因标记的覆盖率,因此为了以低成本获得大量基因标记,通常会使用较低的测序深度,难免产生大量位点缺失的数据,而大多数分析需要完整的数据。因此,在将测序基因分型的数据用于分析之前,插补往往是必要的步骤。研究表明,对缺失数据的插补可以提高遗传关联研究的能力[6]。而在深度学习网络的训练中,使用一个独立的编码代表数据缺失,因此可以使用未经插补的原始数据直接进行训练,而不需经过插补。我们在训练模型时,使用经插补的数据和未经插补的数据分别进行训练,并比较了两者的训练效果。
1.1.1 SNP表示本文对性状数据进行了规整化以便训练,将其均转换为(-1,1)区间内的数值。模型中,输入的性状数据为一个列表,其内容包含植株个体的编号、每一个个体在4 236个常见SNP位点的基因型,及其性状数据。SNP按其所在染色体及染色体上的位置按顺序进行排序,依次由1号染色体列至20号染色体。每一个SNP可被视为输入矩阵中独立的一行,因此SNP的顺序不影响训练的结果。对于每一个性状,输入的SNP数据均相同。使用多个二进制编码构成的向量代表一个SNP位点的3种基因型(0、1、2)以及数据缺失(-1),并以此作为输入向量的一部分。每一种基因型由一个对应位置为1的4维向量表示,其余的设置为0。例如,3种基因型[AA,Aa,aa]分别表示为[0, 1, 0, 0],[0, 0, 0, 1]和[0, 0, 1, 0]。缺失的基因型表示为[1, 0, 0, 0]。由于SNP数据已通过对基因组序列的预处理进行了提炼,SNP数据本身并不包含基因序列信息,仅为区分3种不同基因型[AA,Aa,aa]的标记,因此不会受基因序列的同源性影响,避免了训练集、验证集、测试集之间的样本交叉。
1.1.2 性状数据标准化对表型数据进行标准化,将其转化为z分数。其公式如下
| $\begin{equation*} Z=\frac{x-\bar{x}}{s} . \end{equation*} $ | (1) |
其中:Z表示转换后的z分数;x代表性状数据;代表该性状数据的平均值;s代表该性状数据的标准差。通过表型数据的标准化,可以提取性状数据的差异特征,更有利于模型的训练。
1.2 MSF-CNN 1.2.1 模型结构密集卷积网络(dense convolutional network, DenseNet)是一种较新的网络结构[17]。其特征为其每一层都与其他层相连。每一层使用所有先前层的特征图作为输入,其自身的特征图作为所有后续层的输入。因为卷积网络在靠近输入的层和靠近输出的层之间包含较短的连接,因此卷积网络可以更深入、更准确、更有效地训练。
本文借鉴DenseNet结构的特点,构建MSF-CNN,其结构如图 1所示。模型包括1个输入层、4个卷积层、2个拼接层、1个平坦层、1个全连接层和1个输出。输入数据向量包含4 236个SNP;每个SNP位点对应1个如2.1.1节所述的4维向量,因此输入层所输入的数据为1个4 236×4的矩阵。在经过第1个卷积层的处理后,转变为4 236×12的矩阵。随后,在卷积层后又加入池化层,得到大小为2 118×12的矩阵。以上2个矩阵通过接合层进行接合,最终在第1个拼接层产生1个6 354×12的矩阵。同理,当这一矩阵再次进行后续的卷积、池化、拼接过程后,在第2个拼接层生成1个9 531×12的矩阵。该矩阵由多层次之间的数据接合形成,因此具备多尺度下的数据特征,可以比过往模型更有效地挖掘和预测数据之间存在的多尺度关联与相互作用。在2次拼接之后,数据再次通过一次卷积进行后处理,并输出到平坦层。平坦层将特征矩阵展开为1维向量并传递到最后一个全连接层,输出最终预测的表型。
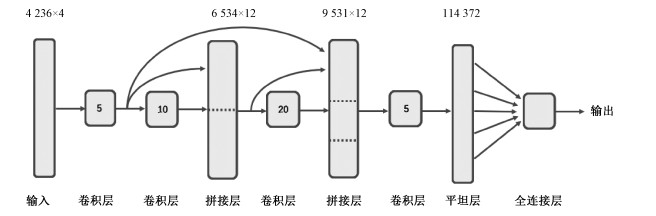
|
Download:
|
| 图 1 神经网络结构 Fig. 1 Neural network structure | |
本文在模型中使用双曲正切函数作为全连接层回归预测激活函数,其定义如下所示
| $\begin{equation*} y=b \tanh (x)=b \frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} . \end{equation*} $ | (2) |
其中: b为一个固定的参数,x和y分别代表处理前后的性状数据。
我们尝试了几种激活函数,包括平方根倒数、Sigmoid函数和双曲正切函数。在测试中发现双曲正切函数的效果最好,在训练中损失函数的收敛最快,因此选择双曲正切函数作为激活函数。双曲正切函数可以增强对表型预测值的约束,并加快模型学习过程,因为双曲正切函数可以在数据处理中引入非线性因素,使得依赖于线性变换的神经网络可以逼近非线性的函数,更适用于非线性的模型和数据。激活函数的值被限制在(-b, b)。其中,b的值由不同性状的数值范围而定,在本文的实验中,高度、含水量、含油量、蛋白质含量和产量使用的b分别为6.4、5.4、6.4、6.4和1.5。
1.2.3 损失函数本文使用实测表型和预测表型之间的均方误差(mean-square error, MSE)作为损失函数,其定义如下所示
| $ \begin{equation*} \text { MSE }=\frac{1}{n} \sum _{i=1}^{n}\left(\widetilde{Y_{i}}-Y_{i}\right)^{2} . \end{equation*} $ | (3) |
式中:
通过监测验证集上的MSE,并在观察到验证集的MSE满足停止条件时停止模型训练过程,从而防止模型在达到极限时继续训练形成过拟合。
1.2.4 模型性能分析通过皮尔逊相关系数(pearson correlation coefficient, PCC)比较预测值与实测性状数值之间的相关性,以反映和比较不同模型的预测性能。PCC用于度量2个变量X和Y之间的相关性,PCC值在-1~1之间,愈大表示2个变量的相近程度愈高。PCC计算方法如下所示
| $ \begin{equation*} r=\frac{\sum\limits_{i=1}^{n}\left(X_{i}-\bar{X}\right)\left(Y_{i}-\bar{Y}\right)}{\sqrt{\sum\limits_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}} \sqrt{\sum\limits_{i=1}^{n}\left(Y_{i}-\bar{Y}\right)^{2}}} . \end{equation*} $ | (4) |
式中: Xi和Yi分别代表 2个变量的值,而和代表 2个变量的平均值。在生物分析中,常用标签量与预测量之间的PCC评估预测模型的性能[18]。
1.2.5 SNP显著性分析Simonyan和Zisserman[19]提出一种基于模型中的权重可视化显著性的方法,通过以下公式可以提取模型中各输入变量的权重:
| $\begin{equation*} S_{c}(I)=\boldsymbol{\omega}_{c}^{\mathrm{T}} \boldsymbol{I}+b_{c} . \end{equation*} $ | (5) |
式中:S代表显著性值,I代表SNP数据所转化为的向量,ω和b分别代表相应的权重向量和模型误差。为评估利用MSF-CNN模型进行SNPs显著性分析的效果,本文提取与显著性相对应的各输入SNP的权重,并与经验贝叶斯模型的Wald统计检验值进行对比。
1.2.6 过拟合控制当数据集的训练样本量很小,而总样本量远小于用作特征的基因型数量以及模型中参数数量时,就会出现过拟合现象。Srivastava等[20]提出采用丢弃层降低过拟合的方法。丢弃层在每次迭代的训练过程中从神经网络中随机丢弃部分节点以及它们之间的连接。丢弃不同节点,相当于训练不同的神经网络。丢弃过程类似于对大量不同网络的影响进行平均,减少过拟合。为减少过拟合的影响,在每个卷积层之后添加了丢弃层。
2 结果与讨论 2.1 模型训练本文模型在Tensorflow平台上实现,并在具有NVidia GTX 1070 Ti GPU的工作站上完成训练。
在训练时,将数据集随机分为10个样本数相同的组,以其中8组作为训练集,另外2组分别为验证集和测试集。训练集、验证集和测试集彼此无相同样本。训练过程中选择每轮样本批量为250,训练轮数为1 000。
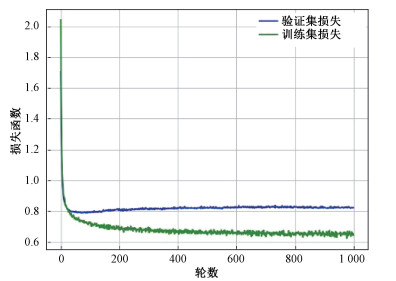
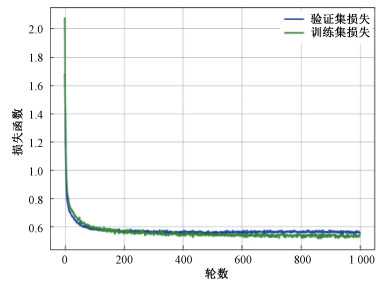
训练过程中训练集损失函数和验证集损失函数的变化曲线如图 2、图 3所示。其中,图 2是以使用算法[16]预测缺失值并进行插补的数据集进行训练的结果;图 3是使用未经处理和插补的原始数据集的训练曲线。图 2和图 3表明,损失函数随迭代次数增加而逐渐减少,在迭代次数小于100次的训练初期大幅降低,而在迭代次数大于100次时,损失函数变化很小,逐渐趋近于平稳。2个数据集训练后模型的性能有较大的差异。对于进行插补后的数据集,损失函数在100次迭代后略有升高,出现过拟合的现象。这可能是由于样本量有限,插补的数据同样由原始数据推测得到,在训练中更容易发生过拟合。
|
Download:
|
| 图 2 以插补后的数据集训练的损失函数图 Fig. 2 Loss functions of the data set with data imputation | |
|
Download:
|
| 图 3 以未经插补的数据集训练的损失函数图 Fig. 3 Loss functions of the data set without data imputation | |
为提高训练速度,在实际训练过程中自动检测验证集上的损失, 当7次迭代后验证集损失函数值不再降低时,自动停止训练。
2.2 多种模型的性状预测性能比较利用训练得到的模型开展性状预测。模型输入SNP向量数据,输出所预测的性状数值。
为评估MSF-CNN深度学习模型的性能,计算测试数据集的基因组预测表型和观察(标签)表型值之间的PCC,并与使用相同训练、验证和测试数据集的已知主要分析模型进行比较。本文选择文献中性能最好的单层卷积神经网络(singleCNN)和双层卷积神经网络(DualCNN)深度学习模型,以及rrBLUP、BRR、贝叶斯模统计分析模型等[21]作为比较对象。
选择用10种训练集、测试集和验证集分组,分别进行10次模型训练,评估每次训练后模型的PCC,计算10次训练模型的平均值,并将结果与所选算法和模型的结果进行对照。表 1列出MSF-CNN模型与比较对象的PCC。
|
|
表 1 MSF-CNN与现有卷积神经网络模型进行不同表型预测时的PCC值[20] Table 1 PCC value between MSF-CNN and existing convolution neural network models for phenotype prediction[20] |
由表 1可见,当使用插补后的数据进行训练时,本文模型与现有的神经网络模型效果相当。而当使用原始数据进行训练时,基于MSF-CNN的模型效果均优于现有模型。与现有的传统统计学方法以及卷积神经网络模型相比,MSF-CNN模型性能有所提高,且大幅优于传统统计学方法。卷积神经网络的对应训练结果数据来自于文献[21]。
在表 1中,MSF-CNN模型在估算未经插补的原始数据时PCC均高于经插补的数据。这一结果表明,MSF-CNN模型在进行表型预测和SNP分析时可以部分克服数据缺失造成的影响,直接输入原始数据进行分析,而无需像传统的基因组关联分析一样进行插补预处理。因此,通过MSF-CNN模型进行表型预测更加便捷,且不易受插补过程中产生的误差的影响。大豆数据集的原始数据集中缺失约25% 的基因型信息,MSF-CNN模型在原始数据集上具有更高预测性能的一个原因可能是,插补过程用原始数据中等位基因信息作为参考,填充了大多数缺失的基因型,因此缩小了数据中不同基因型的影响。
MSF-CNN模型在含油量和株高这2个高遗传性的性状上具有更优秀的表现,与其他模型相比,优势更明显。这可能是因为MSF-CNN融合了更多尺度的特征信息,从而有助于发现基因之间的多层次关联。
2.3 SNP显著性分析虽然深度学习模型可解释性较差,但通过获取模型中各个输入变量的权重,可以分析各输入变量对预测结果影响的显著性。输入变量权重的大小表示该变量对预测结果影响的显著性程度。
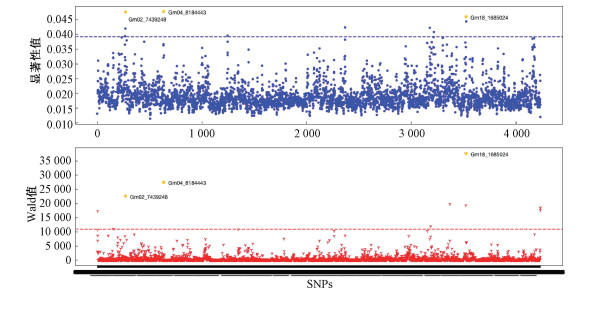
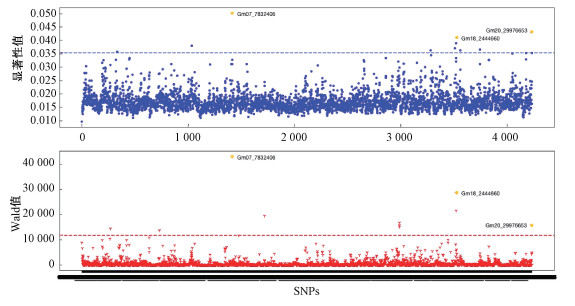
使用曼哈顿图画出MSF-CNN模型输入SNPs的权重分布图和Wald检验值分布图,将MSF-CNN模型的各SNP的权重(显著性值)与贝叶斯模型Wald值直接对照,可标记出MSF-CNN模型中权重较大(通过显著性图分析)的部分重要SNP及其在Wald检验结果图中的相应位置。
图 4和图 5分别是使用本文大豆数据集所训练的含油量和蛋白质含量预测模型的显著性分析对照图。图中将在显著性分析中排名靠前(权重大)的SNP用红色标出。部分在MSF-CNN模型中显著性突出的SNP位点在Wald检验中同样重要。由图中可见,2种分析方法中有部分显著位点重叠,但同时也有部分位点仅在一种分析方法中突出。对于大豆的含油量和蛋白质含量,位点的重合度较高;而对于株高、含水量和产量则重合度相对较低。由于缺乏对应位点的实验研究检验基因功能,难以判断2种方法的准确性。经2种分析方法检验的重叠位点有更大概率可能与该性状有关。显著性分析的准确性难以验证使其在深度学习网络应用中仍存在一定的局限性。
|
Download:
|
| 图 4 各SNP对大豆含油量性状的贡献显著性 Fig. 4 Comparison of the contribution of each SNP to oil content trait | |
|
Download:
|
| 图 5 各SNP对大豆蛋白质含量性状的贡献显著性 Fig. 5 Comparison of the contribution of each SNP to protein content trait | |
在以已识别SNP为中心的20 kbp区域内找到了最近的基因,并标注了其名称和功能。根据基因模型“Glyma.Wm82.a1.v.1”[22],使用Soybase数据库[23]和SoyKB [24]的蛋白质家族(PFAM)数据库[25]进行注释。基因注释表明,图中标注的SNP位点及其附近区域与它们的性状高度相关。另外,也检测到几个新的标记和区域。
通过对大豆产量预测模型的显著性分析,发现Gm02_6396340、Gm03_5730188、Gm03_5816390、Gm04_2571383等几个SNP在模型中对性状的影响最为显著。考察与这些SNP位点距离最接近的基因,发现Gm02_6396340的位点与大豆基因Glyma.02g073100重叠,该基因编码一个包含成簇蛋白结合域的高GC区DNA结合蛋白(PF07842);Gm03_5730188的位点接近基因Glyma.03g045300,其编码一个包含NB-ARC区域的蛋白(PF00931);Gm03_5816390的位点与基因Glyma.03g045700重叠,其编码一个包含NB-ARC区域以及LRR的蛋白(PF00560);Gm04_2571383的位点接近基因Glyma.04g032000,其编码一个亮氨酸羧基甲基转移酶家族的蛋白(PF04072)。
通过对大豆株高预测模型的显著性分析,发现Gm10_44287415、Gm10_44500915、Gm10_ 44669893、Gm11_1266080等几个SNP在模型中对性状的影响最为显著。位于大豆10号染色体上的一个区域含有多个显著位点。考察与该SNP位点距离最接近的基因,发现Gm10_44287415的位点与基因Glyma.10g210600重叠,其编码一个生长素响应因子(PF06507);Gm10_44500915的位点与基因Glyma.10g212500重叠,其编码一个丝氨酸羧肽酶家族蛋白(PF00450);Gm10_ 44669893接近基因S58482.1,其表达被生长素下调;Gm11_1266080的位点接近基因AP2-9,其编码一个AP2-EREBP转录因子,AP2家族基因据报道可调节大豆的生长素合成,当其过表达时会提高大豆株高[26]。
通过对大豆含水量预测模型的显著性分析,发现Gm10_44124696、Gm10_44287415、Gm15_9530676、Gm17_6781998等几个SNP在模型中对性状的影响最为显著。考察与该SNP位点距离最接近的基因,其中Gm10_44124696接近基因Glyma.10g209200,其编码一个ATP结合盒转运蛋白(PF00005);Gm10_44287415已在株高一节中提及;Gm15_9530676接近基因Glyma.15g120300,其编码一个姐妹染色单体凝聚蛋白;最接近Gm17_6781998位点的基因Glyma17g09165属于蛋白激酶结构域(PF00069),并参与对寒冷、创伤、盐胁迫和甘露醇刺激等反应的生物学过程。
通过对大豆蛋白质含量预测模型的显著性分析,发现Gm07_7832406、Gm18_2444660、Gm20_29976653等几个SNP在模型中对性状的影响最为显著。同时,它们在Wald检验中同样显示有较强的显著性。考察与上述SNP位点距离最接近的基因,其中Gm07_7832406位点与基因Glyma.07g085000重叠,其编码一个植物特异性的Rop蛋白(PF03759);Gm18_2444660位点接近基因Glyma.18g031700;Gm20_29976653位点接近基因Glyma.20g080300,其编码一个磷酸酶家族蛋白(PF03372)。
通过对大豆含油量预测模型的显著性分析,发现Gm02_7439248、Gm04_8184443、Gm18_1685024等几个SNP在模型中对性状的影响最为显著。同时,它们在Wald检验中也显示有较强的显著性。Gm02_7439248位点与基因Glyma.02g085400重叠,其编码一个起RNA代谢功能的金属β-内酰胺酶(PF07521);Gm04_8184443与基因Glyma04g09900接近,该基因属于蛋白酪氨酸激酶家族(PF07714),涉及蛋白磷酸化过程和寡肽转运过程;Gm18_1685024位点接近基因Glyma.18g023100,其编码一个预苯酸脱氢酶(PF02153)。
3 结论本文提出一种基于密集卷积网络的深度学习模型MSF-CNN,可以通过SNP标记准确预测表型,而不需要对原始数据中缺失的基因型进行插补。探索几种不同的深度学习架构,并对原本的密集卷积网络模型进行简化和优化,最终得到优化的模型结构。与目前常用的神经网络模型相比,该模型在真实实验数据集上具有最佳的预测性能。通过显著性图研究不同位点和基因对性状的贡献,发现了数个较显著的SNP位点。该模型还需要继续改进,使其具备明确所研究基因型间的相互作用对表型的影响、解释预测结果的潜在生物学意义的能力,为表型预测和SNP选择发挥作用。
| [1] |
Zhao Y S, Gowda M, Liu W X, et al. Accuracy of genomic selection in European maize elite breeding populations[J]. Theoretical and Applied Genetics, 2012, 124(4): 769-776. Doi:10.1007/s00122-011-1745-y |
| [2] |
Spindel J, Begum H, Akdemir D, et al. Genomic selection and association mapping in rice (Oryza sativa): effect of trait genetic architecture, training population composition, marker number and statistical model on accuracy of rice genomic selection in elite, tropical rice breeding lines[J]. PLoS Genetics, 2015, 11(2): e1004982. Doi:10.1371/journal.pgen.1004982 |
| [3] |
Xavier A, Jarquin D, Howard R, et al. Genome-wide analysis of grain yield stability and environmental interactions in a multiparental soybean population[J]. G3-Genes Genomes Genetics, 2018, 8(2): 519-529. Doi:10.1534/g3.117.300300 |
| [4] |
Endelman J B. Ridge regression and other kernels for genomic selection with R package rrBLUP[J]. The Plant Genome, 2011, 4(3): 250-255. Doi:10.3835/plantgenome2011.08.0024 |
| [5] |
Wang J X, Joshi T, Valliyodan B, et al. A Bayesian model for detection of high-order interactions among genetic variants in genome-wide association studies[J]. BMC Genomics, 2015, 16: 1011. Doi:10.1186/s12864-015-2217-6 |
| [6] |
Rutkoski J E, Poland J, Jannink J L, et al. Imputation of unordered markers and the impact on genomic selection accuracy[J]. G3 Genes|Genomes|Genetics, 2013, 3(3): 427-439. Doi:10.1534/g3.112.005363 |
| [7] |
Sapoval N, Aghazadeh A, Nute M G, et al. Current progress and open challenges for applying deep learning across the biosciences[J]. Nature Communications, 2022, 13(1): 1-12. Doi:10.1038/s41467-022-29268-7 |
| [8] |
Tong L, Mitchel J, Chatlin K, et al. Deep learning based feature-level integration of multi-omics data for breast cancer patients survival analysis[J]. BMC Medical Informatics and Decision Making, 2020, 20(1): 225. Doi:10.1186/s12911-020-01225-8 |
| [9] |
Uppu S, Krishna A, Gopalan R P. A deep learning approach to detect SNP interactions[J]. Journal of Software, 2016, 11(10): 965-975. Doi:10.17706/jsw.11.10.965-975 |
| [10] |
Liang Z H, Huang J X, Zeng X, et al. DL-ADR: a novel deep learning model for classifying genomic variants into adverse drug reactions[J]. BMC Medical Genomics, 2016, 9(S2): 48. Doi:10.1186/s12920-016-0207-4 |
| [11] |
Lee G, Nho K, Kang B, et al. Predicting Alzheimer's disease progression using multi-modal deep learning approach[J]. Scientific Reports, 2019, 9(1): 1-12. Doi:10.1038/s41598-018-37769-z |
| [12] |
Zingaretti L M, Gezan S A, Ferrão L F V, et al. Exploring deep learning for complex trait genomic prediction in polyploid outcrossing species[J]. Frontiers in Plant Science, 2020, 11: 25. Doi:10.3389/fpls.2020.00025 |
| [13] |
Whalen S, Schreiber J, Noble W S, et al. Navigating the pitfalls of applying machine learning in genomics[J]. Nature Reviews Genetics, 2022, 23(3): 169-181. Doi:10.1038/s41576-021-00434-9 |
| [14] |
Xavier A, Beavis W D, Specht J E, et al. SoyNAM: soybean nested association mapping dataset[DB]. R package version, 2015, 1.
|
| [15] |
Song Q J, Yan L, Quigley C, et al. Genetic characterization of the soybean nested association mapping population[J]. The Plant Genome, 2017, 10(2): 10. Doi:10.3835/plantgenome2016.10.0109 |
| [16] |
Li Y, Willer C J, Ding J, et al. MaCH: using sequence and genotype data to estimate haplotypes and unobserved genotypes[J]. Genetic Epidemiology, 2010, 34(8): 816-834. Doi:10.1002/gepi.20533 |
| [17] |
Huang G, Liu Z, Van Der Maaten L, et al. Densely connected convolutional networks[C]. 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). July 21-26, 2017, Honolulu, HI, USA. IEEE, 2017: 2261-2269. DOI: 10.1109/CVPR.2017.243.
|
| [18] |
Zhang X Z, Wang Y F, Shi W S. pCAMP: performance comparison of machine learning packages on the edges[EB/OL]. (2019-06-05)[2023-03-24]. https://arxiv.org/abs/1906.01878.
|
| [19] |
Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition[EB/OL]. (2014-09-04)[2023-03-24]. https://arxiv.org/abs/1409.1556.
|
| [20] |
Srivastava N, Hinton G, Krizhevsky A, et al. Dropout: a simple way to prevent neural networks from overfitting[J]. The Journal of Machine Learning Research, 2014, 15(1): 1929-1958. |
| [21] |
Liu Y, Wang D L, He F, et al. Phenotype prediction and genome-wide association study using deep convolutional neural network of soybean[J]. Frontiers in Genetics, 2019, 10: 1091. Doi:10.3389/fgene.2019.01091 |
| [22] |
Schmutz J, Cannon S B, Schlueter J, et al. Erratum: genome sequence of the palaeopolyploid soybean[J]. Nature, 2010, 465(7294): 120. Doi:10.1038/nature08957 |
| [23] |
Grant D, Nelson R T, Cannon S B, et al. SoyBase, the USDA-ARS soybean genetics and genomics database[J]. Nucleic Acids Research, 2010, 38(Suppl 1): D843-D846. Doi:10.1093/nar/gkp798 |
| [24] |
Joshi T, Patil K, Fitzpatrick M R, et al. Soybean knowledge base (SoyKB): a web resource for soybean translational genomics[J]. BMC Genomics, 2012, 13(Suppl 1): S15. Doi:10.1186/1471-2164-13-S1-S15 |
| [25] |
Bateman A, Coin L, Durbin R, et al. The Pfam protein families database[J]. Nucleic Acids Research, 2004, 32(Suppl 1): D138-D141. Doi:10.1093/nar/gkh121 |
| [26] |
Xu Z Y, Wang R K, Kong K K, et al. An APETALA2/ethylene responsive factor transcription factor GmCRF4a regulates plant height and auxin biosynthesis in soybean[J]. Frontiers in Plant Science, 2022, 13: 983650. Doi:10.3389/fpls.2022.983650 |
 2024, Vol. 41
2024, Vol. 41 


