2. 中国科学院大学,北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
全球大气CO2的质量分数从2000年的368.0×10-6迅速增加到2020年的412.4×10-6,主要由化石燃料燃烧产生的碳排放引起,其中中国的占比最大(31%)[1-2]。2018年,中国CO2排放量为9 570.8 Mt,其中燃煤电厂CO2排放量为4 747.9 Mt,占比超过49%。2019—2021年期间,中国燃煤电厂新增电力3.3×1010 kW·h,增长近7%[3]。因此,准确估算中国燃煤电厂CO2排放量有助于人为碳排放监测以及针对性制定碳排放政策。
目前,估算电厂CO2排放量的方法主要有2种: 1)基于燃料燃烧数据和排放因子的自下而上模型;2)基于实测单个电厂气体浓度或流速的自上而下模型。自下而上的排放清单受统计数据约束,排放因子随着特定地区和电厂参数而变化,并且相关的机组信息可能不公开,导致时间分辨率从小时到年不等。特别是欠发达地区缺乏电厂排放信息[4-6]。近年来,遥感观测数据结合自上而下大气模型为估算电厂CO2排放提供了一种新的方法。该方法基于实测卫星数据, 较少受到人为因素影响并且时间分辨率较高,为不同地区的估算提供了统一的标准[7]。
一些学者利用航空或地面遥感观测获取特定电厂的CO2信息。Ahn等[8]和Whetstone[9]使用机载仪器测量城市和发电厂地区的CO2摩尔分数。Krings等[10-11]利用航空光谱仪对电厂区域的柱平均CO2浓度(XCO2)进行遥感测量,但这种方法成本高且无法进行长时间连续监测。Hirofumi等[12]和Zhou等[13]使用便携式傅里叶红外光谱仪实现特定电厂和城市地区的地面CO2柱浓度测量,但无法实现大面积同步观测。
卫星遥感可以实现大面积、长时间序列XCO2测量。其中,轨道碳观测者2号(Orbiting Carbon Observatory 2, OCO-2)因其约3 km2的高空间分辨率和1×10-6的测量精度广泛应用于科学研究[14]。许多学者结合OCO-2数据和拉格朗日粒子扩散模型(stochastic time-inverted Lagrangian transport, X-STILT)、天气研究和预测-化学模型(the weather research and forecasting model coupled with chemistry, WRF-Chem)以及通量截面法等估算城市和工业区的CO2排放量[7, 15-16]。Nassar等[17-18]利用OCO-2和高斯羽流模型在空间尺度上估算了单个电厂的CO2排放量。Hu和Shi[19]发现克里金插值可以增加高斯羽流模型模拟所需的有效XCO2数据。Zheng等[20]提出一种将OCO-2与WRF-Chem模型相结合的新方法,但在电厂水平上没有显示出比高斯羽流模型更高的精度。这些研究都显示了OCO-2卫星数据结合大气模型量化碳排放的优势,但由于OCO-2成像宽度窄(~10 km),重访周期长(16 d),且易受云层影响,地球上很多地方无法获得数据[21]。因此仅利用OCO-2卫星数据很难在发电厂等小规模地区识别足够有效的XCO2观测数据。
轨道碳观测者3号(Orbiting Carbon Observatory 3, OCO-3)于2019年5月4日发射进入国际空间站(International Space Station, ISS)轨道。由于使用了指向镜组件(pointing mirror assembly, PMA),OCO-3新增快照区域地图(snapshot area map, SAM)模式。在该模式中,OCO-3收集几乎相邻的数据带,扩展了对发电站和火山等排放热点的观测能力[22]。Kiel等[23]使用OCO-3 vEarly XCO2数据确定了洛杉矶市内(0~6)×10-6的XCO2增强。Zhou等[13]利用OCO-2/3卫星XCO2数据验证傅里叶红外光谱仪测量的CO2柱浓度数据,结果显示相关性为0.88~0.96。Macdonald等[24]利用OCO-2/3观测数据计算全球27个大城市的XCO2增强。因此整合同一点源的多源卫星成像可以提高电厂识别和估算CO2排放的效率和精度。
本研究旨在利用OCO-2/3卫星和高斯羽流模型估算中国燃煤电厂的CO2排放量。首先,筛选中国区域内超大型电厂附近的卫星成像情况,并识别可用的CO2羽流。然后利用不同背景值确定方法获得高精度XCO2观测增强,通过高斯羽流模型估算电厂CO2排放量并考虑羽流上升。最后,将估算结果与其他排放清单进行比较以验证本研究估算结果的准确性。本研究使用卫星遥感反演方法,避免了统计数据时效性低和排放因子不准确造成的误差,可为排放清单的更新优化和针对性制定碳减排政策提供数据支撑。
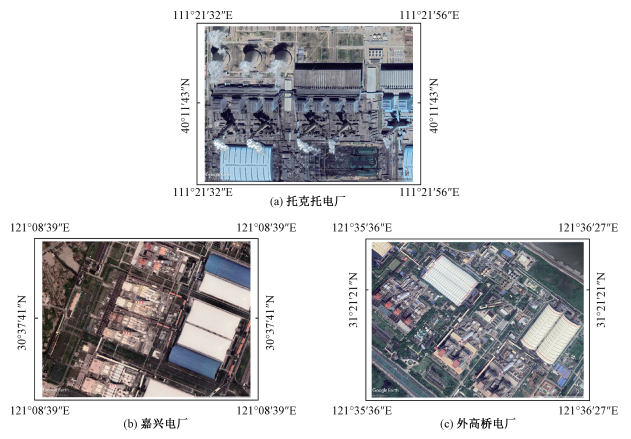
1 研究区本文研究区域包括3个超大型电厂(图 1)。
|
Download:
|
| 图 1 电厂位置示意图 Fig. 1 Schematic diagram of power plant location | |
托克托电厂位于内蒙古自治区呼和浩特市托克托县,是国家重点建设项目,也是国家“西部大开发”和“西电东送”的重点工程[25]。电厂共分5期完成,前4期工程于2011年完成,共有8×600 MW和2×300 MW(自备)机组投产发电,5期2×660 MW于2017年投产,总装机容量6 720 MW,是全球装机容量最大的燃煤电厂。
1.2 外高桥电厂外高桥电厂位于上海市浦东新区北部,总装机容量5 000 MW,占上海市总装机容量的25%。电厂分3期完成:1期工程由4台300 MW的国产亚临界机组组成;2期工程由2台900 MW的进口超临界机组组成;3期工程由2台2 000 MW的进口超超临界机组组成。其超超临界机组能耗仅是中国平均火电厂能耗的82%,分别于1993、2004和2008年投产发电[26]。
1.3 嘉兴电厂嘉兴电厂位于浙江省平湖市,地处长江三角洲经济发达地区。1期工程于1995年投产发电,由2个装机容量为300 MW的机组组成,2013年改为330 MW;2期工程包括4台机组,相继于2004、2005年投产发电,各机组装机容量为600 MW,总装机容量2 400 MW;3期工程包括2台装机容量为1 000 MW机组,于2011年投产发电。至今嘉兴电厂总装机容量5 060 MW,为世界10大燃煤电厂之一。3期工程烟囱的几何高度均为240 m,全厂等效单源高度507 m[27]。
2 数据和方法 2.1 源数据1) 卫星数据
OCO-2是美国宇航局于2014-07-02成功发射的致力于大气CO2研究的遥感卫星。它运行在太阳同步轨道(约705 km)上,大约在13:36过境升交点。在1.61和2.06 μm短波红外波段测量CO2,同时在0.76 μm近红外波段测量O2,然后反演得到CO2柱浓度(XCO2)[21, 28]。OCO-3作为外部有效载荷安装在国际空间站的日本实验模块暴露设施上,OCO-3中使用的光谱仪与OCO-2相同,因此,OCO-3也同时测量O2带和强、弱CO2带以提供XCO2。它在3 Hz下测量精度同样优于1×10-6,每次测量包含8个足迹点,大小约为1.6 km×2.2 km[29]。因为国际空间站每天绕地球运行15.5圈,因此很难预测OCO-3的每日采样时间和观测位置。同时该轨道允许OCO-3从大约52°以下的纬度观察地球,因此OCO-3观测位置集中在人类活动强烈的中纬度地区[22]。本研究使用OCO-2 L2 Lite FP v10和OCO-3 L2 Lite FP v10, 这些数据通过戈达德地球科学数据和信息服务中心(Goddard Earth Sciences Data and Information Services Center, GES DISC)以netCDF4格式公开分发和存档。
2) 气象数据
气象数据对于模拟大气成分的运动和扩散轨迹至关重要[30]。本研究使用2种气象再分析数据,以减少估算偶然性:第5代欧洲中期天气预报中心全球气候大气再分析数据集(the fifth generation ECMWF atmospheric reanalysis of the global climate, ERA5)[31]和现代研究和应用回顾性分析第2版(modern-era retrospective analysis for research and applications, version 2, MERRA-2)[32]。在本研究中,羽流中线风由ERA5(0.25°×0.25°,1 h,37 levels)和MERRA-2(0.625°×0.5°,3 h,42 levels)中的U和V风矢量确定,并插值到卫星探测时间和烟囱高度(如果没有公共信息支持,烟囱高度默认为240 m)。近地面风速数据采用ERA5-Land每小时数据中的10 m U和V数据,空间分辨率进一步提高到0.1°×0.1°,可以更准确地表示近地面风速信息。
3) 电厂数据
本研究从全球电厂数据库(global power plant database, GPPD)和全球能源监测(global energy monitor, GEM)2个数据集获取中国燃煤电厂信息。GPPD是一个全面的开源数据库,它记录了全球发电厂的地理位置和装机容量,但GEM拥有更加丰富、准确的电厂机组信息。最后,通过谷歌地图进行精准的目视确认以保证地理位置的准确性。此外,全球发展中心的碳监测行动(carbon monitoring for action, CARMA)数据库[33]、全球电力排放数据库(global power emissions database, GPED)[5]以及Carbon Brief网站上发布的全球燃煤电厂地图(https://www.carbonbrief.org/mapped-worlds-coal-power-plants/)均记录了发电厂的CO2排放量信息,同样用于高斯羽流模型估算结果的验证。
2.2 高斯羽流模型高斯羽流模型被广泛用于模拟点源排放物的运动和扩散特性[34]。电厂烟囱CO2排放在一定条件下近似符合连续正态分布特征。模型公式如下
| $ \Delta V(x, y)=\frac{F}{\sqrt{2 {\mathsf{π}}} \sigma_{y}(x) \mu} \mathrm{e}^{-\frac{1}{2}\left(\frac{y}{\sigma_{y}(x)}\right)^{2}}, $ | (1) |
| $ \sigma_{y}(x)=a \cdot\left(\frac{x}{x_{0}}\right)^{0.894}. $ | (2) |
式中:“ΔV(x, y)”表示在(x, y)坐标处的垂直柱浓度(g/m2);(x, y)表示沿风向的距离(m)和垂直风向距离(m);μ表示羽流中线处的风速(m/s);F为电厂瞬时CO2排放速率(g/s);σy(x)为y方向上的标准差,反映CO2垂直扩散率;x0是特征长度,为1 000 m;a为大气稳定性参数。因为OCO-2/3对云和气溶胶敏感,不在黑暗或者多云的情况下成像,因此本研究根据改进的Pasquell-Gifford稳定性分类法由卫星经过时的日射强度,地面10 m风速确定a值[17]。
最后,对观测到的XCO2增强量和模拟的单位排放XCO2增强量(y为观测增强量,x为模拟增强量)进行线性最小二乘拟合,得到目标电厂CO2排放通量。模拟增强由高斯羽流模型公式给出,观测到的XCO2增强由卫星观测到的XCO2减去大气背景XCO2浓度得到。本研究不仅将不同区域观测值的中值或平均值作为电厂附近XCO2的大气背景值,还增加了另外2种不同的背景值确定方法,即两步线性回归法[15]、拟合高斯曲线法[16],公式如下
1) 两步线性回归法
| $ \mathrm{XCO}_{2}=\mathrm{XCO}_{2_{\text {trend}}}+\mathrm{XCO}_{2_{\text {local}}}, $ | (3) |
| $ \mathrm{XCO}_{2_{\text {background}}}<\mathrm{XCO}_{2_{\text {trend}}}+0.5 \delta_{\text {local}} . $ | (4) |
式中:XCO2trend为第1次线性拟合的趋势,“XCO2trend=ax+b”,x是沿轨迹的距离;XCO2local是一种局部增强;δlocal是标准差;利用该公式过滤小于“XCO2trend+0.5δlocal”的足迹点作为背景点,对背景线进行第2次线性拟合。
2) 拟合高斯曲线法
| $ y=m \cdot x+b+\frac{A}{\sigma \sqrt{2 {\mathsf{π}}}} \mathrm{e}^{\left[-\frac{(X-\mu)^{2}}{2 \sigma^{2}}\right]} $ | (5) |
式中:y为卫星观测XCO2(×10-6);x是沿轨道的距离(km);m, b, A,μ和σ为曲线的形状参数,通过非线性最小二乘拟合得到。
高斯羽流模型模拟的CO2垂直柱质量浓度为g/m2,卫星观测数据为1×10-6。因此计算得到的模拟值用Zheng等[16]提出的方法使其单位和观测值一致
| $ \mathrm{XCO}_{2}=V(x, y) \cdot \frac{M_{\text {air}}}{M_{\mathrm{CO}_{2}}} \cdot \frac{g}{P_{\text {surf}}-w \cdot \mathrm{g}} \cdot 1\;000. $ | (6) |
式中:Mair、MCO2和g为常数,分别表示空气和CO2的摩尔分子质量(kg/mol)和重力加速度(m/s2);Psurf和w表示表面压力(hpa)和气柱的总水蒸气含量(kg/m2)。
2.3 不确定性分析方法本研究采用高斯羽流模型估算电厂排放的不确定性主要来自以下几个方面
| $ \varepsilon=\sqrt{\varepsilon_{\mathrm{w}}^{2}+\varepsilon_{\mathrm{b}}^{2}+\varepsilon_{\mathrm{e}}^{2}+\varepsilon_{\mathrm{s}}^{2}+\varepsilon_{\mathrm{r}}^{2}}. $ | (7) |
式中:εw2代表风的不确定性,2个气象数据差异决定了它的大小;εb2代表背景值的不确定度,由背景值集合的标准差决定;εe2为观测增强值的不确定度,来自卫星数据文件中的XCO2uncertainty;εs2为二次源不确定度,它取决于目标电厂附近是否有其他高强度工业源;εr2表示羽流上升的不确定度。杨文燕等[35]研究表明CO2浓度会随大气层高度变化,因此本研究查询各电厂烟囱的等效单源高度。如果不确定,本研究认为电厂烟囱高度为240 m,羽流上升为250 m[36],取上下共6个不同高度排放量的标准差来表示羽流上升的不确定性。
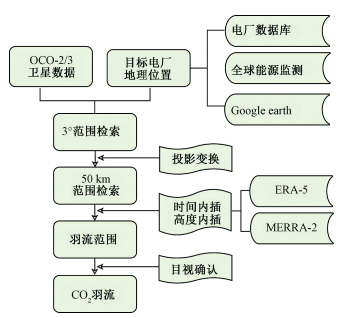
3 结果与讨论 3.1 电厂排放羽流筛选结果本研究以中国区域≥5 000 MW的超大型燃煤电厂为研究对象,按照附录图 A1所示步骤,共在托克托、外高桥和嘉兴电厂识别到7个CO2羽流(表 1)。以嘉兴电厂为例,首先下载OCO-2(2014-09-06—2021-10-01)和OCO-3(2019-08-06—2021-10-01)共3 669 d的数据,然后以电厂为中心做3°缓冲区,共检索到有观测记录的175个条带信息,其中127条来自OCO-2,48条来自OCO-3;下一步将检索出来的条带数据做投影变换,做50 km缓冲区,共识别出57条有充足数据点的条带,43条来自OCO-2,14条来自OCO-3;接着下载条带对应时间的风数据并插值到探测高度和探测时间,发现仅有9个条带距离嘉兴电厂较近(<10 km)并且与羽流区域相交;最后经过羽流可视化和目视确认,仅有1个条带记录到了XCO2增强信息。
|
|
表 1 7个羽流案例信息展示 Table 1 Seven plume case information display |
本研究根据每个羽流模拟时的大气参数,对3个电厂的CO2排放量进行估算。
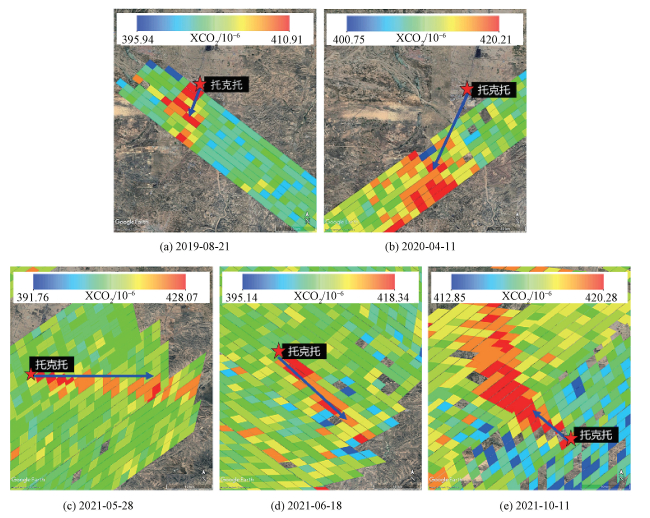
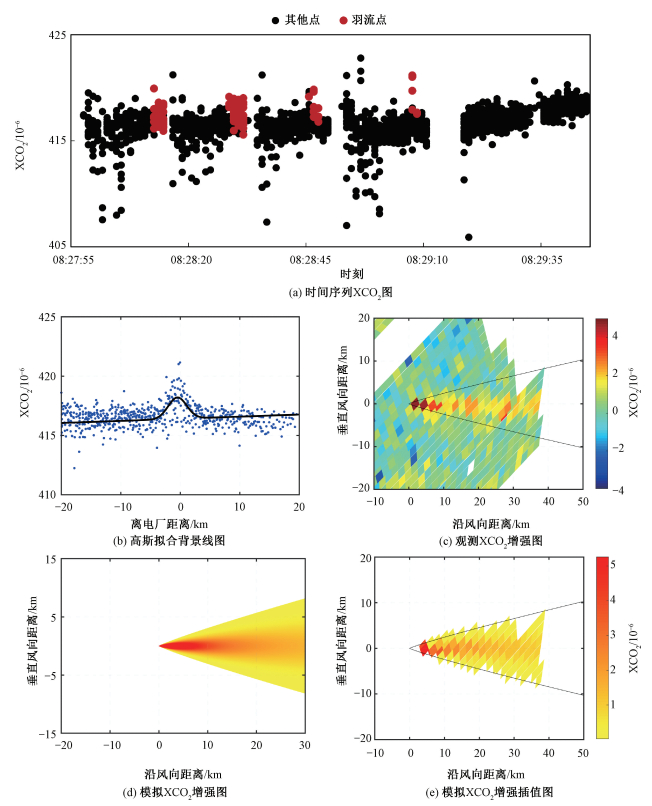
对于源强最大的托克托电厂,共识别到5个羽流信息,均来自OCO-3卫星(图 2)。以2021-05-28的CO2羽流为例(图 3),OCO-3卫星2 min内在电厂周围观测到6个条带,每个条带大约间隔20 s[23](图 3(a)),因为卫星经过时人为因素较少,呈现出较为干净的大气背景,高斯曲线拟合的背景值呈现出比其他2种方法更高的相关系数,如图 3(b)所示,蓝色的点为XCO2数据点,黑色的点高斯背景拟合线。此时OCO-3卫星清晰地记录下40 km左右的羽流底部和中心的形状,如图 3(c)中2条黑线之间的区域所示,并观测到约(0~4.5)×10-6的XCO2增强,模拟的CO2排放量为(76.48±15.75) kt/d,风向为274°时取得最大的相关系数(R=0.87)。这是托克托电厂估算值最高且相关系数最高的案例,最大的不确定性来源是气象数据不一致(14.03),另外还包括增强值(5.74)、背景值(4.09)和羽流上升(1.34 kt/d)。
|
Download:
|
| 箭头表示ERA5和MERRA-2平均风矢量,箭头的长度表示风矢量的大小。 图 2 托克托电厂附近的XCO2信息 Fig. 2 XCO2 information near Tuoketuo power plant | |
|
Download:
|
| 图 3 托克托电厂2021-05-28估算流程 Fig. 3 2021-05-28 estimation process for Tuoketuo Power Plant | |
另外4个羽流估算情况如表 2所示,综合这5个羽流案例,得到托克托电厂的加权平均CO2排放量为(62.48±12.92) kt/d(权重为相关系数),估算值与加权平均值的百分比差异最高为22.40%,最低为-31.42%,最高排放量为(76.48±15.75) kt/d,最低排放量为(42.85±3.24) kt/d。Nassar等[18]的研究中对同一发电厂的估计也存在类似的差异。
|
|
表 2 排放量估算情况 Table 2 Emission estimates |
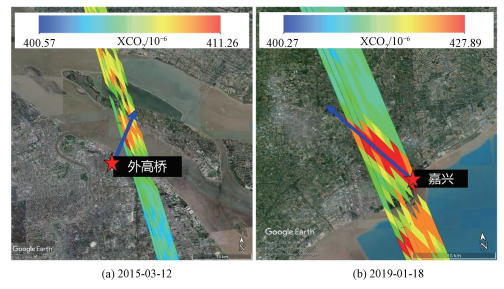
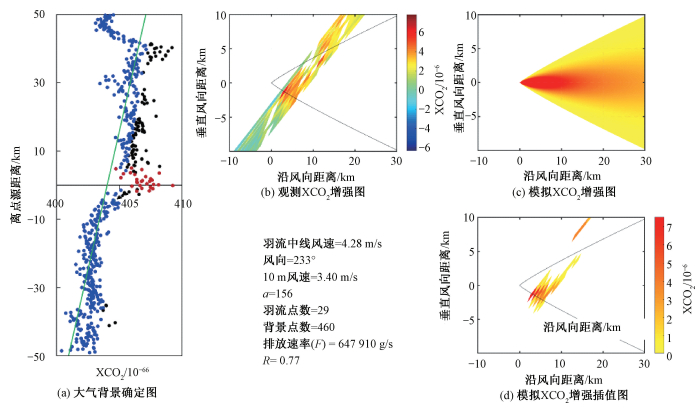
对于外高桥电厂,本研究共识别到1个CO2羽流(2015-03-12)(图 4(a)),OCO-2卫星于5:01分从距离电厂约2 km的上空飞过,识别到最高约5×10-6的强XCO2增强,风向大约为203°时取得最优相关系数(R=0.77),羽流范围内包括30个OCO-2探测点,模拟排放量(55.98±6.90) kt/d(附录图 A2)。不确定性主要因为2个气象场差别过大(5.78),其次为背景值(3.43),增强值(1.52)和羽流上升(0.42 kt/d)(表 3)。外高桥地处经济发达地带,人为影响因素比较大且处于水体和陆地交界处,考虑空间变异性的两步线性回归法估算相关系数最高。
|
Download:
|
| 图 4 外高桥、嘉兴电厂羽流可视化图 Fig. 4 Plume visualization of Waigaoqiao and Jiaxing Power Plants | |
|
|
表 3 不确定性来源与分析 Table 3 Sources and analysis of uncertainty |
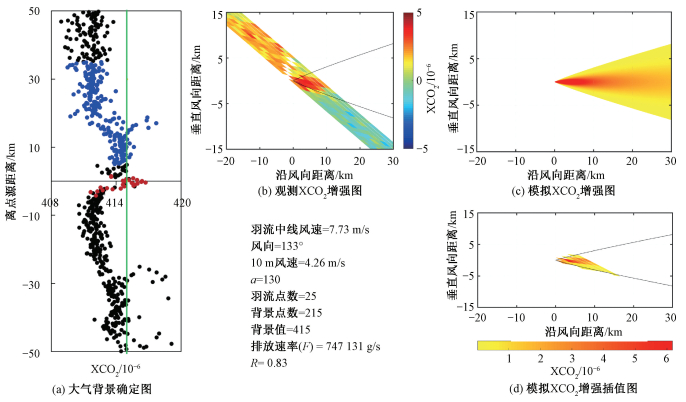
本研究在嘉兴电厂识别到1个CO2羽流(2019-01-18),OCO-2卫星于5:01从电厂正上方飞过,识别到平均2×10-6的XCO2增强,羽流区域内包括25个OCO-2探测点,模拟得到的CO2排放量为(64.55±15.89) kt/d,当风向调整至137°时相关系数最大(R=0.83)(图 5)。主要的不确定性来源是气象数据(14.31),其次为背景值(5.76),羽流上升(3.66)和增强值(1.00 kt/d)(表 3)。由于风的残余误差,导致其他方向出现一些增强,因此本案例适合不同背景值法,当取5~35 km的中值做背景值时显示出最优的相关系数,另外这是本研究唯一查找到全厂等效单源高度的电厂(507 m), 羽流上升不确定性为在此高度上下以50 m为间隔各取3个得到。
|
Download:
|
| 图 5 嘉兴电厂2019-01-18估算流程图 Fig. 5 Estimation flow chart of Jiaxing Power Plant on 2019-01-18 | |
综上,从7年OCO-2数据集和3年OCO-3数据集中识别到7个羽流,量化了中国区域内3个超大型燃煤电厂的CO2排放量。每个发电厂的羽流数量在1~5不等,估算CO2排放量在43~77 kt/d。单个羽流的不确定度在8%~32%(1σ)之间变化较大。其中气象数据是最大的不确定因素,占比集中在10%~20%。此外,大气背景值浓度是不确定性另一个主要来源,本研究综合采用3种方法确定背景值,这可能会增加不确定性的数值,但显著提高了高斯羽流模型模拟的相关系数,说明本研究确定的大气背景浓度更接近于真实情况。
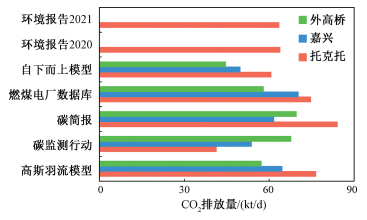
3.3 估算结果验证从CARMA、Carbon brief、GPED和企业发布环境报告(http://www.tuoxian.gov.cn/zwgk/tzgg/202203/t20220315_1202529.html)中提取相关电厂CO2排放信息,并利用IPCC提供的自下而上方法估算各电厂排放量(表 4)[37],用于高斯羽流模型估算的排放量对比验证。其中GPED记录的是截至2010年的电厂CO2排放信息,而3个电厂均在2010—2020年间增加新机组,本研究简单地将其按装机容量放大得到图 6[19]。在日尺度上,本研究中高斯羽流模型估算结果与其他方法或数据库在量级上呈现高度一致性,但数值上有所差异。
|
|
表 4 自下而上模型估算电厂排放量 Table 4 Power plant emissions estimated by bottom-up model |
|
Download:
|
| 图 6 CO2排放量对比验证 Fig. 6 CO2 emission comparison verification | |
对于托克托电厂,高斯羽流模型模拟的加权平均结果((62.48±12.92) kt/d)与托克托电厂公布的环境信息披露报告值(63.81,63.44 kt/d)以及自下而上模型估算值(60.66 kt/d)高度一致,但比CARMA(41.34 kt/d)偏高,比碳简报(84.08 kt/d)偏低(图 6)。主要原因是CARMA数据最新更新时间是2012年,此时装机容量仅为5 400 MW,而本文估算的时间均在2019年之后,装机容量为6 720 MW,CARMA的报告值仅为高斯羽流模型估算值的66%。另外CARMA估算电厂排放量时用城市中心的经纬度表示电厂经纬度[38],而本研究在进行估算时目标电厂的位置均经过谷歌地图目视确认,这也是出现差异的原因之一。而碳简报数据库对于每个电厂的估算没有根据不同地区和不同燃煤类型进行调整,托克托电厂虽然具有最大的装机容量,但2017年新增的2 000 MW机组为超超临界类型,其CO2排放因子要比之前的亚临界机组低,所以导致其估算结果可能会出现误差[39]。
对于外高桥和嘉兴电厂,高斯羽流模型估算结果((55.98±6.90),(64.55±15.89) kt/d)与其他排放清单一致性较高,差异均在估算的不确定性范围内,但比自下而上模型估算结果(44.60,49.73 kt/d)呈现明显的偏高趋势,主要原因可能在于自下而上模型中发电量主要根据CARMA报告值所得,由于CARMA记录统计值的滞后性[4],不能代表目前的排放情况。
综上,高斯羽流模型估算结果虽然与其他自下而上估计数值有所差异,但大部分都在估算的不确定性范围内。部分偏高的估计主要因为其他清单结果的更新时间及与高斯羽流模型估算的误差有关。但高斯羽流模型基于近实时卫星观测数据,表现出更高的时间分辨率和灵活性,可以广泛应用于世界各地工业点源的排放物估算。
3.4 改进本研究的改进之处主要体现在以下4方面:1)基于多源卫星数据(OCO-2和OCO-3)检索识别同一电厂的CO2羽流,提高了高斯羽流模型估算排放量的效率和可能性;2)综合采用3种方法确定背景值(表 5),结果更能代表发电厂的真实排放情况,通常情况下更大、更孤立的排放源因为较少受到人为活动影响,更适合用拟合高斯曲线法;但类似嘉兴电厂这种紧邻城市区域的电厂,目视确定背景值仍然是不可缺少的步骤;3)对于地形复杂地区的背景值确定,考虑了空间变异性的两步线性回归法显示出更强的相关性;另外本研究发现以多个羽流的加权平均排放量代替单个羽流排放估算值,可以有效降低单个估算的不确定度和偶然性,比如托克托加权平均CO2排放量为62.48 kt/d,与环境信息披露报告的百分比差异仅为2%,但2019-08-21的羽流估算值却高达49%。Hill和Nassar[40]指出随着羽流数量的增多,估算值将更准确,甚至可以从卫星的角度研究发电厂的日变化和季节变化;4)本研究考虑了羽流上升对于排放估算结果的影响,发现在多数案例估算中占比不大,但托克托电厂2021-10-11案例中羽流上升甚至超过了气象因素和背景因素成为主要因素,说明这部分不确定性不能被简单忽略[36]。
|
|
表 5 最优大气背景浓度确定 Table 5 Optimal atmospheric background concentration determination |
本研究整合OCO-2/3卫星数据识别中国区域超大型电厂CO2排放羽流,基于两步线性回归法、高斯曲线拟合法和不同背景范围法识别XCO2浓度增强,并利用高斯羽流模型反演CO2排放量。共从OCO-2和OCO-3数据集中识别到7个羽流,量化了中国3个超大型燃煤电厂的CO2排放量:托克托电厂((62.48±12.92) kt/d)、外高桥电厂((55.98±6.90) kt/d)和嘉兴电厂((64.55±15.89) kt/d)。使用2种气象数据,并考虑了羽流上升,以减少估算的不确定性。经过对比验证,高斯羽流模型结果与现有的与燃煤电厂数据库、碳监测行动以及碳简报等排放清单显示出很高的一致性,并且更能代表近年来的电厂排放情况。
本研究采用的方法能有效降低自下而上排放清单的数据误差和人为因素影响,可以广泛用于估计世界各地工业点源的碳排放量。未来,随着人为碳排放监测卫星的发射,高斯羽流模型将发挥更大的优势,甚至有望研究点源尺度上日排放和年排放信息及其变化趋势。
附录
|
Download:
|
| 图 A1 CO2羽流筛选流程图 Fig. A1 Flow chart of CO2 plume screening | |
|
Download:
|
| 图 A2 外高桥电厂2015-03-12估算流程图 Fig. A2 Estimation flow chart of Waigaoqiao Power Plant on 2015-03-12 | |
| [1] |
Keeling C D, Piper S. Exchanges of atmospheric CO2 and 13CO2 with the terrestrial biosphere and oceans from 1978 to 2000. Ⅳ. Critical overview[EB/OL]. Scripps Institution of Oceanography, (2001-06)[2023-03-30]. https://www.semanticscholar.org/paper/Exchanges-of-Atmospheric-CO2-and-13CO2-with-the-and-Keeling-Piper/de2acdfe1ea14d4605d0f9dd518d993e689fc8cf.
|
| [2] |
Friedlingstein P, Jones M W, O'Sullivan M, et al. Global carbon budget 2021[J]. Earth System Science Data, 2022, 14(4): 1917-2005. Doi:10.5194/essd-14-1917-2022 |
| [3] |
Liu L W, Chen C X, Zhao Y F, et al. China's carbon-emissions trading: overview, challenges and future[J]. Renewable and Sustainable Energy Reviews, 2015, 49: 254-266. |
| [4] |
Liu F, Zhang Q, Tong D, et al. High-resolution inventory of technologies, activities, and emissions of coal-fired power plants in China from 1990 to 2010[J]. Atmospheric Chemistry and Physics, 2015, 15(23): 13299-13317. Doi:10.5194/acp-15-13299-2015 |
| [5] |
Tong D, Zhang Q, Davis S J, et al. Targeted emission reductions from global super-polluting power plant units[J]. Nature Sustainability, 2018, 1(1): 59-68. Doi:10.1038/s41893-017-0003-y |
| [6] |
Gong S Y, Shi Y S. Evaluation of comprehensive monthly-gridded methane emissions from natural and anthropogenic sources in China[J]. Science of the Total Environment, 2021, 784: 147116. Doi:10.1016/j.scitotenv.2021.147116 |
| [7] |
Lei R X, Feng S, Danjou A, et al. Fossil fuel CO2 emissions over metropolitan areas from space: a multi-model analysis of OCO-2 data over Lahore, Pakistan[J]. Remote Sensing of Environment, 2021, 264: 112625. Doi:10.1016/j.rse.2021.112625 |
| [8] |
Ahn D Y, Hansford J R, Howe S T, et al. Fluxes of atmospheric greenhouse-gases in Maryland (FLAGG-MD): emissions of carbon dioxide in the Baltimore, MD-Washington, D.C. area[J]. Journal of Geophysical Research: Atmospheres, 2020, 125(9): e2019JD032004. Doi:10.1029/2019jd032004 |
| [9] |
Whetstone J R. Advances in urban greenhouse gas flux quantification: the indianapolis flux experiment (INFLUX)[J]. Elementa: Science of the Anthropocene, 2018, 6: 24. Doi:10.1525/elementa.282 |
| [10] |
Krings T, Gerilowski K, Buchwitz M, et al. MAMAP-a new spectrometer system for column-averaged methane and carbon dioxide observations from aircraft: retrieval algorithm and first inversions for point source emission rates[J]. Atmospheric Measurement Techniques, 2011, 4(9): 1735-1758. Doi:10.5194/amt-4-1735-2011 |
| [11] |
Krings T, Neininger B, Gerilowski K, et al. Airborne remote sensing and in situ measurements of atmospheric CO2 to quantify point source emissions[J]. Atmospheric Measurement Techniques, 2018, 11(2): 721-739. Doi:10.5194/amt-11-721-2018 |
| [12] |
Hirofumi O, Kei S, Nobuhiro K, et al. Quantifying CO2 emissions from a thermal power plant based on CO2 column measurements by portable Fourier transform spectrometers[J]. Remote Sensing of Environment, 2021, 267. Doi:10.1016/J.RSE.2021.112714 |
| [13] |
Zhou M Q, Ni Q C, Cai Z N, et al. CO2 in Beijing and Xianghe observed by ground-based FTIR column measurements and validation to OCO-2/3 satellite observations[J]. Remote Sensing, 2022, 14(15): 3769. Doi:10.3390/rs14153769 |
| [14] |
吴长江, 雷莉萍, 曾招城. 不同卫星反演的大气CO2浓度差异时空特征分析[J]. 中国科学院大学学报, 2019, 36(3): 331-337. Doi:10.7523/j.issn.2095-6134.2019.03.006 |
| [15] |
Ye X X, Lauvaux T, Kort E A, et al. Constraining fossil fuel CO2 emissions from urban area using OCO-2 observations of total column CO2[J]. Journal of Geophysical Research: Atmospheres, 2020, 125(8): 1-29. Doi:10.1029/2019jd030528 |
| [16] |
Zheng B, Chevallier F, Ciais P, et al. Observing carbon dioxide emissions over China's cities and industrial areas with the Orbiting Carbon Observatory-2[J]. Atmospheric Chemistry and Physics, 2020, 20(14): 8501-8510. Doi:10.5194/acp-20-8501-2020 |
| [17] |
Nassar R, Hill T G, McLinden C A, et al. Quantifying CO2 emissions from individual power plants from space[J]. Geophysical Research Letters, 2017, 44(19): 10,045-10,053. Doi:10.1002/2017gl074702 |
| [18] |
Nassar R, Mastrogiacomo J-P, Bateman-Hemphill W, et al. Advances in quantifying power plant CO2 emissions with OCO-2[J]. Remote Sensing of Environment, 2021, 264: 112579. Doi:10.1016/j.rse.2021.112579 |
| [19] |
Hu Y Q, Shi Y S. Estimating CO2 Emissions from large scale coal-fired power plants using OCO-2 observations and emission inventories[J]. Atmosphere, 2021, 12(7): 811. Doi:10.3390/atmos12070811 |
| [20] |
Zheng T, Nassar R, Baxter M. Estimating power plant CO2 emission using OCO-2 XCO2 and high resolution WRF-Chem simulations[J]. Environmental Research Letters, 2019, 14(8): 085001. Doi:10.1088/1748-9326/ab25ae |
| [21] |
Crisp D, Pollock H R, Rosenberg R, et al. The on-orbit performance of the Orbiting Carbon Observatory-2 (OCO-2) instrument and its radiometrically calibrated products[J]. Atmospheric Measurement Techniques, 2017, 10(1): 59-81. Doi:10.5194/amt-10-59-2017 |
| [22] |
Eldering A, Taylor T E, O'Dell C W, et al. The OCO-3 mission: measurement objectives and expected performance based on 1 year of simulated data[J]. Atmospheric Measurement Techniques, 2019, 12(4): 2341-2370. Doi:10.5194/amt-12-2341-2019 |
| [23] |
Kiel M, Eldering A, Roten D D, et al. Urban-focused satellite CO2 observations from the Orbiting Carbon Observatory-3: a first look at the Los Angeles megacity[J]. Remote Sensing of Environment, 2021, 258: 112314. Doi:10.1016/j.rse.2021.112314 |
| [24] |
MacDonald C G, Mastrogiacomo J P, Laughner J L, et al. Estimating enhancement ratios of nitrogen dioxide, carbon monoxide and carbon dioxide using satellite observations[J]. Atmospheric Chemistry and Physics, 2023, 23(6): 3493-3516. Doi:10.5194/acp-23-3493-2023 |
| [25] |
其其格, 卢晓东. 浅析托克托电厂对环境的影响及其防治措施[J]. 干旱区资源与环境, 2004, 18(S3): 63-68. |
| [26] |
陈仁杰. 上海外高桥第三发电厂工程设计特点[J]. 电力勘测设计, 2010(3): 34-38. Doi:10.3969/j.issn.1671-9913.2010.03.009 |
| [27] |
顾澎. 浙江嘉兴发电厂三期工程设计的项目化管理研究[D]. 北京: 华北电力大学, 2011.
|
| [28] |
Pollock R, Haring R E, Holden J R, et al. The Orbiting Carbon Observatory instrument: performance of the OCO instrument and plans for the OCO-2 instrument[C]//Proc SPIE 7826, Sensors, Systems, and Next-Generation Satellites XIV, 2010, 7826: 241-253. DOI: 10.1117/12.865243.
|
| [29] |
Taylor T E, Eldering A, Merrelli A, et al. OCO-3 early mission operations and initial (vEarly) XCO2 and SIF retrievals[J]. Remote Sensing of Environment, 2020, 251: 112032. Doi:10.1016/j.rse.2020.112032 |
| [30] |
Lin J S, Hildemann L M. Analytical solutions of the atmospheric diffusion equation with multiple sources and height-dependent wind speed and eddy diffusivities[J]. Atmospheric Environment, 1996, 30(2): 239-254. Doi:10.1016/1352-2310(95)00287-9 |
| [31] |
Hersbach H, Bell B, Berrisford P, et al. The ERA5 global reanalysis[J]. Quarterly Journal of the Royal Meteorological Society, 2020, 146(730): 1999-2049. Doi:10.1002/qj.3803 |
| [32] |
Gelaro R, McCarty W, Suárez M J, et al. The modern-era retrospective analysis for research and applications, version 2 (MERRA-2)[J]. Journal of Climate, 2017, 30(14): 5419-5454. Doi:10.1175/jcli-d-16-0758.1 |
| [33] |
Afsah S, Ness E. Carbon monitoring for action (CARMA): climate campaign built on questionable data-a due diligence report on CARMA's data and methodology[J]. SSRN Electronic Journal, 2008, 1133432. Doi:10.2139/ssrn.1133432 |
| [34] |
Brusca S, Famoso F, Lanzafame R, et al. Theoretical and experimental study of Gaussian plume model in small scale system[J]. Energy Procedia, 2016, 101: 58-65. Doi:10.1016/j.egypro.2016.11.008 |
| [35] |
杨文燕, 宋长春, 张金波. 三江平原小叶章和毛果苔草两种地表覆被下的贴地气层CO2浓度垂直分布特征[J]. 中国科学院研究生院学报, 2006, 23(5): 686-691. Doi:10.7523/j.issn.2095-6134.2006.5.020 |
| [36] |
Brunner D, Kuhlmann G, Marshall J, et al. Accounting for the vertical distribution of emissions in atmospheric CO2 simulations[J]. Atmospheric Chemistry and Physics, 2019, 19(7): 4541-4559. Doi:10.5194/acp-19-4541-2019 |
| [37] |
Paustian K, Ravindranath N H, Amstel A V. 2006 IPCC guidelines for national greenhouse gas inventories[R]. Environmental Science, 2006.
|
| [38] |
Wheeler D, Ummel K. Calculating carma: Global estimation of CO2 emissions from the power sector[J]. SSRN Electronic Journal, 2008, 1138690. Doi:10.2139/ssrn.1138690 |
| [39] |
马学礼, 王笑飞, 孙希进, 等. 燃煤发电机组碳排放强度影响因素研究[J]. 热力发电, 2022, 51(1): 190-195. Doi:10.19666/j.rlfd.202108176 |
| [40] |
Hill T, Nassar R. Pixel size and revisit rate requirements for monitoring power plant CO2 emissions from space[J]. Remote Sensing, 2019, 11(13): 1608. Doi:10.3390/rs11131608 |
 2024, Vol. 41
2024, Vol. 41 


