2. 中国科学院大学,北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
太阳能电池阵作为卫星的能源供应系统,其性能好坏直接决定了在轨卫星能否正常稳定运行。据文献统计[1],近50年来公开发布的国内外航天器发射与在轨故障的发生原因中,有21% 是由于电源分系统故障导致,因此对太阳能电池阵进行异常检测具有重大意义。卫星遥测数据是地面工作站对卫星运行状态进行判断的唯一依据[2],因此根据历史遥测数据的变化规律对卫星未来工作状态趋势进行预测,并根据预测结果对卫星性能状态进行评估,对确保卫星健康稳定运行具有重大意义。目前,对遥测数据进行异常检测,工程上一直采用传统的人工数据判读、阈值自动判读以及专家经验手段进行[3]。针对基于预测模型的异常检测方法,由于传统的阈值自动判读方法具有方法简单且易实施、拥有较好的效果等优点,被广泛应用于实际场景中,因而预测模型的精确度决定了遥测数据异常检测的准确性。
在时序数据预测领域,传统的模型,如卡尔曼滤波[4-5]、自回归移动平均模型(ARMA)[6]、自回归差分移动平均模型(ARIMA)[7]等都具有广泛的应用。近年来,随着机器学习和深度学习的不断发展,该领域的相关方法被成功应用到了时序预测领域,如:人工神经网络(ANN)[8-10]、支持向量机(SVM)[11],其中,长短期记忆网络(long short-term memory,LSTM)由于具有较好的时序特征提取能力,在时序数据预测领域得到了广泛关注。文献[12-14]使用LSTM对时间序列进行预测,但传统预测模型仅通过LSTM对具有高频动态波动时序数据进行建模,存在预测精度不足问题,难以对平稳变化数据和高频动态波动数据同时进行良好建模。文献[15-17]在LSTM的基础上引入小波变换,以增强数据特征,提高LSTM模型的预测精度,但单通道LSTM模型对序列特征表达能力有限,难以对特征进行全面表达,而双通道LSTM模型可以提高特征表达能力,最终提高预测精度。
卫星太阳能电池阵输入电流数据是时序数据,因此具有较强的时序特征,同时由于卫星电池阵所处的环境恶劣,受外界影响较多,会造成电流的波动起伏。鉴于小波变换的多尺度分析特性以及LSTM的时序特征提取能力,同时双通道能够更加有效地提取出时序特征信息。本文提出一种基于离散小波变换的双通道LSTM预测模型,不直接预测信号本身,而是预测信号的小波系数,再对小波系数进行信号重构,最终获得预测信号。在某卫星上的真实遥测数据上进行模型性能验证,结果表明,相较于传统的LSTM预测模型,本文所提方法具有更好的预测性能。
1 基础理论 1.1 LSTM原理结构LSTM是RNN的一种特殊类型,可以解决传统RNN存在的梯度消失或梯度爆炸问题。这意味着LSTM在处理较长时序数据时,尤其在捕获长期依赖关系和进行非线性变换方面具有更强的优势,因此其在时序数据预测领域具有广泛的应用。具体模型如图 1所示。

|
Download:
|
| 图 1 LSTM单元结构示意图 Fig. 1 Schematic diagram of LSTM unit structure | |
LSTM通过使用精心设计的结构来解决RNN存在的梯度问题。在LSTM单元中,ht可以认为是一个短期状态,Ct可以认为是一个长期状态。LSTM的独特之处在于可以通过“门”结构对信息进行控制,决定哪些信息需要被存储,哪些信息可以被遗忘,哪些信息需要添加更新。LSTM工作原理表达式如下所示:
| $ f_t=\sigma\left(\boldsymbol{W}_{\mathrm{f}} \cdot\left[\boldsymbol{h}_{t-1}, \boldsymbol{x}_t\right]+\boldsymbol{b}_{\mathrm{f}}\right), $ | (1) |
| $ \boldsymbol{i}_t=\sigma\left(\boldsymbol{W}_{\mathrm{i}} \cdot\left[\boldsymbol{h}_{t-1}, \boldsymbol{x}_t\right]+\boldsymbol{b}_{\mathrm{i}}\right), $ | (2) |
| $ \tilde{\boldsymbol{C}}_t=\tanh \left(\boldsymbol{W}_{\mathrm{c}} \cdot\left[\boldsymbol{h}_{t-1}, \boldsymbol{x}_t\right]+\boldsymbol{b}_{\mathrm{c}}\right), $ | (3) |
| $ {\mathit{\boldsymbol{C}}_t} = {\mathit{\boldsymbol{f}}_t}*{\mathit{\boldsymbol{C}}_{t - 1}} + {\mathit{\boldsymbol{i}}_t}*{\mathit{\boldsymbol{\tilde C}}_t}, $ | (4) |
| $ {\mathit{\boldsymbol{o}}_t} = \sigma \left( {{\mathit{\boldsymbol{W}}_{\rm{o}}} \cdot \left[ {{\mathit{\boldsymbol{h}}_{t - 1}}, {\mathit{\boldsymbol{x}}_t}} \right] + {\mathit{\boldsymbol{b}}_{\rm{o}}}} \right), $ | (5) |
| $ \boldsymbol{h}_t=\boldsymbol{o}_t * \tanh \left(\boldsymbol{C}_t\right) . $ | (6) |
式中:Wf、Wi、Wc和Wo分别为遗忘门、输入门、当前单元状态和输出门的权重矩阵;bf、bi、bc和bo分别为对应的偏置项;σ表示sigmoid激活函数;xt为t时刻的输入,ht-1表示t-1时刻输出,Ct-1和Ct分别表示t-1时刻和t时刻的单元状态,
ft表示遗忘门输出,决定了上一时刻长期记忆单元状态Ct-1信息的遗忘程度;it为输入门输出,决定了当前输入xt的情况下信息更新到Ct的情况;ot表示输出门输出,控制单元状态Ct到LSTM的当前输出值ht。
1.2 离散小波变换小波变换相较于傅里叶变换,不同之处在于基函数的不同,小波变换将傅里叶变换的基函数替换成了有限长会衰减的小波基。小波变换的优势在于既可以提取时域特征,也可以提取频域特征,具有较强的时频特征表达能力,对于非平稳信号具有较强的分析能力,不同的低频小波系数表征了对应尺度的数据偏差,因而小波分解可以提高一维数据特征。
离散小波变换(discrete wavelet transform, DWT)采用Mallat快速算法实现,该算法是一个采用小波滤波器对离散信号进行多次低通和高通滤波的过程,每次滤波获得一个低频分量和一个高频分量。设第i尺度上的低频分量为ai,高频分量为di,正交小波滤波器分别为h(低通)和g(高通),则某一尺度上的小波分解和合成的Mallat算法可表示为:
| $ a_i(k)=\sum\limits_n h(n-2 k) a_{i-1}(n), $ | (7) |
| $ d_i(k)=\sum\limits_n g(n-2 k) a_{i-1}(n), $ | (8) |
| $ a_{i-1}(n)=\sum\limits_k h(n-2 k) a_i(k)+\sum\limits_k g(n-2 k) d_i(k) . $ | (9) |
卫星太阳能电池阵电流受外在因素以及内在因素两方面影响。内在因素一般包括电池阵电池片的转化效率、温度变化特性以及因太空环境而造成的衰减和突变等因素。外在因素一般包括太阳光强度、太阳光入射角、卫星姿态变化以及遮挡和反照等因素。这些因素都会对太阳能电池阵电流数据变化产生影响,且具有一定的叠加效果,因此太阳能电池阵电流数据可能存在较多的波动。
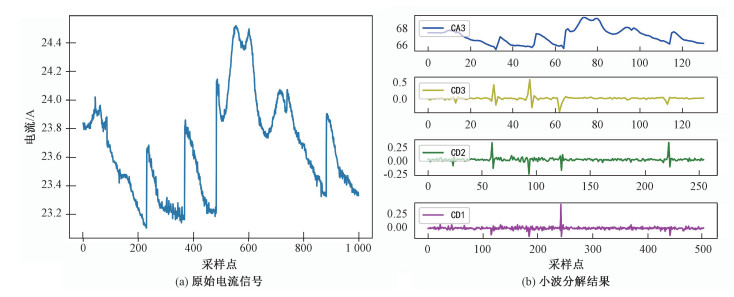
对本文采用的太阳能电池阵电流数据取部分长度序列进行3层小波分解,分解结果如图 2所示。
|
Download:
|
| 图 2 原始电流信号及小波分解结果 Fig. 2 Original current signal and wavelet decomposition results | |
从图 2(a)可以看出,原始电流信号具有很多高频的微小动态,由于LSTM对扰动比较敏感,若直接通过LSTM对其进行特征提取并建模,则较难对信号趋势以及高频动态同时进行建模,因此会造成预测精度不足的问题。对信号进行3层小波分解后,得到不同的小波系数,如图 2(b)所示。低频小波系数CA3很好地反映了信号的总体趋势且无扰动,因此易对其进行建模,具有较高的可预测性。小波分解得到的不同层高频小波系数CD1、CD2和CD3分别反映了不同尺度上的动态信息,且高频小波系数相互正交,对每层高频系数使用LSTM单独进行建模,可以降低单个LSTM模型复杂度,降低扰动对模型建模精度的影响,从而提高模型对信号的适应度以及提高模型的预测精度。
2.2 预测模型LSTM具有较好的时序特征提取能力,因此在时序数据预测领域上具有较强优势。而双通道LSTM模型通过对不同隐藏层设置不同数量的神经元,可以捕捉不同信息特征,从而加强对特征的提取能力。但对于变化频率较高且较复杂的信号而言,LSTM存在特征表达能力不足问题。小波分解可以根据信号的时频特性,以多层小波系数对数据时频特征进行表征,加强数据特征,降低数据复杂度。本文结合LSTM和小波分解的优点,在LSTM的基础上引入小波分解来提高数据特征,降低单个模型的建模复杂度,解决传统单通道LSTM对变化频率较高的复杂信号预测精度不足的问题。
本文所提出的预测模型如图 3所示。模型主要包含以下3部分:1)对单通道遥测数据进行归一化操作后再进行3阶小波分解,从而获取不同尺度的小波系数;2)对小波分解得到的多层小波系数分别通过双通道LSTM网络进行时序特征提取并进行预测;3)对预测出来的各层小波系数进行逆小波变换得到重构信号,之后对重构信号进行反归一化,从而获得最终的预测值。

|
Download:
|
| 图 3 预测模型流程图 Fig. 3 Flow chart of prediction model | |
本实验是基于Windows操作系统,深度学习框架选用TensorFlow计算框架,CPU为Intel I5-4200H, 2.80 GHz, tensorflow为1.13.1版本,keras为2.3.1版本,numpy为1.15.4版本,pandas为0.23.4版本,pywavelets为1.1.1版本。本实验采用CPU进行模型训练和测试。
3.1 数据集介绍及模型参数设置实验采用某卫星型号的+y轴电池阵电流遥测数据作为实验数据集,数据点采样频率为0.125 Hz,共134 773个数据点,采用滑窗法按固定窗口大小获取实验所需数据集。取步长lp为LSTM模型输出数据的时间长度,预测时间步长越长,预测精度越差,为保证模型的预测精度,本文选取lp=1。将数据集按照比例0.7 ∶0.1 ∶0.2划分为训练集、验证集和测试集。网络模型部分参数如表 1所示。
|
|
表 1 模型参数 Table 1 Model parameters |
为评价模型的性能,引入回归任务中常用评价指标,分别为平均绝对误差MAE,均方根误差RMSE和相关系数R。
| $ \mathrm{MAE}=\frac{\sum\limits_{t=1}^N\left|y_t-\hat{y}_t\right|}{N}, $ | (10) |
| $ \mathrm{RMSE}=\sqrt{\frac{\sum\limits_{t=1}^N\left|y_t-\hat{y}_t\right|}{N}}, $ | (11) |
| $ R=\frac{\operatorname{Cov}(y, \hat{y})}{\sqrt{V(y)} \sqrt{V(\hat{y})}} . $ | (12) |
式中:
表 2为隐藏层具有不同大小units设置的LSTM预测模型的性能比较,隐藏层units设置分别为80-80和64-32,其中80-80表示第1层隐藏层和第2层隐藏层的units数量设置。如表 2所示,对于单通道模型,不同units设置的LSTM预测模型在评价指标上具有不同结果,反映了不同units设置的LSTM模型对信号特征具有不同的关注点和提取能力。表中实验结果数据显示,结合具有不同units数量设置的双通道模型在RMSE和R的性能指标上较2个单通道模型都有明显提升,而在MAE上表现与较好的模型一致。由于RMSE对异常值的敏感度更高,RMSE降低说明双通道模型预测值和实际值的偏离程度降低,因而预测精度更高,而R指标提高说明双通道模型对数据的拟合度更高。该结果表明在双通道模型中,能够综合具有不同units的预测模型的优点,提高模型的特征提取能力,从而提高模型的预测性能。
|
|
表 2 不同units设置的LSTM预测模型性能比较 Table 2 Performance comparison of LSTM prediction models with different units |
表 3为不同模型的网络结构配置和预测性能比较。从表 3可以看出,本文提出的DWT-DoubleLSTM预测模型获得了最好的预测结果,各性能评价指标具有不同程度的提升。对于单通道模型,基于小波变换的DWT-LSTM相较于传统LSTM,其MAE减少5.7%,RMSE减少15.4%,R提高1.8%;基于小波变换的DWT-DoubleLSTM模型相较于传统LSTM模型,其MAE减少16.4%,RMSE减少29.9%,R提高3.2%。该结果表明,通过对信号进行小波分解,得到多层小波系数,并对每层系数单独建模,将单个预测任务分解为多个预测任务,可以有效降低模型复杂度,从而有效提高最终的预测精度。而基于小波变换的DWT-LSTM的预测效果没有Double-LSTM好,但比传统单通道LSTM预测效果好,说明使用双通道融合可以加强模型对特征的提取能力,提高模型的预测能力。
|
|
表 3 不同预测模型的网络结构 Table 3 Network structure of different prediction models |
图 4为部分时间的各层小波系数预测结果图。从图 4中结果可以看出,图 4(a)第3层低频系数上的预测效果较好,低频系数反映了信号的总体趋势,且无小动态,因而神经网络模型对其建模预测较为简单。其他3层高频系数预测值和真实值不能完全一一对应,但总体趋势一致以及误差范围能限定在一个较小的值。由于低频系数预测准确率较高,而高频系数预测模型将预测误差限定在了一个很小的范围内,因此对预测小波系数做小波重构时,能够恢复出良好的信号而不具有大误差。

|
Download:
|
| 图 4 各层小波系数预测值 Fig. 4 Prediction results of different wavelet coefficients | |
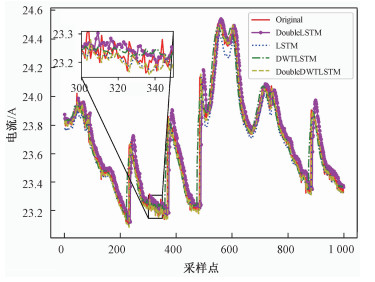
图 5为局部时间各种预测模型的预测结果图。从图 5的各种模型预测结果可以看出,基于小波变换的DWT-DoubleLSTM预测模型,无论是总体趋势还是细节预测精度,都比其他模型高,反映了使用小波分解方法获得多层小波系数,并对多层小波系数分别建模预测的方法能够降低信号复杂度和单个模型建模复杂度的正确性。
|
Download:
|
| 图 5 不同预测模型的预测结果图 Fig. 5 The prediction results of different prediction models | |
为解决卫星太阳能电池阵电流预测精度不足问题,本文提出基于DWT和双通道LSTM的数据预测模型,并通过使用某卫星型号的真实遥测数据对模型进行实验验证。结果表明,双通道LSTM在数据预测效果上相较于单通道LSTM有一定的提升;通过离散小波变换对时间序列进行小波分解之后,再对小波系数进行预测,最后使用预测小波系数重构出预测值。该方法相较于传统的直接使用LSTM预测信号取得了更好的预测效果。最终结果表明本文所提出的方法相较于传统使用LSTM直接对信号进行预测具有更高的预测性能,其MAE减少16.4%,RMSE减少29.9%,R提高3.2%。但本文未考虑特征之间的相关性以及时序数据的时间相关性对信号预测的影响,因此后续研究将对多信号输入下的遥测数据预测工作展开研究,同时对LSTM引入attention机制加强模型的特征提取能力,提高模型的预测精度。
| [1] |
王嘉轶, 闻新. 航天器故障诊断技术的研究现状与进展[J]. 航空兵器, 2016(5): 71-76. Doi:10.19297/j.cnki.41-1228/tj.2016.05.014 |
| [2] |
董静怡, 庞景月, 彭宇, 等. 集成LSTM的航天器遥测数据异常检测方法[J]. 仪器仪表学报, 2019, 40(7): 22-29. Doi:10.19650/j.cnki.cjsi.J1904832 |
| [3] |
彭喜元, 庞景月, 彭宇, 等. 航天器遥测数据异常检测综述[J]. 仪器仪表学报, 2016, 37(9): 1929-1945. Doi:10.19650/j.cnki.cjsi.2016.09.002 |
| [4] |
修春波, 任晓, 李艳晴, 等. 基于卡尔曼滤波的风速序列短期预测方法[J]. 电工技术学报, 2014, 29(2): 253-259. Doi:10.19595/j.cnki.1000-6753.tces.2014.02.031 |
| [5] |
刘星, 吕孝雷. 基于卡尔曼滤波的PS-InSAR地表形变预测方法[J]. 中国科学院大学学报, 2017, 34(6): 743-750. Doi:10.7523/j.issn.2095-6134.2017.06.011 |
| [6] |
Huang R, Huang T, Gadh R, et al. Solar generation prediction using the ARMA model in a laboratory-level micro-grid[C]//2012 IEEE Third International Conference on Smart Grid Communications (SmartGridComm). Tainan, Taiwan, China: IEEE, 2012: 528-533. DOI: 10.1109/SmartGridComm.2012.6486039.
|
| [7] |
Anwar M Y, Lewnard J A, Parikh S, et al. Time series analysis of malaria in Afghanistan: using ARIMA models to predict future trends in incidence[J]. Malaria Journal, 2016, 15(1): 566. Doi:10.1186/s12936-016-1602-1 |
| [8] |
Vui C S, Soon G K, On C K, et al. A review of stock market prediction with Artificial neural network (ANN)[C]//2013 IEEE International Conference on Control System, Computing and Engineering. Penang, Malaysia: IEEE, 2013: 477-482. DOI: 10.1109/ICCSCE.2013.6720012.
|
| [9] |
Ma D L, Zhou T, Chen J, et al. Supercritical water heat transfer coefficient prediction analysis based on BP neural network[J]. Nuclear Engineering and Design, 2017, 320: 400-408. Doi:10.1016/j.nucengdes.2017.06.013 |
| [10] |
田玮, 朱廷劭. 基于深度学习的微博用户自杀风险预测[J]. 中国科学院大学学报, 2018, 35(1): 131-136. Doi:10.7523/j.issn.2095-6134.2018.01.018 |
| [11] |
王剑非, 姜斌, 冒泽慧. 基于LSSVM的卫星姿态控制系统故障诊断[J]. 控制工程, 2008, 15(3): 334-336, 341. Doi:10.14107/j.cnki.kzgc.2008.03.010 |
| [12] |
Hundman K, Constantinou V, Laporte C, et al. Detecting spacecraft anomalies using LSTMs and nonparametric dynamic thresholding[C]//Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York, NY, USA: ACM, 2018: 387-395. DOI: 10.1145/3219819.3219845.
|
| [13] |
Li T Y, Comer M, Delp E, et al. A stacked predictor and dynamic thresholding algorithm for anomaly detection in spacecraft[C]//2019 IEEE Military Communications Conference (MILCOM 2019). Norfolk, VA, USA: IEEE, 2019: 165-170. DOI: 10.1109/MILCOM47813.2019.9021055.
|
| [14] |
简献忠, 顾洪志, 王如志. 一种基于双通道CNN和LSTM的短期光伏功率预测方法[J]. 电力科学与工程, 2019, 35(5): 7-11. Doi:10.3969/j.ISSN.1672-0792.2019.05.002 |
| [15] |
孙铭, 魏守科, 王莹洁, 等. 基于小波分解的LSTM水质预测模型[J]. 计算机系统应用, 2020, 29(12): 55-63. Doi:10.15888/j.cnki.cas.007695 |
| [16] |
何哲祥, 李雷. 基于小波变换和LSTM的大气污染物浓度预测模型[J]. 环境工程, (2020-11-27)[2021-03-19]. http://kns.cnki.net/kcms/detail/11.2097.X.20201126.1858.002.html.
|
| [17] |
杨梅, 李忠, 吴昊. 基于多尺度时间特征的LSTM短期负荷预测[J]. 控制工程, 2022, 29(9): 1722-1728. Doi:10.14107/j.cnki.kzgc.20200542 |
 2023, Vol. 40
2023, Vol. 40 


