空间机器人[1]在轨维护任务[2-3]首先需要对目标完成识别和测量[4],该任务对测量精度、运算效率、容错率、计算资源等提出更高要求。利用轻量化视觉相机[5]开展非合作目标相对位姿测量[6],具有抗干扰、易开发、高分辨率等优势,是未来低成本、高精准在轨观测领域的重点研究方向之一。
空间相对位姿测量核心包括空间位姿描述与坐标变换,三维点云配准有助于解决该问题。经典解决点云配准的ICP算法[7](iterative closest point, ICP)存在局部最优和计算效率低的问题。目前点云配准研究一般分为基于特征点的方法、基于优化的方法和基于机器学习[8]的方法等。其中,基于特征点易陷入局部最优且计算效率低,基于机器学习的方法精度更高但计算量较大。一些学者融入特征进行改进[9]能够提高配准精度与效率。例如:周颖和林意[10]提出一种基于法向量投票的点云配准算法,提高了配准精度;陶海跻和达飞鹏[11]提出一种基于点云法向量的自动配准算法具备自适应的优势。此外,研究人员还在探索整合相机等传感器深度数据的方法,以提高算法性能。例如,韩一菲等[12]利用飞行时间(time of flight, TOF)原理获取点云的相关特征,提出一种适用于TOF点云的改进ICP配准算法,从而达到提高观测精度的目的。
由于空间环境的特殊性,非合作目标存在目标被遮挡、局部信息丢失的问题,需要重点研究。对此,石峰源等[13]提出基于TOF相机的霍夫变换点云配准改进算法,以某卫星部件完整及残缺模型为例进行实验,验证了其对于残缺目标配准的可行性与鲁棒性;卢祺等[14]提出二维图像优化三维点云聚类的方法,能够解决特征相似部分无法聚类识别的问题,但该法受光照影响较大,需在特定环境适用;Ding和He[15]使用深度相机,以等距的不同角度对特定场景下的目标进行采样,利用SAC-IA和ICP算法获取场景中非合作目标的位姿信息。上述文献通常仅针对卫星部件、空间非合作目标点云模型等,缺乏普适性,算法在遮挡和杂乱环境等现实场景中的实验与分析仍待加强。
本文重点针对空间机器人在轨维修等任务中的非合作目标位姿估计问题,基于低成本的TOF相机抗干扰的优势,提出一种基于点云配准的空间非合作目标位姿估计算法。经地面缩比实验验证,本文算法的响应速度快、容错率高,姿态角测量误差小于0.4°,位移测量误差小于3 mm,是一种针对空间相对测量问题的有效解决手段。
1 问题分析与优化思路 1.1 问题分析星载计算机算力有限条件下的空间目标配准任务,受配准初始值、弱光环境等影响,存在局部最优、配准效果有待提高等问题。
1.2 优化思路针对空间非合作目标观测受光照影响的问题,本研究选用TOF相机作为测量敏感器获得观测信息,通过主动发射光信号获取目标深度信息,实现对目标三维点云的提取。相比利用目标的颜色和纹理信息进行识别的传统深度相机,TOF相机受光照影响较小,测量精度较高。
受太空环境影响,获取的点云噪声较大、离群点分布不均,单一滤波算法难以满足空间非合作目标点云预处理的需求。为防止星载计算机运行过载,对TOF相机提取到的点云数据进行预处理。本文采用体素网格重心滤波和KD-Tree[16]均值滤波的复合滤波算法,在保持目标特征的前提下有效降低点云密度,减轻计算负担,提高配准效率。
空间非合作目标中的卫星、空间站等航天器大多具备外形对称的特点,易导致配准失误,特征向量匹配可以在提高配准效率的前提下提高配准精度、降低误配率。建立匹配关系后,利用RANSAC算法[17]校验外点,检验特征点的匹配效果,删除误匹配点。
基于上述粗配准环节在特征点匹配与校验方面的优化,在精配准阶段引入改进的ICP配准算法,有利于进一步得到良好的配准效果[18]。
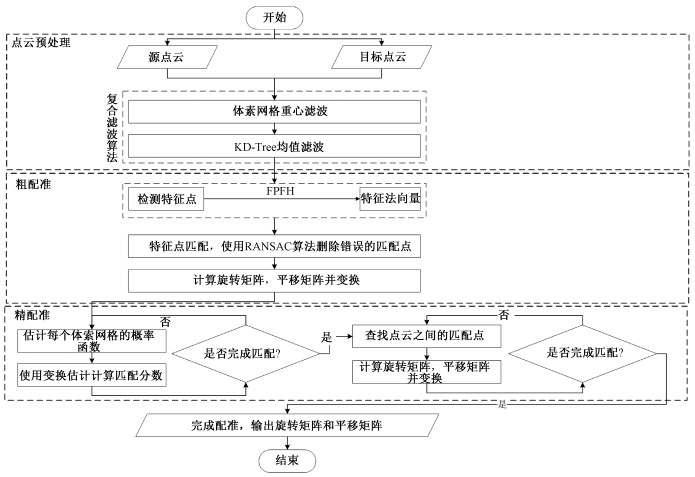
2 算法设计基于点云配准的空间非合作目标位姿估计算法总流程图如图 1所示。
|
Download:
|
| 图 1 一种基于点云配准的空间非合作目标位姿估计算法总体流程图 Fig. 1 The overall flow chart of a spatial non-cooperative target pose estimation algorithm based on point cloud registration | |
本文首先采用体素网格重心滤波法降低点云密度,保留体积为a3的网格重心点降低点云配准计算量。其次,基于KD-Tree的点云均值滤波方法,利用该空间索引结构,将采样点的坐标值取为均值滤波窗口k邻域内各数据点的统计平均值,从而取代原有的点,平滑噪声,完成点云预处理任务。
2.2 基于法向量的点云粗配准选取降采样后点云的每一点,对其进行近邻点搜索,将包含该点的近邻点拟合成曲面,对曲面中的点进行主成分分析,查找最小特征值对应的特征向量,该特征向量即为该拟合曲面的法向量。
令θij表示点pi的法向量与其近邻点pj的法向量的夹角,定义fi为点云中某一点的法向量与其k-近邻点法向量夹角的算术平均值,以表示法向量的变化程度,表达式为
| $ f_i=\frac{1}{k} \sum\limits_{j=1}^k \theta_{i j} . $ | (1) |
求取所有点的fi均值记为ε1,保留fi>ε1的点,对于保留点中的任意一点ps,若其满足
| $ f\left(p_s\right)=\max \left[f\left(p_{s 1}\right), f\left(p_{s 2}\right), \cdots, f\left(p_{s k}\right)\right], $ | (2) |
则将ps作为特征点,其中f(ps1),f(ps2),…,f(psk)为点ps的k-近邻的特征度。设源点云为P,目标点云为Q,其中的点分别为pi和qi。根据上述方法分别对2组点云进行特征点提取,得到具有m′个P的特征点集为Pt={pt1, pt2, …, ptm′},具有n′个Q的特征点集为Qt={qt1, qt2, …, qtn′}。
对特征点集Pt和Qt建立FPFH描述子[19],依据FPFH确定特征点匹配并建立刚性不变约束,得到特征向量点集vep和veq。
在点集vep中依据特征向量之间的欧式距离为点集veq中每个点寻找最相似的点作为其匹配点,并计算误差。假设存在2组正确匹配的点对为(si1, si2)和(sj1, sj2),令点对平均距离为ε2,若满足
| $ \frac{\left|{\rm{dist}}\left(s_i^1, s_j^1\right)-{\rm{dist}}\left(s_i^2, s_j^2\right)\right|}{{\rm{dist}}\left(s_i^1, s_j^1\right)+{\rm{dist}}\left(s_i^2, s_j^2\right)}<\varepsilon_2, $ | (3) |
将点对(sj1, sj2)记为相对于点对(si1, si2)符合距离约束的点对,初始配准点集Smatch中除点对(si1, si2)外与其符合刚性距离约束的点的数目记为k。
由于初始匹配后得到的匹配点对已具备一定的精度,可通过RANSAC算法进行校验。对每个点对计算k值,按照从大到小的顺序对Smatch进行排序,选取前N个点对检验是否为正确匹配点对。
根据获得的正确匹配点集,运用四元素法计算旋转矩阵R和平移矩阵T。根据
| $ p_i^{\prime}={\boldsymbol{R}} \cdot p_i+{\boldsymbol{T}}, $ | (4) |
将源点云P中的每个点pi变换到目标点云Q坐标系下,变换后的点云记为P′,其中的点记为p′i。
2.3 基于改进ICP算法的精配准将经粗配准的点云映射到二维单元格中用概率密度函数f(p)表示,Σ表示单元格协方差矩阵。将f(p)使用Hessian矩阵法进行优化,使其达到最小值,表达式为
| $ f(p)=\sum\limits_i \exp \left[-\frac{\left(P_i^{\prime}-q_i\right)^T {\boldsymbol{\Sigma}}_i^{-1}\left(P_i^{\prime}-q_i\right)}{2}\right]. $ | (5) |
此过程可以将经过粗配准环节的点云继续进行位姿修正。接下来,通过KD-Tree查找2组点云数据的对应点并构建误差函数,采用高斯-牛顿法迭代求解误差函数E(R, T),表示为
| $ E({\boldsymbol{R}}, {\boldsymbol{T}})=\frac{1}{n} \sum\limits_{i=1}^n\left\|q_i-\left({\boldsymbol{R}} p_i^{\prime}+{\boldsymbol{T}}\right)\right\|^2. $ | (6) |
当E(R, T)满足位姿估计要求时,输出ICP精配准后的位姿变换矩阵,通过该变换矩阵可得配准后的点云,变换矩阵中的旋转矩阵对应姿态角变换,平移矩阵对应平移量。
3 实验与分析为了验证本文算法的点云配准与位姿估计性能,需要分别开展基于数字卫星的点云配准性能验证与基于卫星缩比模型的姿态估计算法验证。以配准后源点云和目标点云之间的均方误差RMSE(root mean square error,RMSE)表示配准误差,与配准时间t共同作为评价指标。RMSE是配准后的源点云P′和目标点云Q中的点距离值的平方与总点数n比值的平方根,用公式表示为
| $ {\text { RMSE }}=\sqrt{\frac{1}{n} \sum\limits_{i=1}^n\left(p_i^{\prime}-q_i\right)^2} . $ | (7) |
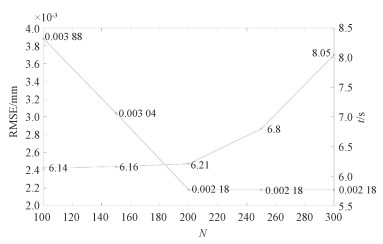
本文算法基本参数设置如表 1所示。体素网格滤波算法的边长a和近邻滤波算法的k值为滤波算法中的常见值,能在降低点云密度的同时保留点云结构。利用本文算法对斯坦福大学公开点云数据bunny000与bunny045进行配准,分析N值对RMSE和t值的影响,确定RANSAC算法的N值。参数敏感性分析实验结果如图 2所示。
|
|
表 1 基本参数设置表 Table 1 Table of basic parameter settings |
|
Download:
|
| 图 2 参数敏感性分析实验结果 Fig. 2 Parameter sensitivity analysis experiment result plot | |
选取100、150、200、250和300这5个N值进行实验,随着N值增大,RMSE呈逐渐降低并稳定的趋势,t值不断上升。在N=200时,RMSE和t值的效果最佳。因此,本文选用N=200进行实验。
3.1 基于数字卫星模型的点云配准性能验证点云配准性能验证实验按配准对象分为经旋转平移变换和高斯噪声处理的6组数字卫星点云模型2个子项。
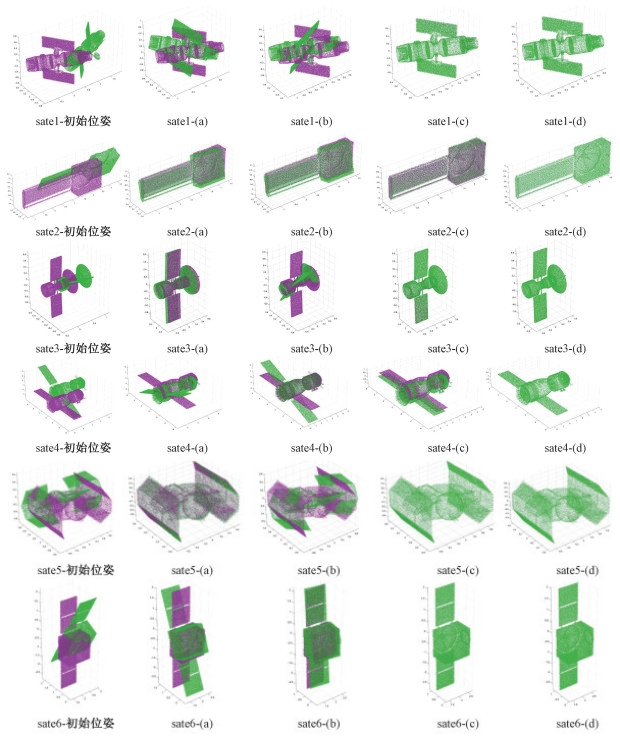
3.1.1 无噪声条件下的数字卫星点云配准验证选取6种卫星点云模型分别进行旋转平移变换,初始位姿如图 3第1列所示。分别使用ICP算法[7]、NDT-ICP算法、一种基于法向量的点云自动配准方法[11](以下简称法向量算法)和本文算法对上述点云模型进行配准。6种卫星点云模型的配准结果如图 3后4列所示,图 3(a)~3(d)分别指ICP、NDT-ICP、法向量和本文算法。由sate1得,ICP算法和NDT-ICP算法在针对具备“中心对称”特性的帆板卫星配准方面存在误差,原始卫星点云与目标卫星点云的帆板方向出现反置。相比本文算法,法向量算法在卫星上方帆板局部存在点云色差。对于sate1,本文算法配准效果最优。由单板卫星sate2得,ICP算法和NDT-ICP算法的配准误差较大;法向量算法的点云色差较为明显,重合度较差。在4种算法中,本文算法的点云色差最小,重合度最好,配准效果最优。本文算法在其他4组卫星点云模型的配准中同样表现最佳。由效果图分析得,本文算法能有效解决卫星点云配准过程中出现的帆板对齐效果不佳、点云重合度较差等问题。
|
Download:
|
| 图 3 sate1~sate6的初始位姿与不同算法的配准效果对比 Fig. 3 Comparison of the initial pose of sate1-sate6 with the registration effect of different algorithms | |
本实验的性能参考指标t与RMSE如表 2所示。由表知,本文算法RMSE的数值均为最低,配准精度最高,配准效果最为稳定。
|
|
表 2 针对不同卫星点云模型的多种算法配准结果 Table 2 Registration results of multiple algorithms for different satellite point cloud models |
考虑到实际场景的点云配准中会出现光照、拍摄视角、遮挡等因素的影响,对无噪声条件下sate1~sate6卫星点云添加σ=0.01高斯噪声,分别记为sate1′、sate2′、sate3′、sate4′、sate5′、sate6′进行配准,以验证本文算法抗干扰的能力。算法配准所需的时间t与RMSE如表 3所示。
|
|
表 3 经高斯噪声处理的卫星点云模型的多种算法配准结果 Table 3 Multiple algorithm registration results of Gaussian noise-processed satellite point cloud models |
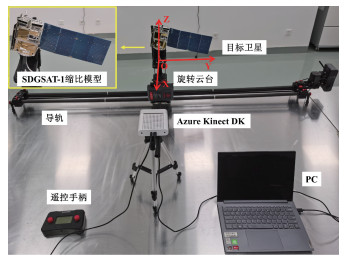
利用TOF相机Azure Kinect DK采集可持续发展科学卫星1号(SDGSAT-1)缩比模型在不同位姿条件下的点云数据并进行位姿估计,分析比较不同算法的时间与误差。实验场景如图 4所示,具备绕2轴旋转的旋转云台与导轨组成了位姿控制装置。将卫星模型固定在该系统上,定义图中卫星模型位姿为原始位姿,通过遥控手柄实现对卫星模型的旋转与平移。
|
Download:
|
| 图 4 实验场景图 Fig. 4 Experimental scene graph | |
定义世界坐标系的Y轴平行于导轨,原点位于旋转云台2旋转轴的相交处,如图 4的坐标系示意图所示。相机镜头与图 4原点O点的水平距离为0.6 m,Azure Kinect DK的深度摄像头模式为NFOV非装箱模式,视场角(水平×垂直)为75°×65°。利用棋盘格标定法求出相机外参,确定相机坐标系到世界坐标系的矩阵变换关系。
为验证本文位姿估计算法的有效性和鲁棒性,设计了5组实验,对原始位姿下的卫星模型进行变换,实验描述如表 4所示。将变换后的对象作为目标模型,将原始位姿作为参考模型分别使用ICP、NDT-ICP、法向量和本文算法进行配准。采用阈值分割法对Azure Kinect DK采集到的点云进行目标提取。其中,实验1至实验3旨在验证单轴变换条件下,本文算法的位姿估计能力;实验4旨在验证3轴变换条件下,本文算法位姿估计的鲁棒性与准确度;实验5旨在验证本文算法在遮挡条件下的位姿估计能力。
|
|
表 4 卫星缩比模型实验描述 Table 4 Satellite model scaled experiment description |
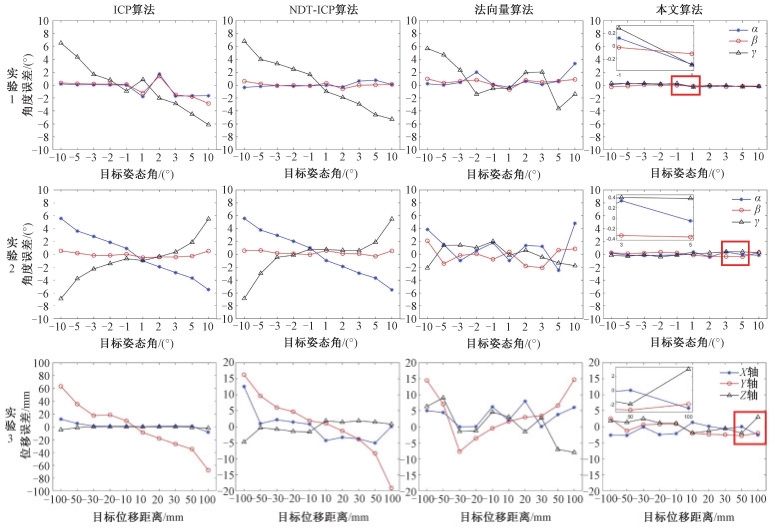
图 5为实验1至实验3条件下,姿态角与位移误差的对比折线图。由图可知,在单轴变换条件下,本文算法相较于前3种传统算法的精度最佳,鲁棒性最高。其中,姿态角误差最小不超过0.4°,平均位移误差不超过3 mm。
|
Download:
|
| 图 5 不同实验条件下4种算法姿态角与位移误差对比 Fig. 5 Comparison line chart of attitude angle and displacement error of four algorithms under different experimental conditions | |
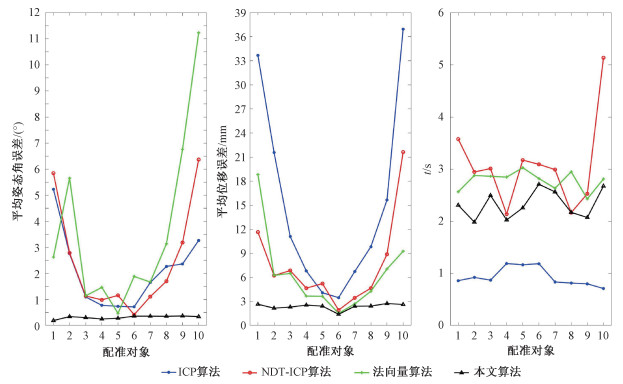
将实验4中10组配准对象分别使用ICP、NDT-ICP、法向量和本文算法进行位姿估计,将平均姿态角误差、平均位移误差与位姿估计时间t作为配准评价标准。如图 6所示,用编号代替不同的配准对象。由图可知,本文算法的配准姿态角误差稳定在0.4°以内,位移误差稳定在3 mm以内。
|
Download:
|
| 图 6 特定位姿变换下的相对位姿估计性能对比 Fig. 6 Comparison chart of registration performance under specific pose transformation | |
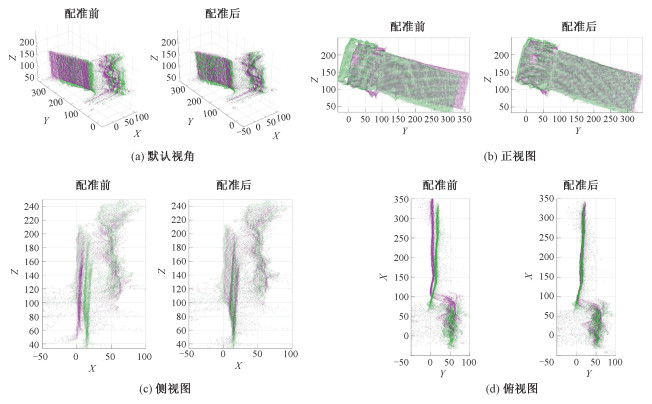
图 7是实验4的第3组配准对象,即将原始位姿卫星模型绕X轴旋转-3°,沿Y轴平移-30 mm并绕Z轴旋转-3°采集到的点云和原始位姿点云经本文位姿估计算法产生的配准结果图。由点云色差得,本文算法对点云进行配准的效果较好,重合度较高。
|
Download:
|
| 图 7 第3组配准对象的配准结果 Fig. 7 The registration effect images of the third group of registration objects | |
在配准时间方面,本文算法虽大于ICP算法的配准时间,但由于ICP算法容易陷入局部最优而导致匹配不准确,鲁棒性差、配准精度低,而本文算法的配准精度、鲁棒性在对比中均表现最佳,且配准时间小于NDT-ICP算法和法向量算法。综上,本文算法的配准性能最好,效果最优。
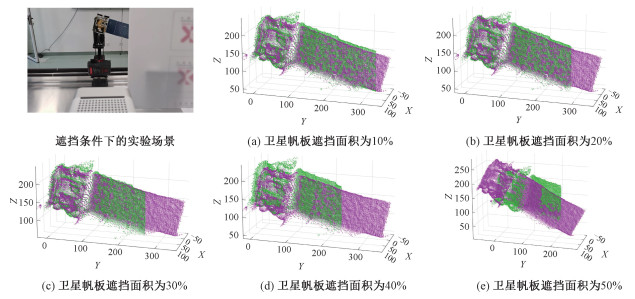
3.2.3 遮挡条件下的位姿估计算法验证为验证本文算法在遮挡条件下的位姿估计性能,将原始位姿卫星模型绕X轴旋转1°,绕Z轴旋转1°,沿Y轴平移10 mm,用光滑平整的塑料板对卫星模型的帆板进行遮挡,实验场景如图 8的第1幅图所示。水平移动塑料板,利用相机提取不同遮挡条件下的模型点云,与原始位姿卫星模型点云进行配准,验证本文算法在不同遮挡条件下的位姿估计性能,选取具有代表性的配准结果进行分析,如图 8(a)~8(e)所示。
|
Download:
|
| 图 8 遮挡条件下的实验场景与实验结果 Fig. 8 Experimental scene and experimental result plots under occlusion conditions | |
由图可知,当卫星帆板遮挡面积为30 % 以内时,本文算法具备较好的配准效果;遮挡面积为40 % 时,卫星点云的重合度产生较大偏差;遮挡面积为50 % 时,本文算法配准失败。图 8(a)~8(e)5种遮挡条件下的位姿估计误差如表 5所示。实验表明,对卫星帆板的遮挡面积在30 % 以内时,本文算法具备较好的位姿估计性能。
|
|
表 5 不同遮挡条件下的位姿估计误差 Table 5 Attitude estimation error under different occlusion conditions |
本文实验的硬件环境为AMD Ryzen 7 5800HS Creator Edition 3.20 GHz处理器,16.0 GB内存。经测试,本文提出算法的CPU平均占用率约为9.7 %,利用C++语言运行程序的内存需求约为16 MB。实验4的算法平均总运算时长为2.126 s,实验5的平均总运算时长为1.864 s。上述算法总运行时长由点云预处理和点云配准两部分组成。点云预处理可调用星载计算机空闲时间完成,本文点云预处理平均运行时间约为1.6 s,则位姿估计时间节省至0.395 s左右。按照CPU频率关系进行换算,在100 MHz的星上处理条件下,本文算法位姿估计时间约为12.94 s。
4 结论本文以解决空间非合作目标位姿估计问题为目的,以点云配准为导向,提出一种基于点云配准的空间非合作目标位姿估计算法。实现了对数字卫星点云模型的配准性能验证,并对TOF相机采集的卫星缩比模型点云进行位姿估计算法验证。
1) 在数字卫星仿真实验中,对6种模型进行配准实验验证,并在此基础上添加高斯噪声以验证本文算法的稳定性。结果表明:本文算法在卫星点云模型的配准方面能够有效解决配准过程中出现的帆板对齐效果不佳、点云重合度较差等问题。
2) 在卫星缩比模型实验中,通过位姿控制装置对卫星模型进行位姿变换,使用TOF相机对SDGSAT-1缩比模型采集若干组点云数据,利用本文算法进行位姿估计。结果表明:本文算法优于其他典型配准算法,姿态角测量误差小于0.4°,位移测量误差小于3 mm,具备良好的配准效果。遮挡实验表明,对卫星帆板的遮挡面积在30 % 以内时,本文算法具备较好的位姿估计性能。
今后,考虑通过在轨验证对本文算法进行进一步测试与优化。
| [1] |
Meng G, Han L L, Zhang C F. Research progress and technical challenges of space robot[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(1): 1-27. Doi:10.7527/S1000-6893.2020.23963 |
| [2] |
Brannan J, Scott N, Carignan C. Robot servicer interaction with a satellite during capture[C/OL]//International Symposium on Artificial Inte-lligence, Robotics and Automation in Space (iSAIRAS). (2018-07-12)[2022-12-21]. https://robotics.estec.esa.int/i-SAIRAS/isairas2018/Papers/Session%203b/1_brancarscott18_iSAIRAS_SUBMITTED_TO_SSPD-18-49-Brannan-Justin.pdf.
|
| [3] |
程瑞洲, 黄攀峰, 刘正雄, 等. 一种面向在轨服务的空间遥操作人机交互方法[J]. 宇航学报, 2021, 42(9): 1187-1196. Doi:10.3873/j.issn.1000-1328.2021.09.014 |
| [4] |
Peng J Q, Xu W F, Liang B, et al. Pose measurement and motion estimation of space non-cooperative targets based on laser radar and stereo-vision fusion[J]. IEEE Sensors Journal, 2019, 19(8): 3008-3019. Doi:10.1109/JSEN.2018.2889469 |
| [5] |
刘王超, 娄鑫. 基于双目点云的三维物体检测准确性分析[J]. 中国科学院大学学报, 2022, 39(5): 677-683. Doi:10.7523/j.ucas.2020.0042 |
| [6] |
陈凤, 朱洁, 顾冬晴, 等. 基于激光成像雷达的空间非合作目标相对导航技术[J]. 红外与激光工程, 2016, 45(10): 107-114. Doi:10.3788/IRLA201645.1030005 |
| [7] |
Besl P J, McKay N D. Method for registration of 3-D shapes[C]//Proc SPIE 1611, Sensor Fusion Ⅳ: Control Paradigms and Data Structures, 1992, 1611: 586-606. DOI: 10.1117/12.57955.
|
| [8] |
唐思琦, 韩丛英, 郭田德. 基于机器学习的点集匹配算法[J]. 中国科学院大学学报, 2020, 37(4): 450-457. Doi:10.7523/j.issn.2095-6134.2020.04.003 |
| [9] |
王飞鹏, 肖俊, 王颖, 等. 一种基于高斯曲率的ICP改进算法[J]. 中国科学院大学学报, 2019, 36(5): 702-708. Doi:10.7523/j.issn.2095-6134.2019.05.016 |
| [10] |
周颖, 林意. 基于法向量投票的点云配准方法[J]. 计算机应用研究, 2022, 39(2): 637-640. Doi:10.19734/j.issn.1001-3695.2021.06.0236 |
| [11] |
陶海跻, 达飞鹏. 一种基于法向量的点云自动配准方法[J]. 中国激光, 2013, 40(8): 184-189. Doi:10.3788/CJL201340.0809001 |
| [12] |
韩一菲, 杨紫骞, 郑福, 等. 基于FPFH和法向量的改进点云配准算法[J]. 半导体光电, 2021, 42(4): 579-584. Doi:10.16818/j.issn1001-5868.2021.04.025 |
| [13] |
石峰源, 郑循江, 姜丽辉, 等. 基于霍夫变换的空间非合作目标点云配准算法[J]. 北京航空航天大学学报, 2023, 49(8): 2071-2078. Doi:10.13700/j.bh.1001-5965.2021.0575 |
| [14] |
卢祺, 林婷婷, 李程鹏, 等. 空间非合作目标点云聚类配准方法[J]. 红外与激光工程, 2021, 50(9): 362-371. Doi:10.3788/IRLA20200431 |
| [15] |
Ding Q Y, He J. The detection of non-cooperative targets in space by using 3D point cloud[C]//2019 5th international Conference on Control, Automation and Robotics (ICCAR). April 19-22, 2019, Beijing, China. IEEE, 2019: 545-549. DOI: 10.1109/ICCAR.2019.8813367.
|
| [16] |
Bentley J L. Multidimensional binary search trees used for associative searching[J]. Communications of the ACM, 1975, 18(9): 509-517. Doi:10.1145/361002.361007 |
| [17] |
Weber T, Hänsch R, Hellwich O. Automatic registration of unordered point clouds acquired by Kinect sensors using an overlap heuristic[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2015, 102: 96-109. Doi:10.1016/j.isprsjprs.2014.12.014 |
| [18] |
Huang P Z, Yang Y B, Huang T C. Real-time measurement of model attitude based on NDT and ICP[C]//4th Optics Young Scientist Summit (OYSS 2020). December 4-7, 2020. Ningbo, China. SPIE, 2021, 11781: 302-308. DOI: 10.1117/12.2591140.
|
| [19] |
Lin S D, Peng Y P, Cao G Z. Low overlapping plant point cloud registration and splicing method based on FPFH[C]//Chinese Conference on Image and Graphics Technologies. Singapore: Springer, 2022: 103-117. DOI: 10.1007/978-981-19-5096-4_8.
|
 2024, Vol. 41
2024, Vol. 41 


