高功率飞秒脉冲在空气中传输时,由于衍射、克尔自聚焦和电子散焦的共同作用会产生高光强的细丝,并保持一定的束宽传输较长距离,传输距离远远超过瑞利长度,这个过程被称为飞秒激光成丝。在飞秒激光成丝过程中伴有高次谐波[1-2]、超连续辐射[3-4]和强度钳制[5-6]等丰富的非线性现象。基于这些特性,飞秒激光成丝能够用于遥感探测[7-9]、诱导闪电[10-12]、驱散云雾[13-14]以及激光诱导击穿光谱探测等应用[15-16]。这些远距离应用对飞秒激光成丝提出了各种各样的需求,这些都需要深入理解成丝过程并根据应用对飞秒激光成丝的特性进行控制和优化,如控制成丝起点、成丝长度、强度以及成丝模式分布等。其中一个关键问题就是如何延长飞秒激光成丝的长度。迄今为止,人们已经提出多种延长脉冲成丝的方法,比如加入微透镜阵列[17-18]、声光调制[19]、脉冲整形[20-22]和改变聚焦条件[23-25]等。除此以外,改变初始脉冲空间分布,比如使用贝塞尔光束[26-27]也可以有效延长成丝长度。近几年,由于涡旋光束具有环形强度和螺旋相位的特殊空间分布,飞秒涡旋光的成丝受到广泛关注[28-30]。飞秒涡旋光在空气中有更高的自聚焦临界功率,能够携带更高的能量在更远的位置上成丝[31-32],但如何延长飞秒涡旋光成丝过程仍未见报道。
飞秒涡旋光由于调制不稳性,其涡旋环会劈裂塌缩成多丝,在这之前,在自聚焦的作用下,涡旋环直径会逐渐减小直至在百微米量级[33]。这样的光强分布与飞秒激光成丝后产生的空气密度孔的尺寸较为匹配[34],由此,本文提出在飞秒涡旋光的传输路径上引入空气密度孔,对飞秒涡旋光的成丝过程进行控制,以实现飞秒涡旋光成丝长度的延长。空气密度孔是飞秒激光成丝后空气热扩散所产生的柱状结构,光轴上的空气密度比周围低,相应的折射率分布类似于反波导的分布,因此也可以称之为反波导结构,其直径在百微米量级[34]。在我们之前的工作中,对飞秒高斯光产生单丝的过程引入空气密度孔[35],其中心正对单丝的光强峰值位置,密度孔的散焦以及飞秒高斯光的自聚焦和电子散焦之间建立的新平衡有效延长了单丝的长度。然而,涡旋光的强度分布是环形的,成丝后细丝会绕光轴旋转传输[32, 36],我们引入的密度孔中心正对涡旋环中心的相位奇点,密度孔的散焦将引起涡旋环传输过程的改变,从而改变涡旋环上的成丝过程,这与飞秒高斯光的情况有极大的不同。
本文理论模拟了不同能量的飞秒涡旋光在空气中的成丝过程,在飞秒涡旋光的传输过程中引入密度孔,密度孔的中心与涡旋光的奇点位置重合。通过改变密度孔的纵向位置和长度,极大延长了飞秒涡旋光的成丝过程。通过进一步的理论分析发现,由于引入的密度孔对涡旋环具有散焦作用,改变了脉冲后沿的再聚焦过程,进而有效地延长了飞秒涡旋光成丝过程。
1 计算飞秒涡旋脉冲在空气中的传输可以用非线性薛定谔方程耦合电子产生方程[37]来描述:
| $ \frac{\partial E}{\partial z}={\mathrm{i}} \frac{1}{2 k_0} \Delta_{\perp} E-{\mathrm{i}} \frac{k^{\prime \prime}}{2} \frac{\partial^2 E}{\partial t^2}+{\mathrm{i}} \frac{k_0 n_2}{2} R(t) E-\\{\mathrm{i}} k_0 \frac{\rho}{2 \rho_{{\mathrm{c}}}} E-\frac{\beta^{(K)}}{2}|E|^{2 K-2} E+{\mathrm{i}} k_0 \Delta n E, $ | (1) |
| $ \frac{\partial \rho}{\partial t}=\frac{\beta^{(K)}}{K \hbar \omega_0}|E|^{2 K}\left(1-\frac{\rho}{\rho_{{\mathrm{at}}}}\right) , $ | (2) |
| $ R(t)=|E|^2+\frac{1}{\tau_k}\left(\int\limits_{-\infty}^t {\mathrm{e}}^{-\frac{t-t^{\prime}}{\tau_k}}\left|E\left(t^{\prime}\right)\right|^2 {\mathrm{~d}} t^{\prime}\right) . $ | (3) |
式(1)右侧分别是衍射、群速度色散、克尔效应、电子散焦、多光子吸收和密度孔引起的折射率变化。E为电场包络,z为传输距离,k0为激光中心波长(λ0=800 nm)对应的波数,ρ为电子密度。Δn为预脉冲成丝产生的密度孔引起的折射率变化。通过整步傅里叶变换和半隐式差分方法求解以上耦合方程组。数值模拟所用参数如表 1所示。横截面、传输距离以及时间上的计算步长分别为0.03 mm,1.25 mm和0.7 fs。
|
|
表 1 模拟参数选值 Table 1 Simulation parameters |
计算的初始飞秒涡旋脉冲电场包络写为
| $ E=E_0 \frac{r}{w} {\mathrm{e}}^{-\frac{r^2}{2 w^2}} {\mathrm{e}}^{-\frac{t^2}{0.72 \tau^2}} {\mathrm{e}}^{-\frac{{\mathrm{i}} k_0 r^2}{2 f}} {\mathrm{e}}^{{\mathrm{i}} m \varphi}, $ | (4) |
其中: 脉冲脉宽τ=30 fs,半径为w=1 mm,透镜焦距f=2 m,φ为方位角,拓扑电荷m=1。密度孔引起的折射率变化[38]为
| $ \Delta n=\Delta n_m {\mathrm{e}}^{-\frac{x^2+y^2}{R^2}}. $ | (5) |
该密度孔由预先传输的飞秒高斯脉冲成丝产生,其半径R和中心处折射率变化Δnm都随时间变化[38],具体公式为
| $ R=\sqrt{R_0^2+4 \alpha \Delta t}, $ | (6) |
| $ \Delta n_m=\left(1-n_0\right) \frac{\Delta T_{\text {peak }}}{T_{\mathrm{a}}} \frac{R_0^2}{R^2}. $ | (7) |
其中:空气温度Ta=300 K,折射率n0=1.000 275,热扩散速率α=0.19 cm2/s,温度变化峰值ΔTpeak= 50 K[38],密度孔初始半径R0=50 μm[34]。计算当密度孔的产生与后续传输的飞秒涡旋光之间的时间间隔Δt分别为0.5、1.0、1.5、2.0和4.0 ms,对应的密度孔半径和折射率变化峰值分别为,R=0.20、0.28、0.34、0.39、0.55 mm,Δnm=-2.83×10-6、-1.46×10-6、-9.84×10-7、-7.42×10-7、-3.74×10-7。
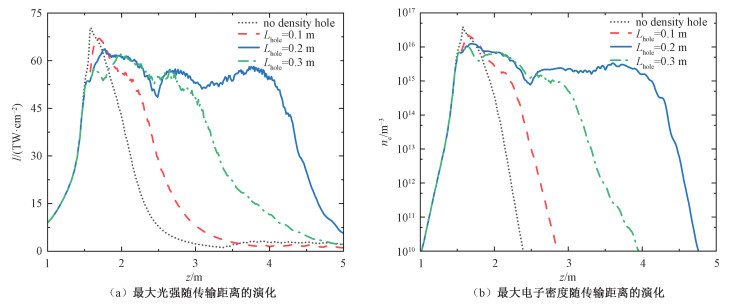
2 结果和分析图 1为未加密度孔和加入不同长度的密度孔后(Δt=1 ms),能量为4 mJ的飞秒涡旋脉冲最大光强和产生的最大电子密度随传输距离的演化。密度孔的产生与飞秒涡旋光之间的时间间隔为1 ms,其起始点均为1.4 m,长度分别为0.1 m(红虚线)、0.2 m(蓝实线)和0.3 m(绿虚点线),黑点线代表无密度孔。从图中可以看到,未加密度孔时,飞秒涡旋脉冲在z=1.43 m处开始成丝,到z=2.07m处结束,成丝长度为0.64 m,峰值光强最大可达70 TW/cm2,其中,成丝起点和终点均定义为最大光强值一半的位置。当在成丝起始位置(z=1.4 m)加入密度孔后,飞秒涡旋光的成丝得到了显著延长。密度孔的长度分别是0.1, 0.2, 0.3 m时,成丝长度分别为0.99, 2.92, 1.80 m,其中加入0.2 m的密度孔时,成丝长度的延长最大,为无密度孔时成丝长度的4.5倍。另一方面,加入密度孔后,最大光强略小于无密度孔时的情况,这也减小了电离消耗的能量,有利于成丝的延长。
|
Download:
|
| 图 1 4 mJ飞秒涡旋脉冲在不同长度密度孔的空气中传输时,最大光强和电子密度随传输距离的演化 Fig. 1 Evolution of peak intensity and electron density of the 4 mJ femtosecond vortex beam in air as a function of propagation distance for different length density holes | |
为了更深入地理解加入密度孔后飞秒涡旋光成丝延长的物理机制,给出有无密度孔情况下光强的时空分布,如图 2所示。从图 2(a)和2(b)可以看出,未加密度孔时,涡旋脉冲中心峰值部分首先聚焦成丝(z=1.6 m),此时涡旋环最大光强处半径约为0.08 mm,电离产生了密度为2.87×1016 cm-3的电子。如此分布的电子对脉冲后沿的涡旋环有明显的散焦。到了z=2.0 m,脉冲前沿聚焦成丝,被散焦的后沿圆环强度很低,光强低于5 TW/cm2。随着传输距离的增加,脉冲后沿的涡旋环没有再聚焦,无法成丝。并且,由图 2(b)可以看出,没有加密度孔时,成丝呈环状分布,脉冲在传输过程中会损耗更多的能量。从图 2(c)和2(d)看出,加入密度孔(1.4~1.6 m)后,也是脉冲中心峰值部分先聚焦成丝,由于引入的密度孔对涡旋环的散焦作用,聚焦后的涡旋环最大光强处半径约为0.16 mm,比无密度孔的情况要大得多。密度孔的散焦作用还引起涡旋环角向调制不稳性的增加,脉冲中心部分涡旋环劈裂成多丝,由此产生的电子密度虽然可达到1.24×1016 cm-3,但半径较大且离散分布的电子对后沿圆环虽有散焦作用,并没有抑制脉冲后沿的再聚焦。随着传输距离的增加,脉冲后沿再聚焦,形成一根单丝,从而导致涡旋光成丝被极大地延长,这将更有利于遥感探测和激光诱导击穿光谱探测等应用。但由于角向调制不稳性的增加使得涡旋光成丝不再是环形分布,这限制了如环形波导这样需要较高空间对称性的应用。

|
Download:
|
| 图 2 4 mJ飞秒涡旋脉冲在不同传输位置光强的时空分布 Fig. 2 Temporal and spatial distribution of 4 mJ femtosecond vortex beam intensity at different propagation distances | |
其他长度的密度孔对涡旋光成丝均有不同程度的影响,具体分析如下。当加入0.1 m的密度孔时,涡旋光成丝只比无密度孔时稍有延长。这是因为,密度孔对涡旋环的散焦较弱,脉冲中心部分涡旋环自聚焦时产生的电子分布相对无密度孔时,半径稍有增大密度稍有降低,对脉冲后沿的再聚焦仍有比较强的抑制作用,因此比无密度孔时成丝略有延长。当加入0.3 m密度孔时,涡旋光成丝比无密度孔时延长很多,但较于0.2 m密度孔的情况反而减小。飞秒涡旋脉冲峰值部分圆环聚焦时,涡旋环成丝半径大于无密度孔的情况,电子密度也只有无密度孔的1/4。在这样的电子分布条件下,脉冲后沿能够再聚焦。因此,加入0.3 m的密度孔后,飞秒涡旋光成丝比无密度孔时延长很多。但是由于密度孔更强的散焦作用,在之后的传输过程中,脉冲后沿虽然能够再聚起来,但强度有所降低,所以这时的成丝长度要比加入0.2 m密度孔的情况短很多。
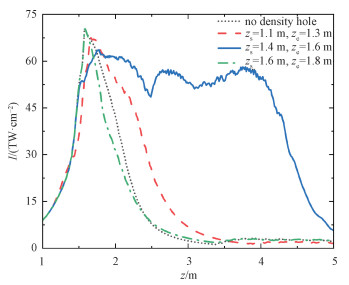
我们还研究了从不同初始位置引入密度孔后,飞秒涡旋光成丝的演化,结果如图 3所示。黑点线代表无密度孔,红虚线、蓝实线和绿虚点线分别代表在1.1~1.3、1.4~1.6和1.6~1.8 m引入密度孔。当密度孔的始末位置分别为zs=1.1 m,ze=1.3 m时,此时的密度孔位于涡旋光成丝前自聚焦的初始阶段,涡旋环半径较大,光强比较低,密度孔对涡旋环的散焦作用仅仅是延缓了飞秒涡旋脉冲的聚焦过程,对涡旋环成丝后产生电子的分布影响很小,因此密度孔的散焦作用没有明显改变后沿涡旋环的再聚焦过程。所以这种情况下,密度孔的作用表现为成丝起点的推迟,成丝长度略有延长。当密度孔的始末位置分别为zs=1.6 m,ze=1.8 m时,此区间的光强已在达到最大值后开始降低,密度孔的散焦与脉冲峰值部分产生的电子散焦共同作用,脉冲后沿的涡旋环被强烈散焦,光强降低得更快,成丝长度反而不如无密度孔的情况。只有密度孔的起始位置属于自聚焦过程中光强迅速增加至最大光强的这个阶段,即成丝起点位置附近,其对涡旋环的散焦作用才刚刚好减弱脉冲峰值部分涡旋环产生的电子对后沿圆环的散焦作用,有利于脉冲后沿的再聚焦,能够明显延长涡旋光的成丝过程。
|
Download:
|
| 图 3 4 mJ飞秒涡旋脉冲在不同位置的密度孔的空气中传输时,最大光强随传输距离的演化 Fig. 3 Evolution of peak intensity of the 4 mJ femtosecond vortex beam in air as a function of propagation distance for density holes at different positions | |
在实际实验中,改变时间延迟比改变密度孔的空间位置和长度更容易实现。所以,我们还研究了当密度孔的纵向位置固定为1.4~1.6 m时,改变密度孔和涡旋光之间的时间延迟时,涡旋光的成丝传输,如图 4所示。黑实线代表无密度孔,红虚线、蓝点线、绿虚点线和紫短虚线分别代表密度孔的时间延迟为0.5、1.0、1.5和2.0 ms,纵向位置为1.4~1.6 m。时间延迟为1.0 ms时,延长效果是最好的。当时间延迟为0.5 ms时,密度孔的折射率较高,对涡旋环有很强的散焦作用,光强在这段距离里快速下降,之后由于后沿再聚焦光强再次增大,成丝有较好的延长。时间延迟为1.5和2.0 ms时,密度孔对脉冲的散焦作用比较弱,因此成丝长度略有延长。

|
Download:
|
| 图 4 4 mJ飞秒涡旋脉冲在不同时间延迟的密度孔的空气中传输时,最大光强随传输距离的演化 Fig. 4 Evolution of peak intensity of the 4 mJ femtosecond vortex beam in air as a function of propagation distance for density holes with different time delays | |
我们还研究了具有较高能量的飞秒涡旋脉冲的成丝传输过程。图 5为8 mJ的涡旋脉冲在加入相同长度、不同初始位置的密度孔后激光脉冲最大光强和最大电子密度随传输距离的演化。黑实线代表无密度孔,红虚线、蓝点线、绿虚点线和紫短虚线分别代表在传输距离为0.7~1.1、0.8~1.2、0.9~1.3和1.0~1.4 m引入密度孔。在未加密度孔时,成丝起始于1.02 m, 终止于2.04 m, 长度为1.02 m,峰值光强最大可达80 TW/cm2,脉冲中心部分的涡旋环聚焦时半径约为0.05 mm,电子密度达到8.52×1016 cm-3。如此分布的电子密度对脉冲后沿圆环有很强的散焦作用,脉冲后沿始终无法再聚焦直至成丝结束。与上述4 mJ飞秒涡旋脉冲传输情况类似,当密度孔位于涡旋光自聚焦的初始阶段时(始末位置分别为zs=0.7 m,ze=1.1 m),密度孔的散焦作用对脉冲中心圆环产生的电子分布影响不大,所以脉冲后沿也无法再聚焦,但此时脉冲中心部分产生的最大电子密度较无密度孔时有所降低,电离耗散减小,因此成丝长度略有延长,为1.18 m。当密度孔的始末位置处于自聚焦阶段光强比较大的区域时,即成丝起点区域(如zs=0.8 m,ze=1.2 m或zs=0.9 m,ze=1.3 m),密度孔对脉冲中心圆环的散焦作用使得环上最大电子密度降低,减弱了对脉冲后沿圆环的散焦,脉冲后沿能够逐渐聚起来重新成丝,成丝比无密度孔时明显延长。当密度孔的始末位置为zs=1.0 m,ze=1.4 m时,这个范围内的光强较于前3种情况要更强,密度孔会与脉冲中心部分产生的电子散焦共同作用,对脉冲后沿圆环的散焦作用更强,使得脉冲后沿在z=2.4 m附近没有聚起来,成丝长度为1.43 m。因此,对于较高能量的飞秒涡旋光,在自聚焦光强比较大的阶段加入密度孔同样能够延长成丝,并且需要更长的密度孔。

|
Download:
|
| 图 5 8 mJ飞秒涡旋脉冲在不同位置的密度孔的空气中传输时,最大光强和电子密度随传输距离的演化 Fig. 5 Evolution of peak intensity and electron density of the 8 mJ femtosecond vortex beam in air as a function of propagation distance for density holes at different positions | |
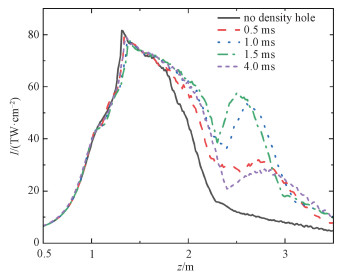
对于较高能量的飞秒涡旋脉冲的成丝传输,我们也研究了密度孔和涡旋光之间的时间延迟对成丝的影响。如图 6所示,黑实线代表无密度孔,红虚线、蓝点线、绿虚点线和紫短虚线分别代表密度孔的时间延迟为0.5、1.0、1.5和4.0 ms,纵向位置为0.8~1.2 m。密度孔的纵向位置固定为0.8~1.2 m,不同时间延迟的密度孔对成丝早期阶段影响差别不大。时间延迟为0.5 ms时,密度孔的散焦作用使得脉冲后沿没有再聚焦的过程,无法延长成丝。时间延迟为4.0 ms时,密度孔的散焦作用很弱,对涡旋光成丝过程影响很小。当时间延迟为1.0和1.5 ms时,密度孔对涡旋环的散焦作用有利于脉冲后沿的再聚焦过程,成丝延长效果较好。
|
Download:
|
| 图 6 8 mJ飞秒涡旋脉冲在不同时间延迟的密度孔的空气中传输时,最大光强随传输距离的演化 Fig. 6 Evolution of peak intensity of the 8 mJ femtosecond vortex beam in air as a function of propagation distance for density holes with different time delays | |
本文数值模拟了4和8 mJ的飞秒涡旋光在空气密度孔中的传输,分析其成丝延长的物理机制。结果表明,对于4 mJ的情况,在脉冲开始成丝到最大光强的范围内加入密度孔,能够显著延长成丝长度,最大可延长为无密度孔的4.5倍,其原因是密度孔的散焦作用增大了脉冲中心部分涡旋环聚焦时的半径,同时降低了电子密度,削弱了电子的产生对脉冲后沿的散焦,脉冲后沿能够重新聚焦成丝。对于8 mJ的情况,在合适的位置加入密度孔,能延长近1倍的成丝长度,但是由于脉冲能量更高,需要更长的密度孔对脉冲中心涡旋环进行适当散焦。同时,我们也考虑了不同时间延迟的密度孔对成丝延长的影响,对于4和8 mJ的情况,1.0 ms的时间延迟都是最有利于成丝延长。空气密度孔的引入使得成丝长度延长,这将更有利于遥感探测和激光诱导击穿光谱探测等远距离应用。但空气密度孔的引入也增加了调制不稳定性,使得涡旋光成丝不再是环形分布,破坏了原有的对称性,这限制了如环形波导这样需要较高空间对称性的应用。
| [1] |
Zhang C M, Wang J L, Chen X W, et al. Tunable ultraviolet source from fifth and seventh harmonic generated by mid-infrared pulses filamentation in air[J]. Laser Physics, 2009, 19(8): 1793-1795. Doi:10.1134/S1054660X09150493 |
| [2] |
Mitrofanov A V, Voronin A A, Mitryukovskiy S I, et al. Mid-infrared-to-mid-ultraviolet supercontinuum enhanced by third-to-fifteenth odd harmonics[J]. Optics Letters, 2015, 40(9): 2068-2071. Doi:10.1364/OL.40.002068 |
| [3] |
Petit Y, Henin S, Nakaema W M, et al. 1-J white-light continuum from 100-TW laser pulses[J]. Physical Review A, 2011, 83: 013805. Doi:10.1103/PhysRevA.83.013805 |
| [4] |
Lu C H, Tsou Y J, Chen H Y, et al. Generation of intense supercontinuum in condensed media[J]. Optica, 2014, 1(6): 400-406. Doi:10.1364/OPTICA.1.000400 |
| [5] |
Xu S, Zheng Y, Liu Y, et al. Intensity clamping during dual-beam interference[J]. Laser Physics, 2010, 20(11): 1968-1972. Doi:10.1134/S1054660X10210139 |
| [6] |
Heins A, Guo C L. Spectral investigation of higher-order Kerr effects in a tight-focusing geometry[J]. Optics Express, 2013, 21(24): 29401-29411. Doi:10.1364/OE.21.029401 |
| [7] |
Kasparian J, Rodriguez M, Méjean G, et al. White-light filaments for atmospheric analysis[J]. Science, 2003, 301(5629): 61-64. Doi:10.1126/science.1085020 |
| [8] |
Xu H L, Daigle J F, Luo Q, et al. Femtosecond laser-induced nonlinear spectroscopy for remote sensing of methane[J]. Applied Physics B, 2006, 82(4): 655-658. Doi:10.1007/s00340-005-2123-8 |
| [9] |
Chin S L, Xu H L, Luo Q, et al. Filamentation "remote" sensing of chemical and biological agents/pollutants using only one femtosecond laser source[J]. Applied Physics B, 2009, 95(1): 1-12. Doi:10.1007/s00340-009-3381-7 |
| [10] |
Wolf J P. Short-pulse lasers for weather control[J]. Reports on Progress in Physics, 2018, 81(2): 026001. Doi:10.1088/1361-6633/aa8488 |
| [11] |
Produit T, Walch P, Herkommer C, et al. The laser lightning rod project[J]. European Physical Journal-applied Physics, 2021, 93(1): 10504. Doi:10.1051/epjap/2020200243 |
| [12] |
Herkommer C, Krötz P, Jung R, et al. Ultrafast thin-disk multipass amplifier with 720 mJ operating at kilohertz repetition rate for applications in atmospheric research[J]. Optics Express, 2020, 28(20): 30164-30173. Doi:10.1364/OE.404185 |
| [13] |
Schimmel G, Produit T, Mongin D, et al. Free space laser telecommunication through fog[J]. Optica, 2018, 5(10): 1338-1341. Doi:10.1364/OPTICA.5.001338 |
| [14] |
Schroeder M C, Larkin I, Produit T, et al. Molecular quantum wakes for clearing fog[J]. Optics Express, 2020, 28(8): 11463-11471. Doi:10.1364/OE.389393 |
| [15] |
Kotzagianni M, Couris S. Femtosecond laser induced breakdown for combustion diagnostics[J]. Applied Physics Letters, 2012, 100(26): 264104. Doi:10.1063/1.4731781 |
| [16] |
Baudelet M, Guyon L, Yu J, et al. Spectral signature of native CN bonds for bacterium detection and identification using femtosecond laser-induced breakdown spectroscopy[J]. Applied Physics Letters, 2006, 88(6): 063901. Doi:10.1063/1.2170437 |
| [17] |
Xi T T, Zhao Z J, Hao Z Q. Femtosecond laser filamentation with a microlens array in air[J]. Journal of the Optical Society of America B, 2015, 32(1): 163-166. Doi:10.1364/JOSAB.32.000163 |
| [18] |
Camino A, Hao Z Q, Liu X, et al. Control of laser filamentation in fused silica by a periodic microlens array[J]. Optics Express, 2013, 21(7): 7908-7915. Doi:10.1364/OE.21.007908 |
| [19] |
Hu Y Z, Nie J S, Sun K, et al. Generation of periodic filament arrays in air through two-dimensional acousto-optic modulation[J]. Journal of the Optical Society of America B, 2016, 33(10): 2144-2148. Doi:10.1364/JOSAB.33.002144 |
| [20] |
Chen A M, Li S Y, Qi H X, et al. Elongation of plasma channel generated by temporally shaped femtosecond laser pulse[J]. Optics Communications, 2017, 383: 144-147. Doi:10.1016/j.optcom.2016.08.079 |
| [21] |
Zhan L D, Xu M N, Xi T T, et al. Contributions of leading and tailing pulse edges to filamentation and supercontinuum generation of femtosecond pulses in air[J]. Physics of Plasmas, 2018, 25(10): 103102. Doi:10.1063/1.5045783 |
| [22] |
Li J, Tan W J, Si J H, et al. Control of the spatial characteristics of femtosecond laser filamentation in glass via feedback-based wavefront shaping with an annular phase mask[J]. Optics Express, 2021, 29(4): 5972-5981. Doi:10.1364/OE.418334 |
| [23] |
Geints Y E, Zemlyanov A A. Effect of high-power laser divergence on the plasma structural parameters during multiple filamentation in air[J]. Physical Review A, 2016, 93(6): 063833. Doi:10.1103/PhysRevA.93.063833 |
| [24] |
Hong Z F, Zhang Q B, Ali Rezvani S, et al. Extending plasma channel of filamentation with a multi-focal-length beam[J]. Optics Express, 2016, 24(4): 4029-4041. Doi:10.1364/oe.24.004029 |
| [25] |
Feng Z F, Li W, Yu C X, et al. Influence of the external focusing and the pulse parameters on the propagation of femtosecond annular Gaussian filaments in air[J]. Optics Express, 2016, 24(6): 6381-6390. Doi:10.1364/OE.24.006381 |
| [26] |
Polynkin P, Kolesik M, Roberts A, et al. Generation of extended plasma channels in air using femtosecond Bessel beams[J]. Optics Express, 2008, 16(20): 15733-15740. Doi:10.1364/OE.16.015733 |
| [27] |
Akturk S, Zhou B, Franco M, et al. Generation of long plasma channels in air by focusing ultrashort laser pulses with an axicon[J]. Optics Communications, 2009, 282(1): 129-134. Doi:10.1016/j.optcom.2008.09.048 |
| [28] |
Ju L B, Huang T W, Xiao K D, et al. Controlling multiple filaments by relativistic optical vortex beams in plasmas[J]. Physical Review E, 2016, 94(3): 033202. Doi:10.1103/PhysRevE.94.033202 |
| [29] |
Porras M A, Carvalho M, Leblond H, et al. Stabilization of vortex beams in Kerr media by nonlinear absorption[J]. Physical Review A, 2016, 94(5): 053810. Doi:10.1103/PhysRevA.94.053810 |
| [30] |
Xu L T, Li D W, Chang J W, et al. Helical filaments array generated by femtosecond vortex beams with lens array in air[J]. Results in Physics, 2021, 26: 104334. Doi:10.1016/j.rinp.2021.104334 |
| [31] |
Fibich G, Gavish N. Critical power of collapsing vortices[J]. Physical Review A, 2008, 77(4): 045803. Doi:10.1103/PhysRevA.77.045803 |
| [32] |
Polynkin P, Ament C, Moloney J V. Self-focusing of ultraintense femtosecond optical vortices in air[J]. Physical Review Letters, 2013, 111(2): 023901. Doi:10.1103/PhysRevLett.111.023901 |
| [33] |
Rozas D, Law C T, Swartzlander G A. Propagation dynamics of optical vortices[J]. Journal of the Optical Society of America B, 1997, 14(11): 3054-3065. Doi:10.1364/JOSAB.14.003054 |
| [34] |
Cheng Y H, Wahlstrand J K, Jhajj N, et al. The effect of long timescale gas dynamics on femtosecond filamentation[J]. Optics Express, 2013, 21(4): 4740-4751. Doi:10.1364/OE.21.004740 |
| [35] |
Chang J W, Li D W, Xu L T, et al. Elongation of filamentation and enhancement of supercontinuum generation by a preformed air density hole[J]. Optics Express, 2022, 30(10): 16987-16995. Doi:10.1364/OE.458128 |
| [36] |
Vinçotte A, Bergé L. Femtosecond optical vortices in air[J]. Physical Review Letters, 2005, 95(19): 193901. Doi:10.1103/PhysRevLett.95.193901 |
| [37] |
Xi T T, Zhao Z J, Hao Z Q. Filamentation of femtosecond laser pulses with spatial chirp in air[J]. Journal of the Optical Society of America B, 2014, 31(2): 321-324. Doi:10.1364/JOSAB.31.000321 |
| [38] |
Wahlstrand J K, Jhajj N, Milchberg H M. Controlling femtosecond filament propagation using externally driven gas motion[J]. Optics Letters, 2019, 44(2): 199-202. Doi:10.1364/OL.44.000199 |
 2023, Vol. 40
2023, Vol. 40 


