2. 上海科技大学, 上海 201210
2. ShanghaiTech University, Shanghai 201210, China
低轨卫星(low earth orbit,LEO)以星地链路时延小、对天线尺寸和功率要求更低,在全球通信系统中一直具有重要的地位[1]。以低轨卫星与地面第五代通信(5th generation mobile communication technology,5G)融合的场景为例,低轨卫星通信要适应完善的产业链、巨大的用户群体、灵活高效的应用服务模式。在硬件资源有限的低轨卫星通信环境下,采用性能高和收敛高的信道编码是提高通信效率的有效途径。
Turbo码和低密度奇偶校验(low density parity check,LDPC)码是低轨卫星通信中常用的信道编码方式[2-3],它们均有接近香农极限的译码性能[4-5]。极化码是一种基于信道极化理论的信道编码[6-7],它被证明在二进制离散无记忆对称信道上能达到香农极限[8],且在中短码长下优于turbo码和LDPC码[9]。文献[10]中对极化码在卫星通信中的应用进行研究, 文献[11]中分析极化码在ka波段卫星通信中的性能。以上研究表明极化码在卫星通信系统中具有良好的应用前景,但同时也存在复杂度高、占用硬件资源多的制约问题。本文从译码算法复杂度角度出发,对极化码译码算法进行优化,以适应硬件资源有限的卫星通信环境。
连续取消(successive cancellation,SC)译码器是极化码最经典的译码方法,但它在码长较短或中等时不够可靠。对任何信息位的不正确译码会在后续的译码中传播,导致严重的译码错误。文献[12]提出连续取消列表(successive cancellation list,SCL)译码算法,SCL译码器在每个译码阶段同时考虑L条译码路径,以降低译码错误的风险。文献[13-14] 提出循环冗余校验辅助连续取消列表(cyclic redundancy check aided successive cancellation list, CRC aided SCL,CA-SCL)译码器,使其译码性能进一步提升。尽管CA-SCL译码器具有优秀的译码性能,但它的运算复杂度和硬件资源消耗较大,并且随着列表大小的增长而增加。
关键集在文献[15]中被提出,用于优化极化码比特反转译码器。关键集是一组部分信息位的节点组成的集合,该集合被证明有极大概率(>99 %)包含SC译码中第1个出现的错误位。
本文将CA-SCL译码器与关键集以及自适应算法相结合,提出一种优化的CA-SCL译码器(optimized CA-SCL,OCASCL),以减少运算复杂度和资源消耗。OCASCL译码器相比经典CA-SCL译码器,在性能更优的情况下可减少65 % ~70 % 运算复杂度。OCASCL对复杂度的优化只取决于码块中信息位的排列,而不取决于信道环境。
1 极化码译码和关键集 1.1 极化码令
| $ {\boldsymbol{x}}_1^N={\boldsymbol{u}}_1^N {\boldsymbol{G}}_N={\boldsymbol{u}}_1^N {\boldsymbol{B}}_N {\boldsymbol{F}}^{\otimes n}. $ | (1) |
其中:x1N=(x1, x2, …, xN) 是一个已编码的比特序列,u1N=(u1, u2, …, uN) 是编码比特序列。极化码可以进一步表示为
| $ {\boldsymbol{x}}_1^N={\boldsymbol{u}}_A {\boldsymbol{G}}_N({\boldsymbol{A}}) \oplus {\boldsymbol{u}}_{{\boldsymbol{A}}^c} {\boldsymbol{G}}_N\left({\boldsymbol{A}}^c\right). $ | (2) |
其中:A是包含信息位的子集,Ac是包含冻结位的子集。冻结位为不包含信息量的节点。A和Ac由比特索引u1N区分。GN(A) 表示A中带索引的行形成的GN的子矩阵。GN(Ac) 表示Ac中带索引的行形成的GN的子矩阵。uA表示信息比特, uAc表示冻结比特。SC译码器可以非常有效地对极化码进行译码。它的译码复杂度为O(NlogN) 并且当N趋于无穷时,可以达到信道容量。
CA-SCL是极化码常用的译码算法之一。循环冗余校验(cyclic redundancy check,CRC)是一种循环冗余校验技术,通过CRC校验,可以判断出本次译码的结果是否正确。CA-SCL译码器将对SCL译码器L条路径产生的结果依次进行CRC校验,从通过校验的结果中选取最终的译码结果。相比SCL译码器,CA-SCL译码器具有更优的译码性能。
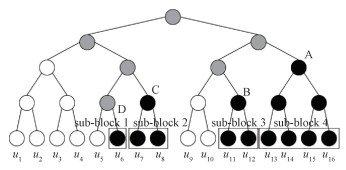
1.2 关键集和优化集以块长度为N=16和信息序列为u116 =(u1, u2, …, u16)的极化码为例,选择u68和u1116作为信息位。图 1所示为一棵有N=16个叶子节点的二叉树。冻结位的节点用白圈表示,信息位的节点用黑圈表示。对于树中的每个非叶节点,如果它的2个子节点是相同的颜色,那么它也会被标记为该颜色。否则,它将被标记为一个灰色的圆圈。这个过程会从树的底部到顶部进行。在图 1中,存在4棵黑树,分别用对应的根节点A、B、C、D表示。黑树只由黑色节点组成,并将其所有的叶节点定义为一个子块。例如,黑树A中的子块包含信息位u13 16,黑树D中的子块只包含1个信息位u6。
|
Download:
|
| 图 1 关键集生成二叉树 Fig. 1 Binary tree generate critical set | |
假设一棵一般的黑树,它包含M=2m个信息位,使用k1M和c1M分别表示其信息序列和码字。文献[16]中给出以下命题:
命题1 对于一个二进制擦除信道(BEC),当且仅当k1被正确译码时,整个子块才能被正确译码。
命题2 将整个子块的误码概率表示为Ps_bler,可得到
为了说明关键集对CA-SCL译码器复杂度的优化原理,本文针对极化码定义一种优化集:只选择少量信息位的节点(这些节点可以是随机选择、均匀选择或以某种特殊规律选择),并将这些节点形成一个集合。当优化集中的节点数量与关键集中的节点数量相同时,关键集就是优化集中的一种特殊情况。
2 OCASCL译码器 2.1 CA-SCL译码器与优化集结合定义2个在信息位的节点的操作:
操作A 类似于SC译码的操作,将每个当前译码路径分成2条路径,选择一个更好的保留。
操作B 包含2种类型的操作。操作B1发生在路径数达到L之前,将每个译码路径分成2条路径,并保存2条路径;操作B2,将每个译码路径分成2条路径,并对它们进行排序以保存最佳的L条路径。
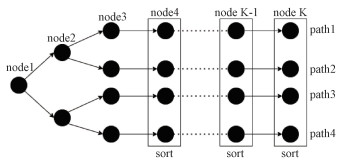
CA-SCL译码器操作过程如图 2所示,在路径数达到L之前,在每个信息位节点上,每条路径分裂成2条,并将这些路径均保留下来。当路径数达到L时,每条路径分裂成2条,对生成的2L条路径的可能性进行排序(极大地增加了复杂度),丢弃译码结果差的L条路径,保留译码结果好的L条路径。
|
Download:
|
| 图 2 CA-SCL译码器译码过程 Fig. 2 CA-SCL decoder decoding process | |
以4路径译码器为例,其中黑节点表示操作B,白节点表示操作A(本例中没有白节点)。CA-SCL译码器在每个信息位的节点中使用操作B。由于在每个信息位节点,路径数量都会增加1倍,所以只需要log2 L个信息位节点路径数量就能达到L。本例中第3个节点之后就达到最大路径数量,之后每个节点都要执行复杂的排序操作,因此复杂度大大提高。
根据CA-SCL的译码过程,有2种方法可以简化复杂度:1)将路径数达到L的节点延后,从而减少译码过程中的排序;2)在路径数达到L后,不对每个信息位的节点进行排序操作。
对此本文提出一种新的方法:在译码的过程中,对优化集中的节点执行B操作,其他节点执行操作A,该操作可以推迟路径达到L的节点,显著减少排序和操作次数,减少复杂度。
结合优化集的CA-SCL译码器步骤如下:
1) 当前译码节点为首个节点;
2) 对当前译码节点属性进行判断,如果为优化集中的节点跳转到步骤3);如果为信息位但不在优化集中跳转到步骤4);如果为冻结位跳转到步骤5);
3) 对该节点进行操作B,跳转到步骤6);
4) 对该节点进行操作A,跳转到步骤6);
5) 不对该节点分裂或排序操作,跳转到步骤6);
6) 若当前节点为最后1个节点,进行CRC校验并且选择出最后结果;若不是最后1个节点,当前节点变为下一个节点,跳转到步骤1)。
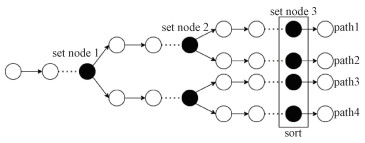
优化后的译码器模型如图 3所示。
|
Download:
|
| 图 3 CA-SCL译码器与优化集结合的模型 Fig. 3 A model combining CA-SCL decoder with optimization set | |
路径数达到L的节点延迟。在路径到达L后,也只对部分节点执行排序操作。对于更一般的情况,这2个译码器的操作数量如下:
对于CA-SCL译码,节点的操作数量为
| $ N_t=\sum\limits_{i=0}^{\log _2 L-1} 2^i+(K-\log L) L . $ | (3) |
其中:K是信息节点的数量,L是路径的数量。
所有排序需要的操作数量为
| $ N_s=\left(K-\log _2 L\right) L \log _2 L . $ | (4) |
其中Llog2L是长为L的序列排序需要的操作数量。CA-SCL译码器完整译码需要的操作总数为
| $ \begin{gathered} N_{\mathrm{SCL}}=N_t+N_s=\sum\limits_{i=0}^{\log _2 L-1} 2^i+(K-\log L) L+ \\ \left(K-\log _2 L\right) L \log _2 L . \end{gathered} $ | (5) |
对于优化CA-SCL译码器,节点操作数为
| $ N_t=\frac{K}{S} \sum\limits_{i=0}^{\log _2 L} 2^i+\left(K-\frac{K}{S} \log L\right) L . $ | (6) |
其中S是优化集中的节点数。
所有排序需要的操作数量为
| $ N_s=\left(S-\log _2 L\right) L \log _2 L . $ | (7) |
优化CA-SCL译码器完整译码需要的操作总数为
| $ \begin{gathered} N_{\mathrm{SCLSET}}=N_t+N_s=\frac{K}{S} \sum\limits_{i=0}^{\log _2 L} 2^i+ \\ \left(K-\frac{K}{S} \log L\right) L+\left(S-\log _2 L\right) L \log _2 L . \end{gathered} $ | (8) |
假设K=512和S=128,表 1显示结合了优化集的CA-SCL译码器可以显著减少操作的次数。当L=32时,操作量节省65 % 以上。
|
|
表 1 CA-SCL与结合优化集的CA-SCL的操作数量比较 Table 1 Comparison of the number of operations between CA-SCL and CA-SCL combined with optimization sets |
仿真实验采用高斯信道(AWGN),输入为码长为1 024的信号。实验中信道环境由每比特信号能量和噪声功率谱密度的比值Eb/N0(Eb为比特的平均能量,N0为单边噪声功率谱密度)表示,其中Eb/N0的单位为dB。
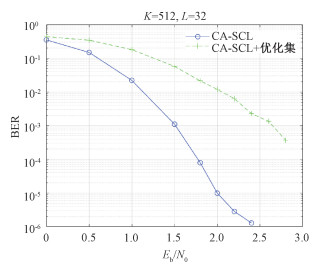
图 4显示CA-SCL译码器与结合优化集(随机选择或均匀选择)的CA-SCL译码器译码性能仿真结果的比较。结合优化集(随机选择或均匀选择)的CA-SCL译码器的性能远远低于经典的CA-SCL译码器。
|
Download:
|
| 图 4 CA-SCL与CA-SCL+优化集的译码性能的比较 Fig. 4 Comparison of decoding performance of CA-SCL and CA-SCL combines optimization set | |
由仿真结果得出,如果优化集中的节点是随机选择或均匀分布的,虽然它可以降低译码的复杂度,但其译码性能会显著降低。为保证算法的译码性能,本文提出使用关键集作为优化集对译码器优化。
2.2 CA-SCL译码器与关键集结合本文提出用关键集作为优化集对译码器进行优化。由于SC译码器译码时的第1个错误位出现在关键集的概率极高(超过99.9 %),因此在关键集的节点上使用操作B可以保存所有可能出错的结果。其他节点在译码时出错可能性极低,仅使用操作A并不会对译码性能产生影响。
对结合优化集的CA-SCL译码器来说,当优化集中的节点数量相同时(无论是均匀选择、随机选择或是关键集),其运算复杂度是相同的。因此使用关键集作为优化集,可以在不增加复杂度的情况下提高译码性能。
结合关键集的CA-SCL译码器步骤如下:
1) 当前译码节点为首个节点;
2) 对当前译码节点属性进行判断,如果为关键集中的节点跳转到步骤3);如果为信息位但不在关键集中跳转到步骤4);如果为冻结位跳转到步骤5);
3) 对该节点进行操作B,跳转到步骤6);
4) 对该节点进行操作A,跳转到步骤6);
5) 不对该节点分裂或排序操作,跳转到步骤6);
6) 若当前节点为最后1个节点,进行CRC校验并且选择出最后结果;若不是最后1个节点,当前节点变为下一个节点,跳转到步骤1)。
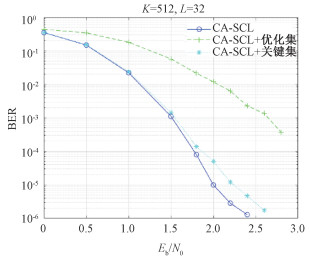
结合关键集的CA-SCL译码器译码性能在图 5显示。与结合优化集(随机或均匀选择节点)相比,使用关键集的译码性能更好。与CA-SCL译码器相比,当误码率为10-5时,译码性能降低0.2 dB。与此同时,它减少了65 % 的复杂度。为保证译码器的译码性能,本文提出将与关键集结合的CA-SCL译码器与自适应算法结合。
|
Download:
|
| 图 5 CA-SCL、CA-SCL+优化集以及CA-SCL+ 关键集的译码性能的比较 Fig. 5 Comparison of decoding performance of CA-SCL, CA-SCL combines optimization set and CA-SCL combines critical set | |
在译码中采用自适应方法的思路是:首先使用低复杂度但性能较差的译码器进行译码,如SC译码器或少路径的SCL译码器,后通过CRC技术确定译码结果是否正确。如果译码结果没有通过CRC测试,则用高性能但复杂度也高的译码器进行译码。
OCASCL即是将结合关键集的CA-SCL译码器与自适应算法结合,其步骤如下:
1) 仅结合关键集的CA-SCL译码器进行译码;
2) 对每个留存的路径进行CRC检查;
3) 如果有1条或多条路径通过CRC检查,则通过CRC检查且概率最高的路径为结果,并退出译码;否则跳转步骤4);
4) 使用经典CA-SCL译码,CA-SCL结果为最终结果。
虽然结合关键集的CA-SCL译码器译码性能低于经典的CA-SCL译码器,但其译码错误的概率也非常低。例如当Eb/N0为1.5 dB时,结合关键集的CA-SCL译码器误码率为10-3,即1 000个比特中只有1个比特译码错误。OCASCL译码器仅会在结合关键集的CA-SCL译码器译码出错时,自适应地使用经典CA-SCL译码器进行译码。因此可以在增加很少复杂度情况下提高译码性能。OCASCL译码器平均需要的操作数为
| $ N_{{\text {AdaplSCLset }}}=N_{{\text {SCLSET }}}+({\text { Err_bler }} / {\text { Frame }}) N_{{\text {SCL }}} . $ | (9) |
其中:Err_bler是错误译码的块的数量,Frame是块的总数。
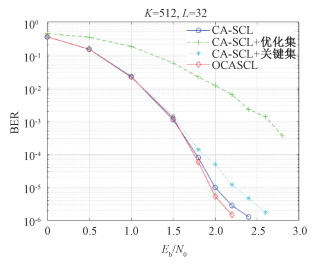
如表 2所示,当Eb/N0>2,码长为1 024,译码路径为32,误码率为10-5时,OCASCL译码器相比仅结合关键集的CA-SCL的复杂度几乎相同,相比经典CA-SCL译码器复杂度降低65 %。此外,译码性能结果如图 6所示,OCASCL译码器相比结合关键集的CA-SCL译码算法性能有所提升。当码长为1 024,译码路径为32,误码率为10-5时,OCASCL译码器的性能优于经典的CA-SCL译码器0.012 dB。
|
|
表 2 OCASCL译码器的操作数量 Table 2 The number of operations of the OCASCL decoder |
|
Download:
|
| 图 6 CA-SCL、CA-SCL+优化集、CA-SCL+关键集以及OCASCL译码性能的比较 Fig. 6 Comparison of decoding performance of CA-SCL, CA-SCL combines optimization set, CA-SCL combines critical set, and OCASCL | |
本文提出一种低复杂度的CA-SCL译码器的优化模型(OCASCL译码器),它融合了关键集以及自适应算法。与关键集结合的译码器只对关键集中的节点进行分裂和排序操作。与关键集相结合的CA-SCL译码器再与自适应算法相结合,可以保持在显著降低复杂度的情况下,译码性能更优。当码长为1 024,译码路径为32,误码率为10-5时,OCASCL译码器的性能优于经典的CA-SCL译码器0.012 dB,操作次数减少65 % ~70 %。OCASCL译码器可以有效适应硬件资源有限的低轨卫星通信环境。
| [1] |
Wu W W, Miller E F, Pritchard W L, et al. Mobile satellite communications[J]. Proceedings of the IEEE, 1994, 82(9): 1431-1448. Doi:10.1109/5.317086 |
| [2] |
Kalmykov I A, Mukhametshin V Sh, Tyncherov K T, et al. Developing method for constructing modular turbo code for anti-jam satellite authentication system[J]. Journal of Physics: Conference Series, 2022, 2176(1): 012023. Doi:10.1088/1742-6596/2176/1/012023 |
| [3] |
Zhang C, Mu X J, Yuan J H, et al. Construction of multi-rate quasi-cyclic LDPC codes for satellite communications[J]. IEEE Transactions on Communications, 2021, 69(11): 7154-7166. Doi:10.1109/TCOMM.2021.3107578 |
| [4] |
Berrou C, Glavieux A, Thitimajshima P. Near Shannon limit error-correcting coding and decoding: turbo-codes. 1[C]//Proceedings of ICC'93-IEEE International Conference on Communications. May 23-26, 1993, Geneva, Switzerland. IEEE, 2002: 1064-1070. DOI: 10.1109/ICC.1993.397441.
|
| [5] |
MacKay D J C, Neal R M. Near Shannon limit performance of low density parity check codes[J]. Electronics Letters, 1996, 32(18): 1645. Doi:10.1049/el:19961141 |
| [6] |
Arikan E. Channel polarization: a method for constructing capacity-achieving codes for symmetric binary-input memoryless channels[J]. IEEE Transactions on Information Theory, 2009, 55(7): 3051-3073. Doi:10.1109/TIT.2009.2021379 |
| [7] |
Wang H P, Duursma I M. Polar codes'simplicity, random codes'durability[J]. IEEE Transactions on Information Theory, 2020, 67(3): 1478-1508. Doi:10.1109/TIT.2020.3041570 |
| [8] |
Şaşoǧlu E, Telatar E, Arikan E. Polarization for arbitrary discrete memoryless channels[C]//2009 IEEE Information Theory Workshop. October 11-16, 2009, Taormina, Italy. IEEE, 2009: 144-148. DOI: 10.1109/ITW.2009.5351487.
|
| [9] |
Meng Y, Fang Y, Zhang C, et al. LLR processing of polar codes in concatenation systems[J]. China Communications, 2019, 16(9): 201-208. Doi:10.23919/JCC.2019.09.015 |
| [10] |
赵昕柔. 极化码在卫星通信中的应用研究[D]. 西安: 西安电子科技大学, 2020.
|
| [11] |
Chen Y Y, Wang Y Z, Dong Y. Performance analysis of polar codes against rain attenuation in ka-band satellite communication[C]//2021 International Conference on Communications, Information System and Computer Engineering (CISCE). May 14-16, 2021, Beijing, China. IEEE, 2021: 146-150. DOI: 10.1109/CISCE52179.2021.9445972.
|
| [12] |
Chen K, Niu K, Lin J R. List successive cancellation decoding of polar codes[J]. Electronics Letters, 2012, 48(9): 500. Doi:10.1049/el.2011.3334 |
| [13] |
Niu K, Chen K. CRC-aided decoding of polar codes[J]. IEEE Communications Letters, 2012, 16(10): 1668-1671. Doi:10.1109/LCOMM.2012.090312.121501 |
| [14] |
Tal I, Vardy A. List decoding of polar codes[J]. IEEE Transactions on Information Theory, 2015, 61(5): 2213-2226. Doi:10.1109/TIT.2015.2410251 |
| [15] |
Zhang Z Y, Qin K J, Zhang L, et al. Progressive bit-flipping decoding of polar codes: a critical-set based tree search approach[J]. IEEE Access, 2018, 6: 57738-57750. Doi:10.1109/ACCESS.2018.2873821 |
| [16] |
Zhang Z Y, Qin K J, Zhang L, et al. Progressive bit-flipping decoding of polar codes over layered critical sets[C]//GLOBECOM 2017-2017 IEEE Global Communications Conference. December 4-8, 2017, Singapore. IEEE, 2018: 1-6. DOI: 10.1109/GLOCOM.2017.8254149.
|
 2024, Vol. 41
2024, Vol. 41 


