随着智能化技术的发展,空间机器人在轨服务技术目前已是世界上航天大国研究的热点之一[1-2],例如日本在1997年发射的EST-Ⅶ[3],美国DARPA的轨道快车计划于2007年在轨试验成功[4]。我国运载火箭技术研究所的“遨龙一号”空间机器人也于2016年6月完成空间飞行试验[5]。但是单个空间机器人由于其自身尺寸、能源以及燃料等方面的限制,只能针对单个小型的目标航天器进行在轨操作,无法完成较大规模的在轨服务任务。如果要针对大型航天器进行在轨服务,例如空间站的在轨维护[6]、高轨大型通信卫星的维护[7],或者是大型航天器和大尺寸设备的在轨制造等任务[6, 8],则要将多个微纳卫星空间机器人组合成为一个空间机器人集群,同时对同一个目标航天器进行多段在轨操作,方可有效提升任务效率。虽然集群可以提升整个在轨服务任务的效率,但是限于目前的技术水平,微纳卫星空间机器人的电源功率相当紧张。空间机器人能耗主要分为传感器功耗、在轨操作设备功耗和数据通信功耗。其中传感器和在轨操作设备的功耗是无法避免的,因此对于空间机器人来说可以优化的功耗就只有通信方向的功耗。而图像等大数据量传输所需的无线通信功耗较大,当采集目标航天器数据并与数据中枢卫星进行通信时,需要严格控制和规划集群通信方式以尽可能地减少用于通信的功耗、延长空间机器人的活动时间,进而增强集群整体性能。
当前针对空间机器人的集群通信研究较少,无人机集群的集群通信与集群中心节点的选择问题是研究热点。例如将邻居节点的数量作为衡量指标的,有度中心性算法[9]和半局部中心性算法[10]。文献[11]引用信息熵的概念同时考虑节点的度中心性与邻居节点的度中心性。文献[12]提出K-壳分解(K-shell decomposition, K-shell)方法,将大规模的网络节点通过不同的度值层层分解并赋予不同权重值,越是中心层的节点权重越高。文献[13-14]分别对K-shell算法进行优化,文献[13]考虑了局部指标超度与全局位置指标K-shell,而文献[14]则将K-Shell算法与邻居节点之间的相互作用和时间维度上的传播状态相结合,提出KIC算法。文献[15]则考虑在删除某一重要节点后如何规划信息传播最短路径并进行选择。文献[16]基于删除节点对的思想,通过信息存量和信息流量来选择无向网络中的关键节点对。文献[17]利用度中心性、接近中心性和介数中心性3个指标计算节点的接近度并选取接近度最大的为集群的中心节点。目前集群中心节点的算法主要采用图论相关知识,将整个集群视为一个有向或无向的图进行相应的中心节点选择。虽然利用图论相关知识可以有效地分析集群中的一些拓扑特征,但是对于一个实际的集群通信系统来说,其通信功耗不是只由网络结构决定,还和节点中的数据量大小有关。尤其是空间机器人集群中心节点还需要与长距离的数据中枢卫星通信,那么最后由中心节点向数据中枢卫星通信的功耗会占据整个集群通信功耗的主要部分,因此对于集群通信网络中数据和数据压缩的研究具有重要意义。
本文针对空间机器人集群在进行非合作目标航天器相关特征数据采集与分析时的集群通信功耗最优问题,提出一种基于数据和数据压缩率预测的空间机器人集群中心节点选择算法(data and data compression ratio prediction,DCP)。通过分析空间机器人对于目标航天器数据采集与数据的可压缩性特点,采用高斯分布模型对目标航天器采样数据进行预测,并通过集群的轨迹变化预测集群间通信时不同空间机器人数据对中心节点的数据可压缩性,从而选择合适的集群中心节点以最小化整个系统的通信功耗。与固定中心算法(fixed point, Fix)、度中心性算法(degree centrality, DC)、介数中心性算法(betweenness centrality, BC),以及接近中心性算法(closeness centrality, CC)相比,提出的DCP算法可以有效地逼近实际的最优集群通信功耗。该算法可以被应用于后期的空间机器人集群项目。
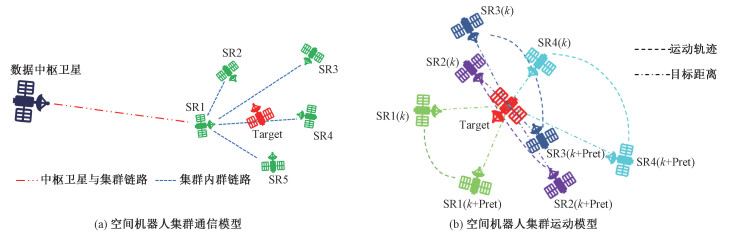
1 系统模型与问题描述 1.1 空间机器人集群模型如图 1(a)所示,空间机器人集群主要由一个大型的数据中枢卫星和多个微纳卫星空间机器人组成。当执行在轨任务时,较大型的数据中枢卫星会与目标航天器保持一定的安全距离,避免通信遮挡以便于对整体集群进行第三视角导航。多个微纳卫星空间机器人分工合作,专注于测量、导航和服务,往往不具备仅在阳照区对日才能产生效能的太阳电池翼,只携带电池提供单次任务较短时的供电。关于空间机器人集群的运动,如图 1(b)所示,由多个微纳卫星空间机器人自主地靠近目标航天器,并且短时间内按照一定轨迹绕飞于目标航天器,以收集目标航天器的相关三维和细节特征数据并将其传输至数据中枢卫星。空间机器人集群的运动轨迹由集群在靠近目标时自主规划,并且会随着目标数据的收集和后续任务目标点的确定进行轨迹的重新规划。同时由于控制算法和传感器的限制,实际的运动轨迹与理想中规划的运动轨迹会存在一定偏差。空间机器人集群将收集的目标航天器数据传输到大型数据中枢卫星的步骤如下:首先在集群内部将数据集中于一个空间机器人,然后由被选择作为中心节点的空间机器人将集群在当前时刻采集的目标数据传输到数据中枢卫星进行下一步处理。
|
Download:
|
| 图 1 空间机器人集群模型 Fig. 1 Space robot swarm model | |
如图 1所示,假设空间机器人集群中包含有Nsr个微纳卫星空间机器人,大型的数据中枢卫星距离目标航天器距离为D0,目标航天器位置矢量为 pt。对于空间机器人i来说,在k时刻相关变量如表 1所示。
|
|
表 1 系统模型符号 Table 1 System model symbols |
则空间机器人j在k时刻向空间机器人i通信的功耗Pi, j(k)为
| $ \begin{gathered} P_{i, j}(k)=\left(\left[\frac{d_i(k)}{d_{\max }}\right]+1\right)\left(P_{i, j}\left(k, D_{i, j}(k)\right)+\right. \\ \left.L_{i, j}\left(k, D_{i, j}(k)\right)\right), \end{gathered} $ | (1) |
空间机器人i在k时刻作为集群主节点向数据中枢卫星通信时,整个集群通信功耗Pi(k)为
| $ \begin{aligned} & P_i(k)=\sum\limits_{j!=i}^{N_{\mathrm{sr}}} P_{i, j}(k)+\left(P_{i, 0}(k)+\right. \\ & \left.L_{i, 0}(k)\right)\left(\left[\frac{\sum_{j=1}^{N_{s r}} C_{i, j}(k) d_j(k)}{d_{\max }}\right]+1\right). \end{aligned} $ | (2) |
综上可得,空间机器人集群的最优通信功率问题,可以视为在k时刻选取一个最优的集群主节点使得整个集群的通信功率消耗最小:
| $ \mathop {\min }\limits_{{\rm{index}}} {P_{{\rm{index}}}}\left( k \right). $ | (3) |
| $ {{\text { s. t. }}} 0<C_{i, j}(k) \leqslant 1. $ | (4) |
对于空间机器人集群通信问题来说,在通信机功率确定的情况下,决定其整个集群通信总功率的变量主要有数据中枢卫星与空间机器人的距离、集群内部不同空间机器人之间的通信距离以及空间机器人的通信数据量。由于本研究中假设数据中枢卫星与目标之间保持恒定的距离,而空间机器人集群的运动轨迹则是规划完成的,所以可以通过空间机器人集群的数据与数据压缩率的预测来预测集群总通信功率,从而选择最优的集群中心节点以获得最优的集群通信功耗。
2.2 算法描述基于以上分析,本文提出一种基于空间机器人采集数据与数据压缩比预测的集群网络最优主节点选择算法。该算法主要是通过当前时刻空间机器人的理想轨迹变化与实际的轨迹变化推导出一个数据的高斯分布以预测k+Pret时刻的数据大小;然后通过集群内部的不同空间机器人相对位姿的变化推导未来时刻的数据压缩比;最后通过预测的数据与压缩比计算空间机器人集群的总通信功耗,从而选择合适的集群中心节点以获得最优的集群通信功耗。
2.2.1 数据预测由于数据收集采用的是定时收集的策略,因此目标航天器在传感器中的成像大小和细节特征会呈现近大远小的特点。采用统一的数据编码压缩算法,则目标数据的大小与空间机器人和目标航天器之间的距离成负相关。对于空间机器人来说,它在k时刻采集的目标航天器数据主要和它与目标航天器的距离有关,而不同时刻下该数据大小的变化只与2个时刻间空间机器人i的轨迹变化有关,因此在k时刻下空间机器人i的轨迹变化为
| $ \Delta p_i(k+{\text { Pret }})=\mid {\boldsymbol{p}}_{i, {\text { ideal }}}(k+{\text { Pret }})-\left.{\boldsymbol{p}}_{i, {\text { real }}}(k)\right|_2, $ | (5) |
| $ \Delta p_{i, r}(k)=\left|{\boldsymbol{p}}_{i, {\text { ideal }}}(k)-{\boldsymbol{p}}_{i, {\text { real }}}(k)\right|_2, $ | (6) |
| $ \Delta p_{i, e}(k)=\left|{\boldsymbol{p}}_{i, {\text { real }}}(k)-{\boldsymbol{p}}_{i, {\text { real }}}(k-1)\right|_2, $ | (7) |
| $ \Delta p_{i, t}(k+{\text { Pret }})=D_{i, T}(k+{\text { Pret }})-D_{i, T}(k). $ | (8) |
同时空间机器人对于目标航天器的采集数据变化为
| $ \Delta d_{i, e}(k)=\left|d_i(k)-d_i(k-1)\right|, $ | (9) |
| $ \Delta d_{i, p}(k)=\left|d_i(k)-d_{i, {\mathrm{pre}}}(k)\right|, $ | (10) |
| $ \mu_{d_i, N}(k)=\frac{1}{N} \sum\limits_{j=k-N}^N d_i(j), $ | (11) |
联合以上式子可得出k+Pret时刻的空间机器人i的采集数据所属高斯分布的均值μi(k+Pret)与方差δi2(k+Pret) 为
| $ \begin{gathered} \mu_i(k+{\text { Pret }})=F\left(\Delta p_i(k+{\text { Pret }}), \Delta p_{i, t}(k+{\text { Pret }}), \right. \\ \left.\Delta d_{i, e}(k), \Delta p_{i, e}(k)\right)+\mu_{d_i, {\text { Pret }}}(k), \end{gathered} $ | (12) |
| $ \begin{gathered} \delta_i^2(k+{\text { Pret }})=\alpha G\left(\Delta d_{i, p}(k), \Delta p_{i, r}(k)+1\right)+ \\ \beta \delta_i^2(k), \end{gathered} $ | (13) |
其中F(Δpi(k+Pret), Δpi, t(k+Pret), Δdi, e(k), Δpi, e(k))与G(Δdi, p(k), Δpi, r(k)+1)可以表示为
| $ F(a, b, c, d)={\rm{sgn}}(b)\left(\frac{a c}{d}+\log _{10}(b)\right), $ | (14) |
| $ G(a, b)=\frac{a}{b+1} . $ | (15) |
因此对于k+Pret时刻可以得到预测的采集数据di, p(k+Pret)大小为
| $ d_{i, p}(k+{\text { Pret }})=\mu_i(k+{\text { Pret }})+\sqrt{\delta_i^2(k+{\text { Pret }})} X. $ | (16) |
其中X为服从标准高斯分布的随机变量。数据预测算法的步骤如算法1所示。
算法1 数据预测
Input: 空间机器人集群轨迹变化、数据变化
Output: 空间机器人集群采样数据预测
1: for each i∈[1, Nsr] do
2: μi(k+Pret)可由联立式(5)(7)(8)(9)(11)(12)(14)获得
3: δi2(k+Pret) 可由联立式(6)(10)(13)(15)获得
4: di, p(k+Pret)可由联立式(12)(13)(16)获得
5: end for
6: return di, p(k+Pret)
根据上述分析,当2个空间机器人之间的轨迹满足一定要求时,双方对于目标航天器采集的数据会存在一定压缩特性。空间机器人的数据压缩率主要由双方之间的距离、相关角度以及接收后的数据质量所决定。当数据由一个节点向另一个节点传输时,由于传输信道的噪声和传输距离的长度会对传输数据造成一定的质量下降,因此可通过数据质量表示当前传输后的数据相比于原始数据的损失。k时刻空间机器人相关特性变量θ与数据质量Qi, j(k+Pret)为
| $ {\boldsymbol{v}}_1={\boldsymbol{p}}_{i, {\text { ideal }}}(k+{\text { Pret }})-{\boldsymbol{p}}_t(k), $ | (17) |
| $ {\boldsymbol{v}}_2={\boldsymbol{p}}_{j, {\text { ideal }}}(k+{\text { Pret }})-{\boldsymbol{p}}_t(k), $ | (18) |
| $ \theta=2 \arccos \left(\frac{v_1\left(v_1+v_2\right)}{\left|v_1\right|_2\left|v_1+v_2\right|_2}\right), $ | (19) |
| $ {\boldsymbol{p}}_{i, p}(k+{\text { Pret }})=\sqrt{\frac{\sum_{m=k-N}^{k-1} \Delta p_{i, r}(m)}{2 N}+\frac{\Delta p_{i, r}(k)}{2}} X+\\{\boldsymbol{p}}_{i, {\text { ideal }}}(k+{\text { Pret }}), $ | (20) |
| $ \begin{aligned} & {\boldsymbol{p}}_{j, p}(k+{\text { Pret }})= \sqrt{\frac{\sum_{m=k-N}^{k-1} \Delta p_{j, r}(m)}{2 N}+\frac{\Delta p_{j, r}(k)}{2}} X+ \\ & {\boldsymbol{p}}_{j, {\text { ideal }}}(k+{\text { Pret }}), \end{aligned} $ | (21) |
| $ \begin{gathered} Q_{i, j}(k+{\text { Pret }})= \\ \frac{2 R-\mid p_{i, p}(k+{\text { Pret }})-\left.{\boldsymbol{p}}_{j, p}(k+{\text { Pret }})\right|_2}{2 R}, \end{gathered} $ | (22) |
其中R为空间机器人运动半径。由以上可以得到空间机器人之间的数据压缩率Ci, j, p(k+Pret)为
| $ C_{i, j, p}(k+{\text { Pret }})= \begin{cases}1, & \theta>\theta_{\rm{t}} , \\ \log _2\left(\frac{\mid {\boldsymbol{p}}_{i, p}(k+{\text { Pret }})-\left.{\boldsymbol{p}}_{j, p}(k+{\text { Pret }})\right|_2}{2 R}+1\right)\left(1-Q_{i, j}(k+{\rm{Pret}})\right) \log _2\left(\frac{2 \theta}{{\boldsymbol{\pi}}}+1\right), & \theta \leqslant \theta_{\rm{t}}.\end{cases} $ | (23) |
其中θt为相关角的阈值。数据的压缩率预测算法的步骤如算法2所示。
算法2 数据压缩率预测
Input: 空间机器人集群轨迹变化
Output: 空间机器人集群的数据压缩率预测
1: for each i∈[1, Nsr] do
2:
for each j∈[1, Nsr] do
3:
v1式(17)
4:
v2式(18)
5:
θ可由联立式(17)(18) 获得
6:
if θ>θt then
7:
Ci, j, p(k+Pret)=1
8:
else
9:
pi, p(k+Pret)可由联立式(6)(20)获得
10:
pj, p(k+Pret) 可由联立式(6)(21)获得
11:
Qi, j(k+Pret) 可由联立式(20)(21)获得
12:
Ci, j, p(k+Pret) 可由联立式(19)(20)(21)(22)(23)获得
13:
end if
14:
end for
15: end for
16: return Cp(k+Pret)
根据上述得到的空间机器人在k时刻的预测数据和压缩比,可以对整个空间机器人集群的通信功率做出预测。当选择空间机器人i为集群的中心节点时,集群的通信功耗Pi, p(k+Pret)为
| $ \begin{gathered} P_{i, p}(k+{\text { Pret }})=\sum\limits_{j!=i}^{N_{\mathrm{sr}}} P_{i, j}(k+{\text { Pret }})+ \\ \left(P_{i, 0}(k+{\text { Pret }})+L_{i, 0}(k+{\text { Pret }})\right)\left(d_{i, s}(k+{\text { Pret }})\right), \end{gathered} $ | (24) |
| $ \begin{gathered} d_{i, s}(k+{\text { Pret }})= \\ {\left[\frac{\sum_{j=1}^{N_{\mathrm{sr}}} C_{i, j, p}(k+{\text { Pret }}) d_{j, p}(k+{\text { Pret }})}{d_{\max }}\right]+1}, \end{gathered} $ | (25) |
可以利用矩阵的形式同时计算不同集群中心节点的集群通信总功耗Pp(k+Pret)为
| $ \begin{gathered} {\boldsymbol{P}}_p(k+{\text { Pret }})={\boldsymbol{P}}_{i, p}(k+{\text { Pret }}) v+\left(P_{i, 0}(k+{\text { Pret }})+\right. \\ \left.L_{i, 0}(k+{\text { Pret }})\right) {\boldsymbol{C}}_p(k+{\text { Pret }}) {\boldsymbol{d}}_p(k+{\text { Pret }}). \end{gathered} $ | (26) |
| $ \begin{aligned} {\boldsymbol{v}}= {[1, 1, 1, \cdots 1]^{\mathrm{T}} {\boldsymbol{d}}_p(k+{\text { Pret }})=\left[d_{1, p}(k+{\text { Pret }}), \right.} \\ \left.d_{2, p}(k+{\text { Pret }}), \cdots, d_{N_{\mathrm{sr} }, p}(k+{\text { Pret }})\right]^{\mathrm{T}}, \\ {\boldsymbol{P}}_{i, p}(k+{\text { Pret }})= \\ {\left[\begin{array}{ccc} P_{1, 1}(k+{\text { Pret }}) & \cdots & P_{1, N_{\mathrm{sr}}}(k+{\text { Pret }}) \\ \vdots & & \vdots \\ P_{N_{\mathrm{sr}}, 1}(k+{\text { Pret }}) & \cdots & P_{N_{\mathrm{sr}}, N_{\mathrm{sr}}}(k+{\text { Pret }}) \end{array}\right]},\\ {\boldsymbol{C}}_p(k+{\text { Pret }})= \\ {\left[\begin{array}{ccc} C_{1, 1, p}(k+{\text { Pret }}) & \cdots & C_{1, N_{\mathrm{sr}}, p}(k+{\text { Pret }}) \\ \vdots & & \vdots \\ C_{N_{\mathrm{sr}}, 1, p}(k+{\text { Pret }}) & \cdots & C_{N_{\mathrm{sr}}, N_{\mathrm{sr}}, p}(k+{\text { Pret }}) \end{array}\right]}. \end{aligned} $ |
通过以上公式计算得到k+Pret时刻的不同中心节点下的集群的总通信功耗 Pp(k+Pret),然后选择其中功耗最小的中心节点编号作为k+Pret时刻的空间机器人集群的中心节点indexopt(k+Pret),即
| $ \operatorname{index}_{{\text {opt }}}(k+{\text { Pret }})=\underset{{\text { index }}}{\operatorname{argmin}}\left({\boldsymbol{P}}_p(k+{\text { Pret }})\right). $ | (27) |
集群最优中心节点选择算法的步骤如算法3所示。
算法3 集群最优中心点选取
Input: 空间机器人集群的轨迹变化,预测数据、预测数据压缩率
Output: 空间机器人集群最优中心节点编号
1: for i∈[1, Nsr] do
2:
di, p(k+Pret)可由算法1获得
3:
for j∈[1, Nsr] do
4:
Ci, j, p(k+Pret)可由算法2获得
5:
end for
6: end for
7: Pp(k+Pret)可由联合算法1,算法2,式(26)获得
8: indexopt(k+Pret)可由式(27)获得
9: return indexopt(k+Pret)
本文使用Matlab软件2020b版本对整个空间机器人集群通信系统进行仿真,实验参数如表 2所示。本次实验将分别采用4、6、8和10集群作为不同空间机器人集群数量的对比。对比算法选择为Fix、DC、BC,以及CC。空间机器人集群的运动轨迹,是以目标航天器为球心、半径为150 m的球形空间内的随机轨迹,并且实际运动轨迹与理想运动轨迹之间存在一定的偏差。
|
|
表 2 实验参数设计 Table 2 Experimental parameter design |
基于上述实验参数和实验设计,通过Matlab仿真软件对DCP算法和Fix、BC、CC及DC算法进行比较。
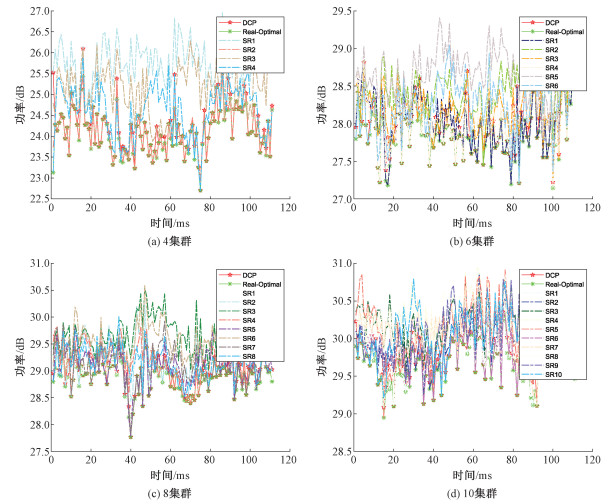
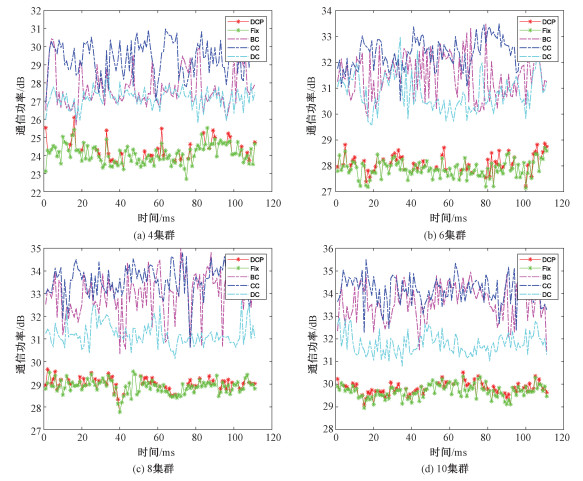
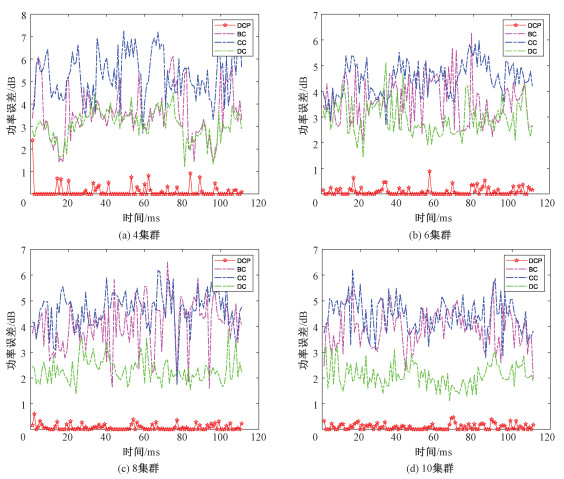
首先是对比DCP算法与Fix、BC、CC及DC算法的集群通信总功率。图 2为DCP算法与Fix算法的性能对比,可以看出相比于不同中心节点下的Fix算法,DCP算法有着更优的通信功耗,并且在不同的集群尺寸下它都可以选择合适的集群中心节点以保持最优的集群通信功耗。DCP算法与BC、CC及DC算法对比如图 3和图 4所示,相比其他的经典中心节点算法,DCP算法性能更接近实际的最优通信功耗。由图 4可以发现,BC、CC及DC算法的性能会随着集群的尺寸增长而有一定程度的提升,但是相比于DCP算法仍然有着较大的波动性。而DCP算法与实际的最优通信功耗之差在大部分情况下都接近于0,并随着集群尺寸的增长性能更加趋于稳定,说明DCP算法对于空间机器人集群的尺寸变化有着较好的鲁棒性。
|
Download:
|
| 图 2 不同集群大小下,不同中心节点、实际最优中心节点与预测最优中心节点通信功率 Fig. 2 Different central nodes, the actual optimal central node, and the predicted optimal central node communication power under different cluster sizes | |
|
Download:
|
| 图 3 不同集群大小下,实际最优中心节点与不同中心节点选择算法的通信功率 Fig. 3 Communication power between the actual optimal central node and different central node selection algorithms under different cluster sizes | |
|
Download:
|
| 图 4 不同集群大小下,实际最优中心节点与不同中心节点选择算法的通信功率之差 Fig. 4 Communication power difference between the actual optimal central node and different central node selection algorithms under different cluster sizes | |
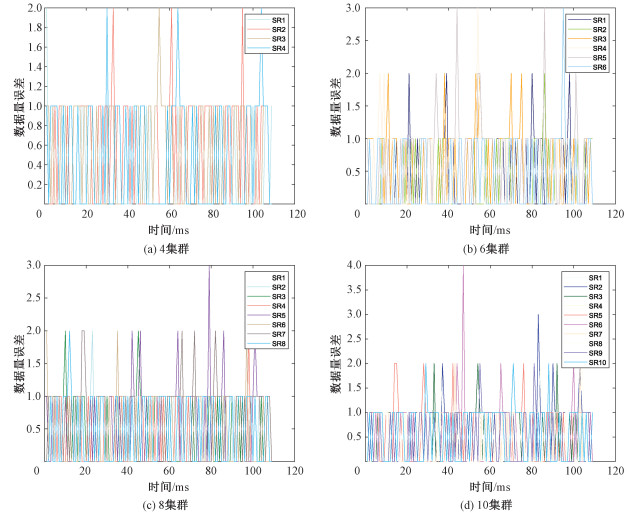
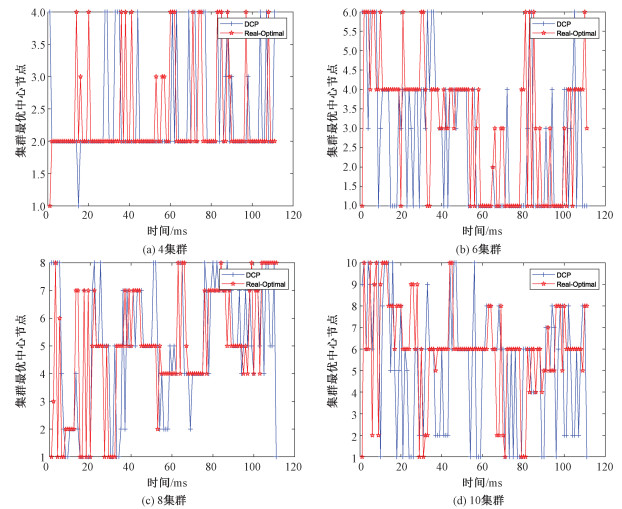
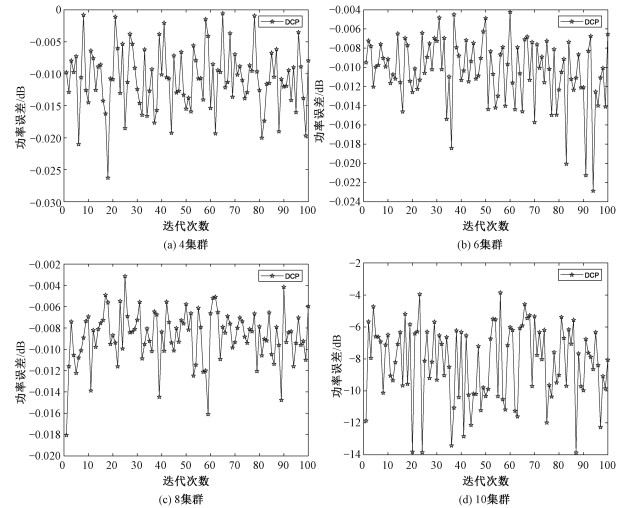
如图 5所示,当采用DCP算法对当前时刻的空间机器人数据量进行预测时,误差一般在一个数据包左右(即实际的数据误差小于一个dmax),最大也不超过4个数据包。对比不同的空间机器人集群大小,说明DCP算法对于数据的预测具有较强的鲁棒性,并不会随着集群大小的改变而发生较大波动。DCP算法计算的最优集群中心节点与实际最优的集群中心节点如图 6所示,可以看出在大部分情况下DCP算法预测出的最优集群中心节点与实际的最优集群中心节点相同。而在不同的集群大小情况下DCP算法的预测与实际最优的集群中心节点之间误差并无较大差距,证明DCP算法针对当前问题有着较好的鲁棒性。经过100次重复实验的DCP算法最优的集群总通信功耗与实际集群通信功耗误差如图 7所示,可以发现基于DCP算法预测出的集群通信总功率与实际的最优集群通信总功率之间的误差基本小于3 %。
|
Download:
|
| 图 5 不同集群大小下,空间机器人实际数据与预测数据误差 Fig. 5 Error between actual data and prediction data of space robots under different cluster sizes and different central nodes | |
|
Download:
|
| 图 6 不同集群大小下,实际最优与预测最优中心节点标号 Fig. 6 Actual optimal and predicted optimal center nodes under different cluster sizes | |
|
Download:
|
| 图 7 不同集群大小下,实际最优与预测最优中心节点总通信功率之差(100次重复实验) Fig. 7 Difference between the actual optimal and the predicted optimal central node total communication power (100 times the experiment was repeated) under different cluster sizes | |
综上所述,与Fix算法相比,DCP算法可以有效地实现空间机器人集群的数据和数据压缩率的预测,并且通过选取最优的集群中心节点使集群的总通信功率接近实际状况下最优的集群通信功率。
4 结论本文针对目前较为新颖的空间机器人集群通信功率最优问题,提出一种基于数据和数据压缩率预测的集群中心节点选择算法——DCP算法。首先考虑空间机器人对目标的采集数据与空间机器人和目标之间的距离有关,通过建立预测空间机器人的采样数据高斯分布,预测空间机器人未来时刻的数据量。同时根据空间机器人集群中不同空间机器人之间的相对轨迹位置,计算两两之间的数据压缩率,然后根据预测出的数据与数据压缩率计算集群通信功率并求得最优的集群中心节点,使得集群总通信功率最优。实验证明:DCP算法可以有效地预测出未来时刻的最优集群中心节点,并将整个集群的通信功耗与实际最优结果的误差保持在3 % 以下;相比Fix、BC、CC及DC算法,DCP算法可以有效地降低集群的通信功耗,延长空间机器人的活动时间,进而增强集群的整体性能。
| [1] |
孟光, 韩亮亮, 张崇峰. 空间机器人研究进展及技术挑战[J]. 航空学报, 2021, 42(1): 523963. Doi:10.7527/S1000-6893.2020.23963 |
| [2] |
Ding X L, Wang Y C, Wang Y B, et al. A review of structures, verification, and calibration technologies of space robotic systems for on-orbit servicing[J]. Science China Technological Sciences, 2021, 64(3): 462-480. Doi:10.1007/s11431-020-1737-4 |
| [3] |
Oda M, Kibe K, Yamagata F. ETS-Ⅶ, space robot in-orbit experiment satellite[C]//Proceedings of IEEE International Conference on Robotics and Automation. April 22-28, 1996, Minneapolis, MN, USA. IEEE, 2002: 739-744. DOI: 10.1109/ROBOT.1996.503862.
|
| [4] |
Ogilvie A, Allport J, Hannah M, et al. Autonomous robotic operations for on-orbit satellite servicing[C]//SPIE Defense and Security Symposium. Proc SPIE 6958, Sensors and Systems for Space Applications Ⅱ, Orlando, Florida, USA. 2008, 6958: 50-61. DOI: 10.1117/12.784081.
|
| [5] |
刘宏, 蒋再男, 刘业超. 空间机械臂技术发展综述[J]. 载人航天, 2015, 21(5): 435-443. Doi:10.16329/j.cnki.zrht.2015.05.002 |
| [6] |
Li W J, Cheng D Y, Liu X G, et al. On-orbit service (OOS) of spacecraft: a review of engineering developments[J]. Progress in Aerospace Sciences, 2019, 108: 32-120. Doi:10.1016/j.paerosci.2019.01.004 |
| [7] |
Song R, Song X M, Ma Y N, et al. Research on orbit design method for on-orbit service of high orbit spacecraft[C]//2021 IEEE 2nd International Conference on Information Technology, Big Data and Artificial Intelligence (ICIBA). December 17-19, 2021, Chongqing, China. IEEE, 2022: 657-661. DOI: 10.1109/ICIBA52610.2021.9688110.
|
| [8] |
Mark C P, Kamath S. Review of active space debris removal methods[J]. Space Policy, 2019, 47: 194-206. Doi:10.1016/j.spacepol.2018.12.005 |
| [9] |
Koene J. Applied network analysis: a methodological introduction[J]. European Journal of Operational Research, 1984, 17(3): 422-423. Doi:10.1016/0377-2217(84)90146-2 |
| [10] |
Chen D B, Lü L Y, Shang M S, et al. Identifying influential nodes in complex networks[J]. Physica A: Statistical Mechanics and Its Applications, 2012, 391(4): 1777-1787. Doi:10.1016/j.physa.2011.09.017 |
| [11] |
Nie T Y, Guo Z, Zhao K, et al. Using mapping entropy to identify node centrality in complex networks[J]. Physica A: Statistical Mechanics and Its Applications, 2016, 453: 290-297. Doi:10.1016/j.physa.2016.02.009 |
| [12] |
Kitsak M, Gallos L K, Havlin S, et al. Identification of influential spreaders in complex networks[J]. Nature Physics, 2010, 6(11): 888-893. Doi:10.1038/nphys1746 |
| [13] |
周丽娜, 李发旭, 巩云超, 等. 基于K-shell的超网络关键节点识别方法[J]. 复杂系统与复杂性科学, 2021, 18(3): 15-22. Doi:10.13306/j.1672-3813.2021.03.003 |
| [14] |
李钢, 王聿达, 崔蓉. KiC: 一种结合"结构洞"约束值与K壳分解的社交网络关键节点识别算法[J]. 现代情报, 2020, 40(12): 27-35. Doi:10.3969/j.issn.1008-0821.2020.12.003 |
| [15] |
Nardelli E, Proietti G, Widmayer P. Finding the most vital node of a shortest path[M]//Lecture Notes in Computer Science. Berlin, Heidelberg: Springer Berlin Heidelberg, 2001: 278-287. DOI: 10.1007/3-540-44679-6_31.
|
| [16] |
赵星. 信息网络关键节点对之删除判定[J]. 中国图书馆学报, 2018, 44(5): 47-58. Doi:10.13530/j.cnki.jlis.180014 |
| [17] |
Yang Y Z, Yu L, Wang X, et al. A novel method to identify influential nodes in complex networks[J]. International Journal of Modern Physics C, 2020, 31(2): 2050022. Doi:10.1142/s0129183120500229 |
 2024, Vol. 41
2024, Vol. 41 


