随着能源危机问题日趋严重,磁约束受控核聚变技术受到越来越广泛的关注。然而时至今日,该技术仍然面临科学和技术上的诸多难题,偏滤器中的关键部件即面向等离子体材料(plasma facing material, PFM)的选择就是其中之一。在正常运行过程中,PFM通常受到强磁场、高热负荷和高能量中子辐照等极端条件的共同作用[1-3],这些工作条件使得PFM的选择非常有限。金属钨(W)具有高熔点和高热导率等优点,被认为是目前偏滤器中最有前途的材料之一[4],针对其在高能中子辐照时材料内部损伤演化的研究对聚变装置的稳定运行尤为重要。
实验研究已经证实,中子辐照会造成材料的屈服强度[5]、电阻率[6]和热导率[7]等性能的改变。造成这种现象的主要原因是高能中子在材料内部会引发级联碰撞导致材料中的原子发生离位从而产生缺陷。但受客观条件的限制,实验条件下不能很好地揭示辐照后材料内部的缺陷演化和微观机理。并且,导致这种微观结构变化的辐照损伤只持续几个ps[8],在如此小时间尺度上的实验技术存在一定的局限性。
分子动力学(molecular dynamics, MD)方法可以在原子尺度上跟踪粒子的轨迹,被广泛应用于材料辐照损伤的模拟研究。Zhou等[9]采用MD方法模拟了单晶硅(Si)中的辐照缺陷演化过程,分析了温度和初级离位原子(primary knock-on atom, PKA)能量对辐照后缺陷数量的影响,结果表明随着温度和PKA能量的升高,缺陷的峰值数量都有所增加,但是温度对残留在材料内部的缺陷数量的影响可以忽略不计。Beeler等[10]研究了体心立方(body centered cubic, BCC)铁(Fe)在不同类型的应变作用下产生缺陷数量的变化,MD模拟的结果表明,材料存在简单剪切应变时,通过级联碰撞产生的缺陷数量没有发生显著的变化,而拉伸或压缩应变分别会促进或抑制Fe中缺陷的产生。有关W的辐照损伤研究发现,在中子辐照条件下,He气泡更容易从面密度较低的晶面释放[11]。此外,W晶体中间隙He原子的存在会导致辐照过程中缺陷数量的增多[12],这些研究对于理解W作为PFM在辐照条件下的失效机理具有重要意义。
为了更加系统地研究各种条件下的中子辐照对单晶W中缺陷产生的影响,采用MD的方法模拟分析PKA能量、应变以及掺杂原子对产生缺陷数量的影响,此外,针对辐照产生的缺陷,也考察了它们对单晶W拉伸力学性能的影响。
1 模型和方法本文采用MD方法模拟单晶W在不同条件下的辐照损伤过程,势函数选用Juslin等[13]针对W-C-H系统开发的Tersoff多体势。已有研究表明,该势可以很好地描述W-W、W-H和W-C原子之间的相互作用[14-17]。在进行辐照损伤模拟过程中,模拟区域的尺寸必须足够大,以防止高能粒子穿过边界,从而产生不符合物理实际的效果。模拟区域设定为“50a×50a×50a”,其中a=0.316 5 nm为BCC-W的晶格常数。同时,为避免尺寸效应,消除自由边界的影响,在3个方向均采用周期性边界条件。
在模拟过程中:首先,模型在等温等压(normal pressure and temperature,NPT)系综下弛豫50 ps使系统趋于稳定,选用Parrinello-Rahman方法[18]控压并采用Nose-Hoover方法[19]调节温度;然后,选取模型正中心的一个原子为PKA并赋予速度,PKA能量由mv2/2计算得到。PKA原子的初速度方向设定为<1 3 5>,以往的研究表明该方向可以避开过低或过高的离位能量阈值[20]。整个级联碰撞过程采用微正则(micro-canonical ensemble,NVE)系综模拟20 ps。为防止原子速度过大导致模拟崩溃,时间步长需满足原子在每个时间步内移动的距离小于0.005a。此外,对于每一种工况,进行了10次独立的模拟,并将10次模拟结果的平均值作为最终结果。
使用OVITO软件[21]进行原子构型可视化以及后期数据处理。采用Wigner-Seitz方法[22]识别辐照过程中的间隙和空位缺陷,其基本原理是将辐照前系统中的每个原子划分成Voronoi单元,通过观察辐照过程中每个Voronoi单元中的原子数判断是否形成缺陷,当原子数为0时即为空位缺陷,原子数为2时则产生一个间隙原子。
在拉伸模拟中,载荷沿x方向即 < 0 0 1>晶向施加,在每个时间步上按固定应变率(5×108/s)缩放所有原子在x方向的坐标,其他2个方向上压力设置为0 bar。系统的应力由Virial定理[23]计算得到。在拉伸过程中,系统的全局应力每1 ps计算一次,并且在0.1 ps时间范围内进行平均。应变公式为(l-l0)/l0,其中l0和l分别表示模拟盒子长度的初始值和瞬时值。
本工作中所有的MD模拟工作均采用开源软件LAMMPS[24]完成。
2 结果与讨论 2.1 单晶钨的级联碰撞过程图 1所示为3种PKA初始能量条件下,单晶W内部缺陷数量随时间的典型变化规律。从图中可以看到,在辐照的初始阶段,缺陷数量在大约1 ps内迅速增大并达到峰值。图 1中的插图(a)展示了辐照时间为0.52 ps时缺陷的原子构型。为清晰地展示缺陷,隐藏了晶格点上的W原子,图中红色代表间隙缺陷,蓝色代表空位缺陷(2种缺陷的数量相同并组成了Frenkel缺陷对)。随着辐照的持续进行,Frenkel缺陷对的数量逐渐降低然后基本保持稳定,如图 1中的插图(b)所示,此时晶体中只存在极少数的缺陷。事实上,辐照时间超过6 ps后,缺陷的数量和位置几乎不发生改变,这表明体系达到相对稳定的状态,材料产生永久性的损伤。这种变化规律是由于在辐照开始时,内部原子在PKA的作用下发生级联碰撞,当原子的动能无法使其脱离晶格位置产生缺陷时,级联碰撞停止。随后,部分缺陷原子逐渐发生复合,Frenkel缺陷对数量减少,类似的现象在以往的模拟中都有被观察到[9, 25]。

|
Download:
|
| 插图(a)(b)为单晶钨中缺陷的原子构型,温度为300 K,PKA能量为10 keV。 图 1 Frenkel缺陷对数量随时间的变化 Fig. 1 Numbers of Frenkel defect pairs over time | |
本研究共考察7种不同PKA能量(2、4、6、8、10、12、14 keV)下Frenkel缺陷对峰值和残余量的变化,结果如图 2所示。从图中可以看到,缺陷对的数量随PKA能量的增大而增大。这种规律在Pokor等[26]对不锈钢辐照损伤的实验研究中也被发现。PKA能量的提高意味着初始原子有更高的动能与周围的原子碰撞,对材料造成的损伤更严重,使其产生更多的缺陷并且稳定状态下残留的Frenkel缺陷对数目也增多。我们还注意到,随着PKA能量的增加,达到缺陷对峰值需要更多的时间,当PKA能量为2 keV时,缺陷对数量在0.23 ps达到峰值,当PKA能量为14 keV时,则在0.85 ps达到峰值。这是由于较大的PKA能量需要与更多的原子发生级联碰撞来耗散。

|
Download:
|
| 图中误差条为标准差,下同。 图 2 不同PKA能量下Frenkel缺陷对的数量 Fig. 2 Numbers of Frenkel defect pairs at different values of PKA energy | |
作为PFM,高热负荷会在材料内部产生一定的应变场,从而引起晶格畸变。已有研究表明,晶格的变形可以在一定程度上改变杂质原子在晶格内的扩散过程[27-28]。因此,可以预见,外加应变场必定对材料内部的辐照缺陷演化产生一定的影响。
为考察不同应变状态对单晶W中辐照缺陷演化的影响,模拟了4种类型的载荷,分别为:静水载荷、双轴拉伸/压缩、单轴拉伸/压缩和简单剪切。模拟过程中的PKA能量设置为10 keV,温度为300 K。
图 3所示为不同载荷作用下材料内部Frenkel缺陷对的峰值数量和最终残余数量与应变的关系,可以发现,在[-0.01, 0.01]的应变范围内,静水、双轴和单轴载荷都会导致Frenkel缺陷对峰值和残余量的上升。当材料施加静水载荷时,随着应变从-0.01增大到0.01,缺陷对峰值和残余数量分别增加了120% 和55% 左右。双轴载荷使缺陷对峰值和残余量分别增加89% 和44%,而单轴载荷导致缺陷对峰值和残余量分别增加37% 和19%。此外,这3类载荷的影响结果均表现为压缩抑制缺陷的产生,拉伸促进缺陷的产生。不同于前3种载荷,简单剪切会导致缺陷对数量的减少,但是减少的程度相对较低。

|
Download:
|
| 图 3 不同载荷下Frenkel缺陷对的(a)峰值和(b)残余量 Fig. 3 Peak value (a) and survival value (b) of Frenkel defect pairs under different loads | |
总的来说,静水压力对辐照缺陷的影响最大,通过对比4种载荷(静水、双轴、单轴、剪切)可以发现,静水载荷作用下缺陷对的峰值数量和残余数量的改变量最多。另外,从静水载荷作用下的缺陷峰值数量和残余数量与应变的关系曲线(图 3(a)和3(b)中黑色曲线)来看,在应变区间[-0.01, 0.01]内,随着静水应变的增加,曲线的斜率逐渐增加,表明在相同的应变增量下,缺陷对数量的增加速度加剧,进一步说明静水压力的作用越来越显著。
为解释不同载荷影响缺陷数量的机理,采用如下公式计算单晶W中Frenkel缺陷对的形成能
| $ E_{\mathrm{f}}=E_{\text {defect }}-E_{\text {pure }}, $ |
其中:Epure为无缺陷时系统的能量,Edefect是具有相同原子数但包含一个Frenkel缺陷对的系统的能量。本文中,通过在一个“8a×8a×8a”的晶胞中删除一个原子形成空位,同时填充一个间隙原子来引入Frenkel缺陷对,然后采用共轭梯度法最小化系统的能量,从而计算得到Edefect。需要注意的是,空位和间隙原子必须距离足够远,以防止它们的复合。
计算结果如图 4所示。从图中可以看到,所有的形成能Ef均为正值,这表明缺陷的形成是一个吸热的过程。在温度和PKA能量不变的条件下,较低的Frenkel缺陷对形成能意味着结构在级联碰撞过程中更容易产生缺陷,表现为Frenkel缺陷对数量的增多。图 4中的结果表明,单晶W在静水、双轴和单轴载荷作用下,Ef均呈下降的趋势,单轴载荷作用下Ef的降低程度小于静水和双轴载荷,这与图 3中Frenkel缺陷对数量变化的结果一致。此外,注意到系统在简单剪切作用下的Ef几乎没有改变,相对改变量仅有0.5%,这解释了Frenkel缺陷对不会随剪切应变的增加出现明显的变化趋势。

|
Download:
|
| 图 4 不同载荷下Frenkel缺陷对的形成能 Fig. 4 Formation energies of Frenkel defect pairs under different loads | |
上述结果表明,在工程应用中,对结构施加一定的压缩载荷,特别是静水压力,将有助于降低中子辐照损伤,延长材料的服役寿命。
2.3 碳氢对辐照损伤的影响碳(C)和氢(H)是聚变堆环境下常见的2种元素。作为最轻的元素,来自等离子体的H粒子在轰击第一壁材料时很容易扩散进入材料内部[29],引起材料的微观结构变化,从而改变材料的力学性能[30]。C主要来自于石墨第一壁,其在等离子体轰击后很容易发生化学溅射,从而形成C粒子,并随着等离子体沉积到W壁表面[31-32]。截至目前,有关C/H原子对金属W抗辐照性能的研究尚不多见。鉴于此,我们模拟分析了单晶W中掺杂C/H原子后辐照过程中缺陷数量的变化,C/H的浓度范围为0%、1.0%、3.0% 和5.0%。在初始状态下,C/H原子被随机地放置于晶格填隙位置,考虑到部分C/H原子的初始位置可能与晶格处的W原子距离过近并产生巨大的排斥力,首先采用NVE系综弛豫5 000步,同时,将原子在每个时间步中位移的最大距离限制在0.000 1 nm以内,从而获得稳定的掺杂系统。
图 5所示为Frenkel缺陷对的峰值和残余量随C/H浓度的变化曲线。从图中可以看出,随着掺杂浓度的升高,Frenkel缺陷对逐渐增多,这表明C/H原子的引入会促进缺陷的产生。这种现象的产生是由于掺杂原子的存在导致完美W晶格发生了变化,降低了W-W之间的键强[33],从而使得缺陷对数量增加。随着C/H浓度的增加,杂质原子在间隙中逐渐形成团簇,对W晶格的影响程度增大,因此缺陷对数量持续增加。在本文的模拟中,假定C/H原子距离小于0.2 nm时即组成团簇,统计计算后发现,当浓度为1%、3% 和5% 时,体系中H团簇的数量分别为16、150和462个,C团簇的数量分别为13、148和488个。我们进一步统计了在不同的C/H浓度时,形成团簇的原子比例(团簇原子数/原子总数)。如表 1所示,可以看到,团簇关联原子的比例随C/H浓度的增大而升高,考虑到团簇对W原子扩散的阻碍作用更大,因此随着C/H浓度的升高,Frenkel缺陷对的数量也有所增加。

|
Download:
|
| 图 5 不同H/C浓度下Frenkel缺陷对(a)峰值和(b)残余量 Fig. 5 Peak value (a) and survival value (b) of Frenkel defect pairs at different H/C concentrations | |
|
|
表 1 不同C/H浓度下团簇原子比例 Table 1 The proportion of cluster atoms at different C/H concentrations |
从图 5中还可以看出,相同浓度条件下,C原子比H原子对Frenkel缺陷对峰值数量的影响更大。原因在于C原子体积比H原子大得多,进入W晶格后造成的晶格畸变也相对较大,因此使得附近的W原子更容易离开晶格点位从而形成Frenkel缺陷对,最终导致峰值缺陷对数量更多。另一方面,相比于H原子,填隙C原子还会更大程度地阻碍自间隙W原子在晶格内的扩散,从而降低其与空位的复合几率,增大最终的Frenkel缺陷对数量。
为验证上述结论,构建“10a×10a×10a”的单晶W,同时在系统中分别随机放置3% 浓度的C/H原子和5个间隙W原子。系统首先在1 900 K的温度下采用NPT系综弛豫20 ps,然后统计计算了500 ps内W原子的均方根位移(mean squared displacement,MSD)。之所以选择如此高的温度,是为了加快填隙W原子的扩散,从而节省计算时间。自间隙W原子的运动轨迹如图 6(a)所示,从图中可以看出,自间隙W原子的扩散机制有2种,即:在相邻间隙位置之间跃迁和与晶格W原子的位置交换。例如图 6中的1号W原子,从其运动轨迹可以看出,在模拟初期,该原子通过在相邻间隙位置之间跃迁进行扩散,在某一时刻该原子与晶格原子进行交换,不再产生位移。因此,在计算MSD时,不应该只统计初始填隙W原子,而应该考虑系统中所有的W原子。

|
Download:
|
| 图 6 MSD计算结果 Fig. 6 Calulating results of MSD | |
MSD的计算结果如图 6(b)所示。通过对比可以发现,间隙W原子在含有填隙C原子的晶格内的MSD最小,其次是含有填隙H原子的情况和纯W系统,这表明C原子和H原子都在一定程度上降低了W原子的运动速度。同时,相对于H原子而言,C原子的阻碍效应更加明显。这一结论很好地解释了在相同的PKA能量条件下,含有C原子的W晶格中存在更多的辐照缺陷这一现象。
2.4 辐照对单晶W力学性能的影响上述模拟结果表明不同条件的辐照会产生不同数量的Frenkel缺陷对。为考察缺陷对单晶W力学性能的影响,对含有不同浓度Frenkel缺陷对的单晶W进行了单轴拉伸模拟。Frenkel缺陷对通过在单晶W中随机删除一定比例的晶格点W原子,同时随机放置相同数量的填隙W原子来构建。与引入填隙C/H原子时相同,在构建Frenkel缺陷对之后,首先采用NVE系综对系统进行了5 000步的弛豫,同时限制每一步W原子的移动距离不超过0.000 1 nm,使得填隙W原子到达相对稳定的位置;然后使用NPT系综对系统在300 K和0 bar下弛豫20 ps。考虑到删除和填充W原子的过程是完全随机的,在弛豫过程中会出现部分空位和间隙原子重组从而导致Frenkel缺陷对的浓度低于预期值的情况。为获得预期的缺陷对浓度,在弛豫20 ps后重复上述缺陷构建过程,即随机增加空位和自间隙W原子并进行相应的平衡弛豫,如此循环直至弛豫完成后的缺陷数量满足所需要的浓度要求。
图 7给出单晶W在单轴拉伸载荷作用下的应力-应变曲线。图中黑色实线为纯W的应力-应变曲线,可以看到,在应变较小时, 应力与应变呈线性关系,随着拉伸的继续进行,应力和应变在很大范围内表现出明显的非线性特性,这是由于在单晶W中不存在可以发射位错的缺陷,因此需要较大的载荷才能在完美的晶格中产生位错,这一点已在不少文献中得到证实[33-34]。当应变达到某一临界值时,应力突然急速下降,表明位错开始出现并迅速在单晶内滑移。通过拟合应变范围[0, 0.03]内的应力-应变曲线可以得到单晶W沿 < 1 0 0>方向的杨氏模量为355.25 GPa,与实验值355 GPa[35]和文献中的模拟结果353.12 GPa[33]均比较接近,证明了模拟方法的正确性和势函数的可靠性。

|
Download:
|
| 图 7 不同Frenkel缺陷浓度时单晶W的单轴拉伸应力-应变曲线 Fig. 7 Uniaxial tensile stress-strain curves of single crystal W at different Frenkel defect concentrations | |
从图 7还可以看出,在引入Frenkel缺陷对以后,单晶W的力学行为发生了明显的变化。首先,应力-应变曲线随着缺陷对浓度的升高不断整体下降,通过拟合应变范围[0, 0.03]内的数据可以计算出当缺陷对浓度为0.5% 时,杨氏模量为279.4 GPa,相比纯W下降21.35%。这一现象可以理解为缺陷的存在降低了W-W之间的相互作用,从而降低了其刚度。此外,缺陷的存在大大减小了应力-应变曲线中的非线性部分,即减小了屈服应力和应变,特别是屈服应变,即使缺陷浓度仅为0.1%,屈服应变也从纯W的8.2% 下降到5.2%。这是因为Frenkel缺陷对为位错提供了发射源,从而大大降低了位错发射的难度。随着缺陷对浓度的升高,位错源不断增多,屈服应力和应变进一步降低。在Rafique等[36]的实验研究中,他们发现多晶锆(Zr)受到辐照后产生的缺陷也会导致杨氏模量和屈服强度降低。
除杨氏模量和屈服应力、应变受缺陷的影响,单晶W屈服后的力学行为也受到Frenkel缺陷对的影响。从图 7中可以看出,相比于纯W的系统,包含Frenkel缺陷对的晶体在屈服以后的应力应变曲线更加平缓。随着缺陷对浓度的增加,平缓的程度也逐渐增加。这一现象说明位错的滑移受到Frenkel缺陷对的抑制,从而使得塑性变形过程变得更加缓慢。缺陷对浓度越高,位错滑移越困难,因此应力应变曲线更加平缓。
总的来说,辐照产生的Frenkel缺陷对会引起材料力学性的显著退化,对材料的服役寿命有一定影响,在进行结构设计时需要予以考虑。
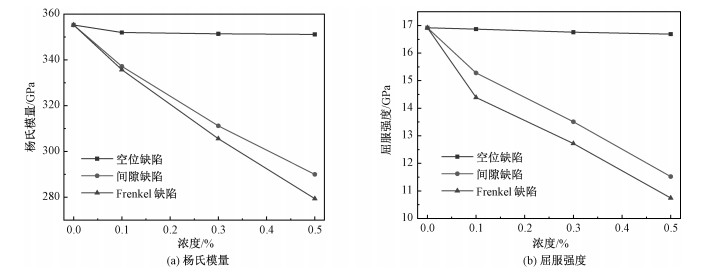
考虑到Frenkel缺陷对由空位和自间隙原子组成,为分别考察这2种缺陷对材料力学性能的影响,分别在单晶W中单独引入不同浓度的空位缺陷和自间隙缺陷,并对包含缺陷的晶格体系进行单轴拉伸模拟,计算杨氏模量和屈服应力,结果如图 8所示。可以看出,随着2种缺陷浓度的升高,单晶W的力学性能均发生一定程度的退化。然而,无论是杨氏模量还是屈服应力,空位缺陷的影响都远小于自间隙原子。计算显示,当间隙缺陷浓度为0.5% 时,单晶W的杨氏模量和屈服强度分别降低18.4% 和31.9%,而在相同浓度的空位缺陷情况下,杨氏模量和屈服应力仅降低1.2% 和1.4%。自间隙原子之所以能够引起弹性模量的显著变化,是因为自间隙原子会在局部产生一定的应力场,该应力场为压应力,使得材料具有膨胀的趋势,因此,在相同的拉伸载荷作用下,材料伸长的位移增加,表现为弹性模量降低,可以预见,当材料受到压缩载荷作用时,将表现为弹性模量增加。这一结论与Li等[37]对单晶Zr和Lin等[38]对单晶Fe的模拟结果完全一致。
|
Download:
|
| 图 8 不同缺陷类型时杨氏模量和屈服强度随缺陷浓度的变化 Fig. 8 Young's modulus and yield strength as a function of defect concentration for different defect types | |
本文采用分子动力学方法对单晶W在中子辐照过程中的缺陷演化进行数值模拟,分析PKA能量、载荷、杂质粒子对缺陷数量,以及辐照缺陷对单晶W力学性能的影响规律。主要结论如下:
1) PKA能量的升高会导致Frenkel缺陷对峰值和残余量的增多,且PKA能量越高,达到缺陷峰值所需的时间越长;
2) 静水载荷、双轴拉伸/压缩、单轴拉伸/压缩都会在一定程度上影响级联碰撞过程中缺陷对的峰值数量和最终数量,压缩和拉伸分别起到抑制和促进缺陷产生的作用,而剪切变形对缺陷对数量的影响较小;
3) C和H原子在W晶格中的滞留会增加辐照缺陷对的数量,且C原子的影响要大于H原子;
4) 辐照产生的Frenkel缺陷对单晶钨的力学性能具有显著影响,材料的弹性模量和屈服应力均随着缺陷对浓度的升高而降低,Frenkel缺陷对一方面可以作为位错源,促进位错的发射,另一方面对位错的运动也具有阻碍作用。
| [1] |
Ushigusa K, Seki M, Suganuma K, et al. Electron cyclotron resonance discharge cleaning by using LHRF system on JT-60U[J]. Fusion Engineering and Design, 1999, 45(2): 137-144. Doi:10.1016/S0920-3796(99)00002-2 |
| [2] |
Federici G, Biel W, Gilbert M R, et al. European DEMO design strategy and consequences for materials[J]. Nuclear Fusion, 2017, 57(9): 092002. Doi:10.1088/1741-4326/57/9/092002 |
| [3] |
Ning R H, Li Y G, Zhou W H, et al. Modeling D retention in W under D ions and neutrons irradiation[J]. Journal of Nuclear Materials, 2012, 430(1/2/3): 20-26. Doi:10.1016/j.jnucmat.2012.06.029 |
| [4] |
Sang C F, Sun J Z, Bonnin X, et al. Modelling of hydrogen isotope retention in the tungsten divertor of EAST during ELMy H-mode[J]. Fusion Engineering and Design, 2014, 89(9/10): 2214-2219. Doi:10.1016/j.fusengdes.2014.01.040 |
| [5] |
Rafique M, Chae S, Kim Y S. Surface, structural and tensile properties of proton beam irradiated zirconium[J]. Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, 2016, 368: 120-128. Doi:10.1016/j.nimb.2015.12.001 |
| [6] |
Hasegawa A, Fukuda M, Nogami S, et al. Neutron irradiation effects on tungsten materials[J]. Fusion Engineering and Design, 2014, 89(7/8): 1568-1572. Doi:10.1016/j.fusengdes.2014.04.035 |
| [7] |
Maruyama T, Harayama M. Neutron-irradiation effect on the thermal-conductivity and dimensional change of graphite materials[J]. Journal of Nuclear Materials, 1992, 195(1/2): 44-50. Doi:10.1016/0022-3115(92)90362-O |
| [8] |
Parashar A, Singh D. Molecular dynamics based study of an irradiated single crystal of niobium[J]. Computational Materials Science, 2017, 131: 48-54. Doi:10.1016/j.commatsci.2017.01.028 |
| [9] |
Zhou Y, Chen B, He H Y, et al. Displacement cascades in monocrystalline silicon: effects of temperature, strain, and PKA energy[J]. Nuclear Technology, 2020, 206(1): 32-39. Doi:10.1080/00295450.2019.1613850 |
| [10] |
Beeler B, Asta M, Hosemann P, et al. Effects of applied strain on radiation damage generation in body-centered cubic iron[J]. Journal of Nuclear Materials, 2015, 459: 159-165. Doi:10.1016/j.jnucmat.2014.12.111 |
| [11] |
Wei G, Ren F, Qin W, et al. Evolution of helium bubbles below different tungsten surfaces under neutron irradiation and non-irradiation conditions[J]. Computational Materials Science, 2018, 148: 242-248. Doi:10.1016/j.commatsci.2018.02.050 |
| [12] |
Yang X D, Deng H Q, Hu N W, et al. Molecular dynamics simulation of the displacement cascades in tungsten with interstitial helium atoms[J]. Fusion Science and Technology, 2014, 66(1): 112-117. Doi:10.13182/FST13-742 |
| [13] |
Juslin N, Erhart P, Traskelin P, et al. Analytical interatomic potential for modeling nonequilibrium processes in the W-C-H system[J]. Journal of Applied Physics, 2005, 98(12): 123520. Doi:10.1063/1.2149492 |
| [14] |
Yang X, Hassanein A. Molecular dynamics simulation of deuterium trapping and bubble formation in tungsten[J]. Journal of Nuclear Materials, 2013, 434(1/2/3): 1-6. Doi:10.1016/j.jnucmat.2012.10.045 |
| [15] |
Wu Y, Krstic P, Zhou F Y, et al. Damage at a tungsten surface induced by impacts of self-atoms[J]. Journal of Nuclear Materials, 2015, 467: 480-487. Doi:10.1016/j.jnucmat.2015.09.049 |
| [16] |
Xiang Y, Zhang B, Shi L Q. Evolution of bubble in tungsten irradiated by deuterium of low energy and high flux by molecular dynamics simulations[J]. Applied Surface Science, 2022, 606: 154715. Doi:10.1016/j.apsusc.2022.154715 |
| [17] |
Yu X G, Gou F J, Li B W, et al. Numerical study of the effect of hydrogen on the crack propagation behavior of single crystal tungsten[J]. Fusion Engineering and Design, 2014, 89(7/8): 1096-1100. Doi:10.1016/j.fusengdes.2013.12.007 |
| [18] |
Parrinello M, Rahman A. Crystal structure and pair potentials: a molecular-dynamics study[J]. Physical Review Letters, 1980, 45(14): 1196-1199. Doi:10.1103/physrevlett.45.1196 |
| [19] |
Hoover W G. Canonical dynamics: equilibrium phase-space distributions[J]. Physical Review A, General Physics, 1985, 31(3): 1695-1697. Doi:10.1103/physreva.31.1695 |
| [20] |
Stoller R E, Odette G R, Wirth B D. Primary damage formation in bcc iron[J]. Journal of Nuclear Materials, 1997, 251: 49-60. Doi:10.1016/S0022-3115(97)00256-0 |
| [21] |
Stukowski A. Visualization and analysis of atomistic simulation data with OVITO-the open visualization tool[J]. Modelling and Simulation in Materials Science and Engineering, 2010, 18(1): 015012. Doi:10.1088/0965-0393/18/1/015012 |
| [22] |
Honeycutt J D, Andersen H C. Molecular dynamics study of melting and freezing of small Lennard-Jones clusters[J]. The Journal of Physical Chemistry, 1987, 91(19): 4950-4963. Doi:10.1021/j100303a014 |
| [23] |
Tsai D H. The virial theorem and stress calculation in molecular dynamics[J]. The Journal of Chemical Physics, 1979, 70(3): 1375-1382. Doi:10.1063/1.437577 |
| [24] |
Plimpton S. Fast parallel algorithms for short-range molecular dynamics[J]. Journal of Computational Physics, 1995, 117(1): 1-19. Doi:10.1006/jcph.1995.1039 |
| [25] |
Park N Y, Kim Y C, Seok H K, et al. Molecular dynamics simulation of irradiation damage in tungsten[J]. Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, 2007, 265(2): 547-552. Doi:10.1016/j.nimb.2007.10.003 |
| [26] |
Pokor C, Brechet Y, Dubuisson P, et al. Irradiation damage in 304 and 316 stainless steels: experimental investigation and modeling. Part I: Evolution of the microstructure[J]. Journal of Nuclear Materials, 2004, 326(1): 19-29. Doi:10.1016/j.jnucmat.2003.11.007 |
| [27] |
Hossain M Z, Marian J. Stress-dependent solute energetics in W-Re alloys from first-principles calculations[J]. Acta Materialia, 2014, 80: 107-117. Doi:10.1016/j.actamat.2014.07.028 |
| [28] |
Li X, Gao C, Xiong X L, et al. Hydrogen diffusion in α-Fe under an applied 3-axis strain: a quantum manifestation[J]. International Journal of Hydrogen Energy, 2015, 40(32): 10340-10345. Doi:10.1016/j.ijhydene.2015.06.089 |
| [29] |
Wang W M, Roth J, Lindig S, et al. Blister formation of tungsten due to ion bombardment[J]. Journal of Nuclear Materials, 2001, 299(2): 124-131. Doi:10.1016/S0022-3115(01)00679-1 |
| [30] |
Zhang T, Chu W Y, Gao K W, et al. Study of correlation between hydrogen-induced stress and hydrogen embrittlement[J]. Materials Science and Engineering: A, 2003, 347(1/2): 291-299. Doi:10.1016/S0921-5093(02)00600-7 |
| [31] |
Aymar R, Team I J C, Home T. Present status and future prospect of the ITER project[J]. Journal of Nuclear Materials, 1998, 258/259/260/261/262/263: 56-64. Doi:10.1016/s0022-3115(98)00354-7 |
| [32] |
T Tanabe, T Ohgo, M Wada, et al. Material mixing on W/C twin limiter in TEXTOR-94[J]. Fusion Engineering and Design, 2000, 49/50: 355-362. Doi:10.1016/S0920-3796(00)00396-3 |
| [33] |
Yu X G, Gou F J, Tian X. Molecular dynamics study of the effect of hydrogen on the mechanical properties of tungsten[J]. Journal of Nuclear Materials, 2013, 441(1/2/3): 324-330. Doi:10.1016/j.jnucmat.2013.06.018 |
| [34] |
Wei W, Yu X G. Molecular dynamics study of the effect of lithium on the tensile behaviors of bcc iron[J]. Materials Today Communications, 2020, 24: 101217. Doi:10.1016/j.mtcomm.2020.101217 |
| [35] |
Cimalla V, Rohlig C C, Pezoldt J, et al. Nanomechanics of single crystalline tungsten nanowires[J]. Journal of Nanomaterials, 2008, 2008: 638947. Doi:10.1155/2008/638947 |
| [36] |
Rafique M, Afzal N, Ahmad R, et al. Mechanical behavior of low-dose neutron-irradiated polycrystalline zirconium[J]. Radiation Effects and Defects in Solids, 2012, 167(4): 289-297. Doi:10.1080/10420150.2011.644552 |
| [37] |
Li Y, Chen H, Chen Y, et al. Point defect effects on tensile strength of α-zirconium studied by molecular dynamics simulations[J]. Nuclear Materials and Energy, 2019, 20: 100683. Doi:10.1016/j.nme.2019.100683 |
| [38] |
Lin P D, Nie J F, Liu M D. Investigation of the effects of point defects on the tensile strength of BCC-Fe using molecular dynamics[J]. Applied Physics A, 2021, 127(7): 565. Doi:10.1007/s00339-021-04720-5 |
 2024, Vol. 41
2024, Vol. 41 


