2. 中国科学院过程工程研究所 中国科学院粉体材料技术重点实验室,北京 100190;
3. 郑州中科新兴产业技术研究院,郑州 450000
2. CAS Key Laboratory of Science and Technology on Particle Materials, Institute of Process Engineering, Chinese Academy of Sciences, Beijing 100190, China;
3. Zhengzhou Institute of Emerging Industrial Technology, Zhengzhou 450000, China
环丙基甲基酮(CPMK)有不同于直链脂肪烃的三元环结构,环丙基的3个碳原子处于同一平面内,C—C键介于单键和双键之间,有类似双键的性质,其C—C—C键角为60°,C—C键长为0.151 nm,化学活性高。由于其特殊的三元环结构,CPMK广泛用于医药中间体[1-6]、高能燃料[7-8]等众多工业领域。在医药领域,特殊的环丙基结构的分子sp3杂化性质的增加,进而增强了药物分子的水溶性,使其具有良好的药代动力学性质[9],更高的生物利用度和更长的作用持续时间。如以CPMK为原料制备的药物匹伐他汀(Pitavastatin)[10]可以降低血胆固醇从而延缓动脉粥样硬化,常用于治疗高脂血症以及高血脂引发的冠心病等。在高能燃料领域,环丙基含有高的张力能,可显著提升碳氢燃料的能量密度,如以CPMK为原料合成的syntin燃料已经应用到火箭推进剂中[8]。
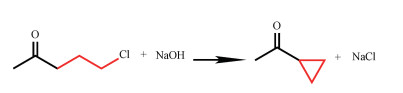
CPMK的合成主要有2条路线。第1条[11]:以乙酰乙酸乙酯和环氧乙烷为原料,制备得到α-乙酰基-γ-丁内酯,并使其在盐酸的环境下开环生成5-氯-2-戊酮(CPE),最后用碱性催化剂处理,环合制得CPMK。第2条[12]:2-甲基呋喃[13-15]作为初始原料,利用Pd/C催化剂加氢开环成5-羟基-2-戊酮,并与盐酸进行氯代反应转化为CPE,最后在氢氧化钠溶液中通过环合反应生成CPMK。这2条路线最后一步(见方案1)都是CPE环化成CPMK,由于CPMK和未反应完全物CPE之间的沸点差异很大,通过简单的精馏就能实现很好的分离。为有效获得环丙基甲基酮的高纯度的产品,需对精馏工艺进行模拟计算,这对CPE与CPMK的物性参数和CPE+CPMK二元体系的汽液相平衡数据提出了更高要求,目前还没有相关数据可用。
|
Download:
|
| 图 方案1 环丙基甲基酮的合成路线 Fig. 方案1 Synthesis routes of CPMK | |
因此,本文系统测定了所得5-氯-2-戊酮和环丙基甲基酮的物性参数,如密度、黏度、摩尔体积、热膨胀系数和表面张力等;对CPE+CPMK二元体系的汽液相平衡(VLE)进行了测定;使用Aspen Plus V11中的多种热力学模型计算相平衡参数,为精馏塔的过程模拟提供了热力学数据。
1 实验部分 1.1 实验试剂5-氯-2-戊酮,分析纯,纯度96%,阿拉丁化学试剂有限公司。环丙基甲基酮,自制,纯度99.8%。无水乙醇,分析纯,纯度大于99.7%,国药集团化学试剂有限公司。
1.2 试剂处理5-氯-2-戊酮:沸点170 ℃,在高温下容易发生聚合,采用减压蒸馏,收集3 kPa下71 ℃的馏分,采用气相色谱归一化法检测纯度98.9%。
1.3 分析方法密度黏度测定: 奥地利DMA 5000M-Lovis 2000 ME密度黏度计,测量精度分别为±1.0×10-3 g ·cm-3和±1.0×10-2 mPa ·s。用注射器将样品直接注入测量室,测温范围为293.15~323.15 K。所有测量均在相同条件下进行3次,取平均值。
表面张力测定:德国克吕士DSA25液滴形状分析仪,测量精度为0.01 mN ·m-1。
汽液相平衡测试:中国浙江中控科教仪器设备有限公司William-Rose汽液相平衡釜,测量精度分别为±0.1 K和±0.1 kPa。
质量分数及纯度的测定:日本岛津GC-2030气相色谱仪,检测器氢火焰离子检测器(FID);气相进样1 μL;进样口温度300 ℃;分流比100 ∶1;柱温程序50 ℃(1 min)→10 ℃/min-120 ℃(1 min)→15 ℃/min-280 ℃(9 min);色谱柱规格为RTX-5, 20 m×20 mm×0.25 μm;以正辛烷为内标物。
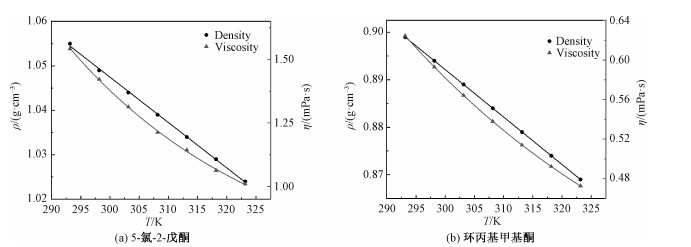
2 实验结果与讨论 2.1 密度和黏度密度和动态黏度[16-18]可以表示物质分子间间隙和作用力的效果,是分子微观作用力在宏观上的表示。本实验采用密度黏度计,在101.3 kPa下测定CPE和CPMK在不同温度下的密度和动态黏度。CPE和CPMK的密度、黏度与温度的函数关系见图 1。其中随着温度的升高,两者的密度都呈线性下降趋势,黏度呈对数下降趋势,这是由于温度升高液体分子动能增加、分子间距变大、范德华作用力减弱所致。同一温度下,CPMK的密度黏度比CPE的都要小,Cl原子的消去减少了分子的密度,而环的生成也拉近分子间的间距,两种因素使CPMK密度减小。与CPE相比,CPMK分子量减少,三元环的生成造成分子链的刚性增强,使流动过程助力和能量也减少,这使得CPMK的黏性下降。
|
Download:
|
| 图 1 密度和黏度随温度的变化关系 Fig. 1 Density and viscosity as a function of temperature | |
图 1的关联方程如下:
| $\rho_{1}=-0.001 \times T+1.35397, \\ \rho_{2}=-0.001 \times T+1.19215, $ | (1) |
| $\eta_{1}=0.0148 \mathrm{e}^{1361.641 / T}, \\ \eta_{2}=0.0307 \mathrm{e}^{882.875 / T} . $ | (2) |
式中:ρ是密度,g ·cm-3;η是动态黏度,mPa ·s;T是温度,K。下标1、2分别代表 5-氯-2-戊酮、环丙基甲基酮。2个方程关联度良好(密度R2=0.999,黏度R2=0.998),可用于计算293.15~323.15 K温度范围内环丙基甲基酮的密度和黏度。
2.2 摩尔体积和热膨胀系数化合物的摩尔体积计算公式如下:
| $ V_{\mathrm{m}} =\frac{M}{\rho} , $ | (3) |
| $ \alpha=\frac{1}{V_{\mathrm{m}}}\left(\frac{\partial V_{\mathrm{m}}}{\partial T}\right)_{P} =-\frac{1}{\rho}\left(\frac{\partial \rho}{\partial T}\right)_{P} . $ | (4) |
热膨胀系数作为化合物几何特性随温度的变化参数,可依据式(4)[19]得到。式中:Vm是摩尔体积,cm3 ·mol-1;M是摩尔质量,g ·mol-1;ρ是密度,g ·cm-3;α是热膨胀系数,10-4 K-1;T是温度,K。
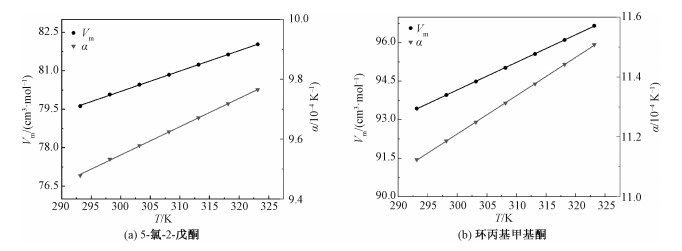
利用获得的密度参数,由式(3)、式(4)可得293.15~323.15 K下CPE和CPMK的摩尔体积和热膨胀系数随温度的变化关系,如图 2所示。在该温度范围内,CPE和CPMK的等压热膨胀系数和摩尔体积随温度的升高呈线性增加,这是由于温度升高,分子间的热运动剧烈,分子间间隙更大导致热膨胀明显。
|
Download:
|
| 图 2 热膨胀系数和摩尔体积随温度变化关系 Fig. 2 Coefficient of thermal expansion and molar volume as a function of temperature | |
对图 2进行线性拟合方程如下:
| $ V_{\mathrm{m} 1}=0.079 T+56.363, V_{\mathrm{m} 2}=0.107 T+61.904, $ | (5) |
| $ \begin{equation*} \alpha_{1}=0.009 T+6.710, \alpha_{2}=0.013 T+7.369 . \end{equation*} $ | (6) |
2个方程得拟合系数为R2=0.999,该方程具有良好的拟合度,可用于293.15~323.15 K温度范围内等压热膨胀系数值的计算。
2.3 表面张力CPMK的表面张力采用悬滴法[20-22]进行测试,在实际测量中,需要灰度分析视频中的图像测定液滴的形状得到形状参数B,根据经验公式计算出与液滴的实际形状参数一致。悬滴法中表面张力由密度差Δρ和修正的参数B计算出,计算公式如下
| $ \begin{equation*} \sigma=\frac{\Delta \rho g D_{e}^{2}}{B} . \end{equation*} $ | (7) |
式中:σ是表面张力,mN ·m-1;Δρ是高密度相与低密度相的密度差,g ·cm-3;De是液滴最宽处直径,即液滴赤道直径,m;B是修正后的形状参数,无量纲;g是重力加速度,m ·s-2。
表 1是在温度293.15 K,压力101.3 kPa下CPE、CPMK的表面张力测量10次的数值。CPE、CPMK的平均表面张力分别为214.57和20.44 mN ·m-1。两者表面张力相差较大的原因在于:CPE中含有O原子和Cl原子,分子内存在极性共价键,当分子的构型由直链转化成环状,同时减弱分子间的相互作用力。
|
|
表 1 5-氯-2-戊酮和环丙基甲基酮的表面张力(293.15 K,101.3 kPa) Table 1 Surface tension data for CPE and CPMK at 293.15 K and 101.3 kPa |
汽液平衡数据实验的测定[23-29]是在一定的压力下,在已稳定的汽液相平衡体系中,分别用取样针取出汽相和液相样品,测定其组成摩尔浓度。利用改进的William-Rose汽液相平衡釜[30],采用循环法,不断调整平衡体系,分别取样后,用岛津气相色谱仪测定液相中难挥发组分CPE和易挥发组分CPMK的样品浓度变化,和汽相中难挥发组分CPE和易挥发组分CPMK的样品浓度变化,得到的汽液平衡数据T-P-xi-yi。在中、低压力中汽液相可视为部分理想体系,即汽相为理想气体混合物,液相为真实溶液,计算活度系数γ。利用Van Laar方程[31]、Wilson方程[32]和NRTL方程[33-34]等对实验数据进行关联拟合,得到该体系的二元交互参数。根据所得的参数,可对该实验结果进行热力学一致性检查。
2.4.1 相平衡数据在常压下,CPE(1)+CPMK(2)二元体系的汽相可近似看作理想气体,液相看作是真实溶液。
| $ \gamma_{1}=\frac{y_{1} P}{x_{1} P_{1}^{0}}, \gamma_{2}=\frac{y_{2} P}{x_{2} P_{2}^{0}} ; $ | (8) |
| $ \ln P^{0}=A_{\mathrm{An}}-\frac{B_{\mathrm{An}}}{T+C_{\mathrm{An}}} . $ | (9) |
式中:x1、x2分别是CPE和CPMK的液相的摩尔分数;y1、y2分别是CPE和CPMK的汽相的摩尔分数;γ1、γ2分别是CPE和CPMK的活度系数;P10、P20分别是CPE和CPMK的饱和蒸汽压;AAn、BAn、CAn分别为Antoine常数,来源于Aspen Plus V11物性数据库。
此时,混合溶液活度系数γi的计算公式可表示为式(8),计算结果见表 2。饱和蒸汽压可用Antione方程计算,见式(9)。在常压下测得CPE(1)+CPMK(2)汽液相平衡实验数据如表 2所示。
|
|
表 2 5-氯-2-戊酮(1)+环丙基甲基酮(2)汽液相平衡数据(101.3 kPa) Table 2 Vapor-liquid phase equilibrium data of CPE(1)+CPMK(2) at 101.3 kPa |
从热力学角度分析,任何体系的汽液相平衡实验数据T-P-xi-yi之间不是独立存在,而是受相律的影响,活度系数可以很好地检验实验数据的可靠程度。
| $ D=100 \times \frac{\int_{0}^{1} \ln \left(\frac{\gamma_{1}}{\gamma_{2}}\right) \mathrm{d} x_{1}}{\int_{0}^{1} \ln \left|\frac{\gamma_{1}}{\gamma_{2}}\right| \mathrm{d} x_{1}}, $ | (10) |
| $J=150 \times \frac{T_{\max }-T_{\min }}{T_{\min }} . $ | (11) |
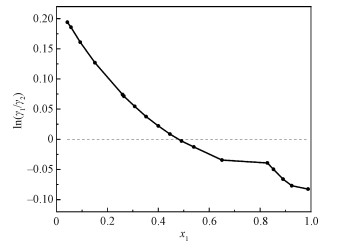
式中D为实验测量得到的汽液相平衡数据,J为某种理论模型或方程计算得到的预测值。Herington[35]提出半经验公式检验热力学一致性,以ln(γ1/γ2)为纵坐标,x1为横坐标,用OriginPro 2022b作图并积分,如图 3所示。由式(10)、式(11)计算D为32.02,J为22.90,D-J=9.12 < 10,符合热力学一致性。
|
Download:
|
| 图 3 5-氯-2-戊酮(1)+环丙基甲基酮(2)的ln(γ1/γ2)-x1关系图 Fig. 3 Plot of ln(γ1/γ2)-x1 of CPE (1) +CPMK (2) | |
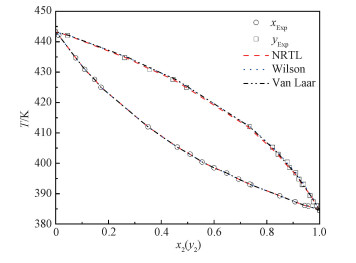
分别用Van Laar、Wilson和NRTL模型在Aspen Plus V11中对实验数据进行关联,得到二元交互参数见表 3。相平衡数据关联结果如图 4所示。3种活度系数模型都可以很好地关联CPE (1)+CPMK (2)体系。3种模型回归所得T-x-y拟合曲线相似,与实验值基本重合。该体系中无共沸点存在,传质推动力大,需塔板数较少的普通精馏就能将两者分离。
|
|
表 3 5-氯-2-戊酮(1)+环丙基甲基酮(2)的二元交互参数与均方根偏差 Table 3 Binary interaction parameters and root mean square deviations for CPE (1) + CPMK (2) |
|
Download:
|
| 图 4 5-氯-2-戊酮(1)+环丙基甲基酮(2)的汽液相平衡图 Fig. 4 Vapor-liquid phase equilibrium diagram of CPE (1)+CPMK (2) | |
Van Laar方程
| $\begin{equation*} \ln \gamma_{i}=\frac{A_{i j}}{\left(1+\frac{A_{i j} x_{i}}{A_{j i} x_{j}}\right)^{2}} \end{equation*}. $ | (12) |
Wilson方程
| $ \begin{equation*} \ln \gamma_{i}=-\ln \left(x_{i}+A_{i j} x_{j}\right)+x_{j}\left(\frac{A_{i j}}{x_{i}+A_{i j} x_{i}}-\frac{A_{j i}}{x_{j}+A_{j i} x_{i}}\right) . \end{equation*} $ | (13) |
NRTL方程
| $ \begin{equation*} \ln \gamma_{i}=x_{j}^{2}\left[\frac{\tau_{j i} G_{j i}^{2}}{\left(x_{i}+x_{j} G_{j i}\right)^{2}}+\frac{\tau_{i j} G_{i j}}{\left(x_{j}+x_{i} G_{i j}\right)^{2}}\right] . \end{equation*} $ | (14) |
式(14)中
式中:xi、xj分别是i组分和j组分的液相的摩尔分数;γi、γj分别是i组分和j组分的活度系数;Aij、Aij、Bij、Bij、C分别是对应模型中的二元交互参数。
| $\operatorname{RMSD}\left(T_{i}\right)=\sqrt{\sum\limits_{i}^{N} \frac{\left(T_{i}^{\text {exp }}-T_{i}^{\text {cal }}\right)^{2}}{N}} , $ | (15) |
| $ \operatorname{RMSD}\left(y_{i}\right)=\sqrt{\sum\limits_{i}^{N} \frac{\left(y_{i}^{\text {exp }}-y_{i}^{\text {cal }}\right)^{2}}{N}} . $ | (16) |
式中:Ti是i组分的平衡时的温度,K;N是实验的取样点数;上标exp、cal分别是实验值和计算值。
在各组回归数据中,温度、汽相摩尔分数偏差最大,对其进行均方根偏差(RMSD)计算,如式(15)、式(16)所示;计算的偏差结果列于表 3中,NRTL模型温度和汽相摩尔分数均方根偏差在3种模型中最小,拟合程度最好。而Van Laar模型中温度和汽相摩尔分数均方根偏差在3种模型中最大,拟合程度最差。但是这3种偏差均不大,这说明所用的3个模型都适合CPE (1) + CPMK (2) 二元体系的关联。
3 结论本文测定了5-氯-2-戊酮在温度293.15~323.15 K的密度为1.024~1.055 g ·cm-3;黏度为1.009~1.543 mPa ·s;摩尔体积为79.621~80.031 cm3 ·mol-1;热膨胀系数为9.479~9.766 g ·cm-3,在293.15 K表面张力为214.57 mN ·m-1。环丙基甲基酮在温度293.15~323.15 K的密度为0.899~ 0.869 g ·cm-3;黏度为0.473~0.625 mPa ·s;摩尔体积为93.437~96.663 cm3 ·mol-1;热膨胀系数为11.123~11.507 g ·cm-3,在293.15 K表面张力为20.44 mN ·m-1。针对5-氯-2-戊酮和环丙基甲基酮二元混合体系,实验测定了其汽液相平衡数据,并利用Van Laar方程、Wilson方程和NRTL方程关联得到其二元交互参数。所得的物性数据、二元汽液相平衡数据及其相关模型拟合方程对环丙基甲基酮的有关化工分离和工业过程设计均具有重要的参考价值。
| [1] |
Umesha B, Basavaraju Y B. Synthesis and pharmacological studies of new pyrazole analogues of podophyllotoxin[J]. Russian Journal of Bioorganic Chemistry, 2014, 40(4): 467-476. Doi:10.1134/S106816201404013X |
| [2] |
Khan G M, Hussain A, Hanif R M. Preparation and evaluation of 5, 9-dimethyl-2-cyclopropyl-2-decanol as a penetration enhancer for drugs through rat skin[J]. Pakistan Journal of Pharmaceutical Sciences, 2011, 24(4): 451-457. |
| [3] |
Butcher K J, Denton S M, Field S E, et al. Convergent asymmetric synthesis of two complex TRPV1 antagonists[J]. Organic Process Research & Development, 2011, 15(5): 1192-1200. Doi:10.1021/op200177b |
| [4] |
Oniciu D C, Pop E, Dasseux J L H, et al. Long hydrocarbon chain diols and diacids with central ether or ketone moieties that favorably alter lipid disorders[J]. Pharmazie, 2006, 61(2): 157-165. |
| [5] |
Hara R, Furukawa T, Kashima H, et al. Enantioselective total synthesis of (+)-taxusin[J]. Journal of the American Chemical Society, 1999, 121(13): 3072-3082. Doi:10.1021/ja984250f |
| [6] |
Burmudžija A Z, Muškinja J M, Kosani Ac'1 M M, et al. Cytotoxic and antimicrobial activity of dehydrozingerone based cyclopropyl derivatives[J]. Chemistry and Biodiversity, 2017, 14(8): e1700077. Doi:10.1002/cbdv.201700077 |
| [7] |
Martel C R. Military jet fuels, 1944-1987[R]. Report number: AFWAL-TR-87-2062. Wright-Patterson Air Force Base, OH.
|
| [8] |
Edwards T. Liquid fuels and propellants for aerospace propulsion: 1903-2003[J]. Journal of Propulsion and Power, 2003, 19(6): 1089-1107. Doi:10.2514/2.6946 |
| [9] |
何笑荣, 邹定, 姜文清, 等. 降血脂新药匹伐他汀[J]. 中国新药杂志, 2005, 14(4): 483-487. Doi:10.3321/j.issn:1003-3734.2005.04.031 |
| [10] |
Mochizuki T, Aoki Y, Yoshikado T, et al. Physiologically-based pharmacokinetic model-based translation of OATP1B-mediated drug-drug interactions from coproporphyrin I to probe drugs[J]. Clinical and Translational Science, 2022, 15(6): 1519-1531. Doi:10.1111/cts.13272 |
| [11] |
杨季秋, 严晞, 廖志新, 等. 环丙基甲基酮和环丙烷羧酸的合成[J]. 化学世界, 1990, 31(8): 356-358. Doi:10.19500/j.cnki.0367-6358.1990.08.008 |
| [12] |
程捷, 程维兹, 胡小健, 等. 环丙基甲基酮的制备方法: CN1994996[P]. 2007-07-11.
|
| [13] |
Chen J J, Sun W X, Wang Y X, et al. Performant Au hydrogenation catalyst cooperated with Cu-doped Al2O3 for selective conversion of furfural to furfuryl alcohol at ambient pressure[J]. Green Energy & Environment, 2021, 6(4): 546-556. Doi:10.1016/j.gee.2020.05.005 |
| [14] |
Dai J H. Synthesis of 2, 5-diformylfuran from renewable carbohydrates and its applications: a review[J]. Green Energy & Environment, 2021, 6(1): 22-32. Doi:10.1016/j.gee.2020.06.013 |
| [15] |
Xu Q, Hu X, Zhang L J, et al. Cross-polymerization between the model furans and phenolics in bio-oil with acid or alkaline catalysts[J]. Green Energy & Environment, 2021, 6(1): 138-149. Doi:10.1016/j.gee.2020.03.009 |
| [16] |
Kuznetsov K I, Skorodumov S V, Granchenko P P. Measurements of the dynamic viscosity and density of KOH solutions at atmospheric pressure[J]. High Temperature, 2020, 58(6): 806-811. Doi:10.1134/S0018151X20060127 |
| [17] |
Ramírez Verduzco L F. Density and viscosity of biodiesel as a function of temperature: Empirical models[J]. Renewable and Sustainable Energy Reviews, 2013, 19: 652-665. Doi:10.1016/j.rser.2012.11.022 |
| [18] |
Li H, Wang H K, Chen X S, et al. Measurement and correlation of densities and viscosities of 11 α-hydroxy-16α, 17α-epoxyprogesterone in chloroform[J]. Russian Journal of Physical Chemistry A, 2012, 86(4): 580-583. Doi:10.1134/s0036024412040127 |
| [19] |
Kuduva S S, Sarma J A R P, Katz A K, et al. Melting-points of the meta- and para-isomers of anisylpinacolone[J]. Journal of Physical Organic Chemistry, 2000, 13(11): 719-728. Doi:10.1002/1099-1395(200011)13:11<719:AID-POC308>3.0.CO;2-2 |
| [20] |
Andreas J M, Hauser E A, Tucker W B. Boundary tension by pendant DROPS1[J]. The Journal of Physical Chemistry, 1938, 42(8): 1001-1019. Doi:10.1021/j100903a002 |
| [21] |
Fordham S. On the calculation of surface tension from measurements of pendant drops[J]. Proceedings of the Royal Society of London Series A Mathematical and Physical Sciences, 1948, 194(1036): 1-16. Doi:10.1098/rspa.1948.0063 |
| [22] |
Yu L M Y, Lu J J, Chan Y W, et al. Constrained sessile drop as a new configuration to measure low surface tension in lung surfactant systems[J]. Journal of Applied Physiology (Bethesda, Md.: 1985), 2004, 97(2): 704-715. Doi:10.1152/japplphysiol.00089.2003 |
| [23] |
Wang X D, Gao Y, Yang J B, et al. Density, viscosity, and vapor-liquid equilibrium data for the binary mixture at atmosphere pressure: cyclopropyl methyl ketone + 2-acetylbutyrolactone, cyclopropyl methyl ketone + 5-chloro-2-pentanone[J]. Journal of Chemical & Engineering Data, 2017, 62(11): 3642-3650. Doi:10.1021/acs.jced.7b00344 |
| [24] |
Królikowska M, Gos N, Skonieczny M. Temperature and composition dependence of the thermodynamic properties of an aqueous solution of 1-ethyl-3-methylimidazolium formate and 1-ethyl-3-methylimidazolium acetate[J]. Journal of Chemical & Engineering Data, 2021, 66(8): 3300-3314. Doi:10.1021/acs.jced.1c00349 |
| [25] |
Houng P, Murakami Y, Shimoyama Y. Flow patterns in microfluidic system of CO2+1-propanol, ethanol, methanol, and hexane binary mixtures at high pressures[J]. Chemical Engineering Journal, 2020, 394: 124891. Doi:10.1016/j.cej.2020.124891 |
| [26] |
Khalifa M, Housam B, Ahmed B. Modeling of the phase behavior of CO2 in water, methanol, ethanol and acetone by different equations of state[J]. Fluid Phase Equilibria, 2018, 469: 9-25. Doi:10.1016/j.fluid.2018.04.006 |
| [27] |
Królikowska M, Grzeszyk K, Skonieczny M, et al. New experimental data on thermodynamic properties of the aqueous solution of N, N-diethyl-N-methylammonium bromide and N, N-diethyl-N-methylammonium methanesulfonate[J]. Journal of Chemical & Engineering Data, 2021, 66(5): 2281-2294. Doi:10.1021/acs.jced.1c00111 |
| [28] |
Jiang X M, Ward T L, van Swol F, et al. Numerical simulation of ethanol-water-NaCl droplet evaporation[J]. Industrial & Engineering Chemistry Research, 2010, 49(12): 5631-5643. Doi:10.1021/ie902042z |
| [29] |
Kariznovi M, Nourozieh H, Abedi J. Vapor-liquid phase equilibria and physical properties measurements for ternary systems (methane + decane + hexadecane)[J]. Journal of Chemical & Engineering Data, 2012, 57(9): 2535-2542. Doi:10.1021/je300482b |
| [30] |
陈建芳. 改进的Rose釜用于测取糠醛-水稀溶液的汽液平衡数据[J]. 广州化工, 1998, 26(4): 43-45. |
| [31] |
Laar J J V. The vapor pressure of binary mixtures[J]. Zeitschrift für Physikalische Chemie, 1910, 72U(1): 723-751. Doi:10.1515/zpch-1910-7236 |
| [32] |
Wilson G M. Vapor-liquid equilibrium. XI. A new expression for the excess free energy of mixing[J]. Journal of the American Chemical Society, 1964, 86(2): 127-130. Doi:10.1021/ja01056a002 |
| [33] |
Reid R C, Prausnitz J M, Poling B E. The properties of gases and liquids[M]. 4th ed. New York: McGraw-Hill, 1987.
|
| [34] |
Voutsas E, Louli V, Boukouvalas C, et al. Thermodynamic property calculations with the universal mixing rule for EoS/GE models: results with the Peng-Robinson EoS and a UNIFAC model[J]. Fluid Phase Equilibria, 2006, 241(1/2): 216-228. Doi:10.1016/j.fluid.2005.12.028 |
| [35] |
Wisniak J. The Herington test for thermodynamic consistency[J]. Industrial & Engineering Chemistry Research, 1994, 33(1): 177-180. Doi:10.1021/ie00025a025 |
 2024, Vol. 41
2024, Vol. 41 


