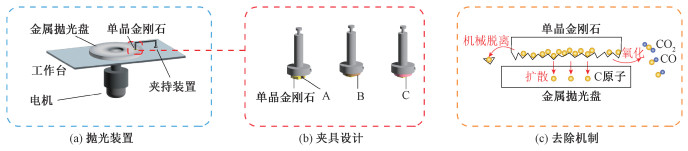
单晶金刚石是自然界硬度、热导率、声速最高的物质,具有优异的综合理化性能[1-3]。在实验室中,人们使用化学气相沉积(chemical vapor deposition,CVD)技术先后制备出40 mm×60 mm[4]和4 inch[5]的人造单晶金刚石,并实现了2 inch人造单晶金刚石的工业化生产[6]。这些成果使得单晶金刚石在精密加工[7]、通道散热[8]、声表面波器件[9]等领域的实际应用越来越成为可能。近来的研究表明,具有色心的单晶金刚石,在量子通讯和量子计算领域也存在巨大的应用潜力[10]。然而,金刚石极高的硬度和优异的理化性能却使其抛光加工非常困难,将表面粗糙度从μm级降低到nm级,往往需要几十到上百小时的抛光时间。在抛光过程中,金刚石又常常发生碎裂,这成为阻碍单晶金刚石高端应用的一个世界性难题[11-13]。因此,人们尝试了各种抛光技术,以期获得高效率和低损耗的金刚石抛光方法。近年来,动态摩擦抛光方法(dynamic friction polishing,DFP)引起人们的广泛关注,因为这种方法具有极高的金刚石去除速率,而且克服了其他抛光方法中存在的“抛光速率受抛光晶面取向影响”的问题[14]。金刚石DFP抛光方法的设备示意图如图 1(a)所示,单晶金刚石在图 1(b)夹具的夹持下,与高速旋转的金属抛光盘紧密接触,通过去除表面的微凸峰来降低粗糙度。Suzuki等[15]、Chen等[13, 16-17]揭示在DFP中金刚石的去除过程为:碳的机械脱离、碳向抛光盘扩散以及碳的氧化,如图 1(c)所示。目前DFP的研究主要集中在获得最高去除速率和最低粗糙度2个方向。Shi等[18]、Jin等[19]通过使用具有较多未配对d壳层电子的合金抛光盘,获得1.5 μm/min的最高去除速率。而Zheng等[20]于2021年使用铸铁抛光盘,在7.4 nm/h的去除速率条件下,获得4.3 nm的表面粗糙度,成为DFP方法报道的最低粗糙度。
|
Download:
|
| 图 1 单晶金刚石的动态摩擦抛光 Fig. 1 Diamond dynamic friction polishing of single crystal diamond | |
但是应该注意到,以往关于DFP的研究主要集中在去除机制的探索,对于影响DFP抛光效果的因素还缺乏系统的研究。另外,大尺寸单晶金刚石是非常昂贵的材料,如何在获得理想的表面粗糙度时保持极小的材料损耗,是DFP这种高去除方法需要考虑的问题。然而,目前这方面的研究还没有报道。因此,本文选取在DFP过程中金刚石的夹持方式、抛光载荷、抛光时间和抛光盘线速率等因素,研究上述因素对抛光效果的影响;并构建K=ΔRa/Δm的抛光评价参量,分析DFP过程中表面粗糙度改善与金刚石材料损耗的关系。
1 试验 1.1 抛光盘与夹持方式本实验中的DFP抛光盘为直径30 cm的铸铁盘,由最大功率为1 kW的电机带动,最大工作转速为2 880 r/min。待抛光的单晶金刚石样品的夹持方式有3种,其中A方式是钻饰加工行业通用的夹持方式,即使用硬度为HRC60的碳素钢对样品进行卡钳式固定;B和C方式是自行设计的夹持方式,B方式使用固化后硬度为HRC54.5的热固酚醛树脂对样品进行镶嵌式固定,C方式使用固化后硬度为HRC50的磷酸-氧化铜双组份无机固化剂对样品进行粘接式固定。这3种夹持方式均可实现金刚石的抛光面与抛光盘的高副接触,使抛光方向垂直于抛光面。
1.2 样品和抛光方向待抛光的单晶金刚石样品为5 mm×5 mm×1 mm规格的高温高压(HTHP)Ib型(400)面的晶片,其表面覆盖有化学气相沉积单晶金刚石(厚度不大于100 μm),CVD单晶金刚石的制备参数见文献[3]。每次抛光前,将样品分别在无水乙醇和去离子水中超声清洗10 min,去除表面油污和杂质。抛光方向为 < 100>,即垂直于样品表面。
1.3 表征方法采用O6223-01型螺旋测微计测量样品的厚度。采用日立SU8010扫描电子显微镜(scanning electron microscope, SEM)观察抛光前后样品的表面形貌。采用威尔量仪SPR2000粗糙度轮廓仪测量样品表面粗糙度,测量长度为2 mm、评价范围为±400 μm,每个样品测量3次并取平均值。采用NT-MDT原子力显微镜(atomic force microscope, AFM)观察样品的表面形貌并测量表面粗糙度,测量区域与轮廓仪一致,测量范围为10 μm×10 μm,采样分辨率256×256,每个样品测量3次并取平均值。采用日本理学Ultima Ⅳ型X射线衍射仪(X-ray diffractomer,XRD)对样品晶体结构进行表征。
2 结果与讨论 2.1 抛光载荷、抛光时间和抛光盘线速率对抛光结果的影响使用表 1中3号抛光参数和夹持方式,对1~3号样品进行抛光。抛光前后样品的SEM表面形貌如图 2所示,从中可见,经抛光后样品表面衬度均匀,没有抛光前衬度分区的情况,说明样品表面变得平整光滑。
|
|
表 1 单晶金刚石抛光加工的工艺参数 Table 1 Process parameters of single crystal diamond polishing processes |

|
Download:
|
| 图 2 扫描电子显微镜下抛光前后样品的表面形貌 Fig. 2 Surface morphology of each sample before and after polishing under scanning electron microscope | |
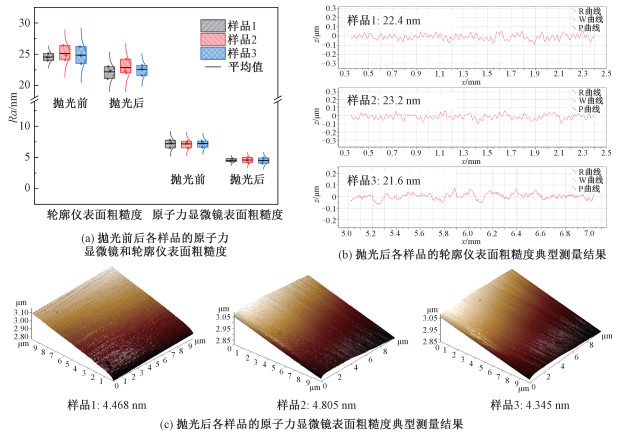
图 3(a)是分别采用轮廓仪和AFM测量的抛光前后各样品的表面粗糙度,图 3(b)是典型的轮廓仪测量结果,图 3(c)是典型的AFM测量结果。图 3(a)中抛光后各试样的Ra平均值分别为:0.022 3、0.023 4和0.021 7 μm(轮廓仪粗糙度)及4.540、4.918和4.247 nm(AFM粗糙度)。因此,根据抛光时间和表 2中对应的样品原始Ra,可以计算出各试样的去除速率分别为:14.4、15.0、13.2 nm/h(轮廓仪数据),以及16.9、16.4、14.1 nm/h(AFM数据)。由此可见,在抛光参数相同时,利用轮廓仪测量的数据与AFM测量的数据获得的去除速率数值相近。本次实验采用AFM测得的表面粗糙度数值与文献[20]所报道的4.3 nm结果相近,但是去除速率却是文献[20]报道速率的2倍。值得注意的是,虽然测量的样品区域是一致的,但是,使用轮廓仪测量得到的粗糙度数值会比使用AFM测量得到的粗糙度数值高出1个数量级。这是由于轮廓仪测量面积的尺度为μm×mm,远远大于AFM的μm×μm尺度,这会放大样品平坦度对粗糙度的影响,使表面粗糙度的数值变大。AFM是一种表面形貌高精度表征设备,价格昂贵、表征耗时长、面积尺度局限在μm×μm级别,不适于全尺寸地测量大面积样品的表面粗糙度。而轮廓仪是当前工业界通用的测量工件表面粗糙度的成型设备,价格相对低廉、表征耗时短,表征精度在nm和μm级别,测量面积尺度甚至可达μm×cm,适合于全尺寸地进行大面积样品的表面粗糙度的测量。基于上述认识,以及本次实验中使用轮廓仪和AFM表征的去除速率数值相近,因此,在后续实验中,都采用轮廓仪来测量样品的粗糙度。
|
Download:
|
| 图 3 表面粗糙度 Fig. 3 Surface roughness | |
|
|
表 2 单晶金刚石样品的原始参数 Table 2 Primitive parameters of single crystal diamond samples |
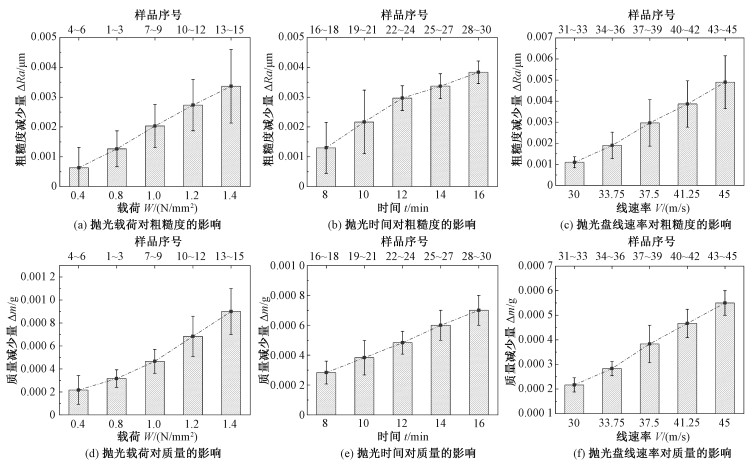
按照表 1中1、2、4~15号抛光参数和夹持方式,对4~45号样品进行抛光,每个参数下使用3个样品。抛光参数对样品表面粗糙度和质量损耗的影响结果汇总于图 4。从图 4(a)~4(c)中可以看到,各个样品的粗糙度变化量ΔRa随着载荷、抛光时间以及抛光盘线速率的增大而增大,这表明增大抛光载荷、加长抛光时间以及增大抛光盘线速率有利于降低样品的表面粗糙度。增大抛光载荷使金刚石与抛光盘有效接触面积变大,摩擦作用显著,金刚石表面微凸峰在机械剪切作用下能快速脱离,表面迅速平坦化;增大抛光盘线速率使接触界面的温度更高,不仅加剧金刚石向非金刚石相的转变和氧化过程,还促使碳原子向铸铁抛光盘中扩散的速度加快;加长抛光时间,则碳的扩散、氧化以及机械脱离过程进行得更为充分[13-14]。从图 4(d)~4(f)中也可见,样品的质量损耗Δm随着载荷、抛光时间以及抛光盘线速率的增大而增大,这与ΔRa的变化相似。
|
Download:
|
| 图 4 不同抛光参数对抛光效果的影响 Fig. 4 Influence of polishing parameters on the polished samples | |
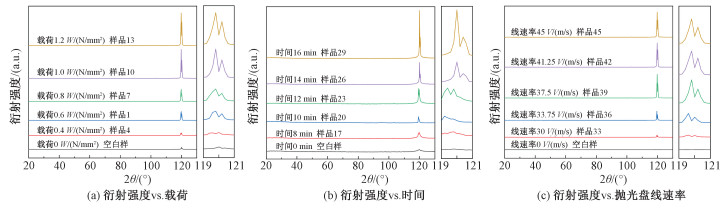
采用XRD方法,对比空白样的晶面衍射强度,考察各抛光参数对晶体抛光面的影响,结果见图 5。其中空白试样是没有抛光的原始样品,因为CVD单晶制备工艺相同,因此,取空白样的XRD结果为参照。图 5中位于119.5°附近的衍射峰对应于金刚石(400)晶面。比照空白样,各抛光试样的(400)衍射峰强度都得到了增强,说明晶体 < 100>取向得到加强,没有发生因抛光面倾斜而导致的抛光面转换。而且增大载荷、延长抛光时间以及增大抛光盘线速率,可以进一步优化晶体的 < 100>取向。
|
Download:
|
| 图 5 抛光样品的X射线衍射结果 Fig. 5 X-ray diffraction results of polished samples | |
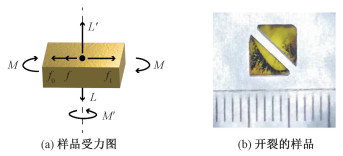
对于A夹持方式,考虑如图 6(a)所示的受力状态。由于卡钳式夹具固定的金刚石与地面相对静止,可认为作用在金刚石上的力为平衡力系,即满足
| $ \begin{gathered} L=L^{\prime} , \end{gathered} $ | (1) |
| $ f_1=f_0+f, $ | (2) |
| $ M=M^{\prime}. $ | (3) |
|
Download:
|
| 图 6 A方式下样品受力图和开裂的样品 Fig. 6 Sample force diagram and cracked sample under A clamping type | |
本次实验的最大电机功率P为1 kW,工作转数n最高为2 880 r/min,则金刚石所受约束力偶M为
| $ M=9\;550 \times \frac{P}{n}=9\;550 \times \frac{1}{2\;880}=3.31 {\mathrm{~N}} \cdot {\mathrm{m}}. $ | (4) |
因此,剪切力Fs为
| $ F_{{\mathrm{s}}}=\frac{M}{l}=\frac{3.31}{0.002\;5}=1\;324 {\mathrm{~N}}. $ | (5) |
所以,切应力τ为
| $ \begin{aligned} & \tau=\frac{F_{{\mathrm{s}}}}{A_{{\mathrm{s}}}}=\frac{1\;324}{0.005 \times 0.001}= \\ & 2.65 \times 10^8 {\mathrm{~Pa}}=265\; {\mathrm{MPa}}. \end{aligned} $ | (6) |
金刚石属于脆性材料,其剪切强度σb为350 MPa,安全系数nb取2.5~3.0,则许用应力[σ]为
| $ [\sigma]=\frac{\sigma_{{\mathrm{b}}}}{n_{{\mathrm{b}}}}=\frac{350}{2.75}=127 \;{\mathrm{MPa}}<\tau. $ | (7) |
可以看出,对于A夹持方式,存在施加于金刚石上的切应力超出许用应力的状态,有可能导致金刚石碎裂。在实验中也确实观察到样品沿(110)面发生穿晶断裂的情况,如图 6(b)所示。因此,另行设计B和C夹持方式,使用低硬度可塑变材料,改善金刚石的受力状态。在目前所进行的实验中,尚未发现样品开裂的情况,并且抛光方向稳定。
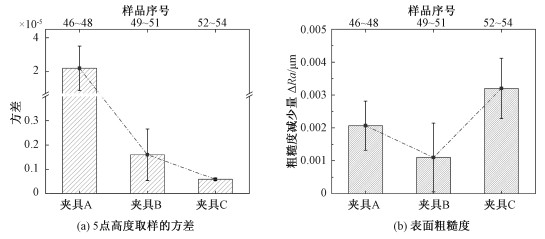
同时比较A、B、C 3种夹持方式对样品表面轮廓和粗糙度的影响。表面轮廓的测量主要根据GB/T 11337—2004平面度误差检测标准,采用在各金刚石样品中心与四角5个点测量高度,然后计算高度方差的方法;使用46~54号样品,采用表 1中的16~18号参数,进行夹持方式对粗糙度影响的研究,结果汇总在图 7中。由图 7(a)可见,样品5点高度方差按A>B>C顺序排列。样品的高度方差小,意味着抛光后样品厚度落差小,斜面少,说明B、C方式较A方式而言,可以获得更平坦的表面。不同夹持方式下表面粗糙度变化如图 7(b)所示,可见,样品的去除速率按C>A>B的顺序排列,C方式可获得的最快去除速率为25.2 nm/h。
|
Download:
|
| 图 7 不同夹持方式对样品表面状态的影响 Fig. 7 The influence of clamping types on the surface state of the samples | |
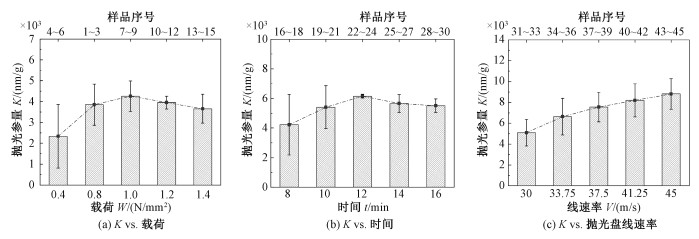
图 4的结果表明,在DFP过程中,样品表面粗糙度得到改善的同时,样品的质量也在减少。因此,构建一个抛光参量K,定义为单晶金刚石粗糙度变化量和质量变化量的比值,即:K=ΔRa/Δm,来研究DFP过程中单晶金刚石表面粗糙度变化与质量变化的比率,其结果如图 8所示。
|
Download:
|
| 图 8 A夹持方式下不同抛光参数对K值的影响 Fig. 8 K values depending on polishing parameters by A clamping type | |
从图 8可以看出,随抛光盘线速率的增加,3个样品的K值都增大,这说明抛光盘的线速率可以在显著降低表面粗糙度的同时,避免样品质量的大量损失。抛光载荷和延长抛光时间对K的影响较为复杂,3个样品都呈现出先增大后减小的趋势,表明DFP的抛光过程应该包含2个阶段:第1阶段为表面粗糙度降低阶段,以粗糙度改善为主。当表面粗糙度降低到一定程度后,转入第2阶段;第2阶段将大量消耗样品质量,为质量损耗为主的阶段,这时K值会减小。通过K值的变化,有理由相信,抛光载荷和抛光时间应该进行合理控制,一味增加两者,虽然表面粗糙度得到改善,但是材料的损失会增大,带来成本上的增加。
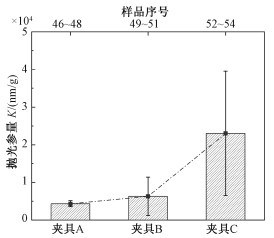
根据试样46~54的抛光结果,考察不同夹持方式对K值的影响,结果如图 9所示。从中可见,采用相同抛光参数时,使用C类粘接方式可以获得较大的K值。这是由于粘接金刚石的粘接剂硬度远小于金刚石,使金刚石在晶体自范性的作用下,更容易调整状态,实现受力晶向保持不变,从而能够减少晶体的质量损耗。另一方面,粘接方式可以使金刚石更容易与夹具端面保持平行,在DFP过程中,能够均匀受力,使得摩擦副的消峰效果显著,即:表面粗糙度的改善明显,而质量消耗却不大。
|
Download:
|
| 图 9 不同夹持方式对K值的影响 Fig. 9 Influence of different clamping types on K values | |
1) 增大抛光载荷、抛光时间和抛光盘线速率,都会增大样品的质量损耗和降低表面粗糙度,并提升金刚石(400)晶面的X-ray衍射强度。
2) 在3种金刚石抛光夹持方式中,样品的去除速率按“粘接式>卡钳式>镶嵌式”的顺序排列,样品厚度的高度方差按“粘接式 < 镶嵌式 < 卡钳式”的顺序排列。
3) 定义了参数K=ΔRa/Δm,根据K值的变化,可将DFP过程划分为粗糙度改善阶段和质量损耗阶段。
4) 提高抛光盘线速率可获得单调增高的K值;而抛光载荷和抛光时间对K值的影响较为复杂,应在抛光过程中对这2个参数进行合理控制,避免增加样品的质量损耗。
| [1] |
Rani D, Opaluch O R, Neu E. Recent advances in single crystal diamond device fabrication for photonics, sensing and nanomechanics[J]. Micromachines, 2020, 12(1): 36. Doi:10.3390/mi12010036 |
| [2] |
Wang Y F, Wang W, Wei J J, et al. Electrochemical route to bio-compatible fluorine-terminated diamond surface[J]. Carbon, 2021, 176: 83-87. Doi:10.1016/j.carbon.2021.01.017 |
| [3] |
Li J J, Li B, Zuo Y G, et al. Application of dual radio frequency inductive coupled plasma into CVD diamond growth[J]. Vacuum, 2018, 154: 174-176. Doi:10.1016/j.vacuum.2018.04.054 |
| [4] |
Yamada H, Chayahara A, Mokuno Y, et al. A 2-in. mosaic wafer made of a single-crystal diamond[J]. Applied Physics Letters, 2014, 104(10): 102110. Doi:10.1063/1.4868720 |
| [5] |
Schreck M, Gsell S, Brescia R, et al. Ion bombardment induced buried lateral growth: the key mechanism for the synthesis of single crystal diamond wafers[J]. Scientific Reports, 2017, 7: 44462. Doi:10.1038/srep44462 |
| [6] |
吕反修, 李成明. 我国化学气相沉积(CVD)金刚石膜研究三十年[J]. 人工晶体学报, 2022, 51(5): 753-758. Doi:10.16553/j.cnki.issn1000-985x.2022.05.005 |
| [7] |
Hou P Y, Zhou M, Zhang H J. Thermal behavior of single-crystal diamonds catalyzed by titanium alloy at elevated temperature[J]. Applied Sciences, 2020, 10(13): 4651. Doi:10.3390/app10134651 |
| [8] |
李小波, 唐大伟, 祝捷. 纳米金刚石颗粒导热系数的分子动力学研究[J]. 中国科学院研究生院学报, 2008, 25(5): 598-601. Doi:10.7523/j.issn.2095-6134.2008.5.004 |
| [9] |
Golter D A, Oo T, Amezcua M, et al. Optomechanical quantum control of a nitrogen-vacancy center in diamond[J]. Physical Review Letters, 2016, 116(14): 143602. Doi:10.1103/PhysRevLett.116.143602 |
| [10] |
Turunen M, Brotons-Gisbert M, Dai Y Y, et al. Quantum photonics with layered 2D materials[J]. Nature Reviews Physics, 2022, 4(4): 219-236. Doi:10.1038/s42254-021-00408-0 |
| [11] |
Feng H B, Chen Y Q, Zhang L C. Polishing of CVD diamond wafers and films[J]. Key Engineering Materials, 2012, 531/532: 373-376. Doi:10.4028/www.scientific.net/kem.531-532.373 |
| [12] |
温海浪, 肖平, 陆静. 大尺寸单晶金刚石衬底抛光技术研究现状与展望[J]. 机械工程学报, 2021, 57(22): 157-171. Doi:10.3901/JME.2021.22.157 |
| [13] |
Chen Y, Zhang L C, Tang F. Surface integrity of PCD composites generated by dynamic friction polishing: effect of processing conditions[J]. Diamond and Related Materials, 2012, 26(6): 25-31. Doi:10.1016/j.diamond.2012.04.002 |
| [14] |
Luo H, Ajmal K M, Liu W, et al. Polishing and planarization of single crystal diamonds: state of the art and perspectives[J]. International Journal of Extreme Manufacturing, 2021, 3(2): 44-91. Doi:10.1088/2631-7990/abe915 |
| [15] |
Suzuki K, Iwai M, Uematsu T, et al. Material removal mechanism in dynamic friction polishing of diamond[J]. Key Engineering Materials, 2003, 238-239(3): 235-240. Doi:10.4028/www.scientific.net/kem.238-239.235 |
| [16] |
Chen Y, Zhang L C, Arsecularatne J A. Polishing of polycrystalline diamond by the technique of dynamic friction. Part 2:Material removal mechanism[J]. International Journal of Machine Tools and Manufacture, 2007, 47(10): 1615-1624. Doi:10.1016/j.ijmachtools.2006.11.003 |
| [17] |
Chen Y Q, Zhang L C. Fast polishing of single crystal diamond[J]. Advanced Materials Research, 2010, 97-101(6): 4096-4099. Doi:10.4028/www.scientific.net/AMR.97-101.4096 |
| [18] |
Shi S J, Jin Z J, Zhong X H, et al. Processing and mechanism of dynamic friction polishing diamond using manganese-based alloy[J]. Materials and Manufacturing Processes, 2015, 30(5): 654-660. Doi:10.1080/10426914.2014.952033 |
| [19] |
Jin Z J, Shi S J, Lin J Z, et al. Preparation and performance of dynamic friction polishing plate for diamond film[J]. Materials and Manufacturing Processes, 2014, 29(1): 20-26. Doi:10.1080/10426914.2013.852219 |
| [20] |
Zheng Y T, Cumont A E L, Bai M J, et al. Smoothing of single crystal diamond by high-speed three-dimensional dynamic friction polishing: optimization and surface bonds evolution mechanism[J]. International Journal of Refractory Metals and Hard Materials, 2021, 96: 105472. Doi:10.1016/j.ijrmhm.2021.105472 |
 2024, Vol. 41
2024, Vol. 41 


