2. 中国科学院空天信息创新研究院,北京 100094
2. Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing 100094, China
激光扫描仪具有无接触、抗噪强、精度高等优点,被广泛应用于逆向工程、数控加工等领域。高端商业扫描仪性能优越但是售价昂贵, 国外产品还会限购; 价格相对便宜的扫描仪精度低、功能少。而且一般扫描系统只提供离散的点云高度数据, 不提供重构和测地距离等功能, 或需要另行购买功能包。因此, 我们希望以相对经济的成本, 配合适用的算法改进, 得到精度较高的几何重构、测量系统。
激光扫描仪向待扫描物体发射激光, 然后通过相机等传感器采集图像信息, 利用图像处理和激光三角法[1]从图像中提取激光位置, 根据标定好的相机参数, 由激光的偏移程度推断得到扫描物体的高度信息。针对激光测距的研究主要分为两类, 分别为设计激光扫描仪系统和设计采集图像处理算法提取激光信息。设计激光扫描仪系统主要是从硬件方面入手提高扫描质量, 文献[2]将整个扫描系统分为6个模块, 实现了整体的扫描过程; 文献[3]通过将机械臂与激光扫描仪相结合, 实现了对复杂物体表面的扫描, 利用机械臂的重复实验的稳定性提高了标定过程的精度。设计采集图像处理算法的工作主要从算法方面提高采集精度, 文献[4]将霍夫变换与直线拟合相结合, 提出了快速在图片上检测激光线的算法; 文献[5]使用finite impulse response滤波方法, 在去噪的同时提取激光中线, 该算法可以在较低信噪比的情况下得到较好的结果, 但是计算相对复杂。当激光测量金属物体的深度时, 由于激光照射在金属上容易产生大量反射, 造成相机采集到的图像里存在光斑, 影响激光位置的提取。工业中一般采取对金属表面处理的方法, 如喷涂反光漆、消除镜面反射。但是这需要处理待测量物体, 失去了非接触式测量的便捷性、精确性。
深度数据获取及处理之后需要做几何重构, 这也是图形学、虚拟现实等方向的共性问题。通过几何重构方法, 将点云数据转化为网格数据, 常见的重建算法可以分为显式重建与隐式重建两种; 显式重建算法包括: 滚球法[6]、power crust算法[7]等; 隐式方法包括泊松重建[8]、多层单元剖分算法[9]、径向基函数算法[10]等。近年来随着智能方法的发展, 出现了很多基于深度学习的重建算法, AtlasNet[11]通过神经网络学习一个映射函数, 将模板顶点直接映射到三维点云从而生成网格数据。DeepSDF[12]学习点云的符号距离函数, 最后通过marching cubes算法[13]生成网格。Gropp等[14]在DeepSDF的基础上引入Eikonal term, 从而提高了重建的几何细节。但如何实现曲面全局光滑性又保证局部尖锐特征仍然是共性问题。
测地线距离近年来被广泛关注, 测地线首先可以作为评价标准, 衡量物体扫描重建的精度, 其次测地线可被用来进行曲面分片[15-16]、曲面编辑[17]、路径规划[18]、几何处理[19]等操作, 这些操作在模型加工、模型设计等下游任务中发挥着重要作用。但是这些方法的理解与实现需要一定的数学与计算机专业知识, 一般的扫描仪仅能提供点云数据, 无法提供网格模型, 也无法进行网格上的测地线距离测量, 如果要得到相应的结果, 需要进一步进行后续处理。
鉴于上述讨论, 本文将搭建经济型无接触几何测量系统。首先以相对便宜的价格搭建了一台具有较高精度的3D激光扫描仪, 并根据扫描获取的点云数据, 通过数据处理和网格重构实现几何重建, 实现了欧式距离测量和常规扫描仪不具备的测地线距离测量功能。
1 自建激光扫描仪本节依据激光三角法原理搭建硬件扫描系统, 并给出自建平台的激光测距处理流程。
1.1 硬件平台搭建激光三角法是将线激光照射在物体表面, 由于物体的高度差异, 激光条纹会产生波动, 通过相机对图像进行采集并计算出激光条纹对应的像素偏移量, 最后由偏移量来估计物体高度的方法。激光三角法分为直射式与斜射式, 一般来说, 斜射式激光三角法激光条纹比直射式激光条纹宽, 光强分布不均匀, 实际测量中对反光较为敏感。而直射式三角法激光光强集中, 可以有效减少环境光的影响。因此, 我们采用的是直射式激光三角法搭建仪器。
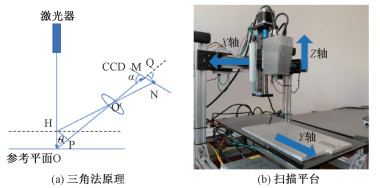
直射式激光三角法原理如图 1(a)所示。其中O′代表镜头光心, 激光垂直打在参考平面的O点, 在相机中成像为点M, 假设待测物体放在参考平面上, 激光点位置由O变为H, 由于激光发生了偏折, 相应图像中激光成的像也由M变为N。令HO=h, MN=Δx, 过H、N分别做OO′的垂线, 垂足为P、Q, 易知ΔHPO′~ΔQNO′, 就能得到对应高度h与像素位移Δx的函数关系如下
| $ h=\frac{\mathrm{OO}^{\prime} \times \Delta x \times \sin \alpha}{\mathrm{O}^{\prime} \mathrm{M} \times \sin \theta+\Delta x \times \sin (\theta+\alpha)}. $ | (1) |
|
Download:
|
| 图 1 三角法原理与自建扫描仪 Fig. 1 Triangulation principle and self-built scanner | |
式(1)在参数全部确定情况下, 可通过激光在图像中像素的偏移得到待测物体的高度信息。
搭建的平台如图 1(b)所示: 由1个HS激光发射器、1个大恒图像MER2-G系列相机、1个移动平台组成。移动平台由3个GX40步进电机组成的三轴系统自搭建而成; 可以控制待测物体在XY平面自由移动, 控制激光发射器和相机沿X、Z轴运动。一般在使用时固定X轴不动, 将相机沿Z轴调整到合适高度, 移动平台让待测物体沿Y轴运动, 整个物体通过激光测距仪的扫描。
1.2 总体流程我们的激光扫描仪可以将图像数据转化为点云数据, 具体框架如算法1所示。
算法1: 图像到点云算法流程
输入: 扫描物体得到的一系列图像, I;
输出: 扫描物体的高精度三维点云数据, P;
1 For对扫描得到的每一张图像Ii do
2 首先对Ii进行图像去噪;
3 对去噪后的图像提取激光中心线;
4 利用标定得到的公式h=f(Δx)计算对应中心线上的高度信息;
5 使用样条拟合对得到的高度线条拟合并保存;
6 end For
7 根据扫描仪器的运动速度等信息,恢复出对应的三维点云P;
8 Return P。
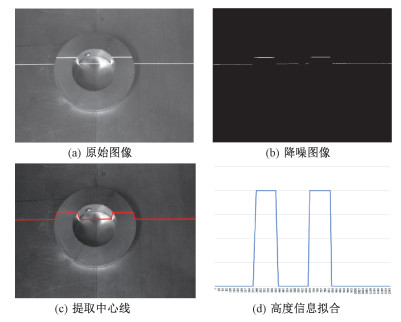
图 2展示激光测距过程中一帧图像信息的高度恢复流程结果。对采集得到的原始图像数据(图 2(a))使用均值滤波器平滑噪声(图 2(b))。采用2.2.1节中的算法, 利用连通域处理激光的物体表面反光, 进而使用灰度重心法提取激光线的坐标, 得到激光线的位置(图 2(c))。最后根据激光在图像中的偏移量计算物体的实际高度, 使用样条方法拟合曲线, 得到最终结果(图 2(d))。
|
Download:
|
| 图 2 图像到点云算法流程 Fig. 2 Flow from image to point cloud algorithm | |
为了得到准确的图像中激光像素偏移与实际高度的对应关系, 需要已知式(1)中的4个参数, 而这些参数和物距、像距、夹角有关, 很难从仪器中获得, 因此需要对公式进行标定。可以将式(1)看作
| $ \frac{1}{h}=k \frac{1}{\Delta x}+b. $ | (2) |
其中:
不同的拟合方法可能会带来不同的影响, 我们主要比较了不同形式的参数拟合方法对结果的影响。对采集到的数据用3种方式进行拟合, 第1种是以
从采集的图像信息提取扫描物体的高度信息, 主要包括两步: 图像去噪、激光中线提取。在实际扫描过程中, 采集到的图像数据难免会受到噪声的影响, 且当扫描金属物体时, 激光会产生镜面反射, 形成大块光斑, 不利于激光中线的提取。因此, 设计了专门的算法用来处理高反光的物体;另外,准确地提取激光中线, 可以有效提高测量精度。
2.2.1 去噪算法采用滤波器与连通域结合的方法对高反光物体噪声进行处理, 详细流程参见算法2。
算法2: 针对高反光物体的去噪算法
输入: 采集的待处理的图像, I;
输出: 处理过后的图像, Inew;
1 对图像I做二值化处理, 并统计每一列非0元素个数,找到众数m
2 对图像I每一列进行处理, 对一列中连续非0区域个数进行排序;
3 将这一列中的非0元素个数明显大于众数m与明显小于众数m的区域置0;
4 将上述处理后的图片与滤波器[1, 1, 1;1, 1, 1;1, 1, 1]进行卷积;
5 对卷积后小于给定阈值的点置0,得到最后的图像Inew;
6 Return Inew。
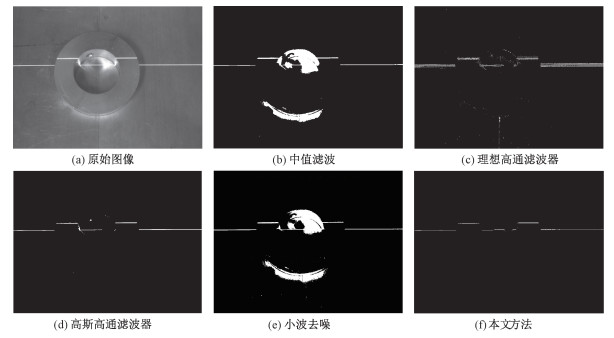
灰度相机采集到的原始图像(图 3(a))为值为0~255的二维矩阵, 先对图像做二值化处理, 其中激光照射区域光线亮度较大, 对应的像素值大。激光未照射的地方光线亮度小, 得到的图像较暗。将大于阈值的像素置为1, 否则为0。此时若待测物体表面存在镜面反光现象, 激光线容易在二值化图像中出现大块光斑, 影响激光实际位置的提取。在二值图像中检测连通域, 剔除较大的斑块, 最后使用图像均值滤波去除细小噪声, 得到降噪的最终图 3(f)。图 3给出我们算法与经典去噪算法(中值滤波、理想高通滤波器、高斯高通滤波器等)的比较结果。由结果可以看出, 对于存在镜面反射的情况, 我们的方法得到的图片更为清晰, 激光线的宽度最小, 精度最高。同时避免了原始图像中的光斑, 不被激光线的反射光线影响, 可以精确地提取出激光线在图像中的坐标。
|
Download:
|
| 图 3 不同算法去噪效果对比 Fig. 3 Denoising effects of different algorithms | |
表 1给出了运行时间的比较结果, 对同一幅图像, 我们的算法与中值滤波算法远快于其他算法。但中值滤波无法避免镜面反射的错误光线, 因此无法应用在实际使用中。由此可看出, 我们算法的去噪效果和计算效率的综合性能最优。
|
|
表 1 算法时间对比 Table 1 Comparison of algorithm time |
由激光三角法可知, 可将激光在图像中的偏移转化为物体的实际高度信息, 为获得精确的像素偏移, 需进行激光中线提取; 对于降噪得到图像Inew, 定义激光线的像素坐标为: 对第i列像素, 对降噪到的像素列做加权平均, 权值为图像Inew的灰度值。由此可得到激光线的像素坐标为
| $ \left(i, \frac{1}{H} \sum\limits_{j=1}^H I_{\text {new }}^{i, j} \times j\right), i=1, \cdots, W. $ | (3) |
对不同的激光中线提取算法进行测试, 当降噪后的图像中不存在或存在很少的噪声, 各种激光中心线提取算法都可以得到很好的结果。表 2对比了运行时间, 结果表明灰度重心法速度与在稳定度上达到了很好的均衡。可以在很短的时间内稳定地提取出激光中心线的坐标。
|
|
表 2 提取中线时间对比 Table 2 Time of extracting midline |
当原始图像中存在光斑时, 镜面反射会污染激光线的实际位置。如果直接剔除掉光斑, 则此处的激光线信息也会随之丢失。为了尽量恢复出物体的高度信息, 使用三次样条拟合根据周围的激光线信息恢复丢失的激光线。对已经恢复的激光线图像坐标, 记为(xi, yi), 其中xi∈[1, W]。我们希望可以找到样条f(x), 使得样条贴近所有已知点。即
| $ \min |f(x)-y| . $ | (4) |
这里直接用点的横坐标作为参数, 则样条的求解变为二次优化问题, 可以通过计算线性方程找到样条f(x)的最优解。求得样条f(x)后, 在样条曲线上采样, 选取新的样条曲线点(i, f(i)), i=1,…,W作为激光线的像素坐标。
2.3 扫描后的后处理经过函数标定、图像去噪等操作之后, 得到离散的点云数据反映了物体的实际高度, 但是由于数据是离散形式, 且不可避免地存在噪声, 难以直接应用在常见的测量、加工任务中。因此, 需要对采集的点云数据先进行去噪, 然后再进行三角网格重建, 最后的测量结果均是在三角网格模型上得到的。由于在实验中, 发现点云噪声不大, 因此, 只使用了滑动最小二乘法[20]进行滤波处理。为了获得比较好的网格模型, 使用IGR[14]进行网格重建, 接着使用MeshTGV[21]对得到的网格进行去噪, 最后使用Geodesics in Heat[22]计算测地线距离, 效果如图 4所示。

|
Download:
|
| 图 4 结果展示 Fig. 4 Results | |
用于对照比较的商业扫描仪是清波LM2108,其售价23 000元左右, 本文自建扫描仪硬件成本约2 300元。根据商业扫描仪使用说明上给出的参数, 其视野范围在28~34 mm, 而自建扫描仪的视野范围在45~55 mm。
3.2 纹理材料对比实验对比了木质的一些典型几何体, 包括: 立方体、半球、三棱柱、六棱柱, 图 5分别给出相应的测量得到的点云与重建网格的比较结果。由于商业扫描仪不提供曲面重建功能, 因此, 只展示其采集的点云数据结果。

|
Download:
|
| 图 5 木制物体高度测量及表面重建比较 Fig. 5 Height measurement and surface reconstruction of wooden objects | |
对于木制待测物品, 因为材料表面较为粗糙, 激光照射在物体表面主要为漫反射, 相机采取到的图片较为清晰, 激光线位置明确。我们的方案与某商业软件的方案都可以得到准确的深度数据, 恢复出点云数据, 进而通过IGR重建出待测物体的三维模型。根据采集得到的点云, 计算出形状的高度信息, 与真实物体的高度相比较, 表 3给出重建精度对比。由比较可以看出, 我们的方案在精度上较弱于某商业软件的方案, 但重建精度也达到了0.1 mm的量级。由于自建仪器采用直射式激光三角法搭建扫描仪, 选取了较大的相机镜头焦距, 单次拍照可以取得更大的相机视野, 恢复出的深度图更大。而商业软件为保证测量精度, 选取的镜头焦距较小, 造成工作视野较小, 无法将整个半球扫完全, 因此表 3中高度数据无法计算。
|
|
表 3 高度检测 Table 3 Heights detection |
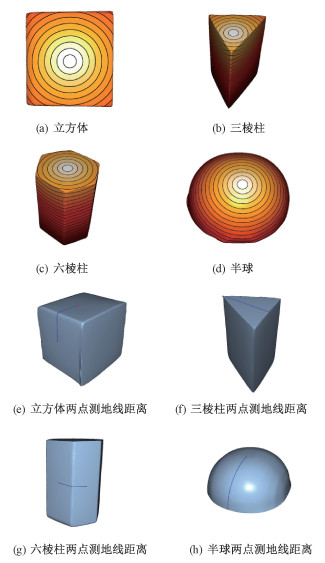
计算重建模型任意两点之间的测地线距离, 并与真实物体的测地线距离进行比较。图 6(a)~6(d)给出重建之后的测地线距离,图 6(e)~6(h)给出网格上任意两点的测地线路径, 表 4给出计算的测地线距离与实际距离的对比。实验结果表明我们搭建的平台在原始采集数据和几何重建、测量上都有稳定的精度。
|
Download:
|
| 图 6 测地线距离展示 Fig. 6 Geodesic distance | |
|
|
表 4 测地线距离对比 Table 4 Comparision of geodesic distances |
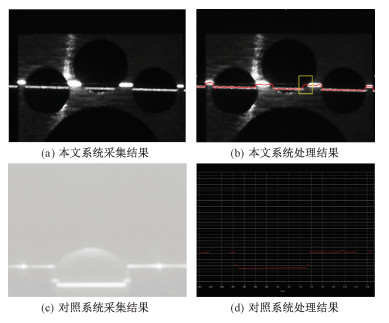
对比金属材质物体的扫描结果, 扫描同一金属物体的同一部分, 结果如图 7所示, 由于我们仪器的视野大于商业扫描仪, 因此, 可以扫描出完整的模型。虽然我们的方法也存在一些缺陷(图中黄色方框), 但是整体形状是完整的, 这些误差可以在后续重建过程中消除。
|
Download:
|
| 图 7 金属材质物体的采集图像和处理结果对比 Fig. 7 Images acquiring and processing of metal objects | |
分析图例可以发现, 商业软件在测量金属物体时无法正确地处理原始图片, 进而难以提取出激光线的准确位置。测量得到的深度数据存在大量缺失, 难以反映物体的实际表面情况。而我们的算法对金属物体针对金属反光的情况专门去噪处理, 使用样条拟合的方法恢复光污染的区域信息, 可以有效地测量出金属材质物体的深度信息。最后, 给出金属反光物体完整的扫描结果, 如图 8所示。

|
Download:
|
| 图 8 完整重建对比 Fig. 8 Comparison of reconstructions | |
本文搭建了基于直射式激光三角法的激光测距平台, 并针对金属材质物体表面镜面反射问题设计了激光线提取算法, 实现高精度的非接触式测量, 并且提供了一般测量仪不具有的几何重建与测地线距离测量功能。针对一般材质, 通过实验选择了合适的提取激光中线的方法与标定函数的方法, 并使用样条拟合激光条带, 提升了残缺激光数据上结果的准确性和测量点数量。通过对比激光测距仪在不同材质不同形状物体上的表现, 结果显示自建扫描仪在常规材质下取得了与商业系统相似的精度, 而在测量金属物体时能更好地处理反光情况, 得到更大的感受视野与测量点。我们的激光测量系统可以实现1 mm内的重建精度, 并拥有更大测量视野, 可以直接处理商业软件无法直接扫描的物体。
本文也存在一些不足之处, 主要在于经过图像处理后, 直接对得到的点云进行了重建, 点云处理的流程并不完整。虽然经过图像处理得到的点云信息噪声并不明显, 但是依旧可以加入点云去噪流程, 从而方便后续的几何重建过程; 其次, 扫描仪无法一次扫全整个物体, 要想得到一个完整的模型需要多次扫描, 并进行点云配准, 而在某些激光扫不到的地方容易产生空洞, 需要依据先验知识补全点云; 最后扫描仪可能产生数量过多的点云, 给后续的处理带来内存和效率的压力, 点云简化也是需要进行的操作之一。因此, 未来的工作主要集中于设计一个新的移动模块, 使其能够自动旋转模型, 从而得到完整的模型, 进而实现从物体到重建模型的全自动化流程,并且对点云处理流程进行完善。
| [1] |
Hosni Y, Ferreira L. Laser based system for reverse engineering[J]. Computers & Industrial Engineering, 1994, 26(2): 387-394. Doi:10.1016/0360-8352(94)90072-8 |
| [2] |
França J G D M, Gazziro M A, Ide A N, et al. A 3d scanning system based on laser triangulation and variable field of view[C]//2005 IEEE International Conference on Image Processing. September 14, 2005, Genova, Italy. IEEE, 2005: I-425. DOI: 10.1109/ICIP.2005.1529778.
|
| [3] |
Brosed F J, Aguilar J J, Guillomía D, et al. 3D geometrical inspection of complex geometry parts using a novel laser triangulation sensor and a robot[J]. Sensors, 2011, 11(1): 90-110. Doi:10.3390/s110100090 |
| [4] |
Alempijevic A, Dissanayake G. An efficient algorithm for line extraction from laser scans[C]//2004 IEEE Conference on Robotics, Automation and Mechatronics. December 01-03, 2004, Singapore. IEEE, 2004: 970-974. DOI: 10.1109/RAMECH.2004.1438050.
|
| [5] |
Forest J, Salvi J, Cabruja E, et al. Laser stripe peak detector for 3D scanners: a FIR filter approach[C]//Proceedings of the 17th International Conference on Pattern Recognition. August 26, 2004. Cambridge, UK. IEEE, 2004: 646-649. DOI: 10.1109/ICPR.2004.1334612.
|
| [6] |
Bernardini F, Mittleman J, Rushmeier H, et al. The ball-pivoting algorithm for surface reconstruction[J]. IEEE Transactions on Visualization and Computer Graphics, 1999, 5(4): 349-359. Doi:10.1109/2945.817351 |
| [7] |
Amenta N, Choi S, Kolluri R K. The power crust[C]//Proceedings of the sixth ACM symposium on Solid modeling and applications. May, 2001, New York, NY, USA. ACM, 2001: 249-266. DOI: 10.1145/376957.376986.
|
| [8] |
Kazhdan M, Hoppe H. Screened Poisson surface reconstruction[J]. ACM Transactions on Graphics, 2013, 32(3): 1-13. Doi:10.1145/2487228.2487237 |
| [9] |
Ohtake Y, Belyaev A, Alexa M, et al. Multi-level partition of unity implicits[C]//ACM SIGGRAPH 2005 Courses. July, 2005, New York, NY, USA. ACM, 2005: 173-es. DOI: 10.1145/1198555.1198649.
|
| [10] |
Carr J C, Beatson R K, Cherrie J B, et al. Reconstruction and representation of 3D objects with radial basis functions[C]//Proceedings of the 28th annual conference on Computer graphics and interactive techniques. August 2001, New York, NY, USA. ACM, 2001: 67-76. DOI: 10.1145/383259.383266.
|
| [11] |
Groueix T, Fisher M, Kim V G, et al. A Papier-Mache approach to learning 3D surface generation[C]//2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. June 2018, Salt Lake City, UT, USA. IEEE, 2018: 216-224. DOI: 10.1109/CVPR.2018.00030.
|
| [12] |
Park J J, Florence P, Straub J, et al. DeepSDF: learning continuous signed distance functions for shape representation[C]//2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). June 2019, Long Beach, CA, USA. IEEE, 2019: 165-174. DOI: 10.1109/CVPR.2019.00025.
|
| [13] |
Lorensen W E, Cline H E. Marching cubes: a high resolution 3D surface construction algorithm[J]. ACM SIGGRAPH Computer Graphics, 1987, 21(4): 163-169. Doi:10.1145/37402.37422 |
| [14] |
Gropp A, Yariv L, Haim N, et al. Implicit geometric regularization for learning shapes[C]//Proceedings of the 37th International Conference on Machine Learning. July 2020, JMLR. org. ACM, 2020: 3789-3799. DOI: 10.5555/3524938.3525293.
|
| [15] |
Zhou K, Synder J, Guo B N, et al. Iso-charts: stretch-driven mesh parameterization using spectral analysis[C]//Proceedings of the 2004 Eurographics/ACM SIGGRAPH symposium on Geometry processing. July 2004, New York, NY, USA. ACM, 2004: 45-54. DOI: 10.1145/1057432.1057439.
|
| [16] |
Wang W G, Shen J B, Yang R G, et al. Saliency-aware video object segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 40(1): 20-33. Doi:10.1109/TPAMI.2017.2662005 |
| [17] |
Zelinka S, Garland M. Similarity-based surface modelling using geodesic fans[C]//SIGGRAPH & apos; 04: ACM SIGGRAPH 2004 Sketches. New York: ACM, 2004. DOI: 10.1145/1186223.1186344.
|
| [18] |
Zou Q, Zhang J Y, Deng B L, et al. Iso-level tool path planning for free-form surfaces[J]. Computer-Aided Design, 2014, 53: 117-125. Doi:10.1016/j.cad.2014.04.006 |
| [19] |
Peyré G, Cohen L D. Geodesic methods for shape and surface processing[M]//Advances in Computational Vision and Medical Image Processing. Dordrecht: Springer Netherlands, 2008: 29-56. DOI: 10.1007/978-1-4020-9086-8_2.
|
| [20] |
Alexa M, Behr J, Cohen-Or D, et al. Computing and rendering point set surfaces[J]. IEEE Transactions on Visualization and Computer Graphics, 2003, 9(1): 3-15. Doi:10.1109/TVCG.2003.1175093 |
| [21] |
Liu Z, Li Y L, Wang W N, et al. Mesh total generalized variation for denoising[J]. IEEE Transactions on Visualization and Computer Graphics, 2022, 28(12): 4418-4433. Doi:10.1109/TVCG.2021.3088118 |
| [22] |
Crane K, Weischedel C, Wardetzky M. The heat method for distance computation[J]. Communications of the ACM, 2017, 60(11): 90-99. Doi:10.1145/3131280 |
 2023, Vol. 40
2023, Vol. 40 


