2. 安徽新华学院商学院,合肥 230088
2. School of Business, Xinhua University of Anhui, Hefei 230088, China
若X代表投资,T代表投资周期,δ表示折扣率,则Xe-δT表示投资X在T时刻贴现到当前时刻的现值收益。有的文献也称Xe-δT为利率贴现模型。通过现值贴现,可以将不同时点的收益或者损失折现到当前时刻点,从而有益于研究和比较。关于贴现模型的研究有许多,Goovaerts等[1]针对线性形式的随机变量,给出贴现模型分布函数上界的近似值。Hu和Cheung[2]、Zhuang等[3]利用贴现模型,获得了特定条件下针对不同风险投保的保单限额和免赔额的最优分配权重。类似的研究还有很多,如文献[4-8]。
随机占优理论由Hardar和Russell[9]、Hanoch和Levy[10]、Rothschild和Stiglitz[11]研究不确定性决策问题而提出。Hardar和Russell[9]、Hanoch和Levy[10]分别建立了一阶随机占优和二阶随机占优理论。Hammond[12]、Meyer[13]研究了风险偏好型随机占优理论。随机占优理论可用于投资组合的比较,Hardar和Russell[14]、Tesfatsion[15]在二元情形下指出, 若投资收益满足独立同分布条件,对于风险厌恶者而言,非负等权重的投资组合是最优选择,而仅仅投资于单一的项目是最差的选择。Li和Wong[16]将前者工作延伸至多元情形。Guo和Wong[17]基于特定形式的效用函数形式得到了一些关于风险厌恶型和风险偏好型的多元随机占优结果。
本文将贴现模型与随机占优理论进行结合,考虑时间因素对随机占优结果的影响,并基于几种常见的随机占优情形探究不同风险偏好投资者的决策行为。
1 定义与等价条件 1.1 随机占优在介绍随机变量间的随机占优序定义之前,先对其支撑集做出如下假设。
假设1.1 设随机变量X和Y的分布函数分别为F和G,共同支撑为[a, b],其中-∞ < a≤b < ∞,当x≤a时,F(x)=G(x)=0;当x≥b时F(x)=G(x)=1。
定义1.1 [18] 在假设1.1下,
a.若对任意x∈[a, b], F(x)≤G(x),且至少存在一个x0∈[a, b]使得不等式严格成立,则称X一阶随机占优于Y,记作X≥FSDY。
b. 若对任意
c. 若对任意
易见,
引理1.1 [18] a.X≥FSDY等价于,对任意函数U∈ U1, E[U(X)]≥E[U(Y)],且至少存在一个U0∈ U1使得不等式严格成立,其中 U1 ={U: U′≥0}。
b.X≥SSDY等价于,对任意函数U∈ U2, E[U(X)]≥E[U(Y)],且至少存在一个U0∈ U2使得不等式严格成立,其中U2 ={U: U′≥0, U″≤0}。
c.X≥RSSDY等价于,对任意函数U∈ U3, E[U(X)]≥E[U(Y)],且至少存在一个U0∈ U3使得不等式严格成立,其中U3 ={U: U′≥0, U″≥0}。
1.2 超优记
则称βn超优于αn,记作βn≥Mαn。
下面的引理1.2揭示,被超优向量可以由超优向量经过有限次的T矩阵变换得到。
引理1.2 [19] 若βn≥Mαn,则αn可由βn经过至多n-1次T矩阵变换得到,T矩阵形式为T=λI+(1-λ)Q, 1/2≤λ≤1。其中I为单位矩阵,Q为交换两列元素的置换矩阵。
2 单笔投资的利率贴现模型比较本节将建立Xe-δT依不同占优序随机递减的充分条件。
定理2.1 设X1、X2和T1、T2为2列非负随机变量,Xi与Ti独立,i=1, 2。对任意的δ2≥δ1>0,若X1≥FSDX2, T1≤FSDT2, 则有X1e-δ1T1≥FSDX2e-δ2T2。
证明 由T1≤FSDT2以及定义1.1可得δ1T1≤FSDδ1T2。由于δ2≥δ1,易证δ1T2≤FSDδ2T2。因此有δ1T1≤FSDδ1T2≤FSDδ2T2。再注意到e-x是递减函数,于是
| $ \mathrm{e}^{-\delta_{1} T_{1}} \geqslant_{\mathrm{FSD}} \mathrm{e}^{-\delta_{1} T_{2}} \geqslant_{\mathrm{FSD}} \mathrm{e}^{-\delta_{2} T_{2}}. $ |
于是,对任意的递增函数U(x)∈ U1,
| $ \begin{align*} \mathrm{E}\left[U\left(X_{1} \mathrm{e}^{-\delta_{1} T_{1}}\right)\right] & =\mathrm{E}\left[\mathrm{E}\left(U\left(X_{1} \mathrm{e}^{-\delta_{1} T_{1}}\right) \mid X_{1}\right)\right] \\ & \geqslant \mathrm{E}\left[\mathrm{E}\left(U\left(X_{1} \mathrm{e}^{-\delta_{2} T_{2}}\right) \mid X_{1}\right)\right] \\ & =\mathrm{E}\left[U\left(X_{1} \mathrm{e}^{-\delta_{2} T_{2}}\right)\right] . \end{align*} $ | (1) |
又因为X1≥FSDX2,可以推出
| $ \begin{align*} \mathrm{E}\left[U\left(X_{1} \mathrm{e}^{-\delta_{2} T_{2}}\right)\right] & =\mathrm{E}\left[\mathrm{E}\left(U\left(X_{1} \mathrm{e}^{-\delta_{2} T_{2}}\right) \mid T_{2}\right)\right] \\ & \geqslant \mathrm{E}\left[\mathrm{E}\left(U\left(X_{2} \mathrm{e}^{-\delta_{2} T_{2}}\right) \mid T_{2}\right)\right] \\ & =\mathrm{E}\left[U\left(X_{2} \mathrm{e}^{-\delta_{2} T_{2}}\right)\right] . \end{align*} $ | (2) |
结合式(1)和式(2)可得E[U(X1e-δ1T1)]≥E[U(X2e-δ2T2)]。故有X1e-δ1T1≥FSDX2e-δ2T2。
定理2.1表明,在一阶随机占优情形下,若后者折现率大于前者,投资者更愿意选择收益更高、周期更短的投资。
定理2.2 设X1、X2和T1、T2为2列非负随机变量, Xi与Ti独立,i=1, 2。对任意的δ2≥δ1> 0, 若X1≥SSDX2, T1≤FSDT2, 则X1e-δ1T1≥SSDX2e-δ2T2。
证明 因T1≤FSDT2,由定义1.1和δ2≥δ1>0可得,对任意的t≥0,
| $ \begin{aligned} \mathrm{P}\left(\delta_{1} T_{1} \leqslant t\right) & =\mathrm{P}\left(T_{1} \leqslant \frac{t}{\delta_{1}}\right) \geqslant \mathrm{P}\left(T_{2} \leqslant \frac{t}{\delta_{1}}\right) \\ & \geqslant \mathrm{P}\left(T_{2} \leqslant \frac{t}{\delta_{2}}\right)=\mathrm{P}\left(\delta_{2} T_{2} \leqslant t\right), \end{aligned} $ |
这表明δ1T1≤FSDδ2T2。注意到e-x是递减函数,于是e-δ1T1≥FSDe-δ2T2,进而可得e-δ1T1≥SSDe-δ2T2。因此,对任意的增凹函数U(x)∈ U2,
| $ \begin{align*} \mathrm{E}\left[U\left(X_{1} \mathrm{e}^{-\delta_{2} T_{2}}\right)\right] & =\mathrm{E}\left[\mathrm{E}\left(U\left(X_{1} \mathrm{e}^{-\delta_{2} T_{2}}\right) \mid X_{1}\right)\right] \\ & \leqslant \mathrm{E}\left[\mathrm{E}\left(U\left(X_{1} \mathrm{e}^{-\delta_{1} T_{1}}\right) \mid X_{1}\right)\right] \\ & =\mathrm{E}\left[U\left(X_{1} \mathrm{e}^{-\delta_{1} T_{1}}\right)\right] . \end{align*} $ | (3) |
再由X1≥SSDX2得
| $ \begin{align*} \mathrm{E}\left[U\left(X_{2} \mathrm{e}^{-\delta_{2} T_{2}}\right)\right] & =\mathrm{E}\left[\mathrm{E}\left(U\left(X_{2} \mathrm{e}^{-\delta_{2} T_{2}}\right) \mid T_{2}\right)\right] \\ & \leqslant \mathrm{E}\left[\mathrm{E}\left(U\left(X_{1} \mathrm{e}^{-\delta_{2} T_{2}}\right) \mid T_{2}\right)\right] \\ & =\mathrm{E}\left[U\left(X_{1} \mathrm{e}^{-\delta_{2} T_{2}}\right)\right] . \end{align*} $ | (4) |
结合式(3)和式(4),对任意的U(x)∈ U2,有
| $ \mathrm{E}\left[U\left(X_{1} \mathrm{e}^{-\delta_{1} T_{1}}\right)\right] \geqslant \mathrm{E}\left[U\left(X_{2} \mathrm{e}^{-\delta_{2} T_{2}}\right)\right], $ |
即有
定理2.2揭示,在二阶随机占优意义下,投资者更偏好周期短且风险小的投资。
定理2.3 设X1、X2和T1、T2为2列非负随机变量, Xi与Ti独立,i=1, 2。对任意的δ2≥δ1> 0, 若以下条件之一成立,则有X1e-δ1T1≥RSSDX2e-δ2T2。
(a) X1≥RSSDX2, T1≤SSDT2; (b) X1≥RSSDX2, T1≤FSDT2; (c) X1≥FSDX2, T1≤SSDT2.
证明 仅给出条件(a)的证明,条件(b)和(c)的证明类似,故略去。若T1>0时,则对任意的x>0,
| $ \begin{gathered} \frac{\int_{-\infty}^{x} \mathrm{P}\left(\delta_{1} T_{1} \leqslant u\right) \mathrm{d} u \quad \delta_{1} \int_{-\infty}^{x \delta_{1}} \mathrm{P}\left(T_{1} \leqslant u\right) \mathrm{d} u}{\int_{-\infty}^{x} \mathrm{P}\left(\delta_{2} T_{1} \leqslant u\right) \mathrm{d} u \quad \delta_{2} \int_{-\infty}^{x / \delta_{2}} \mathrm{P}\left(T_{1} \leqslant u\right) \mathrm{d} u}= \\ \frac{\delta_{1} \int_{0}^{x \delta_{1}} \mathrm{P}\left(T_{1} \leqslant u\right) \mathrm{d} u}{\delta_{2} \int_{0}^{x \sqrt{\delta_{2}}} \mathrm{P}\left(T_{1} \leqslant u\right) \mathrm{d} u} . \end{gathered} $ |
注意到δ2≥δ1>0,进一步可以得
| $ \begin{aligned} & \frac{\int_{-\infty}^{x} \mathrm{P}\left(\delta_{1} T_{1} \leqslant u\right) \mathrm{d} u}{\int_{-\infty}^{x} \mathrm{P}\left(\delta_{2} T_{1} \leqslant u\right) \mathrm{d} u}=\frac{\int_{0}^{x} \mathrm{P}\left(\delta_{1} T_{1} \leqslant u\right) \mathrm{d} u}{\int_{0}^{x} \mathrm{P}\left(\delta_{2} T_{1} \leqslant u\right) \mathrm{d} u} \\ & =\frac{\delta_{1}}{\delta_{2}}\left[1+\frac{\int_{x / \delta_{2}}^{x / \delta_{1}} \mathrm{P}\left(T_{1} \leqslant u\right) \mathrm{d} u}{\int_{0}^{x / \delta_{2}} \mathrm{P}\left(T_{1} \leqslant u\right) \mathrm{d} u}\right] \\ & \geqslant \frac{\delta_{1}}{\delta_{2}}\left[1+\frac{\int_{x / \delta_{2}}^{x / \delta_{1}} \mathrm{P}\left(T_{1} \leqslant x / \delta_{2}\right) \mathrm{d} u}{\int_{0}^{x \delta_{2}} \mathrm{P}\left(T_{1} \leqslant x / \delta_{2}\right) \mathrm{d} u}\right] \\ & =\frac{\delta_{1}}{\delta_{2}}\left[1+\frac{\left.\mathrm{P}\left(T_{1} \leqslant x / \delta_{2}\right) \frac{\delta_{2}-\delta_{1}}{\delta_{2} \delta_{1}} x\right]}{\mathrm{P}\left(T_{1} \leqslant x / \delta_{2}\right) \frac{1}{\delta_{2}} x}\right] \\ & =\frac{\delta_{1}}{\delta_{2}}\left[1+\frac{\delta_{2}-\delta_{1}}{\delta_{1}}\right]=1 . \end{aligned} $ |
因此,对任意的x>0,都有
| $ \int_{-\infty}^{x} \mathrm{P}\left(\delta_{1} T_{1} \leqslant u\right) \mathrm{d} u \geqslant \int_{-\infty}^{x} \mathrm{P}\left(\delta_{2} T_{1} \leqslant u\right) \mathrm{d} u, $ |
即δ1T1≤SSDδ2T1,进而由文献[20]中的定理4.A.1得-δ1T1≥RSSD-δ2T1。同理,由条件T1≤SSDT2可知-δ2T1≥RSSD-δ2T2。因此-δ1T1≥RSSD-δ2T2。进而得e-δ1T1≥RSSDe-δ2T2,则对任意的增凸函数U(x)∈ U3,
| $ \begin{align*} \mathrm{E}\left[U\left(X_{2} \mathrm{e}^{-\delta_{1} T_{1}}\right)\right] & =\mathrm{E}\left[\mathrm{E}\left(U\left(X_{2} \mathrm{e}^{-\delta_{1} T_{1}}\right) \mid X_{2}\right)\right] \\ & \geqslant \mathrm{E}\left[\mathrm{E}\left(U\left(X_{2} \mathrm{e}^{-\delta_{2} T_{2}}\right) \mid X_{2}\right)\right] \\ & =\mathrm{E}\left[U\left(X_{2} \mathrm{e}^{-\delta_{2} T_{2}}\right)\right] . \end{align*} $ | (5) |
类似地,由条件X1≥RSSDX2得
| $ \begin{align*} \mathrm{E}\left[U\left(X_{1} \mathrm{e}^{-\delta_{1} T_{1}}\right)\right] & =\mathrm{E}\left[\mathrm{E}\left(U\left(X_{1} \mathrm{e}^{-\delta_{1} T_{1}}\right) \mid T_{1}\right)\right] \\ & \geqslant \mathrm{E}\left[\mathrm{E}\left(U\left(X_{2} \mathrm{e}^{-\delta_{1} T_{1}}\right) \mid T_{1}\right)\right] \\ & =\mathrm{E}\left[U\left(X_{2} \mathrm{e}^{-\delta_{1} T_{1}}\right)\right] . \end{align*} $ | (6) |
因此,对任意增凸函数U(x)∈ U3,成立
| $ \mathrm{E}\left[U\left(X_{1} \mathrm{e}^{-\delta_{1} T_{1}}\right)\right] \geqslant \mathrm{E}\left[U\left(X_{2} \mathrm{e}^{-\delta_{2} T_{2}}\right)\right] . $ |
若T1=0时,由
由于非负独立随机变量的随机占优关系关于卷积封闭[20],于是有如下推论。
推论2.1 设{X1, …, Xn}和{Y1, …, Yn}为2列非负独立随机变量,{T1, …, Tn}和{S1, …, Sn}为另外2列非负独立随机变量,且{X1, …, Xn}与{T1, …, Tn}独立,{Y1, …, Yn}与{S1, …, Sn}独立,
a. 若
b.若Xi≥SSDYi, Ti≤FSDSi,且δ′i≥δi>0, i=1, …, n, 则有
c. 若
将Xi视为第i笔投资,Ti为第i笔投资的回报时间,δi为其贴现率,则
| $ \frac{1}{2} X_{1}+\frac{1}{2} X_{2} \geqslant_{\mathrm{SSD}} \alpha_{1} X_{1}+\alpha_{2} X_{2} \geqslant_{\mathrm{SSD}} X_{i}, \quad i=1, 2 . $ |
考虑一系列投资的非负凸组合
| $ S_{n}=\left\{\left(s_{1}, \cdots, s_{n}\right)^{\mathrm{T}}: 0 \leqslant s_{i} \leqslant 1, \sum\limits_{i=1}^{n} s_{i}=1\right\} . $ |
Li和Wong[16]得到如下引理3.1。
引理3.1 [16] 若{X1, …, Xn}为一列独立同分布随机变量,若
| $ \frac{1}{n} \sum\limits_{i=1}^{n} X_{i} \geqslant_{\mathrm{SSD}} \sum\limits_{i=1}^{n} \alpha_{i} X_{i} \geqslant_{\mathrm{SSD}} X_{i}, i=1, 2, \cdots, n. $ |
对于不同权重的投资组合,Egozcue和Wong[21]借助超优序得到如下引理3.2。
引理3.2 [21] 设{X1, …, Xn}为一列独立同分布随机变量,
风险偏好型随机占优序也有类似的结果。
引理3.3 [17] 设{X1, …, Xn}为一列独立同分布随机变量,
将引理3.2和引理3.3中的Xi视为
定理3.1 设{X1, …, Xn}与{T1, …, Tn}为2列独立同分布的随机变量,且Xi与Ti独立,i=1, …, n。向量αn∈Sn以及βn∈Sn。若αn≥Mβn, 则
| $ \begin{aligned} & \sum\limits_{i=1}^{n} \beta_{i} X_{i} \mathrm{e}^{-\delta T_{i}} \geqslant_{\text {SSD }} \sum\limits_{i=1}^{n} \alpha_{i} X_{i} \mathrm{e}^{-\delta T_{i}} \\ & \sum\limits_{i=1}^{n} \alpha_{i} X_{i} \mathrm{e}^{-\delta T_{i}} \geqslant_{\text {RSSD}} \sum\limits_{i=1}^{n} \beta_{i} X_{i} \mathrm{e}^{-\delta T_{i}} . \end{aligned} $ |
对任意向量αn∈Sn,由于始终成立
| $ (1, 0, \cdots, 0)^{\mathrm{T}} \geqslant_{\mathrm{M}} \boldsymbol{\alpha}_{n} \geqslant_{\mathrm{M}}(1 / n, 1 / n, \cdots, 1 / n)^{\mathrm{T}} \text {, } $ |
利用定理3.1可得到如下结论。
定理3.2 设{X1, …, Xn}与{T1, …, Tn}为2列独立同分布随机变量,且Xi与Ti独立,i=1, …, n。若向量αn∈Sn, 则
| $ \begin{aligned} & \frac{1}{n} \sum\limits_{i=1}^{n} X_{i} \mathrm{e}^{-\delta T_{i}} \geqslant_{\mathrm{SSD}} \sum\limits_{i=1}^{n} \alpha_{i} X_{i} \mathrm{e}^{-\delta T_{i}} \geqslant_{\mathrm{SSD}} X_{i}, \\ & X_{i} \geqslant_{\text {RSSD}} \sum\limits_{i=1}^{n} \alpha_{i} X_{i} \mathrm{e}^{-\delta T_{i}} \geqslant_{\text {RSSD}} \frac{1}{n} \sum\limits_{i=1}^{n} X_{i} \mathrm{e}^{-\delta T_{i}}. \end{aligned} $ |
引理3.2和引理3.3中独立同分布的条件非常苛刻,该条件是否可以舍去?下面的例3.1给出了答案。
例3.1 设X1和X2独立,X1~N(0.5, 0.32),且X2~N(0.3, 0.42)。向量α2, β2 ∈ S2满足α2≥Mβ2, 则
| $ \begin{aligned} & \alpha_{1} X_{1}+\alpha_{2} X_{2} \sim N\left(0.2 \alpha_{1}+0.3\right. ,\\ & \left.0.16\left(1-\alpha_{1}\right)^{2}+0.09 \alpha_{1}^{2}\right), \\ & \beta_{1} X_{1}+\beta_{2} X_{2} \sim N\left(0.2 \beta_{1}+0.3\right., \\ & \left.0.16\left(1-\beta_{1}\right)^{2}+0.09 \beta_{1}^{2}\right). \end{aligned} $ |
要使α1X1+α2X2≥SSDβ1X1+β2X2,需
| $ \left\{\begin{array}{l} 0.2 \alpha_1+0.3 \geqslant 0.2 \beta_1+0.3, \\ 0.16\left(1-\alpha_1\right)^2+0.09 \alpha_1^2 \leqslant 0.16\left(1-\beta_1\right)^2+0.09 \beta_1^2 . \end{array}\right. $ |
即要求α1≥β1,且α1+β1≤32/25。若取向量α2 =(19/25, 6/25), β2 =(16/25, 9/25), 则不能满足上述要求。所以,引理3.2和引理3.3中独立同分布的条件是不可删去的。
在特殊情形下,可删去引理3.2中独立同分布的条件。为此,引入排列增(减)的概念。
定义3.1 [2] 对于函数g(x1, …, xn), 若对任意的1≤i < j≤n满足
| $ \begin{aligned} & \left(x_{i}-x_{j}\right)\left(g\left(x_{1}, \cdots, x_{i}, \cdots, x_{j}, \cdots, x_{n}\right)-\right. \\ & \left.g\left(x_{1}, \cdots, x_{j}, \cdots, x_{i}, \cdots, x_{n}\right)\right) \leqslant(\geqslant) 0, \end{aligned} $ |
则称g(x1, …, xn)为排列增(减)函数。
对于SSD序,我们可证如下引理3.4。
引理3.4 假定随机向量(X1, …,Xn)的联合概率密度函数f(x1, …,xn)为排列增的,若
证明 先证n=2的情形。若向量 α2, β2 ∈ S2,且α2≥Mβ2,则由超优序的定义得
| $ \begin{gathered} \alpha_{1} \geqslant \alpha_{2}, \beta_{1} \geqslant \beta_{2}, \alpha_{1} \geqslant \beta_{1} ,\\ \alpha_{1}+\alpha_{2}=\beta_{1}+\beta_{2}=1. \end{gathered} $ |
当x2>x1时,由α1≥β1得
| $ \begin{aligned} & \left(\alpha_{1} x_{2}+\alpha_{2} x_{1}\right)-\left(\beta_{1} x_{2}+\beta_{2} x_{1}\right) \\ & =\left(\alpha_{1}-\beta_{1}\right) x_{2}+\left(\alpha_{2}-\beta_{2}\right) x_{1} \\ & =\left(\alpha_{1}-\beta_{1}\right) x_{2}+\left[1-\alpha_{1}-\left(1-\beta_{1}\right)\right] x_{1} \\ & =\left(\alpha_{1}-\beta_{1}\right)\left(x_{2}-x_{1}\right) \geqslant 0, \end{aligned} $ |
即有α1x2+α2x1≥β1x2+β2x1。同理,由α1≥α2, β1≥β2得
| $ \begin{aligned} & \alpha_{1} x_{2}+\alpha_{2} x_{1} \geqslant \alpha_{1} x_{1}+\alpha_{2} x_{2}, \beta_{1} x_{2}+\beta_{2} x_{1} \geqslant \\ &~~~~~~~ \beta_{2} x_{2}+\beta_{1} x_{1}. \end{aligned} $ |
又由
| $ \begin{gathered} x_{1}+x_{2}=\left(\alpha_{2} x_{2}+\alpha_{1} x_{1}\right)+\left(\alpha_{1} x_{2}+\alpha_{2} x_{1}\right)= \\ \left(\beta_{1} x_{2}+\beta_{2} x_{1}\right)+\left(\beta_{2} x_{2}+\beta_{1} x_{1}\right), \end{gathered} $ |
可以推知
| $ \begin{gathered} \alpha_{1} x_{2}+\alpha_{2} x_{1} \geqslant \beta_{1} x_{2}+\beta_{2} x_{1} \geqslant \beta_{2} x_{2}+ \\ \beta_{1} x_{1} \geqslant \alpha_{2} x_{2}+\alpha_{1} x_{1}. \end{gathered} $ |
因此对任意的函数U(x)∈ U2,
| $ \begin{aligned} & U\left(\beta_{1} x_{2}+\beta_{2} x_{1}\right)-U\left(\alpha_{1} x_{2}+\alpha_{2} x_{1}\right) \leqslant 0 \\ & U\left(\alpha_{1} x_{1}+\alpha_{2} x_{2}\right)+U\left(\alpha_{1} x_{2}+\alpha_{2} x_{1}\right) \\ & \leqslant U\left(\beta_{1} x_{1}+\beta_{2} x_{2}\right)+U\left(\beta_{1} x_{2}+\beta_{2} x_{1}\right). \end{aligned} $ |
进一步可得
| $ \mathrm{E}\left[U\left(\beta_{1} X_{1}+\beta_{2} X_{2}\right)\right]-\mathrm{E}\left[U\left(\alpha_{1} X_{1}+\alpha_{2} X_{2}\right)\right]\\ =\iint\left[U\left(\beta_{1} x_{1}+\beta_{2} x_{2}\right)-U\left(\alpha_{1} x_{1}+\alpha_{2} x_{2}\right)\right] f\left(x_{1}, x_{2}\right) \mathrm{d} x_{1} \mathrm{~d} x_{2}\\ =\iint\limits_{x_{2}>x_{1}}\left[U\left(\beta_{1} x_{1}+\beta_{2} x_{2}\right)-U\left(\alpha_{1} x_{1}+\alpha_{2} x_{2}\right)\right] f\left(x_{1}, x_{2}\right) \mathrm{d} x_{1} \mathrm{~d} x_{2}+\\ \iint\limits_{x_{1} \geq x_{2}}\left[U\left(\beta_{1} x_{1}+\beta_{2} x_{2}\right)-U\left(\alpha_{1} x_{1}+\alpha_{2} x_{2}\right)\right] f\left(x_{1}, x_{2}\right) \mathrm{d} x_{1} \mathrm{~d} x_{2}\\ =\iint\limits_{x_{2}>x_{1}}\left[U\left(\beta_{1} x_{1}+\beta_{2} x_{2}\right)-U\left(\alpha_{1} x_{1}+\alpha_{2} x_{2}\right)\right] f\left(x_{1}, x_{2}\right) \mathrm{d} x_{1} \mathrm{~d} x_{2}+\\ \iint\limits_{x_{2}>x_{1}}\left[U\left(\beta_{1} x_{2}+\beta_{2} x_{1}\right)-U\left(\alpha_{1} x_{2}+\alpha_{2} x_{1}\right)\right] f\left(x_{2}, x_{1}\right) \mathrm{d} x_{1} \mathrm{~d} x_{2} $ |
| $ \begin{aligned} \geqslant & \iint\limits_{x_{2}>x_{1}}\left[U\left(\beta_{1} x_{1}+\beta_{2} x_{2}\right)-U\left(\alpha_{1} x_{1}+\alpha_{2} x_{2}\right)\right] f\left(x_{1}, x_{2}\right) \mathrm{d} x_{1} \mathrm{~d} x_{2}+ \\ & \iint\limits_{x_{2}>x_{1}}\left[U\left(\beta_{1} x_{2}+\beta_{2} x_{1}\right)-U\left(\alpha_{1} x_{2}+\alpha_{2} x_{1}\right)\right] f\left(x_{1}, x_{2}\right) \mathrm{d} x_{1} \mathrm{~d} x_{2} \\ = & \iint\limits_{x_{2}>x_{1}}\left[U\left(\beta_{1} x_{1}+\beta_{2} x_{2}\right)+U\left(\beta_{2} x_{1}+\beta_{1} x_{2}\right)-U\left(\alpha_{1} x_{1}+\alpha_{2} x_{2}\right)-\right. \\ & \left.U\left(\alpha_{2} x_{1}+\alpha_{1} x_{2}\right)\right] f\left(x_{1}, x_{2}\right) \mathrm{d} x_{1} \mathrm{~d} x_{2} \geqslant 0 \end{aligned} $ |
上述推导过程中第3个等号成立的原因有二:一是因为将第2个积分中交换了变量的命名方式,积分值不变;二是因为x2=x1时,第2个积分的被积函数等于0。第1个不等号是因为U(β1x2+β2x1)-U(α1x2+α2x1)≤0,且f(x1, x2)为排列增函数,故当x2>x1时,成立f(x1, x2)>f(x2, x1)。因此由引理1.1可得β1X1+β2X2≥SSDα1X1+α2X2。
再考虑n≥3情形,由于αn≥Mβn,因此βn可由αn经过有限次T变换得到,即βn=TkTk-1… T1αn, k≤n-1。不失一般性,假定
| $ \begin{aligned} & \boldsymbol{T}_{1}=\lambda \boldsymbol{I}+(1-\lambda) \boldsymbol{Q}_{1}=\left(\begin{array}{lll} \lambda & & \\ & \ddots & \\ & & \lambda \end{array}\right)+ \\ & (1-\lambda)\left(\begin{array}{lllll} 0 & 1 & & & \\ 1 & 0 & & & \\ & & 1 & & \\ & & & \ddots & \\ & & & & 1 \end{array}\right)= \\ & \left(\begin{array}{ccccc} \lambda & 1-\lambda & & & \\ 1-\lambda & \lambda & & & \\ & & 1 & & \\ & & & \ddots & \\ & & & & 1 \end{array}\right), \end{aligned} $ |
其中1/2≤λ≤1。令
| $ \begin{aligned} & \sum\limits_{i=1}^{n} \gamma_{i} X_{i}=\left(\lambda \alpha_{1}+(1-\lambda) \alpha_{2}\right) X_{1}+ \\ & \left(\lambda \alpha_{2}+(1-\lambda) \alpha_{1}\right) X_{2}+\sum\limits_{i=3}^{n} \alpha_{i} X_{i}, \end{aligned} $ |
若
| $ \begin{aligned} \gamma_{n}= & \left(\lambda \alpha_{1}+(1-\lambda) \alpha_{2}, \lambda \alpha_{2}+\right. \\ & \left.(1-\lambda) \alpha_{1}, 0, \cdots, 0\right)^{\mathrm{T}}. \end{aligned} $ |
由于1/2≤λ≤1, α1≥α2且满足
| $ \left(\alpha_{1}, \alpha_{2}\right)^{\mathrm{T}} \geqslant_{\mathrm{M}}\left(\lambda \alpha_{1}+(1-\lambda) \alpha_{2}, \lambda \alpha_{2}+(1-\lambda) \alpha_{1}\right)^{\mathrm{T}}. $ |
由n=2时的结论可得
| $ \begin{aligned} & \left(\lambda \alpha_{1}+(1-\lambda) \alpha_{2}\right) X_{1}+\left(\lambda \alpha_{2}+\right. \\ & \left.(1-\lambda) \alpha_{1}\right) X_{2} \geqslant_{\mathrm{SSD}} \alpha_{1} X_{1}+\alpha_{2} X_{2} \end{aligned} $ |
若
| $ \begin{aligned} & \left(\alpha_{1}, \alpha_{2}\right)^{\mathrm{T}} /\left(1-\sum\limits_{i=3}^{n} \alpha_{i}\right) \geqslant_{\mathrm{M}}\left(\lambda \alpha_{1}+\right. \\ & \left.(1-\lambda) \alpha_{2}, \lambda \alpha_{2}+(1-\lambda) \alpha_{1}\right)^{\mathrm{T}} /\left(1-\sum\limits_{i=3}^{n} \alpha_{i}\right). \end{aligned} $ |
再由n=2时的结论得
| $ \begin{aligned} & {\left[\left(\lambda \alpha_{1}+(1-\lambda) \alpha_{2}\right) X_{1}+\left(\lambda \alpha_{2}+\right.\right.} \\ & \left.\left.(1-\lambda) \alpha_{1}\right) X_{2}\right] /\left(1-\sum\limits_{i=3}^{n} \alpha_{i}\right) \\ & \geqslant_{\mathrm{SsD}}\left(\alpha_{1} X_{1}+\alpha_{2} X_{2}\right) /\left(1-\sum\limits_{i=3}^{n} \alpha_{i}\right). \end{aligned} $ |
由于具有占优关系关于正的伸缩变换封闭,因此有
| $ \begin{aligned} & \left(\lambda \alpha_{1}+(1-\lambda) \alpha_{2}\right) X_{1}+\left(\lambda \alpha_{2}+\right. \\ & \left.(1-\lambda) \alpha_{1}\right) X_{2} \geqslant_{\mathrm{SSD}} \alpha_{1} X_{1}+\alpha_{2} X_{2}. \end{aligned} $ |
另一方面,占优关系关于平移变换也封闭,即
| $\left(\lambda \alpha_{1}+(1-\lambda) \alpha_{2}\right) X_{1}+\left(\lambda \alpha_{2}+(1-\lambda) \alpha_{1}\right) X_{2}+ \\ \sum\limits_{i=3}^{n} \alpha_{i} x_{i} \geqslant_{\mathrm{SSD}} \alpha_{1} X_{1}+\alpha_{2} X_{2}+\sum\limits_{i=3}^{n} \alpha_{i} x_{i}. $ |
因此,对任意的U∈ U2,
| $ \begin{aligned} \mathrm{E}\left[U\left(\sum\limits_{i=1}^{n} \gamma_{i} X_{i}\right)\right] \\ =\mathrm{E}\left\{\mathrm { E } \left[U \left(\left(\lambda \alpha_{1}+(1-\lambda) \alpha_{2}\right) X_{1}+\right.\right.\right. \end{aligned} $ |
| $ \begin{aligned} \left.\left.\left.\left(\lambda \alpha_{2}+(1-\lambda) \alpha_{1}\right) X_{2}+\sum\limits_{i=3}^{n} \alpha_{i} X_{i}\right) \mid X_{3}, \cdots, X_{n}\right]\right\}\\ \geqslant \mathrm{E}\left\{\mathrm{E}\left[U\left(\alpha_{1} X_{1}+\alpha_{2} X_{2}+\sum\limits_{i=3}^{n} \alpha_{i} X_{i}\right) \mid X_{3}, \cdots, X_{n}\right]\right\} \\ =\mathrm{E}\left[U\left(\sum\limits_{i=1}^{n} \alpha_{i} X_{i}\right)\right] \end{aligned} $ |
令
| $ \mathrm{E}\left[U\left(\sum\limits_{i=1}^{n} k_{i} X_{i}\right)\right] \geqslant \mathrm{E}\left[U\left(\sum\limits_{i=1}^{n} \gamma_{i} X_{i}\right)\right]. $ |
重复上面推导过程,可得
| $ \begin{gathered} \mathrm{E}\left[U\left(\sum\limits_{i=1}^{n} \beta_{i} X_{i}\right)\right] \geqslant \cdots \geqslant \mathrm{E}\left[U\left(\sum\limits_{i=1}^{n} k_{i} X_{i}\right)\right] \geqslant \\ \mathrm{E}\left[U\left(\sum\limits_{i=1}^{n} \alpha_{i} X_{i}\right)\right] . \end{gathered} $ |
再次利用引理1.1,有
利用引理3.4,可以得到如下定理3.3。
定理3.3 (X1, …,Xn)和(T1, …,Tn)是2列随机变量,令
| $ \sum\limits_{i=1}^{n} \beta_{i} X_{i} \mathrm{e}^{-\delta T_{i}} \geqslant_{\mathrm{SSD}} \sum\limits_{i=1}^{n} \alpha_{i} X_{i} \mathrm{e}^{-\delta T_{i}}. $ |
定理3.3要求联合密度函数是排列增的。下面的定理3.4表明,在可交换条件下,定理3.3的结论仍然成立。
定理3.4 设(X1, T1), …,(Xn, Tn)为1列可交换随机向量,向量αn=(α1, …,αn)T和βn=(β1, …,βn)T满足
| $ \begin{aligned} & \sum\limits_{i=1}^{n} \beta_{i} X_{i} \mathrm{e}^{-\delta T_{i}} \geqslant_{\text {SSD }} \sum\limits_{i=1}^{n} \alpha_{i} X_{i} \mathrm{e}^{-\delta T_{i}} , \\ & \sum\limits_{i=1}^{n} \alpha_{i} X_{i} \mathrm{e}^{-\delta T_{i}} \geqslant_{\text {RSSD}} \sum\limits_{i=1}^{n} \beta_{i} X_{i} \mathrm{e}^{-\delta T_{i}}. \end{aligned} $ |
证明 因
| $ \begin{aligned} & \boldsymbol{T}_{1}=\lambda \boldsymbol{I}+(1-\lambda) \boldsymbol{Q}_{1}=\left(\begin{array}{lll} \lambda & & \\ & \ddots & \\ & & \lambda \end{array}\right)+ \\ & (1-\lambda)\left(\begin{array}{lllll} 0 & 1 & & & \\ 1 & 0 & & & \\ & & 1 & & \\ & & & \ddots & \\ & & & & 1 \end{array}\right)= \\ & \left(\begin{array}{ccccc} \lambda & 1-\lambda & & & \\ 1-\lambda & \lambda & & & \\ & & 1 & & \\ & & & \ddots & \\ & & & & 1 \end{array}\right), \end{aligned} $ |
其中1/2≤λ≤1。令
| $ \begin{aligned} \mathrm{E} & {\left[U\left(\sum\limits_{i=1}^{n} \gamma_{i} X_{i} \mathrm{e}^{-\delta T_{i}}\right)\right] } \\ = & \mathrm{E}\left\{U \left[\left(\lambda \alpha_{1}+(1-\lambda) \alpha_{2}\right) X_{1} \mathrm{e}^{-\delta T_{1}}+\right.\right. \\ & \left.\left.\left(\lambda \alpha_{2}+(1-\lambda) \alpha_{1}\right) X_{2} \mathrm{e}^{-\delta T_{2}}+\alpha_{3} X_{3} \mathrm{e}^{-\delta T_{3}}+\cdots+\alpha_{n} X_{n} \mathrm{e}^{-\delta T_{n}}\right]\right\} \\ = & \mathrm{E}\left\{U\left[\lambda\left(\alpha_{1} X_{1} \mathrm{e}^{-\delta T_{1}}+\alpha_{2} X_{2} \mathrm{e}^{-\delta T_{2}}+\cdots+\alpha_{n} X_{n} \mathrm{e}^{-\delta T_{n}}\right)\right]+\right. \\ & \left.\left.(1-\lambda)\left(\alpha_{2} X_{1} \mathrm{e}^{-\delta T_{1}}+\alpha_{1} X_{2} \mathrm{e}^{-\delta T_{2}}+\cdots+\alpha_{n} X_{n} \mathrm{e}^{-\delta T_{n}}\right)\right]\right\} \\ \geqslant & \lambda \mathrm{E}\left[U\left(\alpha_{1} X_{1} \mathrm{e}^{-\delta T_{1}}+\alpha_{2} X_{2} \mathrm{e}^{-\delta T_{2}}+\cdots+\alpha_{n} X_{n} \mathrm{e}^{-\delta T_{n}}\right)\right]+ \\ & (1-\lambda) \mathrm{E}\left[U\left(\alpha_{2} X_{1} \mathrm{e}^{-\delta T_{1}}+\alpha_{1} X_{2} \mathrm{e}^{-\delta T_{2}}+\cdots+\alpha_{n} X_{n} \mathrm{e}^{-\delta T_{n}}\right)\right] \end{aligned} $ |
| $ \begin{aligned} = & \lambda \mathrm{E}\left[U\left(\alpha_{1} X_{1} \mathrm{e}^{-\delta T_{1}}+\alpha_{2} X_{2} \mathrm{e}^{-\delta T_{2}}+\cdots+\alpha_{n} X_{n} \mathrm{e}^{-\delta T_{n}}\right)\right]+ \\ & (1-\lambda) \mathrm{E}\left[U\left(\alpha_{1} X_{1} \mathrm{e}^{-\delta T_{1}}+\alpha_{2} X_{2} \mathrm{e}^{-\delta T_{2}}+\cdots+\alpha_{n} X_{n} \mathrm{e}^{-T_{n}}\right)\right] \\ = & \mathrm{E}\left[U\left(\sum\limits_{i=1}^{n} \alpha_{i} X_{i} \mathrm{e}^{-\delta T_{i}}\right)\right] \end{aligned} $ |
其中:第1个不等号由Jensen不等式得到,第3个等号是由于(X1, T1)和(X2, T2)可交换。再令
| $\mathrm{E}\left[U\left(\sum\limits_{i=1}^{n} k_{i} X_{i} \mathrm{e}^{-\delta T_{i}}\right)\right] \geqslant \mathrm{E}\left[U\left(\sum\limits_{i=1}^{n} \gamma_{i} X_{i} \mathrm{e}^{-\delta T_{i}}\right)\right]. $ |
重复上面推导过程,可得
| $\mathrm{E}\left[U\left(\sum\limits_{i=1}^{n} \beta_{i} X_{i} \mathrm{e}^{-\delta T_{i}}\right)\right] \geqslant \cdots \geqslant \mathrm{E}\left[U\left(\sum\limits_{i=1}^{n} k_{i} X_{i} \mathrm{e}^{-\delta T_{i}}\right)\right]$\geqslant \mathrm{E}\left[U\left(\sum\limits_{i=1}^{n} \alpha_{i} X_{i} \mathrm{e}^{-\delta T_{i}}\right)\right]. $ |
因此成立
随机变量可交换条件下,定理3.4揭示,风险偏好型决策者更偏好以超优向量构成的投资组合,而风险厌恶型决策者更偏好以被超优向量构成的投资组合。
定理3.4要求(X1, T1), …,(Xn, Tn)为1列可交换随机向量。若舍弃可交换的条件,定理结论是否仍然成立?答案是未必的。考虑n=2的情形,设向量(X1, T1)与向量(X2, T2)对应的分布为
| $ \begin{aligned} & X_{1}=\mathrm{e}^{0.5 Z+0.3}, X_{2}=\mathrm{e}^{0.8 Z+0.4}, Z \sim N(0, 1), \\ & T_{i} \sim U(1, 3), i=1, 2 \end{aligned} $ |
其中X1, X2, T1, T2相互独立。显然(X1, T1), (X2, T2)不满足可交换条件。对于随机变量

|
Download:
|
|
图 1 |
|
为验证

|
Download:
|
|
图 2 |
|
还可以考虑
| $ H_{2}(x)=\int_{x}^{\infty}\left(F_{W_{1}}(u)-F_{W_{2}}(u)\right) \mathrm{d} u \geqslant 0 $ |
是否始终成立。图 3给出H2(x)的图像,显然可见H2(x)始终非负,故
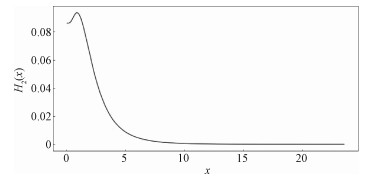
|
Download:
|
|
图 3 |
|
若考虑
| $\begin{aligned} & X_{1}=\mathrm{e}^{0.6 Z+0.6}, \quad X_{2}=\mathrm{e}^{0.8 Z+0.4}, Z \sim N(0, 1), \\ & T_{i} \sim U(1, 3), \quad i=1, 2. \end{aligned} $ |
其中X1, X2, T1, T2相互独立。易知(X1, T1), (X2, T2)仍不满足可交换条件,权重仍然取为W1 =(0.9, 0.1)T和W2 =(0.7, 0.3)T。图 4给出此时H2(x)的图像。易见H2(x)并非始终是非负的,故
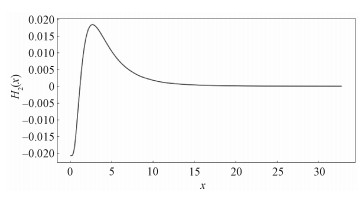
|
Download:
|
|
图 4 |
|
由上述2个例子可以得出,若舍弃可交换的条件,定理3.4的2个结论都有可能不成立。因此,可交换的条件不能轻易舍去。
4 结论与展望本文先在单笔投资的情形下,考虑利率贴现模型分别按一阶随机占优序、二阶随机占优序、风险偏好型随机占优序递减时,投资额X、投资周期T和折扣率δ间应满足的占优条件。随后,当组合系数按超优序递减时,分别在独立同分布、联合密度函数排列增、可交换3种情形下,讨论投资组合情况下的利率贴现模型按二阶随机占优序、风险偏好型随机占优序递减的充分条件。所得结果为不同类型风险偏好投资者的决策选择,具有一定的参考意义。
本文研究建立在随机变量均为非负的假设上,但是收益值为负也具有经济学意义。若是收益取值范围并不局限于正半区间,基于贴现意义下随机占优关系是否依旧可以得到?此问题可作进一步探究。另外,本文得到的结论是基于一阶随机占优序、二阶随机占优序以及风险偏好型随机占优序,但是随机占优的类型并不局限于此,还有三阶随机占优序、几乎随机占优序等等,对这些占优序,文中定理的条件和结论又如何变化?也值得进一步思考。值得一提的是,本文第3节假设投资次数n是常数,若投资次数是随机的,则总投资贴现值是各次贴现的随机和,感兴趣的读者可参阅文献[22]予以考虑。
| [1] |
Goovaerts M J, Dhaene J, de Schepper A. Stochastic upper bounds for present value functions[J]. The Journal of Risk and Insurance, 2000, 67(1): 1-14. Doi:10.2307/253674 |
| [2] |
Hua L, Cheung K C. Stochastic orders of scalar products with applications[J]. Insurance: Mathematics and Economics, 2008, 42(3): 865-872. Doi:10.1016/j.insmatheco.2007.10.004 |
| [3] |
Zhuang W W, Chen Z J, Hu T Z. Optimal allocation of policy limits and deductibles under distortion risk measures[J]. Insurance: Mathematics and Economics, 2009, 44(3): 409-414. Doi:10.1016/j.insmatheco.2008.11.012 |
| [4] |
Asmussen S, Christensen B J, Taksar M. Portfolio size as function of the premium: modelling and optimization[J]. Stochastics, 2013, 85(4): 575-588. Doi:10.1080/17442508.2013.797426 |
| [5] |
Jeon J, Park K. Optimal retirement and portfolio selection with consumption ratcheting[J]. Mathematics and Financial Economics, 2020, 14(3): 353-397. Doi:10.1007/s11579-020-00259-w |
| [6] |
Agudelo G, Franco L, Saona P. Actuarial model for estimating the optimum rate of return of a joint-and-survivor annuity portfolio[J]. Journal of Intelligent & Fuzzy Systems, 2021, 40(2): 1751-1759. Doi:10.3233/jifs-189182 |
| [7] |
Ranjbar M, Nasiri M M, Torabi S A. Multi-mode project portfolio selection and scheduling in a build-operate-transfer environment[J]. Expert Systems With Applications, 2022, 189: 116-134. Doi:10.1016/j.eswa.2021.116134 |
| [8] |
廖长高, 李贤平, 徐萍. 关于CIR模型中即期利率的条件密度及贴现债券定价[J]. 应用数学, 2002, 15(S1): 81-84. |
| [9] |
Hadar J, Russell W. Rules for ordering uncertain prospects[J]. The American Economic Review, 1969, 59(1): 25-34. |
| [10] |
Hanoch G, Levy H. The efficiency analysis of choices involving risk[J]. The Review of Economic Studies, 1969, 36(3): 335-346. Doi:10.2307/2296431 |
| [11] |
Rothschild M, Stiglitz J E. Increasing risk: I. A definition[J]. Journal of Economic Theory, 1970, 2(3): 225-243. Doi:10.1016/0022-0531(70)90038-4 |
| [12] |
Hammond J S Ⅲ. Simplifying the choice between uncertain prospects where preference is nonlinear[J]. Management Science, 1974, 20(7): 1047-1072. Doi:10.1287/mnsc.20.7.1047 |
| [13] |
Meyer J. Second degree stochastic dominance with respect to a function[J]. International Economic Review, 1977, 18(2): 477-487. Doi:10.2307/2525760 |
| [14] |
Hadar J, Russell W R. Stochastic dominance and diversification[J]. Journal of Economic Theory, 1971, 3(3): 288-305. Doi:10.1016/0022-0531(71)90024-X |
| [15] |
Tesfatsion L. Stochastic dominance and the maximization of expected utility[J]. The Review of Economic Studies, 1976, 43(2): 301-315. Doi:10.2307/2297326 |
| [16] |
Li C K, Wong W K. Extension of stochastic dominance theory to random variables[J]. RAIRO-Operations Research, 1999, 33(4): 509-524. Doi:10.1051/ro:1999100 |
| [17] |
Guo X, Wong W K. Multivariate stochastic dominance for risk averters and risk seekers[J]. RAIRO-Operations Research, 2016, 50(3): 575-586. Doi:10.1051/ro/2016026 |
| [18] |
Levy H. Stochastic dominance: investment decision making under uncertainty[M]. 3rd ed. New York, NY: Springer New York, 2016. Doi:10.1007/978-3-319-21708-6
|
| [19] |
Ma C. On peakedness of distributions of convex combinations[J]. Journal of Statistical Planning and Inference, 1998, 70(1): 51-56. Doi:10.1016/S0378-3758(97)00178-X |
| [20] |
Shaked M, Shanthikumar J G. Stochastic orders[M]. New York, NY: Springer New York, 2007. Doi:10.1007/978-0-387-34675-5
|
| [21] |
Egozcue M, Wong W K. Gains from diversification on convex combinations: a majorization and stochastic dominance approach[J]. European Journal of Operational Research, 2010, 200(3): 893-900. Doi:10.1016/j.ejor.2009.01.007 |
| [22] |
高振龙, 胡晓予. 二重随机序列随机和的重对数律[J]. 中国科学院研究生院学报, 2011, 28(4): 424-430. Doi:10.7523/j.issn.2095-6134.2011.4.002 |
 2024, Vol. 41
2024, Vol. 41 


