视频合成孔径雷达(video synthetic aperture radar，ViSAR)^[1]是一种高帧率、高分辨率的SAR成像模式，它在特定区域动态监测、运动目标检测与跟踪方面具有突出优势。运动目标检测是SAR领域的一个重要研究方向^[2]，在发展初期，单通道运动目标检测方法主要利用动目标与静止目标多普勒频率和多普勒调频率的差异设计滤波器区分二者，如频率检波、前置滤波方法等^[3-4]。因此该类方法只对偏离杂波谱的动目标有效，最小可检测速度较大，无法检测出淹没在杂波谱的目标。随后，基于杂波抑制的多通道方法被提出，常见的方法有：偏置相位中心天线(displaced phase center antenna，DPCA)技术、沿迹干涉(along track interferometry，ATI)技术以及空时自适应处理(space-time adaptive processing，STAP)技术^[5-7]，该类方法被广泛应用在复杂背景下的动目标检测场景。然而，DPCA和ATI技术的实际检测性能受基线长度限制，STAP技术无法避免系统的高复杂度和高运算量，且三者都存在检测盲速问题^[8-9]。随着ViSAR技术发展，基于图像域的运动目标检测方法(如各种背景建模方法^[10-11])被广泛研究，该类方法不存在检测盲速，且能实现对特定区域的动态观测，便于分析各目标的运动状态和轨迹跟踪。

近年来，矩阵分解方法被广泛用于运动目标检测^[12-17]，其中最具有代表性的便是鲁棒主成分分析(robust principal component analysis，RPCA)。Yan等^[18]将RPCA方法引入SAR-GMTI(ground moving target indication)中，利用补偿相位后的多通道数据构建观测矩阵，通过低秩稀疏分解(low-rank sparse decomposition，LRSD)方法提取前景目标，实验结果证明在非均匀场景下，该方法比STAP技术更具有检测优势。但该方法检测性能受制于通道均衡的精度，同时基础RPCA模型的分解能力有限，运动目标提取并不精确。在ViSAR方面，Zhang等^[19]优化了LRSD的参数设置，提升了矩阵分解性能，并基于未知统计分布的前景图像提出新的检测器。但该方法只应用了基础的RPCA模型，仅将每个像素视为独立的点，没有考虑其空间存在的结构性规律，这样会导致零散强噪点被误判为运动目标。此外，该方法并未考虑地物后向散射系数的空变性产生的动态背景问题。因而并不适用于包含动态背景、强散射点等因素的复杂场景下的检测任务。

综上，为应对复杂地物场景下的检测任务，本文提出一种新的ViSAR运动目标检测方法。首先，提出一种新的低秩稀疏模型，它拥有更优的矩阵分解性能，能有效区分离散噪点与微小目标，配合更优的低秩求解器以进一步提升矩阵分解性能。而后，针对动态背景问题提出基于复合聚类分割的运动轨迹区域提取方法，有效去除虚警的同时缩小检测范围。最后，基于运动轨迹区域采用均值背景建模差分方法完成动目标检测。该方法能将复杂场景转化为简单场景，从而具有较好的鲁棒性与检测性能。

1 ViSAR动目标检测算法

在ViSAR中，多帧连续图像序列的背景具有高度相关性，属于低秩的静态地物。同时，SAR图像中的运动目标占据较少的像素点，绝大部分运动目标的灰度值高于静态背景，运动目标是稀疏可辨的。虽然SAR图像中地物具有散射特征的各向异性，但观测角度在一定变化范围内散射特性可以近似认为稳定^[19]，所以ViSAR图像序列同样适配RPCA模型。这样的图像序列可以由聚束模式或圆迹模式获取。考虑复杂场景下检测时存在动态背景(如微动的物体、由散射各向异性导致的场景变化)干扰，可以将观测矩阵M具体分解为低秩静态背景L、稀疏前景S、稀疏动态背景D及背景噪声N。

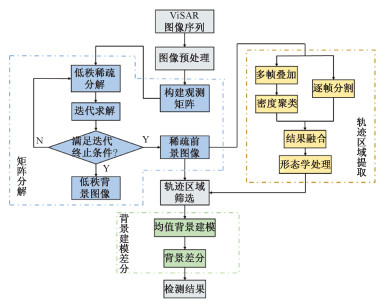
矩阵分解所得稀疏前景即为理论上的运动目标，但实际操作中分解效果受诸多因素影响导致检测效果不理想，因而借鉴两步式RPCA“块稀疏”思想，提出使用复合聚类分割方法从前景矩阵中获取动目标区域，并在该区域下使用背景建模方法完成检测，消除多余干扰。其具体步骤如下。算法流程图如图 1所示。

1) 使用改进模型进行稀疏低秩分解获得前景图像。

2) 利用复合聚类分割方法提取运动目标区域，提取结果进行形态学优化处理。

3) 基于提取区域进行背景建模差分完成检测。

1.1 改进的RPCA模型及求解

基础的RPCA模型凸松弛后求解的优化问题如下：

$ \begin{aligned} \min _{L, S}\|\boldsymbol{L}\| * & +\lambda\|\boldsymbol{S}\|_1, \\ \text { s.t. } \quad \boldsymbol{M} & =\boldsymbol{L}+\boldsymbol{S} . \end{aligned} $

(1)

式中: $\|\boldsymbol{L}\|_*$表示低秩矩阵$\boldsymbol{L}$的核范数, $\|\boldsymbol{S}\|_1$表示稀疏矩阵$\boldsymbol{S}$的$l_1$范数。关于参数$\lambda$, 通常取为$\lambda=1 / \sqrt{\max (m, n)}, m$和$n$为观测矩阵的行数和列数。然而, 这样的模型存在一定缺陷: 首先, 它将每个像素点视为各自独立, 并没有考虑相互间的空间结构规律以及时间连续性, 这可能会破坏数据本身的时空结构; 其次, 该模型只适用于简单的场景分解, 针对复杂场景的鲁棒性差^[12]。

因此，文中引入结构稀疏范数补充模型以捕捉数据空间结构特性。定义T(S)为结构稀疏范数^[20]，它在每一帧图像上设计3×3的滑动窗口，并遍历全部像素点，计算全部窗口数据的l_∞范数之和作为稀疏度衡量结果，其表达式为

$ T(\boldsymbol{S})=\sum\limits_{j=1}^p \sum\limits_{g \in G}\left\|s_g^j\right\|_{\infty} . $

(2)

式中：g是滑动窗口所覆盖的像素点，不同位置的窗口对应g构成集合G。对相同灰度值不同分布状态的目标实验，结构稀疏范数对目标稀疏状态度量能力优于l₁范数^[20]，它能显著区分分布离散的干扰点与目标点，保证前景目标空间连续性完整。需要指出，窗口大小选择会对稀疏度量产生影响，所以该项参数设定应根据图像分辨率、目标大小及目标稀疏程度等因素设置。

本节在基础RPCA模型上改进，采用结构稀疏范数约束前景矩阵，优化稀疏度量方式，剔除离散干扰点，使得前景提取更精确。在背景的约束上仍采用核范数，但使用更优的低秩求解器OptShrink代替奇异值算子提升背景分离效果。考虑场景复杂性，在模型中增添动态背景和噪声项完善对场景的描述，以提升模型鲁棒性，改进的模型如下式

$ \begin{gathered} \min _{\boldsymbol{L, S, D,} \boldsymbol{N}}\|\boldsymbol{L}\|_*+\lambda_s T(\boldsymbol{S})+\kappa \lambda_s\|\boldsymbol{D}\|_1+\frac{1}{2}\|\boldsymbol{N}\|_F^2, \\ \text { s.t. } \quad \boldsymbol{M}=\boldsymbol{L}+\boldsymbol{S}+\boldsymbol{D}+\boldsymbol{N} . \end{gathered} $

(3)

式中, $\boldsymbol{M}$是由$p$帧$m \times n$大小图像构建的观测矩阵, 该矩阵中每一列为一帧, 即$\boldsymbol{M} \in \mathbb{R}^{m n \times p}, \boldsymbol{L}$为背景矩阵, $S$为前景矩阵, $D$为动态背景矩阵, $N$为噪声矩阵, $\|N\|_F^2$是$N$的Frobenius范数。$\lambda_s$是正则化参数, 用于平衡前景和背景间的权重, $\kappa$是调优参数, 用于调节动态背景和前景的权重。基于式(3), 构建等效无约束问题

$ \begin{gathered} \min _{\boldsymbol{L, S, D}}\|\boldsymbol{L}\|_*+\lambda_s T(S)+\kappa \lambda_s\|\boldsymbol{D}\|_1+ \\ \frac{1}{2}\|\boldsymbol{M}-\boldsymbol{L}-\boldsymbol{S}-\boldsymbol{D}\|_F^2 . \end{gathered} $

(4)

上述优化问题可以使用近端梯度方法求解^[21]，该方法中，假设目标函数可以分解为f(z)=g(z)+h(z)，其中g(z)是可微凸函数，h(z)是凸函数，则近端梯度算子可表示为

$ \operatorname{prox}_h(x)=\underset{z}{\operatorname{argmin}}\|z-x\|_F^2+h(z) . $

(5)

其迭代形式为

$ x^{k+1}=\operatorname{prox}_{h, \tau}\left(x^k-\tau^k \nabla g\left(x^k\right)\right) \text {. } $

(6)

式中: ▽为梯度算子，τ为步长。关于步长的设定，文献[22]给出了近端梯度方法的收敛条件，而在文献[23]中，作者论述了相似问题的收敛性，当步长τ < 2/3可以保证收敛。

为了让式(4) 与近端梯度法构建更直观的联系, 定义函数$h(\boldsymbol{L}, \boldsymbol{S}, \boldsymbol{D})=\|\boldsymbol{L}\| *+\lambda_s T(\boldsymbol{S})+$ $\kappa \lambda_s\|\boldsymbol{D}\|_1, g(\boldsymbol{L}, \boldsymbol{S}, \boldsymbol{D})=\frac{1}{2}\|\boldsymbol{M}-\boldsymbol{L}-\boldsymbol{S}-\boldsymbol{D}\|_F^2$, 故有目标函数$f(\boldsymbol{L}, \boldsymbol{S}, \boldsymbol{D})=g(\boldsymbol{L}, \boldsymbol{S}, \boldsymbol{D})+h(\boldsymbol{L}, \boldsymbol{S}$, $\boldsymbol{D})$。这符合使用近端梯度方法求最优解的形式, 同时$\nabla_\boldsymbol{L} g(\boldsymbol{L}, \boldsymbol{S}, \boldsymbol{D})=\nabla_\boldsymbol{S} g(\boldsymbol{L}, \boldsymbol{S}, \boldsymbol{D})=\nabla_{\boldsymbol{D}} g(\boldsymbol{L}, \boldsymbol{S}$, $\boldsymbol{D})=\boldsymbol{L}-\boldsymbol{S}-\boldsymbol{D}-\boldsymbol{M}$, 所以式(4) 求解可以分解为以下步骤:

$ \begin{aligned} & \boldsymbol{Y}^{k+1}=\boldsymbol{L}^k+\boldsymbol{S}^k+\boldsymbol{D}^k-\boldsymbol{M} \\ & \boldsymbol{L}^{k+1}=\operatorname{prox}_{\|\cdot\|_*, \tau^k}\left(\boldsymbol{L}^k-\tau^k \boldsymbol{Y}^{k+1}\right), \\ & \boldsymbol{S}^{k+1}=\operatorname{prox}_{\lambda_s T(\boldsymbol{S}), \tau^k}\left(\boldsymbol{S}^k-\tau^k \boldsymbol{Y}^{k+1}\right), \\ & \boldsymbol{D}^{k+1}=\operatorname{prox}_{\kappa \lambda_s\|\cdot\|_1, \tau^k}\left(\boldsymbol{D}^k-\tau^k \boldsymbol{Y}^{k+1}\right) . \end{aligned} $

(7)

根据文献[24]，动态背景矩阵D可以用软阈值算子近似求解。文献[25]证明了一种更为优越的低秩求解器OptShrink。本文同样采用此方式求解背景L。最后，前景矩阵S的迭代求解，根据文献[26]可以用近邻算子将其转化为二次最小费用流问题求解。故式(7)可以用下式迭代求解

$ \begin{aligned} & \boldsymbol{Y}^{k+1}=\boldsymbol{L}^k+\boldsymbol{S}^k+\boldsymbol{D}^k-\boldsymbol{M}, \\ & \boldsymbol{L}^{k+1}=\operatorname{OptShrink}_\gamma\left(\boldsymbol{L}^k-\tau^k \boldsymbol{Y}^{k+1}\right), \\ & \boldsymbol{S}^{k+1}=\operatorname{MC}_{\lambda_s, \tau^k}\left(\boldsymbol{S}^k-\tau^k \boldsymbol{Y}^{k+1}\right), \\ & \boldsymbol{D}^{k+1}=\operatorname{Soft}_{\kappa \lambda_s}\left(\boldsymbol{D}^k-\tau^k \boldsymbol{Y}^{k+1}\right) . \end{aligned} $

(8)

式中: $\operatorname{Soft}_\lambda(\cdot)$为软阈值收缩算子, 其定义为$\operatorname{Soft}_\lambda(\boldsymbol{X})=\max (|\boldsymbol{X}|-\lambda, 0) \operatorname{sgn}(\boldsymbol{X}) ; \operatorname{MC}(\cdot)$表示结构稀疏范数的求解算子, 详见文献[21]; $\operatorname{OptShrink}_\gamma(\boldsymbol{X})=\sum\limits_{i=1}^\gamma\left(-2 \frac{D_{\mu X}\left(\sigma_i\right)}{D_{\mu X}^{\prime}\left(\sigma_i\right)}\right) \boldsymbol{u}_i \boldsymbol{v}_i^{\mathrm{H}}$, 其中$\boldsymbol{X}=\sum\nolimits_i \sigma_i \boldsymbol{u}_i \boldsymbol{v}_i^{\mathrm{T}}$ (该式为奇异值分解, $\boldsymbol{X} \in \mathbb{R}^{m \times n}$); $D_\mu(x)=\int \frac{x}{x^2-t^2} \mathrm{~d} \mu(t) \times c \int \frac{x}{x^2-t^2} \mathrm{~d} \mu(t)+\frac{1-c}{x}$, $D_\mu(x)$是$D_\mu(x)$的导数, $c=\frac{\min (m, n)}{\max (m, n)}, \mu X(t)=$ $\frac{1}{q-\gamma} \sum\limits_{i=\gamma+1}^q \delta\left(t-\sigma_i\right)$是一种只有噪声奇异值的经验函数且$q=\min (m, n)$, 这里$\min (\cdot)$表示取最小值。迭代终止条件与文献[20]相同。

1.2 基于复合聚类分割的运动轨迹区域提取

经过矩阵分解可以获得包含运动目标的前景矩阵，但仍存在部分杂波干扰。矩阵分解后的分布无从得知，故CFAR检测器不再有效^[19]，并且由于动态背景灰度值与运动目标接近，基于灰度统计特性的Otsu分割方法也不再适用。受两步式RPCA中“块稀疏”思想启发，在矩阵低秩稀疏分解所得前景图像的基础上，本文提出一种复合聚类分割方法提取运动目标轨迹区域，通过标识目标运动区域，消除非标识区域产生的虚警，运动区域提取的同时缩小了检测范围，方便后续处理。具体实现如下。

首先，进行逐帧局部自适应阈值分割和多帧聚类。矩阵分解后的运动目标是稀疏的，灰度分布也是非密集的，采用局部阈值分割能有效应对这种情况。Niblack算法是一种局部分割方法，采用滑窗结构，计算窗内灰度值均值和标准差作为阈值进行判别。本文借鉴Niblack方法思想，优化阈值设定，能对目标中心点以及孤立干扰点做出有效分割。需要注意的是，此处设定的背景灰度值高于待测目标的灰度值^[27](小于阈值判定为目标)。

$ \begin{gathered} T(x, y)=m(x, y)-k \times v(x, y) \times \\ \left(1-\frac{v(x, y)}{m(x, y)}\right)-\frac{\left[m_8(x, y)-v(x, y)\right]}{l} . \end{gathered} $

(9)

式(9) 为阈值分割的判定门限。其中: $l$为选取窗口大小, $m(x, y)$表示窗内像素均值, $v(x, y)$表示窗内像素标准差, $k$是修正系数, $m_8(x, y)$是点$(x$, $y)$的8邻域均值。当位于目标中心位置时, 均值较小, 标准差较大, 故$\left(1-\frac{v(x, y)}{m(x, y)}\right)$较小, 从而提升门限, 避免背景误判。同时, 考虑一些孤立点的误判, 式(9) 最后一项引入周围像素点均值做辅助判断。当周围像素点均值较高时, 该点是背景的可能性较大, 所以应适当降低门限。将逐帧分割结果叠加记为结果1。

在多帧聚类方面，将全部前景图像叠加，使用k-means与DBSCAN(density based spatial clustering of applications with noise)结合的聚类方法。利用k-means为DBSCAN提供不同类别坐标信息，从而完成密度聚类。聚类结果记为结果2。

然后进行结果融合。先获取结果1和结果2的重叠区域坐标，而后在上述2个结果中，逐一寻找每个坐标所对应的最大连通区域，以此作为运动轨迹区域。基于局部统计特性的逐帧分割对于动态背景与目标具有良好的区分性，而基于分布特性的多帧聚类则是为了保留完整的运动轨迹区域。可将二者结果融合以获取准确的轨迹区域。

1.3 均值背景建模

低秩稀疏分解后，可以直接使用均值背景建模方法实现运动目标检测，但是会存在动态背景和强孤立点干扰。所以在均值背景建模差分前，先使用复合聚类方法建立运动轨迹区域，对前景图像进行区域筛选，框选运动目标出现的特定区域，而后对这些区域逐一使用均值背景建模，能进一步消除虚警项。

首先，对前景矩阵的运动轨迹区域计算灰度均值作为背景，然后逐帧作背景差分，设定阈值以判断是否为目标。由于矩阵分解后的动目标与背景灰度值存在明显差异，所以阈值可以简单设置为最大灰度值与最小灰度值之差的一半。

2 实验结果

本节中使用Ku波段齐鲁1号聚束模式数据生成视频图像序列验证算法有效性，该模式下方位扫描角为6°，使用0.43°的子孔径积累角对应数据产生子图像，子孔径重叠率为95 %，选取其中56帧图像序列。参数设置方面，根据经验设定结构稀疏范数滑动窗口大小为5×5，样本框l=40，修正系数k=4，调优参数κ=0.2，λ_s=$2 / \sqrt{\max (m, n)}$。同时设置对比实验证明算法优越性。

2.1 评价指标

采用正确检测数(true positives，T_P)、虚警数(false positives，F_P)、漏检数(false negatives，F_N)、准确率(precision, p)、召回率(recall, r)。准确率和召回率定义如下：

$ p=\frac{T_{\mathrm{P}}}{T_{\mathrm{P}}+F_{\mathrm{P}}} . $

(10)

$ r=\frac{T_{\mathrm{P}}}{T_{\mathrm{P}}+F_{\mathrm{N}}} . $

(11)

虚警数为错判目标数量，漏检数为漏判目标数量，正确检测数、虚警数与漏检数能直接反应目标检测准确度，准确率与召回率则能体现算法综合检测性能，指标越高代表检测性能越强。

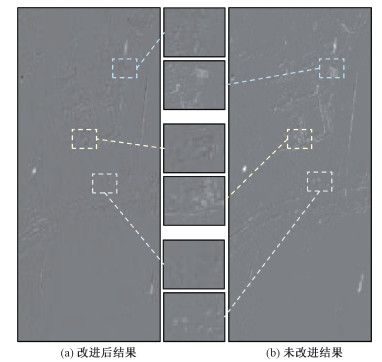
2.2 改进模型性能分析

首先对比改进前后模型的分解性能差异。分别使用改进模型与原模型对观测矩阵分解，并选取第16帧前景图像的部分区域做对比。如图 2所示，图 2(a)为改进模型的分解结果，图 2(b)为原模型的分解结果，中间小图为特定区域提取对比。直观来看，原模型分解结果保留了诸多杂波信息，这些杂波的灰度分布与目标相近，因而在后续检测会造成虚警，这点在2.4节中也有体现。理论分析上改进后的模型对于离散点具备一定辨识能力，即非目标区应该与背景的灰度分布相近并与目标区分，分解的结果上同样体现了这点，选取的几个区域中，改进模型结果更为平滑，离散干扰点少，目标与背景区分显著，更符合理论与预期。此外，使用图像方差进行量化分析，对于非目标区域，方差越低证明分解效果越好，对选取的3个区域做方差分析，改进后平均方差为23.7，未改进的平均方差为34.4，证明了改进模型分解效果的显著提升。

2.3 ViSAR数据动目标检测结果

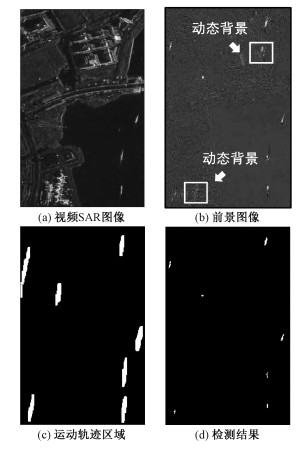
本次实验选取场景包含城市街区与部分水域以验证算法在复杂场景下的检测性能。其中水域部分背景均匀单一，属于简单场景，而城市街区背景非均匀，存在动态变化背景以及强散射点，视为复杂场景。图 3为第28帧图像检测结果，其中图 3(a)为原始场景，图 3(b)为矩阵分解后的前景图像，图 3(c)为使用多帧前景图像提取出的运动轨迹区域图，图 3(d)为均值背景建模差分后的检测结果。由实验结果可知，场景中的运动目标均可被准确检测，并且目标轮廓形状提取完整。特别是在该帧图像中出现的动态背景得到有效消除，矩阵分解后残存的一些干扰也被清除，证明了算法较好的性能。

2.4 对比实验结果

本小节中设置3组对比试验，分别为使用均值背景建模方法^[10](对照组1)、采用常规低秩稀疏分解结合密度聚类的方法(对照组2)与文献[19](对照组3)方法对相同场景检测。

图 4给出本文方法与对照组的第16、32、48帧的实验结果。将图中场景分割为两部分，原图区域①为复杂地物场景(城区)，区域②为简单场景(水域)。使用矩形框和椭圆框分别标注复杂场景和简单场景中被成功检测的运动目标。可以看到，简单场景下，4种方法都可以成功检测目标，但对照组1中，提取目标形状不算完整。在复杂场景下，对照组1虚警明显增多。所以静态背景建模方法不适用于复杂背景下的运动目标检测，一方面动态背景以及噪声干扰会产生大量虚警，另一方面差分会使得目标部分缺失。对照组2实验结果中，在3帧检测结果中均出现了诸多虚警，这是因为低秩稀疏分解对动态背景鲁棒性差，所以需要引入其他方法来消除多余干扰。对照组3中引入ATD(adaptive threshold detector)与DBSCAN方法对分解结果进一步分割，因而相较对照组2虚警目标减少，但同样无法处理动态背景的干扰。引入2.1小节评价指标对上述4种方法定量分析，检测目标总数为356，结果如表 1所示。

由表 1可知，采用低秩稀疏分解方式(对照组2、对照组3)提取运动目标有较好效果，漏检数较少，但弊端是无法消除动态背景产生的虚警问题，虚警数多；而背景建模(对照组1)方法使用背景差分，在背景提取不精确时会损失目标，同时面对动态背景也存在大量的虚警。相较而言，本文方法可将漏检和虚警情况控制在较低水平，检测精度较高。

通过上述几种方法对比，可看出本文方法在复杂背景下运动目标检测的优越性，改进的模型及优化求解方式可以获取更好的矩阵分解效果，运动轨迹区域提取不仅能消除多余干扰，同时也能用于判断目标的运动状态。

3 结束语

本文分析了使用RPCA模型分解ViSAR数据的可行性，并针对动态背景造成动目标检测的虚警问题提出解决方案，即提出一种基于稀疏低秩分解和运动轨迹区域提取的ViSAR运动目标检测算法。该算法在基础RPCA模型做出改进，引入结构稀疏范数以及噪声干扰鲁棒项来完善结构，提升模型鲁棒性及分解准确度。同时改进自适应阈值分割器，并使用复合分割方法提取运动轨迹区域消除虚警、缩小检测范围，将提取区域融入前景矩阵中，从而把复杂场景转化成简单场景，最后使用均值背景建模差分完成检测。实验证明该方法在复杂场景下具有优异的检测性能。未来会在RPCA模型中加入更多先验信息如时间连续性、轨迹信息等，使分解更加准确，以简化后续目标提取步骤，同时考虑算法运算成本，优化模型以降低算法复杂度。