2. 中国科学院空天信息创新研究院, 北京 100194
2. Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing 100194, China
雷达和通信是现代电子设备系统中最为常见的2种功能,随着人们对平台多功能需求的增加,研究者提出了雷达和通信功能共存的概念。然而,在同一平台上搭载这两种功能设备,会造成系统的体积增大、重量增加、电磁兼容性变差、资源浪费等[1-2]。为解决这些问题,相关学者提出雷达通信一体化的新概念,即通过综合设计,在同一系统平台上,通过共享天线、射频电路、信号处理、显示等硬件资源,实现雷达和通信2种功能[3]。随着电子技术、数字处理技术的发展,雷达和通信在射频前端和数字处理单元上不断接近,两者共用硬件资源已获得初步成果和应用[4]。现阶段,雷达通信一体化技术实现的关键是一体化共享波形的设计。
一体化共享波形的设计发展分为2个分支[5]:1)基于复用技术的一体化波形设计,包括时分复用[6-7]、频分复用[8-9]、码分复用[10]和空分复用[11-12]。通过时、频、码、空复用方式设计一体化波形,在实现方式上相对简单,但是从资源利用率的角度看,此类波形存在不同维度资源浪费的固有缺点[13]; 2)基于共用信号的一体化波形技术,该波形设计方法可以同时、同频、同波束地实现雷达和通信功能。根据共用信号的不同,可以把此类信号分为基于雷达信号的一体化波形[9, 14-15]和基于通信信号的一体化波形[4-5, 13, 16]。
正交频分复用(orthogonal frequency division multiplexing, OFDM)信号由于具有子载波调制灵活、频带利用率高、大时宽积等优点[17-18],在基于通信信号的一体化波形研究领域中得到广泛关注。Levanon[19]首先在雷达领域引入OFDM调制技术,其研究表明,OFDM信号应用于雷达探测,相较于传统线性调频(linear frequency modulation, LFM)信号具有更好的距离向模糊度[20]。由此看来,OFDM信号在单独实现雷达和通信功能时,可使二者均达到较好的性能。但OFDM信号作为共享信号存在一个棘手的问题,即在基于匹配滤波的合成孔径雷达(synthetic aperture radar, SAR)信号处理过程中,高随机性的通信信息、导频信息和循环前缀会导致OFDM信号的相关性能下降,进而导致二维模糊函数出现高旁瓣和伪峰[21]。为解决这一问题,目前相关学者的研究重点是寻找通信信息的编码方式,优化发射信号的互相关系数,实现距离旁瓣的抑制。例如刘永军等[4]提出采用Gold序列等对通信信息进行预调制,该方法可以一定程度上消除信息调制对模糊函数和旁瓣的影响[22-23], 但存在通信的信息速率低、扩频导致所需带宽展宽等缺点。雍萍等[1]提出将高旁瓣和伪峰外推至雷达观测窗口之外的失配滤波方法,以此兼顾雷达和通信性能,但该方法会产生主瓣信噪比损失。张霄霄等[24]针对失配滤波方法信噪比损失进行了改进。此外,还有基于加权预处理的一体化波形优化方法[16, 25],也在一定程度上实现了模糊函数旁瓣抑制。上述方法均是在传统匹配滤波方式下进行的,只能将距离旁瓣压缩到一定程度,依旧可能会存在强点目标的旁瓣淹没相邻的弱目标的情况[26];并且上述方法并没有发挥OFDM信号在通信应用中良好的抗多径性能[27]。2015年,Zhang和Xia[28]提出基于循环前缀(cyclic prefix, CP)的OFDM SAR非匹配滤波处理方法,在OFDM信号中加入足够长CP实现无距离单元串扰SAR成像。但该团队并没有研究此方法应用在一体化信号处理中的算法性能。
为消除OFDM一体化信号中通信信息对成像性能的影响,本文首先将基于CP的非匹配滤波成像算法应用于一体化信号的处理过程中,以避免匹配滤波的固有缺点,并通过仿真实验验证了该方法无需其他操作就可消除通信信息对成像性能的影响,且可以实现距离向超低旁瓣成像,证明了该算法在SAR通信一体化处理中具有很高的研究价值和应用前景。然后针对OFDM信号高峰均功率比的固有缺点,同时考虑到通信和成像处理过程中CP被移除,导致CP段能量浪费的问题,提出一种基于DFT预编码和CP段置零的一体化信号改进方法。该方法可以在保证通信性能的前提下,降低信号的峰均比,同时消除CP段的能量浪费。本文通过对一体化波形设计和处理方法统一优化,实现了一体化信号高性能和鲁棒性。
1 基于OFDM的一体信号模型本文讨论的SAR通信一体化工作模式是在单站收发共用天线的情况下,发射信号完成成像工作的同时,同频、同波束地完成通信数据的下传工作。
1.1 OFDM一体化共享信号模型OFDM一体化信号采用正交多载波体制,一般信号模型为
| $ s(t)=\sum\limits_{k=0}^{N-1} S_k \exp (\mathrm{j} 2 \pi k \Delta f t), t \in[0, T], $ | (1) |
其中:N为一个OFDM符号中子载波的个数;S =[S0, S1, …, SN-1]T为一体化信号子载波的加权系数向量,且为携带通信信息的多进制数字相位调制(multiple phase shift keying, MPSK)信号;Δf为子载波频率间隔,单位Hz;T为一个OFDM符号的时长,单位s。假设OFDM信号的带宽为B,单位Hz, 则子载波个数、带宽、子载波频率间隔和符号时长之间的关系满足
| $ \Delta f=B / N=1 / T_{\text {。}} $ | (2) |
为保证通信质量和基于CP的匹配滤波算法的应用,在OFDM信号的前端加上CP。其中CP的时长为TCP,单位s,满足TCP≤T。[0, TCP)的信号与(T, T+TCP]相同, 则完整OFDM信号时长变为T+TCP。加入循环前缀后的发射信号为
| $ s(t)=\sum\limits_{k=0}^{N-1} S_k \exp \left(\mathrm{j} 2 \pi f_k t\right), t \in\left[0, T+T_{\mathrm{CP}}\right], $ | (3) |
其中:fk=fc+kΔf,fc为主载波频率,单位Hz。
上述一体化信号的整体产生方案步骤为:首先,二进制串行通信数据经过串并转换,变成并行传输数据,经过MPSK调制后,通过快速傅里叶逆变换(inverse fast Fourier transform, IFFT)变换完成OFDM调制;然后加入CP,经过并串转换,变成串行数据;最后经过DAC进入射频段处理。
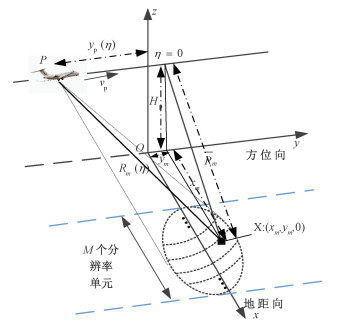
1.2 OFDM一体化信号SAR回波模型利用1.1节中发射信号模型和图 1所示的单站条带SAR正侧视几何结构图完成回波建模。假设测绘范围内存在M个距离向分辨率单元,其中O点为方位向时刻为零的点;SAR通信联合载体所在位置P点坐标可以表示为:(0, yp(η), Hp),其沿方位向的运动速度为vp,则yp(η)=vpη,η为雷达所在位置偏离O点的方位向时间,Hp为目标与载体之间的相对高度;目标所在位置X点坐标为: (xm, ym, 0),处在第m个距离分辨率单元处。其中m=0, 1, 2, …, M-1。根据图 1中几何关系得到目标到SAR接收端的斜距为
|
Download:
|
| 图 1 单站条带SAR正侧视几何结构图 Fig. 1 Front and side view geometry diagram of single-station strip SAR | |
| $ R_m(\eta)=\sqrt{\overline{R_m^2}+\left(y_p(\eta)-y_m\right)^2}, $ | (4) |
其中:
| $ R_m(\eta)=\sqrt{x_m^2+H_p^2+\left(v_p \eta-y_m\right)^2} . $ | (5) |
一体化信号经过发射、目标后向散射,被SAR天线接收,然后经过相干解调,去载波后的基带回波信号为
| $ \begin{gathered} r(t, \eta)=\left\{g_m \exp \left(-\mathrm{j} 4 \pi f_{\mathrm{c}} \frac{2 R_m(\eta)}{c}\right) \times\right. \\ \left.s\left(t-\frac{2 R_m(\eta)}{c}\right)+w(t, \eta)\right\}= \\ \left\{g_m \exp \left(-\mathrm{j} 4 \pi f_{\mathrm{c}} \frac{2 R_m(\eta)}{c}\right) \times\right. \\ \left.\sum\limits_{k=0}^{N-1} S_k \exp \left(\mathrm{j} 2 \pi k \Delta f\left(t-\frac{2 R_m(\eta)}{c}\right)\right)+w(t, \eta)\right\}, \\ t \in\left[\frac{2 R_0(\eta)}{c}, \frac{2 R_{M-1}(\eta)}{c}+T+T_{\mathrm{CP}}\right], \end{gathered} $ | (6) |
其中:gm为位于第m个距离单元处的目标的雷达散射截面系数(radar cross section, RCS);t为快时间,单位s;η为慢时间,单位s;Rm(η)为η时刻目标所在位置与SAR接收端的距离,单位m;c为光速,值为3×108 m/s;w(t, η)为接收噪声。
这里,借助文献[28]中的近似关系式:当成像条带处于远区时,存在
| $ R_m(\eta) \approx R_0(\eta)+m \rho, m=0, 1, \cdots, M-1, $ | (7) |
其中:R0(η)为在方位时刻η处第1个距离单元的斜距;ρ=c/2B为距离向分辨率,距离向采样率定为OFDM信号的带宽B,则采样周期Ts=1/B。如此得到
| $ \begin{gathered} t-\frac{2 R_m(\eta)}{c}=t-\frac{2 R_0(\eta)}{c}-\frac{2 m \rho}{c}= \\ t-t_0-m T_{\mathrm{s}}{.} \end{gathered} $ | (8) |
由于t0为固定的时刻,因此对接收信号延迟t0后采样。把式(8)和t=iTs代入式(6),即得到离散化的回波信号
| $ \begin{gathered} r_i=\sum\limits_{m=0}^{M-1} g_m \exp \left(-\mathrm{j} 4 \pi f_c \frac{2 R_m(\eta)}{c}\right) s_{i-m}+w_i, \\ i=0, 1, \cdots, N+2 M-3, \end{gathered} $ | (9) |
式(9)中i的取值范围可根据t的取值范围确定。结合式(7)和式(8),式(6)中t的取值范围可改写为t∈[t0, t0+(M-1)Ts+T+TCP]。设插入的循环前缀长度为M-1,根据式(2)可得T+TCP=(N+M-1)Ts。延迟t0后得到时域范围为t∈(0, (N+2M-2)Ts],从每个Ts的中间时刻进行采样,得到N+2M-2个采样点,则i=0, 1, …, N+2M-3。
至此,就完成了SAR回波建模。
2 基于非匹配滤波的一体化信号距离向压缩处理在SAR成像过程中,不同距离分辨单元之间的干扰与通信上的多径效应类似,且基于匹配滤波的成像算法在一体化信号处理中存在固有弊端。基于此,本文将基于CP的OFDM SAR非匹配滤波成像算法[28]应用于OFDM一体化信号中。该算法在距离向采用快速傅里叶变换(fast fourier transform, FFT)非匹配滤波的方式,从根源上避免了匹配滤波算法下通信信号对二维模糊函数的影响。
2.1 算法描述该算法主要目的就是从回波数据中准确地估计出测绘带中不同距离向目标散射体的雷达散射系数gm值。算法应用中需要注意的是CP的长度和距离向分辨率单元个数需满足:
| $ L_{\mathrm{CP}} \geqslant(M-1), $ | (10) |
其中:LCP为CP长度,M为测绘带内距离向分辨率单元个数。本文研究均在LCP=M-1的情况下开展。
一体化信号的SAR回波处理过程可分为以下4步:
1) 去CP。由通信对OFDM信号的处理可知,可以通过去除CP来消除多径效应影响,我们也借鉴这种原理,去除未包含全部距离向回波能量的部分。因此,在处理之前首先把回波信号中的前M-1和后M-1个采样点移除。根据式(9)可以得出移除循环前缀后的离散回波信号为
| $ \begin{gathered} r_i=\sum\limits_{m=0}^{M-1} g_m \exp \left(-\mathrm{j} 4 \pi f_c \frac{2 R_m(\boldsymbol{\eta})}{c}\right) s_{i-m}+w_i , \\ i=M-1, M, \cdots, N+M-2 , \end{gathered} $ | (11) |
令
| $ \begin{gathered} r_i=\sum\limits_{m=0}^{M-1} d_m s_{i-m}+w_i, \\ i=M-1, M, \cdots, N+M-2, \end{gathered} $ | (12) |
即得到r=[rM-1, rM,…,rN+M-2]T。
2) 距离向FFT。移除循环前缀后对接收回波数据r进行N点FFT变换,得到
| $ \begin{gathered} R_k=\frac{1}{\sqrt{N}} \sum\limits_{i=0}^{N-1} r_{i+M-1} \exp \left(\frac{-\mathrm{j} 2 \pi k i}{N}\right)=D_k S_k^{\prime}+W_k, \\ k=0, 1, \cdots, N-1, \end{gathered} $ | (13) |
其中:S′=[S′0, S′1, …,S′N-1]T是去掉CP的发射信号s′=[sM-1, sM,…,sN+M-2]T通过N点FFT得到的;Wk为噪声的傅里叶变换; Dk为dm的N点FFT变换,可以表示为
| $ D_k=\sum\limits_{m=0}^{M-1} d_m \exp \left(-\frac{\mathrm{j} 2 \pi m k}{N}\right), k=0, 1, \cdots, N-1 . $ | (14) |
3) 频域RCS参数估计。对于SAR而言,发射信号是已知的,那么回波信号所携带的通信信息也是已知的,即S′已知,进而可以根据上述频域表达式求出频域加权RCS参数估计值D′k
| $ D_k^{\prime}=\frac{R_k}{S_k^{\prime}}=D_k+\frac{W_k}{S_k^{\prime}}, k=0, 1, \cdots, N-1 . $ | (15) |
4) 距离向IFFT。在得到频域加权RCS参数估计值后,对频域估计值进行N点IFFT变换,然后取前M个值,即得到时域加权RSC估计值d′m
| $ \begin{gathered} d_m^{\prime}=\frac{1}{\sqrt{N}} \sum\limits_{k=0}^{N-1} D_k^{\prime} \exp \left(\frac{\mathrm{j} 2 \pi m k}{N}\right)=\sqrt{N} d_m+w_m^{\prime} \\ =\sqrt{N} g_m \exp \left(-\mathrm{j} 4 \pi f_{\mathrm{c}} \frac{2 R_m(\eta)}{c}\right)+w_m^{\prime}, \\ m=0, 1, \cdots, M-1 . \end{gathered} $ | (16) |
至此,基于非匹配滤波的距离向脉冲压缩完成。从理论分析的过程可知,经过第3)步的处理,该方法可以完全消除通信信息对成像性能的影响,非常适合应用于一体化信号成像。由式(16)可得出距离向RCS估计值d′m仅与本分辨率单元的真实RSC值gm有关,从而很好地消除其他分辨率单元的干扰,实现超低旁瓣成像性能。完成距离向压缩以后,即可回归到传统的SAR信号处理,完成方位向处理,包括方位向FFT、方位向距离徙动矫正、方位向压缩、方位向IFFT。
2.2 算法性能分析为验证上述算法在一体化信号中的距离向压缩效果,首先根据1.1节步骤生成所需的一体化信号,其中通信信号的调制方式为四相相移键控(quadvature phase shift keying, QPSK)。然后假设在观测区域中心位置有一点目标,在不同噪声影响的情况下,利用上述算法给出归一化距离向点目标扩展函数,具体的仿真参数如表 1所示。
|
|
表 1 仿真参数 Table 1 Simulation parameters |
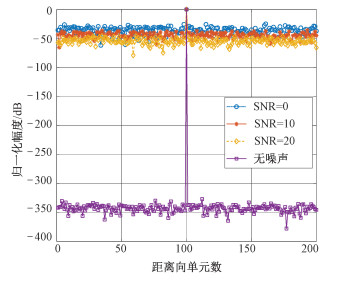
归一化距离向点目标扩展函数如图 2所示。从仿真结果中可以得出以下结论:
|
Download:
|
| 图 2 不同信噪比点目标距离向扩展函数对比 Fig. 2 Comparison of the point target range extension function under different signal-to-noise ratios | |
1) 基于非匹配滤波的OFDM一体化信号成像处理在SAR距离向成像过程中表现出超高分辨率,可以实现无距离分辨率单元干扰;
2) 使用该方法不用考虑一体化发射信号中通信信息对距离旁瓣的干扰问题,省去了对发射信号进行的各种加权和与编码操作,大大简化系统算法复杂度,同时又实现了超低旁瓣的成像效果;
3) 在信噪比(signal to noise ratio, SNR)为0 dB时,旁瓣依然保持在-30 dB以下,说明该方法在低信噪比下依然表现出较好的距离向压缩效果。
3 基于DFT预编码的一体化信号 3.1 OFDM一体化信号缺点分析通过分析可知,基于非匹配滤波的SAR信号处理技术可以使OFDM的一体化信号很好地兼容通信和SAR成像两种功能。但是上述一体化信号也存在以下缺点:
1) OFDM信号的CP个数随测绘带内距离单元数量或通信信道中多径数量增加而增加。但是在进行成像和通信处理时,这部分信号都是需要移除的,因此必然会造成能源浪费,且CP个数越多,能源浪费越严重。
2) OFDM信号具有峰均功率比(peak to average power ratio, PAPR) 值较高的问题[29],而上述一体化信号在构造的过程中并没有考虑该问题。在通信系统中,要保证信号在功放线性区或稳定在临界饱和区内,高峰均比信号必然无法充分发挥功放的高放大性能,从而导致发射信号功率下降,进而影响通信功能和雷达探测能力。本研究根据表 1仿真参数,进行了5 000组OFDM信号的PAPR值计算,此时OFDM一体化信号具有很高的峰均比值,最大PAPR值超过12 dB。一般对一体化信号的峰均比要求控制在2 dB以下。
3.2 基于DFT预编码的一体化信号设计由上述分析可知,所需的OFDM一体化信号需要满足以下几点要求:
1) 信号形式满足
2) 信号的PAPR尽量小,最好控制在2 dB以下。
3) 设计方式要简单可逆,以便通信接收端解析出通信数据。
目前,常用于通信OFDM信号中的PAPR抑制方法包括:限幅滤波法[30]、压扩法[31]、选择性映射[32-34]、部分序列传输[35]和编码类方法[36-37]等。限幅滤波类法和压扩法算法简单,但是非线性操作,会降低系统的误码率性能;选择性映射和部分序列传输操作复杂且需要额外的边带信息,会一定程度上降低信息速率;编码类方法是算法复杂度最高的算法,不适用于子载波较多的OFDM信号。并且以上所有方法均不能同时满足我们提出的要求,不适用于OFDM一体化信号。因此需要在保证通信和SAR功能兼容的前提下,寻找降低一体化信号PAPR值的方法,提高一体化信号的适用性。
为设计出符合上述要求的一体化信号,提出在原始一体化信号的产生方案IFFT之前增加原始序列补零和DFT预编码的处理过程,该方法常见于基于SC-FDMA通信体制中。信号产生及对应通信接收流程见图 3。

|
Download:
|
| 图 3 基于DFT预编码的一体化信号产生和接收方案 Fig. 3 Integrated signal generation and reception scheme based on DFT precoding | |
图 3(a)中补零步骤的具体操作为:假设子载波个数为N,有效通信信号位长度为P=N-(M-1),对MPSK调制信号进行串并转换时,每组有效信号位长度为P。然后对有效信号位后进行(M-1)位补零,得到N位原始序列。再进行DFT预编码、IFFT变换、加入循环前缀,最后得到时域信号。
由图 3可知,在进行OFDM调制之前的MPSK信号是恒模信号,直观地看,DFT预编码操作和后续的IFFT是互补可逆的,若不考虑补零操作,该系统中的时域信号就是调制信号,虽然中间有补零操作,导致最终信号并非恒模信号,但是也实现了PAPR可控,降低了原OFDM一体化信号的PAPR值。
3.3 改进的一体化信号PAPR分析该信号中包含P位恒模符号和2(M-1)个0。设恒模符号幅度为1,则得到时域信号的峰值功率为1,总功率为P,平均功率为P/(N+M-1)。设(M-1)和P之间比值a=(M-1)/P,则该信号的峰均比值GPAPR(单位dB)可以表示为
| $ \begin{aligned} & G_{\text {PAPR }}=10 \lg \left(\frac{\max \left(\left|s_n\right|^2\right)}{\mathrm{E}\left\{\left|s_n\right|^2\right\}}\right) \\ & =10 \lg \left(\frac{1}{P /(N+(M-1))}\right) \\ & =10 \lg \left(\frac{P+2(M-1)}{P}\right)=10 \lg (1+2 a) . \end{aligned} $ | (17) |
由式(17)可知,该信号的峰均比仅与参数a有关,且与a成正比,即有效信息位长度与CP位数的比值越大,信号的PAPR值越小,信号鲁棒性越好。若想把信号PAPR值控制在2 dB以下,需要把a控制在0.292以下。利用表 1的参数,设计该一体化信号,其中a=0.115 6,GPAPR为0.903 5 dB,完全符合一体化信号对PAPR的要求。同时,信号的最大峰值是固定的、已知的,可以很容易把信号功率控制在功放的线性放大区间内,由此证明所提出的波形设计方法能够很大程度地提高一体化信号的鲁棒性。
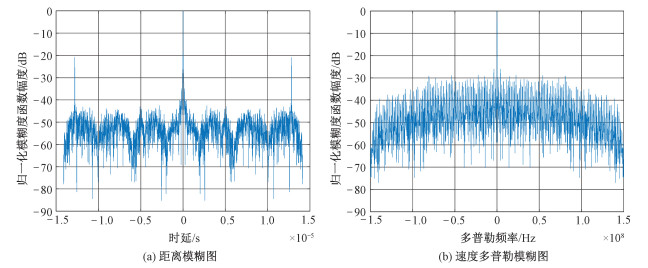
4 改进的一体化信号性能分析 4.1 成像效果分析本节利用基于非匹配滤波的一体化信号成像算法和表 1中的仿真参数,验证所提出的基于DFT预编码的一体化信号的成像效果。在传统匹配滤波框架下常以模糊函数作为评判雷达信号性能好坏的标准,因此,本实验首先给出传统匹配滤波模式下,OFDM一体化信号的模糊度函数的仿真图作为对比,见图 4。在非匹配滤波框架下,不再以模糊函数作为信号性能的评价准则,直接以成像效果作为标准。
|
Download:
|
| 图 4 OFDM一体化信号的模糊图 Fig. 4 Diagram of ambiguity function of the OFDM integrated signal | |
由图 4可以看出,传统匹配滤波框架下,OFDM一体化信号中由于CP的存在,使得模糊函数在特定时延位置处会出现较高的伪峰,且由于通信信息的相关性能较差导致模糊函数的距离旁瓣相对较高,这将严重影响雷达的成像性能。
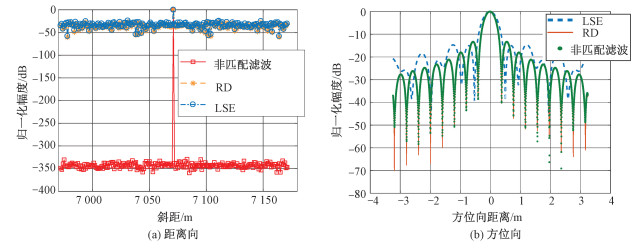
利用基于匹配滤波的距离多普勒(range doppler, RD)算法和基于最小二乘法(least square method, LSE)相位估计的方法[38-39],与非匹配滤波的成像效果进行对比分析。假设在测绘带中心有一点目标,在不考虑噪声的情况下,归一化点目标的扩展函数分布如图 5所示。不同算法的成像性能参数对比如表 2所示。
|
Download:
|
| 图 5 归一化点目标扩展函数 Fig. 5 Normalized point objective extension function | |
|
|
表 2 点目标成像指标对比表 Table 2 Point target imaging index comparison table |
由图 5(a)和表 2中距离向相关指标可以看出,所提出的一体化信号结合非匹配滤波SAR成像处理方法,其距离向旁瓣低于-320 dB,距离向峰值旁瓣比(peak-to-side lobe ratio, PSLR)和积分旁瓣比(integral side lobe ratio, ISLR)均在-310 dB以下; 而RD算法和LSE算法的距离向旁瓣在-25 dB左右,其插值后的距离向PLSR在-12.7 dB左右,ISLR在-10 dB左右。由此说明基于CP的非匹配滤波成像算法可以完全消除通信信息相关性能差所带来的高旁瓣问题,并且不必再考虑CP带来的伪峰问题,相较于传统成像算法优势明显。从图 5(b)和表 2中关于方位向的指标可以看出,基于非匹配滤波的成像处理方法在方位向与RD算法成像效果基本一致,且方位分辨率稍优于LSE算法。
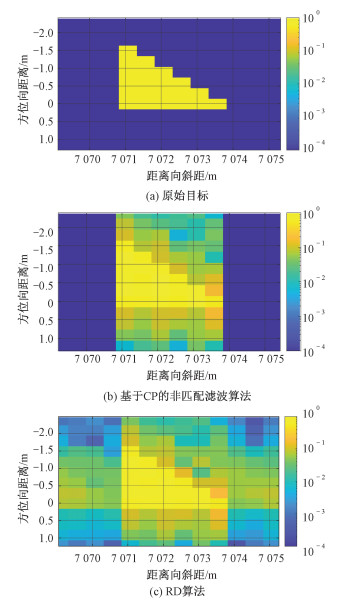
为进一步证明该一体化信号结合非匹配滤波算法的超低旁瓣性能,考虑由几个单点组成的梯形作为目标对象,其归一化成像仿真效果见图 6。原始目标散射率剖面如图 6(a)所示。通过图 6(b)和6(c)仿真对比可发现: 基于传统RD算法的成像结果中旁瓣亮斑铺满整个成像区域;但基于CP的非匹配滤波成像算法中非目标点位的距离向旁瓣的影响极小,可以忽略不记。由此可见,基于CP的非匹配滤波成像算法通过简单的FFT操作,突破了传统匹配滤波算法中通信信息对SAR成像质量的制约,消除了一体化信号中通信信息对成像的影响,实现了一体化信号的高质量成像。
|
Download:
|
| 图 6 一体化信号不同算法的成像效果对比 Fig. 6 Comparison of imaging effects of different algorithms of integrated signal | |
本小节分析在同时同频同空域一体化工作模式下,该一体化信号的通信速率和误码率性能。
首先根据信号的格式和构造方法可计算该信号的最大信息速率。由表 1的仿真参数可知,一个OFDM信号包含1 920个子载波,其中有效信息位长度为P=(N-M+1)=1 721,意味着一个OFDM符号可以承载1 721个QPSK符号,一个OFDM符号的信息承载量为
| $ C_{\text {OFDM }}=P \times 2=3442 \mathrm{bit} . $ | (18) |
一个OFDM信号的时长Ts为14.12 μs,脉冲重复频率(pulse repetition frequency, PRF)为1 kHz,则脉冲占空比D为
| $ D=T_{\mathrm{s}} \times \mathrm{PRF}=1.412 \% . $ | (19) |
考虑1/4的导频损失,因此可以得出通信速率为
| $ C=C_{\text {OFDM }} \times \mathrm{PRF} \times\left(1-\frac{1}{4}\right)=2.5815 \mathrm{Mbit} / \mathrm{s} . $ | (20) |
若循环前缀数、PRF和带宽保持不变,把子载波频率间隔缩小到15 kHz,子载波个数增加为
| $ N=B / \Delta f=10000 . $ | (21) |
一个OFDM符号的信息承载量增加为
| $ C_{\text {OFDM }}=(N-M+1) \times 2=19 602 \text { bit. } $ | (22) |
一个OFDM信号的时长增加为
| $ T+T_{\text {CP }}=(N+M-1) / B=67.9933 {\rm{\mu }}\mathrm{s} . $ | (23) |
如此信号占空比扩展到6.8 %,去除1/4导频损失后的信息速率为14.701 5 Mbit/s。由此可见该信号信息速率可以满足一体化系统应用场景中的通信要求。
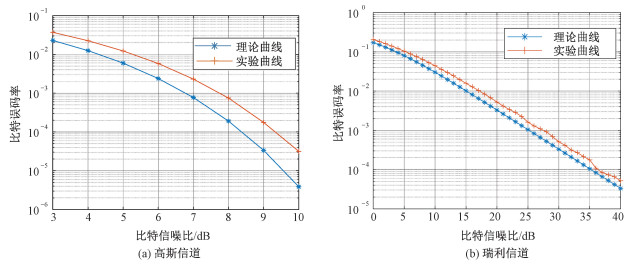
为验证信号的误码率性能,本小节仿真所提出的OFDM一体化信号在高斯信道和瑞利信道下的一体化信号误码率性能。其中瑞利信道中设计了2条路径,2条路径的信号相对幅度值为[0, -8] dB,时延差为[0, 3]/(150×106) s,仿真结果见图 7。
|
Download:
|
| 图 7 不同信道下的误码率分析图 Fig. 7 Bit error rate analysis under different channels | |
仿真结果表明,所设计的OFDM一体化信号在高斯信道误码率性能较好。当比特信噪比达到9.5 dB以上时,误码达到10-4以下,可以满足通信要求。但是在瑞利信道下,误码率性能要差很多,因为文中使用的是算法复杂度较低的迫零(zero-forcing, ZF)均衡的方法,均衡过程中没有考虑噪声的影响。可以使用最小均方误差(minimum mean squared error, MMSE)均衡方法,获得更好均衡效果;同时可以采用交织等技术改善误码率性能。总体来看,该一体化信号可以满足一体化场景下的通信性能要求。
5 结论本文主要工作总结如下:
1) 首先针对匹配滤波框架下的OFDM一体化信号处理方法导致SAR模糊函数出现高旁瓣和伪峰的问题,提出将基于CP的OFDM SAR非匹配滤波成像处理方法应用到OFDM一体化信号中,验证了该方法相较于传统的匹配滤波方法具有以下优势:①在一体化信号的成像过程中无需其他信号预编码、加权等复杂操作,就可消除通信信息对成像的影响;②同时还能有效抑制距离旁瓣,实现比传统匹配滤波方法更好的成像效果。
2) 然后针对OFDM一体化信号的高PAPR问题,提出基于DFT预编码的OFDM共享信号设计方法。该方法虽然在一定程度上影响了通信信号的抗频率选择性衰落的能力,但是能够在保证通信速率的情况下,把OFDM信号的PAPR值控制在2 dB以下,实现了峰均比可控;同时将CP段置零,降低了能源浪费,进一步提高了共享信号的适用性,从而更容易实现雷达通信一体。
3) 最后利用仿真实验验证了所提出一体化信号的成像性能和通信性能。实验证明在无噪声情况下,改进的一体化信号结合基于CP的非匹配滤波成像算法,距离向旁瓣达到-300 dB以下,可以实现距离向超低旁瓣成像;然后利用理论分析和仿真实验相结合的方法证明了该一体化信号通信速率可达到14.701 5 Mbit/s,且具有较好的误码率性能。进而证明了在非匹配滤波框架下,所提出的一体化信号可以实现通信和雷达性能的良好兼容。
| [1] |
雍萍, 王杰, 葛俊祥. 基于失配处理的OFDM雷达通信一体化共享信号旁瓣抑制技术[J]. 信号处理, 2020, 36(10): 1698-1707. Doi:10.16798/j.issn.1003-0530.2020.10.009 |
| [2] |
梁兴东, 李强, 王杰, 等. 雷达通信一体化技术研究综述[J]. 信号处理, 2020, 36(10): 1615-1627. Doi:10.16798/j.issn.1003-0530.2020.10.001 |
| [3] |
杨熙, 戎华, 王君可. 雷达-电子战-通信一体化系统雷达侦察作战效能模型研究[J]. 科技信息, 2014(13): 220-221. Doi:10.3969/j.issn.1001-9960.2014.13.155 |
| [4] |
刘永军, 廖桂生, 杨志伟. 基于OFDM的雷达通信一体化波形模糊函数分析[J]. 系统工程与电子技术, 2016, 38(9): 2008-2018. Doi:10.3969/j.issn.1001-506X.2016.09.07 |
| [5] |
曾瑞琪, 刘方正, 姜秋喜, 等. 雷达通信一体化的六种主要技术体制[J]. 现代雷达, 2019, 41(2): 10-14, 30. Doi:10.16592/j.cnki.1004-7859.2019.02.003 |
| [6] |
Moghaddasi J, Wu K. Multifunctional transceiver for future radar sensing and radio communicating data-fusion platform[J]. IEEE Access, 2016, 4: 818-838. Doi:10.1109/ACCESS.2016.2530979 |
| [7] |
Ren P, Munari A, Petrova M. Performance analysis of a time-sharing joint radar-communications network[C]//2020 International Conference on Computing, Networking and Communications (ICNC). Big Island, HI, USA. IEEE, 2020: 908-913. DOI: 10.1109/ICNC47757.2020.9049687.
|
| [8] |
Reichardt L, Sturm C, Grünhaupt F, et al. Demonstrating the use of the IEEE 802.11P car-to-car communication standard for automotive radar[C]//2012 6th European Conference on Antennas and Propagation (EUCAP). Prague, Czech Republic. IEEE, 2012: 1576-1580. DOI: 10.1109/EuCAP.2012.6206084.
|
| [9] |
李晓柏, 杨瑞娟, 程伟. 基于频率调制的多载波Chirp信号雷达通信一体化研究[J]. 电子与信息学报, 2013, 35(2): 406-412. Doi:10.3724/SP.J.1146.2012.00567 |
| [10] |
Chen X, Feng Z Y, Wei Z Q, et al. Code-division OFDM joint communication and sensing system for 6G machine-type communication[J]. IEEE Internet of Things Journal, 2021, 8(15): 12093-12105. Doi:10.1109/JIOT.2021.3060858 |
| [11] |
Liu F, Masouros C, Li A, et al. MU-MIMO communications with MIMO radar: from Co-existence to joint transmission[J]. IEEE Transactions on Wireless Communications, 2018, 17(4): 2755-2770. Doi:10.1109/TWC.2018.2803045 |
| [12] |
田团伟, 邓浩, 鲁建华, 等. 智能反射面辅助雷达通信双功能系统的多载波波形优化方法[J]. 雷达学报, 2022, 11(2): 240-254. Doi:10.12000/JR21138 |
| [13] |
伍光新, 姚元, 祁琳琳. 雷达通信波形一体化发展综述[J]. 现代雷达, 2021, 43(9): 37-45. Doi:10.16592/j.cnki.1004-7859.2021.09.007 |
| [14] |
姜孟超, 廖桂生, 杨志伟, 等. 一种NLFM-CPM雷达通信一体化信号设计[J]. 系统工程与电子技术, 2019, 41(1): 35-42. Doi:10.3969/j.issn.1001-506X.2019.01.06 |
| [15] |
周宇, 杨慧婷, 谷亚彬, 等. 基于调频率调制的雷达通信共享信号研究[J]. 电子科技大学学报, 2017, 46(6): 830-835. Doi:10.3969/j.issn.1001-0548.2017.06.006 |
| [16] |
王小江, 张贞凯. 多符号OFDM雷达通信一体化波形优化设计方法[J]. 电光与控制, 2021, 28(7): 83-87. Doi:10.3969/j.issn.1671-637X.2021.07.017 |
| [17] |
Jiang M, Qi L L, Yao Y, et al. Radar and communication integration based on OFDM signal[C]//2020 IEEE International Conference on Signal Processing, Communi-cations and Computing (ICSPCC), Macau, China. IEEE, 2020. DOI: 10.1109/ICSPCC50002.2020.9259515.
|
| [18] |
Li W L, Xiang Z, Ren P. Waveform design for dual-function radar-communication system with golay block coding[J]. IEEE Access, 2019, 7: 184053-184062. Doi:10.1109/ACCESS.2019.2960658 |
| [19] |
Levanon N. Multifrequency complementary phase-coded radar signal[J]. IEE Proceedings-Radar, Sonar and Navigation, 2000, 147(6): 276-284. Doi:10.1049/ip-rsn:20000734 |
| [20] |
Franken G E A, Nikookar H, Genderen P V. Doppler tolerance of OFDM-coded radar signals[C]//2006 European Radar Conference. Manchester, UK. IEEE, 2006: 108-111. DOI: 10.1109/EURAD.2006.280285.
|
| [21] |
周安敉. 基于OFDM的雷达通信一体化波形设计研究[D]. 石家庄: 河北科技大学, 2020.
|
| [22] |
Ma H, Sun X, Jin W X. Integrated waveform design based on spread spectrum OFDM radar communication[C]// 2019 IEEE 3rd Advanced Information Management, Communi-cates, Electronic and Automation Control Conference. Chong-qing, China. IEEE, 2020: 1258-1263. DOI: 10.1109/IMCEC46724.2019.8984147.
|
| [23] |
侯艳丽, 周安敉, 郭鑫. 基于预编码的正交频分复用雷达通信一体化信号设计[J]. 科学技术与工程, 2021, 21(2): 611-615. Doi:10.3969/j.issn.1671-1815.2021.02.028 |
| [24] |
张霄霄, 梁兴东, 王杰, 等. 融合失配处理和LMS滤波的雷达通信一体化OFDM信号距离旁瓣抑制技术[J]. 信号处理, 2021, 37(9): 1727-1738. Doi:10.16798/j.issn.1003-0530.2021.09.017 |
| [25] |
左家骏, 杨瑞娟, 程伟, 等. OFDM雷达通信共享信号距离旁瓣抑制研究[J]. 信号处理, 2020, 36(10): 1662-1667. Doi:10.16798/j.issn.1003-0530.2020.10.005 |
| [26] |
林清源, 王彦平, 洪文. 一种基于CLEAN的SAR图像旁瓣抑制方法[J]. 中国科学院研究生院学报, 2011, 28(3): 355-359. Doi:10.7523/j.issn.2095-6134.2011.3.012 |
| [27] |
张天贤, 夏香根. OFDM SAR成像方法综述[J]. 雷达学报, 2020, 9(2): 243-258. Doi:10.12000/JR19116 |
| [28] |
Zhang T X, Xia X G. OFDM synthetic aperture radar imaging with sufficient cyclic prefix[J]. IEEE Transactions on Geoscience Remote Sensing, 2014, 53(1): 394-404. Doi:10.1109/TGRS.2014.2322813 |
| [29] |
李占亚, 张光荣, 陈晓辉, 等. 同时含有限幅失真和量化失真的OFDM系统的联合优化[J]. 中国科学院大学学报, 2014, 31(2): 249-256. Doi:10.7523/jssn.2095-6134.2014.02.016 |
| [30] |
Armstrong J. Peak-to-average power reduction for OFDM by repeated clipping and frequency domain filtering[J]. Electronics Letters, 2002, 38(5): 246-247. Doi:10.1049/el:20020175 |
| [31] |
Wang Y, Ge J H, Wang L H, et al. Reduction of PAPR of OFDM signals using nonlinear companding transform[J]. Wireless Personal Communications, 2013, 71(1): 383-397. Doi:10.1007/s11277-012-0820-2 |
| [32] |
Bäuml R W, Fischer R F H, Huber J B. Reducing the peak-to-average power ratio of multicarrier modulation by selected mapping[J]. Electronics Letters, 1996, 32(22): 2056-2057. Doi:10.1049/el:19961384 |
| [33] |
Hasan M M. VLM precoded SLM technique for PAPR reduction in OFDM systems[J]. Wireless Personal Communi-cations, 2013, 73(3): 791-801. Doi:10.1007/s11277-013-1217-6 |
| [34] |
Hu S C, Wan S J, Yang M, et al. An improved SLM algorithm for OFDMA system with implicit side information[J]. Journal of Signal Processing Systems, 2022, 94(8): 837-846. Doi:10.1007/s11265-022-01750-x |
| [35] |
Goel A, Gupta S. Side information embedding scheme for PTS based PAPR reduction in OFDM systems[J]. Alexandria Engineering Journal, 2022, 61(12): 11765-11777. Doi:10.1016/j.aej.2022.05.021 |
| [36] |
Chen C Y, Wang C H, Chao C C. Complementary sets and reed-muller codes for peak-to-average power ratio reduction in OFDM[M]//Applied Algebra, Algebraic Algorithms and Error-Correcting Codes. Berlin, Heidelberg: Springer Berlin Heidelberg, 2006: 317-327. DOI: 10.1007/11617983_31.
|
| [37] |
Sengupta S, Lande B K. An approach to PAPR reduction in OFDM using Goppa codes[J]. Procedia Computer Science, 2020, 167: 1268-1280. Doi:10.1016/j.procs.2020.03.443 |
| [38] |
Garmatyuk D. Cross-range SAR reconstruction with multicarrier OFDM signals[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(5): 808-812. Doi:10.1109/LGRS.2011.2182176 |
| [39] |
Garmatyuk D, Brenneman M. Adaptive multicarrier OFDM SAR signal processing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(10): 3780-3790. Doi:10.1109/TGRS.2011.2165546 |
 2024, Vol. 41
2024, Vol. 41 


