近年来,合成孔径雷达[1-4] (synthetic aperture radar, SAR)已经广泛应用于各个领域,如灾害检测、军事侦察、环境监测等。与传统的光学和红外传感器相比,SAR具有全天时、全天候、高分辨率等特点。SAR的基本原理是通过平台的运动来合成大孔径天线,从而在方位向上得到高分辨率的图像。在传统的SAR成像模式中,天线的侧面指向几乎是垂直于雷达平台的前进方向的。但是在一些特殊的SAR系统中,为了提前获取更前方的图像信息,天线需要从垂直位置向前偏移数十度的指向,如弹载SAR[5-6]。相比传统的侧向SAR,斜视SAR可以通过调整斜视角度对同一个区域进行多次观察,从而获取高分辨率目标图像。
虽然斜视SAR具有很多优点,同时它也带来许多新的问题。高斜视角引起的不同信号特性,带来新的复杂性和困难。许多成像算法被提出用于解决这些问题,如距离多普勒(range Doppler,RD)算法[7-8]、omega-K算法[9]、后向投影算法[10-11]和chirp scaling(CS)算法[12-14]等。在这些算法中,CS算法是最出名和重要的算法之一。该算法的聚焦能力强且实现简单,其基本思路是基于scaling原理,通过相位相乘,实现对信号的尺度变换,在距离多普勒域中将信号与变标方程相乘实现补余距离徙动校正,之后二维频域的相位相乘完成剩余的距离徙动校正。由于距离徙动矫正并不需要任何复杂的插值运算,因此在成像算法中广泛应用。
随着数字信号处理技术的发展,一些时频的分析工具[15-17]被引入雷达信号处理领域。分数阶傅里叶变换(fractional Fourier transform,FRFT)[18]由于其固有的chirp信号结构,在雷达信号处理中收到越来越多的关注[19-21]。2006年,Amein和Soraghan[22]发表了一篇基于分数阶傅里叶变换的改进CS成像算法的文章,该算法利用FRFT代替传统的FFT并推导了封闭表达式,但该算法只是用FRFT代替FFT,导致算法计算的复杂性。2010年,Clemente和Soraghan[23]提出基于FRFT的RD算法,但文献只是对正侧视SAR情况进行分析,未对斜视SAR的距离徙动矫正给出理论依据。2012年,李昕和邢丽坤[24]提出利用FRFT的距离多普勒域成像算法。该算法将传统算法中的匹配滤波利用FRFT,得到的结果图像旁瓣更低。但该算法仍需要复杂的插值运算。
针对以上问题,本文提出基于FRFT的改进CS成像算法,从而实现高分辨率的SAR图像。该算法从斜视SAR回波信号模型上进行理论推导,由于采用的是CS成像算法,因此避免了复杂的插值运算。仿真和实验结果表明该算法成像分辨率更高,验证了算法的有效性。
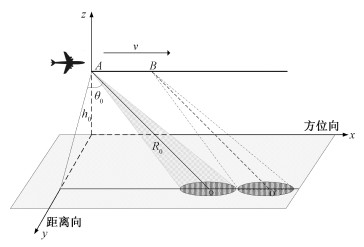
1 回波信号模型和FRFT 1.1 回波信号模型首先建立斜视SAR雷达信号的回波模型,斜视SAR成像几何模型如图 1所示,雷达的速度用v表示,平台的运行轨迹假设以理想的直线飞行情况沿AB方向前进,平台距离地面的高度用h0表示。深色区域为雷达发射脉冲信号的照射区域,称为波束覆盖区域。目标与雷达平台的最短距离为R0,距离向与雷达照射方向所成的夹角称为斜视角,用θr表示。
|
Download:
|
| 图 1 斜视SAR成像几何模型 Fig. 1 Geometric model of strabismus SAR imaging | |
接着推导回波模型,首先在距离向上,雷达发射线性调频脉冲信号为
| $ s_p(\tau)=w_\tau(\tau) \cos \left(2 \pi f_0 \tau+\pi K_r \tau^2\right), $ | (1) |
其中:τ表示为距离时间,f0为发射信号的中心频率,Kτ为线性调频信号的调频率,wτ(τ)=rect
| $ \begin{aligned} s_0(\tau, \eta)= & A_0 w_\tau\left(\tau-\frac{2 R(\eta)}{c}\right) w_a\left(\eta-\eta_c\right)\cdot \\ & \exp \left[{{\mathrm{j}}} \pi K_r\left(\tau-\frac{2 R(\eta)}{c}\right)^2\right]\cdot \\ & \exp \left(-{{\mathrm{j}}} \frac{4 \pi f_0 R(\eta)}{c}\right), \end{aligned} $ | (2) |
其中:η为方位时间;A0为回波信号的幅度,大小和反射系数相关;c为光速;wa为方位向脉冲包络;ηc为方位中心时间。R(η)为距离方程,在斜视SAR下,距离方程为
| $ \begin{aligned} R(\eta) & =\sqrt{R_0^2+v^2 \eta^2-2 R_0 v \eta \sin \theta_r} \\ & \approx R_0-v \eta \sin \theta_r+\frac{\cos ^2 \theta_r}{2 R_0} v^2 \eta^2 \\ & \approx \sqrt{R_0^2+\left(v \eta \cos \theta_r\right)^2}-v \eta \sin \theta_r. \end{aligned} $ | (3) |
为便于分析,对距离方程进行泰勒展开,在传统的正侧视SAR中,总距离徙动主要由二次分量组成。然而,在斜视合成孔径雷达中,线性分量通常远大于二次分量。因此,在本文中,针对斜视SAR,只保留二阶以下的展开项,忽略高阶项影响,并且会在之后的方位向聚焦上利用图像加权熵对成像精度进行提高。
1.2 FRFTFRFT是傅里叶变换的推广形式,它可以认为是信号的chirp分解或者是信号在时频的平面上旋转一个角度α,而传统傅里叶变换相当于信号在时频平面旋转90°。给定任意一个信号x(t),其角度为α的FRFT可以表示为
| $ X_\alpha(u)=\int\limits_{-\infty}^{\infty} x(t) K_\alpha(t, u) {{\mathrm{d}}} t, $ | (4) |
其中,FRFT的变换核Kα(t, u)为
| $ K_\alpha(t, u)= \begin{cases}\sqrt{\frac{1-{{\mathrm{j}}} \cos \alpha}{2 \pi}} {{\text{e}}^{\text{j}\frac{{{t}^{2}}+{{u}^{2}}}{2}\cot \alpha -\text{j}ut\csc \alpha }}, & \alpha \neq k \pi, \\ \delta(t-u), & \alpha=2 k \pi, \\ \delta(t+u), & \alpha=2 k \pi+\pi.\end{cases} $ | (5) |
FRFT相比于传统的傅里叶变换能够更好地处理chirp信号,这是因为chirp信号在时频平面内呈现为一条直线,而FRFT是在一组相互正交的chirp基上展开的,其变换核的核心是调频率为cotα的chirp信号,正如单频正弦信号经过傅里叶变换就会变成单频基上的冲激函数一样,一旦chirp信号与某组基的调频率吻合,那么该信号在分数阶傅里叶变换之后必然也会成为一个冲激函数,而在其他的基上为0。这说明chirp信号在分数阶傅里叶变换领域上具有很好的聚焦性,同时它还是一个线性变换。这也相当于对chirp信号进行了匹配滤波。
根据文献[25],可以得到采样chirp信号的最优FRFT旋转角的阶次popt
| $ p_{{\mathrm{opt}}}=\frac{2}{\pi} \alpha_{{\mathrm{opt}}}=-\frac{2}{\pi} \tan ^{-1}\left(\frac{f_s^2 / N}{2 a}\right), $ | (6) |
其中:fs表示采样频率,N表示信号采样数量,a表示chirp信号的调频率。
2 改进CS成像算法为获得高质量的SAR图像,提出一种新的改进CS成像算法,主要分为4个步骤:首先进行线性距离徙动校正(linear rang walk correction,LRWC),去除回波信号中交叉耦合的线性分量,之后在距离多普勒域进行chirp scaling操作,消除距离偏移的空间变异性,接着分别进行距离向和方位向的FRFT对信号进行聚焦操作。
2.1 LRWCLRWC操作是通过乘以一个线性相位因子实现的,以此消除回波信号中交叉耦合的线性分量。首先对式(2)回波信号进行距离向α=π/2的FRFT或传统傅里叶变换,之后乘以线性因子H1(fτ, η)
| $ H_1\left(f_\tau, \eta\right)=\exp \left(-{{\mathrm{j}}} \frac{4 \pi\left(f_0+f_\tau\right)}{c} v \eta \sin \theta_r\right), $ | (7) |
其中fτ表示距离频率。两式相乘之后对该信号进行距离向α=-π/2的FRFT,得到校正之后的信号s1(τ, η)
| $ \begin{aligned} s_1(\tau, \eta)= & A_0 w_\tau\left(\tau-\frac{2 R_1\left(\eta, R_0\right)}{c}\right) w_a\left(\eta-\eta_c\right) \cdot \\ & \exp \left(-\frac{{{\mathrm{j}}} 4 \pi f_0 R_1\left(\eta, R_0\right)}{c}\right) \cdot \\ & \exp \left[{{\mathrm{j}}} \pi K_r\left(\tau-\frac{2 R_1\left(\eta, R_0\right)}{c}\right)^2\right], \end{aligned} $ | (8) |
其中:R1(η, R0)表示对斜视SAR进行LRWC后新的距离方程,
观察式(8),可以发现,通过将v转换成vcosθr,LRWC相当于将斜视SAR信号转换成正侧视SAR信号,通过该操作使得后续的成像处理过程更加容易。
2.2 Chirp scaling下一步操作首先将信号计算方位向α=π/2的FRFT,将信号变换到距离信号多普勒域,进行chirp scaling,将不同距离处的距离徙动转变成和参考距离处一致,即补余距离徙动校正。之后计算距离向α=π/2的FRFT,变换到二维频域,在该域完成一致距离徙动校正以及除掉残余相位。
将s1(τ, η)进行方位向α=π/2的FRFT得到信号Srd1(τ, fη)
| $ \begin{aligned} S_{{\mathrm{rd1}}}\left(\tau, f_\eta\right)= & A_0 w_\tau\left(\tau-\frac{2 R_1\left(f_\eta, R_0\right)}{c}\right)\cdot \\ & W_a\left(f_\eta-f_{\eta_c}\right) \cdot \\ & \exp \left[{{\mathrm{j}}} \pi K_m\left(\tau-\frac{2 R_1\left(f_\eta, R_0\right)}{c}\right)^2\right] \cdot\\ & \exp \left(-\frac{{{\mathrm{j}}} 4 \pi f_0 R_0}{c} \sqrt{1-\left(\frac{f_\eta}{f_{\eta_c}}\right)^2}\right), \end{aligned} $ | (9) |
其中:fη表示方位频率;Wa表示方位频率包络;方位向中心频率
| $ R_1\left(f_\eta, R_0\right)=\frac{R_0}{\sqrt{1-\left(\frac{f_\eta}{f_{\eta_c}}\right)^2}}=\frac{R_0}{D\left(f_\eta\right)} . $ | (10) |
令
| $ \begin{aligned} & H_2\left(\tau, f_\eta\right)=\exp \left\{{{\mathrm{j}}} \pi K_m\left[\frac{D\left(f_{\eta_{\text {ref }}}\right)}{D\left(f_\eta\right)}-1\right] .\right. \\ & \left.\left(\tau-\frac{2 R_1\left(f_\eta, R_{\text {ref }}\right)}{{\mathrm{c}}}\right)^2\right\}, \end{aligned} $ | (11) |
其中:fηref为参考方位频率,Rref为参考距离。将变标方程与式(9)相乘,之后变换到二维频域,得到S2df(fτ, fη)
| $ \begin{aligned} & S_{2 {{\mathrm{df}}}}\left(f_\tau, f_\eta\right)=A_1 W_r\left(f_\tau\right) W_a\left(f_\eta-f_{\eta_c}\right) \cdot \\ & \exp \left(-{{\mathrm{j}}} \frac{\pi D\left(f_\eta\right)}{K_m D\left(f_{\eta_{\text {ref }}}\right)} f_\tau^2\right) \cdot \exp \left(-{{\mathrm{j}}} \frac{4 \pi R_0}{c D\left(f_{\eta_{\text {ref }}}\right)} f_\tau\right) \cdot \\ & \exp \left\{-{{\mathrm{j}}} \frac{4 \pi}{{{\mathrm{c}}}}\left[\frac{1}{D\left(f_\eta\right)}-\frac{1}{D\left(f_{\eta_{\text {ref }}}\right)}\right] R_{\text {ref }} f_\tau\right\} \cdot \\ & \exp \left\{{{\mathrm{j}}} \frac{4 \pi K_m}{c^2}\left[1-\frac{D\left(f_\eta\right)}{D\left(f_{\eta_{\text {ref }}}\right)}\right]\left[\frac{R_0}{D\left(f_\eta\right)}-\frac{R_{\text {ref }}}{D\left(f_\eta\right)}\right]^2\right\} \cdot \\ & \exp \left(-{{\mathrm{j}}} \frac{4 \pi R_0 f_0 D\left(f_\eta\right)}{c}\right), \end{aligned} $ | (12) |
其中Wr为距离频率。第1和第2个指数项分别为距离调制和方位调制,第3个指数项为目标点位置,第4和第5个指数项分别为一个附加残余相位和一致距离徙动一个附加残余相位。通过乘以共轭因子,补偿一致距离徙动和残余相位,完成所有的距离徙动校正操作。之后回到距离多普勒域
| $ \begin{aligned} & S_{{{\mathrm{rd}}} 2}\left(\tau, f_\eta\right)=A_2 w_r\left(\tau-\frac{2 R_1\left(f_\eta, R_0\right)}{c}\right) W_a\left(f_\eta-f_{\eta c}\right) \cdot \\ & \quad \exp \left[{{\mathrm{j}}} \pi K_m \frac{D\left(f_{\eta_{\text {ref }}}\right)}{D\left(f_\eta\right)} \cdot\left(\tau-2 R_0 / c D\left(f_{\eta_{\text {ref }}}\right)\right)^2\right] \cdot \\ & \quad \exp \left\{-{{\mathrm{j}}} \frac{4 \pi R_0 f_0 D\left(f_\eta\right)}{c}\right\} . \end{aligned} $ | (13) |
在传统的CS成像算法中,下一步操作时利用匹配滤波完成脉冲压缩,本节将直接利用FRFT完成该步骤。首先利用FRFT完成距离向压缩,对式(13)进行距离向FRFT,得到Srd3(τ, fη)
| $ S_{{{\mathrm{rd}}} 3}\left(u_\tau, f_\eta\right)=\int S_{{{\mathrm{rd}}} 2}\left(\tau, f_\eta\right) K_{\alpha_{{{\mathrm{opt}}}}}\left(\tau, u_\tau\right) {{\mathrm{d}}} \tau, $ | (14) |
其中:uτ为距离分数频域变量,αopt为距离向最优旋转角。根据式(7)可以得到距离向最优旋转阶次为
| $ p_{\text {opt }}=-\frac{2}{\pi} \arctan \left(\frac{D\left(f_\eta\right) f_s^2}{K_m D\left(f_{\eta_{\text {ref }}}\right) N}\right) . $ | (15) |
将式(15)代入式(14)中
| $ \begin{aligned} S_{\text {rd3 }}\left(u_\tau f_\eta\right)= & W_a\left(f_\eta-f_{\eta c}\right) \exp \left(-{\mathrm{j}} \frac{4 \pi R_0 f_0 D\left(f_\eta\right)}{c}\right) \cdot \\ & {\rm{sinc}}\left[\frac{T_\tau}{2} \csc \alpha_{\text {opt }}\left(u_\tau-t_0 \cos \alpha_{\text {opt }}\right)\right] . \\ & \exp \left[{\mathrm{j}} \frac{\cot \alpha_{\text {opt }}}{2}\left(u_\tau^2-t_0^2\right)\right] . \end{aligned} $ | (16) |
Srd3(uτ, fη)即为经过距离压缩后的回波信号,最后一个指数项为FRFT之后的残余相位。为避免出现散焦,通过乘以相位因子去除掉该项,最终得到距离向FRFT之后的信号
| $ \begin{aligned} S_{{\mathrm{rd}} 3}\left(u_\tau, f_\eta\right)= & W_a\left(f_\eta-f_{\eta c}\right) \cdot \\ & {\rm{sinc}}\left[\frac{T_\tau}{2} \csc \alpha_{\text {opt }}\left(u_\tau-t_0 \cos \alpha_{\text {opt }}\right)\right] \cdot\\ & \exp \left(-{\mathrm{j}} \frac{4 \pi R_0 f_0 D\left(f_\eta\right)}{c}\right). \end{aligned} $ | (17) |
观察式(17)可以发现,第2个指数函数为双曲线函数,需要经过近似变换成二次函数才会成为chirp信号。且在变换之后,不同距离单元处的多普勒调频率是不相同的。同时由于缓变的运动误差为双曲线型,其影响方位向调频率,所以直接使用标准的匹配滤波器会造成失配。针对上述问题,为了精确地获得方位向的FRFT最优旋转角,提高方位向的聚焦效果,本节将利用加权最小熵的聚焦算法,通过加权熵建立代价函数,并采用迭代方法完成最优旋转角的搜索,进而获得高分辨SAR图像。
信号进行方位向FRFT后可以表示为
| $ s_4\left(u_\tau, u_\eta\right)=\int S_{{{\mathrm{rd}}} 3}\left(u_\tau, f_\eta\right) K_\beta\left(f_\eta, u_\eta\right) {{\mathrm{d}}} \tau, $ | (18) |
其中β表示方位向FRFT旋转角。图像熵可以对信号的聚焦程度进行衡量,当图像散焦时,图像熵会比较大,反之,当图像聚焦良好时,图像熵会比较小。但如果利用最小熵算法作为代价函数求解参数时,每个方位向数据具有相同的参数值,而通常情况下,不同方位向数据的信号信杂比是不同的,为此应根据信杂比的强弱来确定权值的大小。文献[26]给出信杂比的计算方法,但该方法是为聚束SAR设计的,为此首先进行转化:
| $ \begin{aligned} s s\left(u_\eta, R\right)= & {\mathbf{F}}^{-1}\left\{{\mathbf{F}}\left\{s_4\left(u_\eta, R\right)\right\} {\mathbf{F}}\left\{s_{\text {ref }}\left(u_\eta, R\right)\right\}\right\} \cdot \\ & \left(s_{\text {ref }}\left(u_\eta, R\right)\right)^*, \end{aligned} $ | (19) |
其中:ss(uη, R)表示参考距离为R处的方位信号,F表示傅里叶变换,F-1表示傅里叶逆变换,参考信号sref(uη, R)为
| $ \begin{gathered} s_{\text {ref }}\left(u_\eta, R\right)= \\ \exp \left(-{{\mathrm{j}}} \frac{4 \pi R f_0}{c} \cdot\left(1-\sqrt{1-\left(\frac{v \eta}{\sqrt{R+(v \eta)^2}}\right)^2}\right)\right). \end{gathered} $ | (20) |
信杂比的计算公式为
| $ \begin{aligned} & {{\mathrm{SCR}}}=\frac{d}{4\left(2 c^2-d\right)-4 c \sqrt{4 c^2-3 d}}, \\ & c={{\mathrm{E}}}\left[\left|s s\left(u_\eta, R_0\right)\right|\right], d={{\mathrm{E}}}\left[\left|s s\left(u_\eta, R_0\right)\right|^2\right]. \end{aligned} $ | (21) |
根据信杂比的强弱获取合适的权值wm,令p(uτ, uη)=s4(uτ, uη)s4*(uτ, uη),建立加权最小熵的代价函数为
| $ I(\beta)= -\sum_{m=0}^{M-1} \sum_{n=0}^{N-1} w_m \frac{p\left(u_\tau, u_\eta\right)}{S} \ln \left(\frac{p\left(u_\tau, u_\eta\right)}{S}\right) \\ = -\frac{1}{S} \sum_{m=0}^{M-1} \sum_{n=0}^{N-1} w_m p\left(u_\tau, u_\eta\right) \ln \left(p\left(u_\tau, u_\eta\right)\right)+ \\ \frac{\ln S}{S} \sum_{m=0}^{M-1} \sum_{n=0}^{N-1} w_m p\left(u_\tau, u_\eta\right) \\ = -\frac{1}{S} \sum_{m=0}^{M-1} \sum_{n=0}^{N-1} w_m p\left(u_\tau, u_\eta\right) \ln \left(p\left(u_\tau, u_\eta\right)\right)+C, $ | (22) |
其中: M和N分别表示图像矩阵的行数和列数;
| $ \frac{\partial I(\beta)}{\partial \beta}=-\frac{1}{S} \sum_{m=0}^{M-1} \sum_{n=0}^{N-1} w_m \cdot \\ \quad\left(\frac{\partial p\left(u_\tau, u_\eta\right)}{\partial \beta} \ln \left(p\left(u_\tau, u_\eta\right)\right)+\frac{\partial p\left(u_\tau, u_\eta\right)}{\partial \beta}\right) . $ | (23) |
观察式(23)可以发现,一阶导数涉及p(uτ, uη)的求导。在文献[27]中,Candan提出离散FRFT的变换核 Fβ可以写为
| $ {\mathbf{F}}^\beta=\sum_{n=0}^{N-1} \exp (-{{\mathrm{j}}} n \beta) H_{n, 1}(u) H_{n, 1}(t), $ | (24) |
其中Hn, 1(x)表示阶数为n的Hermite多项式,通过式(24)将变换核进行特征值分解,即
| $ \begin{gathered} {\mathbf{F}}^\beta={\boldsymbol{U}} \cdot {\boldsymbol{D}} \cdot {\boldsymbol{U}}^{{{\mathrm{H}}}}, \\ {\boldsymbol{D}}=\operatorname{diag}\left\{{{\mathrm{e}}}^0, {{\mathrm{e}}}^{-{{\mathrm{j}}} \beta}, {{\mathrm{e}}}^{-{{\mathrm{j}}} 2 \beta}, \cdots, {{\mathrm{e}}}^{-{{\mathrm{j}}}(N-1) \beta}\right\}, \end{gathered} $ | (25) |
其中:U表示Fβ的特征向量矩阵,而D是特征值矩阵。如果用 X表示Srd3(uτ, fη)的矩阵形式,根据特征值分解可以得到p(uτ, uη)的矩阵表示 P
| $ {\boldsymbol{P}}=\left({\boldsymbol{U}} {\boldsymbol{D}} {\boldsymbol{U}}^{{\mathrm{H}}} {\boldsymbol{X}}\right) \odot\left({\boldsymbol{U}} {\boldsymbol{D}} {\boldsymbol{U}}^{{\mathrm{H}}} {\boldsymbol{X}}\right)^*, $ | (26) |
其中⊙表示Hardmard积。根据式(26)写出P的一阶导数,进而计算出代价函数的导数值,P的一阶导数为
| $ \begin{aligned} \frac{\partial {\boldsymbol{P}}}{\partial \beta}= & \left({\boldsymbol{U}} {\boldsymbol{\varLambda}} {\boldsymbol{D}} {\boldsymbol{U}}^{{\mathrm{H}}} {\boldsymbol{X}}\right) \odot\left({\boldsymbol{U}} {\boldsymbol{D}} {\boldsymbol{U}}^{{\mathrm{H}}} {\boldsymbol{X}}\right)^*+ \\ & \left({\boldsymbol{U}} {\boldsymbol{D}} {\boldsymbol{U}}^{{\mathrm{H}}} {\boldsymbol{X}}\right) \odot\left({\boldsymbol{U}} {\boldsymbol{\varLambda}} {\boldsymbol{D}} {\boldsymbol{U}}^{{\mathrm{H}}} {\boldsymbol{X}}\right)^*, \end{aligned} $ | (27) |
其中:Λ =diag{0, -j, -j2, …, -j(N-1)}。基于得到的梯度值,利用动量法进行迭代计算,不断更新参数值,直到收敛。在0°~180°旋转角内,目标函数在全局内存在唯一最小值,因此对其应用动量法进行迭代计算,其结果必然收敛到最小值。动量法的更新规则如下所示
| $ \begin{gathered} m_k=\gamma m_{k-1}-\mu \frac{\partial {\boldsymbol{P}}}{\partial \beta}, \\ \beta_k=\beta_{k-1}-m_k, \end{gathered} $ | (28) |
其中:mk为第k次的速度更新;γ为动量参数,是一个小于1的数;μ为学习率,一般取0.5或者0.9。通过迭代计算方位向FRFT最优旋转阶次,之后进行方位向FRFT,得到s4(uτ, uη)
| $ \begin{aligned} s_4\left(u_\tau, u_\eta\right)= & \int S_{\text {rd3 }}\left(u_\tau, f_\eta\right) K_{\beta_{\text {opt }}}\left(f_\eta, u_\eta\right) {\mathrm{d}} f_\eta \\ = & \exp \left\{-{\mathrm{j}} \frac{4 \pi R_0 f_0}{c}\right\} {\rm{sinc}}\left[\frac{T_\eta}{2} u_\tau \csc \beta_{\text {opt }}\right] . \\ & {\rm{sinc}}\left[\frac{T_\tau}{2} \csc \alpha_{\text {opt }}\left(u_\tau-t_0 \cos \alpha_{\text {opt }}\right)\right] . \\ & \exp \left[{\mathrm{j}} \frac{\cot \beta_{\text {opt }}}{2} u_\eta^2\right] . \end{aligned} $ | (29) |
之后,方位向FRFT产生的残余相位利用和距离向一样的方法去除,便可得到最终的SAR图像,图像的表达式为
| $ \begin{aligned} s_4\left(u_\tau, u_\eta\right)= & \exp \left\{-{\mathrm{j}} \frac{4 \pi R_0 f_0}{c}\right\} \operatorname{sinc}\left[\frac{T_\eta}{2} u_\tau \csc \beta_{\text {opt }}\right] . \\ & \operatorname{sinc}\left[\frac{T_\tau}{2} \csc \alpha_{\text {opt }}\left(u_\tau-t_0 \cos \alpha_{\text {opt }}\right)\right]. \end{aligned} $ | (30) |
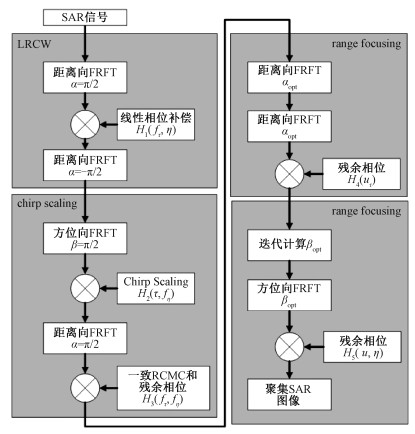
根据上述推导,整体改进CS成像算法的流程如图 2所示。
|
Download:
|
| 图 2 改进CS成像算法流程图 Fig. 2 Flow chart of improved CS imaging algorithm | |
为验证改进CS成像算法的性能,本节分别利用仿真数据以及实测SAR数据对算法进行测试,观察实验结果。并利用峰值旁瓣比、积分旁瓣比以及图像分辨率等评价标准与传统CS成像算法进行对比分析。
3.1 仿真实验结果首先进行仿真实验的测试,根据相关参数设计雷达回波信号,仿真相关参数设置如表 1所示。
|
|
表 1 点目标仿真参数 Table 1 Point target simulation parameters |
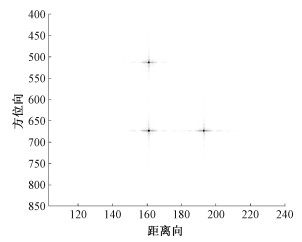
仿真实验中,给定3个点目标的回波数据,其中:点目标1和点目标2的距离向相同,方位向相差120 m;点目标2和点目标3方位向相同,距离向相差50 m。利用本文提出的算法对回波数据进行成像,成像结果如图 3所示。
|
Download:
|
| 图 3 基于改进算法的仿真成像结果 Fig. 3 Simulation imaging results based on the improved algorithm | |
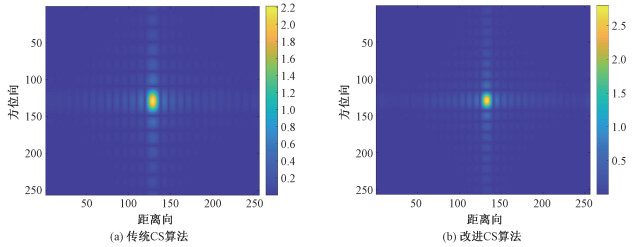
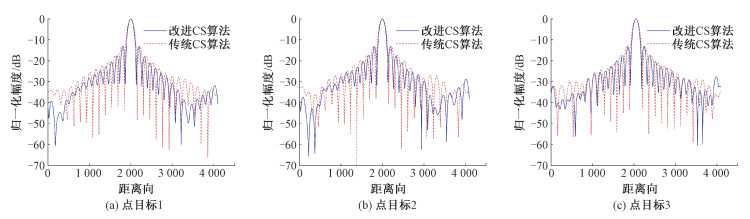
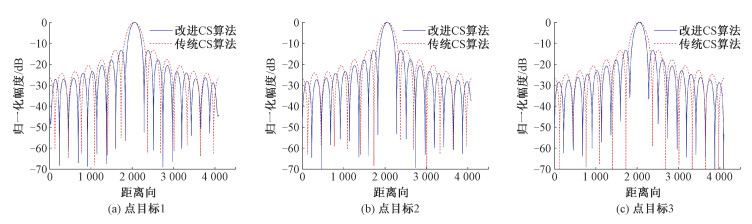
为验证该算法的性能,将该算法的成像结果与传统CS成像算法进行对比,将2个算法中的3个点目标依次取出进行升采样,观察得到的图像。之后对点目标进行切片操作,对比观察同一个点目标下的距离向和方位向的性能指标。图 4为2种算法的对比成像结果,为便于阅读,这里只简单展示点目标1的对比结果。图 5展示2种算法的3个点目标距离向切片结果对比图,图 6展示2种算法的3个点目标方位向切片结果对比图。
|
Download:
|
| 图 4 2种算法对点目标1的仿真结果 Fig. 4 Simulation results of two algorithms on point target 1 | |
|
Download:
|
| 图 5 距离向切片结果对比 Fig. 5 Comparison of distance slice results | |
|
Download:
|
| 图 6 方位向切片结果对比 Fig. 6 Comparison of azimuth section results | |
通过观察同一个目标在2种算法下的成像结果,可以发现,2种算法都能够对距离的空间变异性进行补偿。在距离向和方位向聚集上,改进算法中的聚焦效果要明显优于传统算法。并且改进算法中无论是距离向或是方位向的旁瓣都能够更好地被抑制。其主要原因是分数阶傅里叶变换可以看成是时频轴的旋转,分数阶傅里叶变换之后chirp信号具有更宽的带宽,带宽越大分辨率越高。即使带宽很窄,在持续时间足够长的情况下,分辨率的提升也很大。
为进一步研究改进CS算法的性能,利用峰值旁瓣比(peak side lobe ratio,PSLR)、积分旁瓣比(integration side lobe ratio,ISLR)以及脉冲分辨率(又称冲激响应宽度,impulse response width,IRW)等相关评判标准对上面的仿真结果进行量化标准的检测。PSLR、ISLR越小说明旁瓣越小,IRW越小,说明主瓣越窄,图像的分辨率越高,图像的聚焦效果越好。其结果如表 2所示。不难发现,改进算法的PSLR、ISLR和IRW相关指标均小于传统算法,聚焦效果更好,成像质量要优于传统算法。
|
|
表 2 成像质量评判结果 Table 2 Evaluation results of imaging quality |
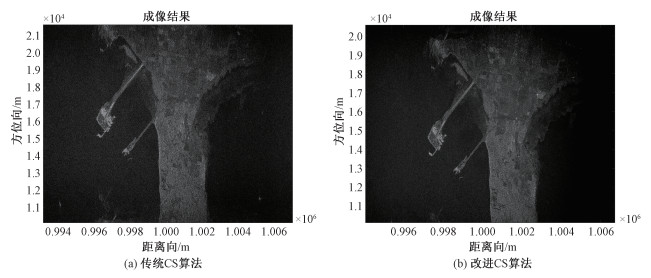
在仿真实验之后,利用加拿大温哥华RADARSAT-1实测数据集对本文提出的算法做进一步测试。分别利用传统算法和改进算法对该数据集进行成像测试,图 7展示2个算法成像结果对比图。根据成像图像,可以看出改进算法的成像效果更好,图像更清晰,聚焦效果优势明显。
|
Download:
|
| 图 7 2种算法成像图对比 Fig. 7 Comparison of imaging images of the two algorithms | |
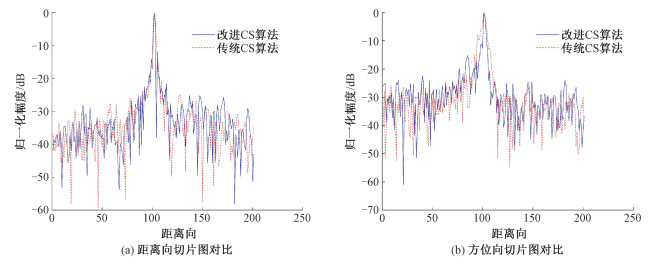
为进一步验证图像的成像质量,在图像中选取散射点最强的地方,对其进行切片操作,获取距离向方位向的切片数据,对数据进行归一化处理,其结果对比如图 8所示。从图 8可以看出,改进CS算法的成像效果无论是在距离向还是在方位向,主瓣宽度都更窄,旁瓣更低,能够在2个方向上都提升图像的聚焦效果,改善图像的聚焦质量。
|
Download:
|
| 图 8 最强散射点切片图对比 Fig. 8 Section comparison of the strongest scattering points | |
本文提出基于分数阶傅里叶变换的改进CS成像算法,从理论公式对算法进行逐步推导,针对方位向聚焦问题,利用加权最小熵算法进行改进。由仿真结果可以看出,通过与传统成像算法进行对比,本文提出的算法明显改进了成像质量,主瓣宽度变窄,提升了成像的聚焦性,并且算法的收敛性良好。
| [1] |
Jiang Z H, Huang-Fu K, Wan J W. A chirp transform algorithm for processing squint mode FMCW SAR data[J]. IEEE Geoscience and Remote Sensing Letters, 2007, 4(3): 377-381. Doi:10.1109/LGRS.2007.895689 |
| [2] |
Xiong T, Xing M D, Xia X G, et al. New applications of Omega-K algorithm for SAR data processing using effective wavelength at high squint[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(5): 3156-3169. Doi:10.1109/TGRS.2012.2213342 |
| [3] |
Khwaja A S, Ferro-Famil L, Pottier E. Efficient stripmap SAR raw data generation taking into account sensor trajectory deviations[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(4): 794-798. Doi:10.1109/LGRS.2011.2111411 |
| [4] |
Vandewal M, Speck R, Süß H. Efficient and precise processing for squinted spotlight SAR through a modified stolt mapping[J]. EURASIP Journal on Advances in Signal Processing, 2006, 2007: 059704. Doi:10.1155/2007/59704 |
| [5] |
Chen S, Zhao H C, Zhang S N, et al. An extended nonlinear chirp scaling algorithm for missile borne SAR imaging[J]. Signal Processing, 2014, 99: 58-68. Doi:10.1016/j.sigpro.2013.12.017 |
| [6] |
周松, 周鹏, 李亚超, 等. 弹载SAR下降段成像算法研究[J]. 西安电子科技大学学报, 2011, 38(3): 90-98. |
| [7] |
葛立敏, 李宏, 刘肖. 改进的斜视机载合成孔径雷达RD成像算法[J]. 计算机仿真, 2009, 26(11): 14-16, 64. |
| [8] |
Yeo T S, Tan N L, Zhang C B, et al. A new subaperture approach to high squint SAR processing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(5): 954-968. Doi:10.1109/36.921413 |
| [9] |
Tang S Y, Zhang L R, Guo P, et al. An Omega-K algorithm for highly squinted missile-borne SAR with constant acceleration[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(9): 1569-1573. Doi:10.1109/LGRS.2014.2301718 |
| [10] |
叶晓明, 张国峰, 胡晓光, 等. 近前视弹载SAR的改进后向投影成像算法[J]. 北京航空航天大学学报, 2015, 41(3): 492-501. Doi:10.13700/j.bh.1001-5965.2014.0223 |
| [11] |
Desai M D, Jenkins W K. Convolution backprojection image reconstruction for spotlight mode synthetic aperture radar[J]. IEEE Transactions on Image Processing, 1992, 1(4): 505-517. Doi:10.1109/83.199920 |
| [12] |
Moreira A, Huang Y H. Airborne SAR processing of highly squinted data using a chirp scaling approach with integrated motion compensation[J]. IEEE Transactions on Geoscience and Remote Sensing, 1994, 32(5): 1029-1040. Doi:10.1109/36.312891 |
| [13] |
Moreira A, Mittermayer J, Scheiber R. Extended chirp scaling algorithm for air-and spaceborne SAR data processing in stripmap and ScanSAR imaging modes[J]. IEEE Transactions on Geoscience and Remote Sensing, 1996, 34(5): 1123-1136. Doi:10.1109/36.536528 |
| [14] |
Davidson G W, Cumming I G, Ito M R. A chirp scaling approach for processing squint mode SAR data[J]. IEEE Transactions on Aerospace and Electronic Systems, 1996, 32(1): 121-133. Doi:10.1109/7.481254 |
| [15] |
Chen V C, Ling H. Time-frequency transforms for radar imaging and signal analysis[M]. Boston, MA: Artech House, 2002.
|
| [16] |
Namias V. The fractional order Fourier transform and its application to quantum mechanics[J]. IMA Journal of Applied Mathematics, 1980, 25(3): 241-265. Doi:10.1093/imamat/25.3.241 |
| [17] |
Sejdić E, Djurović I, Stanković L. Fractional Fourier transform as a signal processing tool: an overview of recent developments[J]. Signal Processing, 2011, 91(6): 1351-1369. Doi:10.1016/j.sigpro.2010.10.008 |
| [18] |
陶然, 邓兵, 王越. 分数阶傅里叶变换及其应用[M]. 北京: 清华大学出版社, 2009.
|
| [19] |
陈勇, 赵惠昌, 陈思, 等. 基于分数阶傅里叶变换的弹载SAR成像算法[J]. 物理学报, 2014, 63(11): 118403. Doi:10.7498/aps.63.118403 |
| [20] |
Pepin M, Hayat M M. Fast synthetic aperture radar imaging with a streamlined 2D fractional Fourier transform[C]//SPIE Defense, Security, and Sensing. Proc SPIE 8051, Algorithms for Synthetic Aperture Radar Imagery XVIII, Orlando, Florida, USA. 2011, 8051: 9-20. DOI: 10.1117/12.883862.
|
| [21] |
Amein A S, Soraghan J J. Azimuth fractional transformation of the fractional chirp scaling algorithm (FrCSA)[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(10): 2871-2879. Doi:10.1109/TGRS.2006.877757 |
| [22] |
Amein A S, Soraghan J J. A new chirp scaling algorithm based on the fractional Fourier transform[J]. IEEE Signal Processing Letters, 2005, 12(10): 705-708. Doi:10.1109/LSP.2005.855547 |
| [23] |
Clemente C, Soraghan J J. Fractional RDA and enhanced FrCSA for SAR imaging[C]//Sensor Signal Processing for Defence (SSPD 2010). London, UK. IET, 2010. DOI: 10.1049/ic.2010.0243.
|
| [24] |
李昕, 邢丽坤. 斜视SAR分数阶距离多普勒成像算法[J]. 计算机工程, 2012, 38(13): 247-250. Doi:10.3969/j.issn.1000-3428.2012.13.074 |
| [25] |
Capus C, Brown K. Short-time fractional Fourier methods for the time-frequency representation of chirp signals[J]. The Journal of the Acoustical Society of America, 2003, 113(6): 3253-3263. Doi:10.1121/1.1570434 |
| [26] |
Ye W, Yeo T S, Bao Z. Weighted least-squares estimation of phase errors for SAR/ISAR autofocus[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(5): 2487-2494. Doi:10.1109/36.789644 |
| [27] |
Candan C, Kutay M A, Ozaktas H M. The discrete fractional Fourier transform[J]. IEEE Transactions on Signal Processing, 2000, 48(5): 1329-1337. Doi:10.1109/78.839980 |
 2024, Vol. 41
2024, Vol. 41 


