2. 中国科学院大学电子电气与通信工程学院, 北京 100049
2. School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 100049, China
随着时代的发展,社会各行各业对多光谱遥感数据的需求趋于多元化,对近地面多光谱影像的获取方式、波段配准及数据定量化等方面提出了新的要求[1]。当前市面上多光谱相机种类众多,如多镜头多波段式、光路分光式和阵列滤光片式等,但是每种相机都存在一定的不足[2]。其中,多镜头相机近距离成像时成像视差会造成波段配准问题,不同波段所用的镜头和探测器参数差异会带来辐射畸变问题;光路分光式多光谱相机像素数少、体积重量大、探测器成本高、波段数少;阵列滤光片式多光谱相机数据处理复杂、数据的可用性较差。滤光片转轮式的多光谱相机成像方式中镜头和探测器位置相对固定,每个波段成像光路一致,地物目标和外界成像条件对多波段数据的影响一致,波段配准简单,数据的可用性较强, 但由于波段成像时刻的差异,转动部件会带来一致性偏差,需要针对性处理。中国科学院遥感与数字地球研究所和国家航天局共同研制机载单CCD 4波段航空遥感相机[3],美国Ocean Insight公司推出SpectroCamTM 6~8波段多光谱相机。多光谱遥感影像的预处理分为几何校正、辐射校正、大气校正等。通常情况下,在进行几何校正之前先进行影像的辐射校正,即对图像数据中依附于辐射亮度的各种失真进行校正。目前国内外学者对转轮式的多光谱相机及其数据辐射校正的研究相对较少,本文基于自主研发的近地面滤光片转轮式多光谱相机,对所获数据的预处理方法进行研究,主要是分析转轮成像方式对多波段影像的一致性、重复性等方面的影响,为进一步建立该滤光片转轮式多光谱相机获取的遥感信息与观测地表的目标参量之间的关系和遥感的定量化应用奠定基础,同时丰富轻量化的多光谱相机类型,助力多光谱遥感的发展。
1 滤光片转轮式多光谱相机本文介绍一款自研滤光片转轮式的多光谱相机,如图 1所示,该相机采用单面阵COMS探测器多光谱通道共享感光光路,通过分时切换实现单镜头多波段成像。此外,曝光时间可调,滤光片可以根据相机使用场景定制。研究选取6个广泛应用于农业、林业、资源、生态和环境保护等领域的波段定制滤光片,分别是450、555、660、705、750和830 nm,相机的其他指标参数如表 1所示。

|
Download:
|
| 图 1 滤光片转轮式多光谱相机 Fig. 1 Filter wheel type multispectral camera | |
|
|
表 1 待测相机指标参数 Table 1 Parameters of the camera to be tested |
辐射校正分为相对辐射校正和绝对辐射校正,本文通过实验室辐射定标方法对传感器本身的光学系统特征以及光电变换系统的灵敏度特征进行校正[4]。基于待测相机获取的训练数据,对影像整体的辐射不均匀性、暗噪声、条带噪声、坏线等进行修正,确定相机各波段输入的辐射能量和输出响应之间的相关关系,即增益和偏置系数,将其DN值(digital number)转换为波谱辐射亮度,建立系统入瞳辐射亮度值L(λ)与系统输出数字灰度DN值之间的定量关系,反演出图像信息代表的辐射特性。
2.1 相对辐射校正方法相对辐射校正又称为去条带校正或均匀化校正,其方法是使用相对辐射校正系数作用于原始图像,消除由于传感器或电荷耦合器件的探元响应不一致引起的辐射不均匀效应[5-6]。响应不均匀性问题受多种因素影响,如探测器的材料属性以及生产工艺等,从而给待测相机获取的数据引入了固定噪声,形式上表现为暗电流和光电响应的不均匀性[7]。目前常用的相对辐射定标方法有基于实验室定标的方法、基于统计学的匹配法、空间滤波法等[8]。定标法采用传感器的定标系数进行影像校正,可对探测器的响应差异进行调整,适用于各类辐射不均匀的校正,且相较于统计法定标精度较高,因此采用基于实验室定标的相对辐射校正方法对待测相机进行校正。在不改变获取影像整体DN值的前提下,引入辐射校正模型,修正探测器单元响应不均匀以及相机光学元件各部分光学透过率不同引起的辐射不均匀性问题[9-10]。
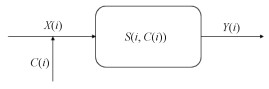
基于实验室定标的相对辐射校正数学模型如图 2所示。其中,X(i)代表原始遥感影像,i表示像素编号,C(i)代表训练数据,S(i,C(i))代表传感器定标模型,Y(i)代表校正后遥感影像,则有Y(i)=X(i)S(i,C(i))。
|
Download:
|
| 图 2 相对辐射校正数学模型 Fig. 2 Schematic of calibration-based methods | |
辐射定标的数学表达式可表示为
| $ \begin{gathered} {\rm{DN}}(i, j, \lambda)=\left[{\rm{DN}}(i, j, \lambda)_{\text {测量值 }}-\right. \\ \left.{\rm{DN}}(i, j, \lambda)_{\text {疃樔声 }}\right] \times A(i, j, \lambda) . \end{gathered} $ | (1) |
式中:DN(i, j, λ)测量值、DN(i, j, λ)暗噪声、A(i, j, λ)分别是中心波长为λ的光谱通道中探测器第i行、第j列像元对应的实际测量值、暗噪声和非均匀性校正系数;DN(i, j, λ)是去除暗噪声并经过均匀性校正后的灰度值。
2.2 绝对辐射定标方法随着各行业对遥感数据的需求逐渐强烈,定量遥感已经成为遥感科学发展的趋势。绝对辐射定标是将待测相机获取影像的DN值转换为入瞳处的辐射亮度的过程,用来克服双向反射分布函数效应、太阳高度角、云的阴影、相机的增益及其曝光时间的设置等因素对探测器响应的影响,建立如上探测器输出量和入瞳处辐射能量之间的数量关系是进行遥感定量化的基础[11]。从成像过程来看,入瞳光谱辐射能量经镜头传播到达成像传感器,利用光电转换原理测量入射能量的强弱,输出不同量化等级的数值并记录在影像文件中。数值的大小与入射光谱能量有关,表征地物对电磁波谱的反射能力。在定量遥感分析中,为准确求得地物的反射率,需要对影像做绝对辐射定标,将像元值转换为入瞳处的波谱辐射亮度,为遥感的定量化反演提供数据基础[12]。
多光谱遥感数据的绝对辐射校正一般采用基于统计学的经验线性方法,首先认为每个像素的DN值与传感器探测到的辐射能量具有直接的线性关系,对于待测相机的每个光谱通道,可以建立相应通道的DN值与辐射亮度之间的关系模型
| $ L(i, j, \lambda)={\boldsymbol{a}} \cdot {\mathrm{DN}}(i, j, \lambda)+{\boldsymbol{b}}. $ | (2) |
其中:L(i, j, λ)为DN(i, j, λ)输出值对应的光谱辐亮度;a、b为辐射定标系数矩阵。辐射定标就是确定每个探测像元的a、b值,在实际观测时测得DN(i, j, λ)即可计算出L(i, j, λ)。
3 实验与分析实验在中国科学院空天信息创新研究院定标实验室进行,环境温度为20~25 ℃,湿度在60 % 以下,除实验所用积分球外无其他光源。辐射定标系统主要由积分球、待测相机和光谱辐射计组成。积分球出自Labsphere公司,如图 3所示,其漫反射特性的均匀性好、稳定性强,辐亮度角度均匀性优于98 %,输出亮度级别可以连续调节。利用该辐射定标系统获取的训练数据进行最优积分时间的确定、暗噪声的校正、相对辐射校正和绝对辐射校正。

|
Download:
|
| 图 3 实验场景 Fig. 3 The experimental scene | |
滤光片转轮式多光谱相机主要特点是旋转滤光片分时获取不同波段的影像,在不同积分时间、不同转速、数据一致性方面会对多光谱影像的辐射特性带来影响。本实验首先检验工作方式对多光谱影像的一致性差异。将相机的积分时间分别设定为5、10、15、20 ms,在同一光源下进行连续的数据采集,选取滤光片转动至第1、3、5周获取的数据进行重复性和线性度分析,结果如表 2所示。该结果表明待测相机没有因为滤光片的转动带来明显的辐射畸变,相机的工作状态稳定且数据的重复性较好,因此滤光片转动带来的影响可在后续的相对辐射校正中一并去除。
|
|
表 2 重复性和线性度对比 Table 2 Comparison experiment of repeatability and linearity |
探测器积分时间就是曝光时间,相当于普通胶片相机的快门从打开到关闭的时间,积分时间越长,进入相机到探测器表面的光线越多,图像越亮。但是当积分时间达到一定长度时,图像会出现部分或全白,此时认为图像过饱和。反之,积分时间越短,图像越暗。因此在实验室中需要确定待测相机各个波段在不同环境亮度下合适的积分时间,为相机在投入使用时能够合理地选择和设置积分时间提供参考。
在定标实验室中利用积分球和待测相机进行数据采集,通过设置不同的电流值调整积分球的亮度。本实验选择8个辐射亮度,分别为最大亮度的30 %、40 %、50 %、60 %、70 %、80 %、90 % 和100 %。积分时间选择5、8、10、12、15和20 ms。在如上亮度和积分时间下获取大量训练数据,建立不同波长和不同积分时间下影像灰度值和辐射亮度之间的相关关系,根据拟合优度R2大小判断直线和观测值的拟合效果。R2的最大值为1,越接近1表示数据的拟合效果越好。根据不同波段获取影像灰度值和辐射亮度的线性拟合效果,判断待测相机各波段合适的积分时间。
经线性拟合选出的各波段较为合适的积分时间及其拟合优度R2如表 3所示。实验结果显示750 nm波段图像整体较亮,应选择较小的积分时间,防止图像过饱和;450和705 nm波段图像整体较暗,应选择相对较大的积分时间,分别为30和15 ms,防止影像的亮度较低;其他波段的积分时间均选择在12 ms左右,保持影像亮度表现适中。
|
|
表 3 待测相机各波段的积分时间 Table 3 The integral time of each band of the camera to be tested |
滤光片转轮式多光谱相机使用的是COMS图像传感器,受传感器电子元件、电路结构、材料属性、工作环境等因素的影响,会产生一些固定噪声,表现为暗噪声,影响数据的应用。暗噪声是指在进行光谱测量时环境中的杂光,实际上是实验室测量系统内部的噪声。它影响待测相机获取的原始数据精度,因此在构建相对辐射校正模型之前需要先进行暗噪声的校正。一般通过去除暗背景的方式消除实际光谱测量中的暗噪声。
去除暗背景进行暗噪声校正前,需要提前开启相机使其进入工作状态,待相机的自身温度和工作状态稳定后,切断所有光源使待测相机处于黑暗环境中,根据3.1节的实验结果设置待测相机各波段的积分时间,再进行数据采集。获取影像的DN值即为电子的离散特性导致的暗噪声,在进行相对辐射校正时需要逐像素地用测量值减去暗噪声值。
3.3 相对辐射校正相对辐射校正本质上是对相机探测器的响应不均匀性问题进行纠正。通常来说,同一个探测器的光电响应特性应该是一定的,因此相对辐射校正的策略是选择一个单色光源释放均匀分布的光信号,利用探测器探元的光电响应不均匀性建立校正模型纠正整幅图像的光信号[13]。
在定标实验室中利用积分球和待测相机进行数据采集,首先将相机各通道的积分时间按照表 3进行调整,然后通过设置不同的电流值调整积分球亮度至最大亮度的30 %、40 %、50 %、60 %、70 % 和80 %,在保证数据具有一定灰度差异的同时防止出现过饱和的现象。获取的训练数据显示,该相机的探测器单元响应具有一定的不均匀性,导致获取的影像存在一定程度的辐射不均现象[14-15]。如图 4(a)所示,在均匀光源照射下待测相机获取的影像左右两侧边缘上没有明显的“黑边”问题,但是四周存在一定程度的暗角,有明显的边缘减光现象。

|
Download:
|
| 图 4 待测相机训练数据示例 Fig. 4 Example of training data for the camera under test | |
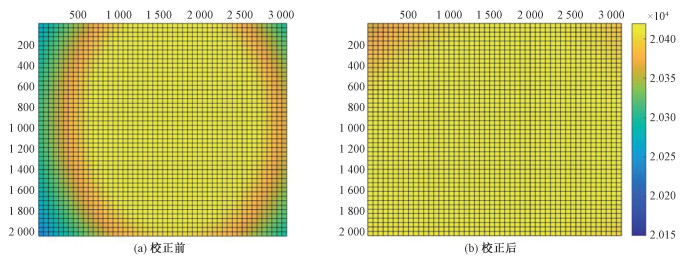
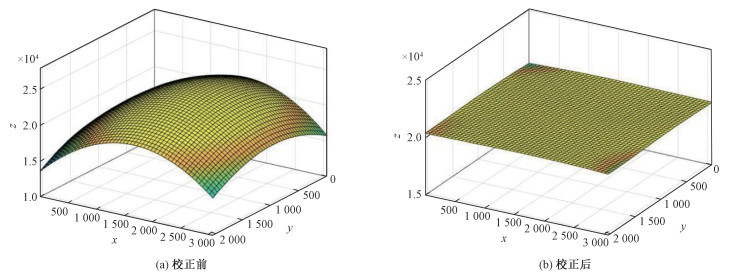
多级亮度定标法是利用灰度直方图统计其中一个波段单幅训练图像中占比最大的灰度值作为该图像的标准值,求取第i行、第j列的DN值与标准值的比值,得到该像元的非均匀性校正系数A,进一步构建该波段的相对辐射校正模型。利用不同亮度等级下获取的训练数据,进一步修正各波段校正模型的精度,使模型在实际应用中达到更好的效果。图 5是根据待测相机获取的训练数据提取其坐标和对应灰度值绘制的伪彩色图像,突出表现校正前后图像各部分灰度差异,显示效果更加直观。图 6是三维空间中的图像模型,x、y轴表示每一个像元对应的行、列号,z轴表示像素的DN值。校正前的模型呈中间高四周低的灰度畸变状态,校正后的模型灰度分布均匀,而校正结果符合预期。
|
Download:
|
| 图 5 示例数据的灰度分布伪彩色图 Fig. 5 Pseudo-color graph of grayscale distribution of sample data | |
|
Download:
|
| 图 6 示例数据的三维模型 Fig. 6 Image 3D model of the sample data | |
使用统计学方法,将待测相机各波段图像校正前后的灰度统计进行比较,得到的结果符合预期目标。选择部分实验数据证明相对辐射校正模型的校正效果:1)选择70 % 亮度下6个波段校正前后的统计结果进行比较,如表 4所示。校正前的DN值平均偏差最小为8.333 %,最大为13.395 %;校正后的像素平均偏差最小为1.414 %,最大为1.928 %。校正后DN值的方差比校正前下降2个数量级,校正的精度可以达到97 %,校正误差可以控制在3 % 左右;2)选择555 nm波段下6个不同亮度校正前后的统计结果进行比较,如表 4所示。校正前的DN值平均偏差最小为8.544 %,最大为9.394 %;校正后的像素平均偏差最小为1.039 %,最大为1.728 %。校正的精度可以达到98 %,校正误差可以控制在2 % 左右。可见实验得到的相对辐射校正模型对不同亮度下待测相机各波段的数据适用性较强。该模型可以在不改变图像整体灰度值的前提下改善相机探测器的响应不均匀性问题,且其精度满足绝对辐射校正的需求。
|
|
表 4 灰度统计结果 Table 4 Gray statistical results |
利用已经获得的相对辐射校正模型对待测相机的室外实拍数据进行校正,选取830 nm的影像进行彩色变换,以提高图像显示的视觉效果。校正前后的影像如图 7所示,从整体上看校正前后图像的灰度值没有发生太大变化,但校正后图像4个角的亮度明显增强。这表明实验得到的相对辐射校正模型可以校正探测器响应不均匀所造成的边缘减光效应,且校正结果符合预期。

|
Download:
|
| 图 7 待测相机实拍数据相对辐射校正 Fig. 7 Relative radiometric correction of real shot data from the camera to be tested | |
绝对辐射定标是在相对辐射定标的基础上进行的,它将待测相机获取的DN值转换为绝对辐射亮度值, 为后续的遥感数据应用提供数据基础。相对辐射校正模型对各像元的DN值进行调整[16-17],会改变整张影像的灰度值,影响绝对辐射定标结果的精度。因此,在绝对辐射校正过程中,需要确定相对辐射校正后像元值间和辐射亮度之间的转换关系,得到绝对辐射定标系数。这样可以缩小反演出的辐射亮度与实际情况间的差异,为后续的定量化应用提供满足精度要求的基础数据。
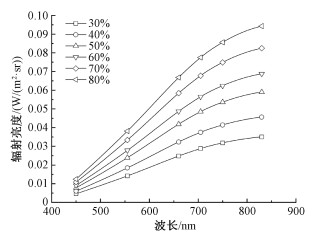
进行绝对辐射定标需要获取积分球的标准辐射亮度数据和待测相机的训练数据:1)图 8为定标实验室积分球的标准辐射亮度曲线,记录最大亮度30 %、40 %、50 %、60 %、70 % 和80 % 时对应的标准辐射亮度值,如表 5所示;2)使用3.3节中经过相对辐射校正的训练数据,获取不同亮度下各波段获取影像的灰度直方图,统计校正后影像中占比最大的DN值并将其记为标准值。最后通过线性回归得到校正后影像标准值和标准辐射亮度的转换关系,其增益和偏置如表 6所示。
|
Download:
|
| 图 8 积分球不同亮度下的辐射亮度曲线 Fig. 8 Radiation brightness curve of integrating sphere under different brightness | |
|
|
表 5 不同亮度下的辐射亮度实测数据 Table 5 Standard value of radiant brightness |
|
|
表 6 绝对辐射定标系数 Table 6 Absolute radiative calibration coefficient |
随着社会对多元化的遥感数据和定量化的遥感反演需求的不断增长,涌现出许多不同类型的多光谱相机。针对普通多光谱相机存在的如大多配备复杂的分光设备、体积大灵活性低、数据预处理复杂等问题,介绍了一款自研轻小型滤光片转轮式多光谱相机。在相机投入使用前需要进行辐射校正,改正镜头传输及传感器响应产生的辐射畸变。设计了不同亮度、不同积分时间下的数据采集和处理实验,确定该款新相机各波段最优的积分时间范围。使用多级亮度定标法构建相对辐射校正模型对影像整体的辐射不均性、暗噪声等进行修正,并利用经验线性法将影像中记录的灰度值转换为入瞳处的波谱辐射亮度。辐射校正和定标结果显示,所选校正系数对不同成像条件的多光谱影像具有高度的稳定性和可靠性,为进一步实现滤光片转轮式多光谱数据的遥感解译、反演地表目标的参量和各类定量化应用奠定了基础。当前的辐射校正方法多为半手工方式,操作复杂。如何提高辐射校正的自动化程度,是未来辐射校正需要解决的问题之一。
| [1] |
李德仁. 摄影测量与遥感的现状及发展趋势[J]. 武汉测绘科技大学学报, 2000, 25(1): 1-6. Doi:10.13203/j.whugis2000.01.001 |
| [2] |
冯晨阳, 梁玉斌, 张虎, 等. 无人机多光谱影像的几何与辐射校正[J]. 天津师范大学学报(自然科学版), 2021, 41(2): 65-73. Doi:10.19638/j.issn1671-1114.20210211 |
| [3] |
刁静静, 袁占良, 陈继平, 等. 无人机载单CCD四波段多光谱相机的几何预处理[J]. 测绘通报, 2012(S1): 231-232, 248. |
| [4] |
张文君, 张智文, 陈生奇, 等. 基于LCTF的多光谱成像系统辐射定标[J]. 光学与光电技术, 2016, 14(4): 38-43. |
| [5] |
Dinguirard M, Slater P N. Calibration of space-multispactral imaging sensors: a review[J]. Remote Sensing of Environment, 1999, 68(3): 194-205. Doi:10.1016/S0034-4257(98)00111-4 |
| [6] |
Chen J S, Lin H, Shao Y, et al. Oblique striping removal in remote sensing imagery based on wavelet transform[J]. International Journal of Remote Sensing, 2006, 27(8): 1717-1723. Doi:10.1080/01431160500185516 |
| [7] |
陈迎娟, 张之江, 张智强. CCD像素响应不均匀性的校正方法[J]. 光学精密工程, 2004, 12(2): 216-220. |
| [8] |
段依妮, 张立福, 晏磊, 等. 遥感影像相对辐射校正方法及适用性研究[J]. 遥感学报, 2014, 18(3): 597-617. Doi:10.11834/jrs.20143204 |
| [9] |
孙长麟, 汪红强. 遥感影像相对辐射校正算法设计与实现[J]. 信息与电脑(理论版), 2021, 33(17): 77-80. Doi:10.3969/j.issn.1003-9767.2021.17.023 |
| [10] |
张兵, 张浩, 陈正超, 等. 一种基于图像统计量的相对辐射纠正算法[J]. 遥感学报, 2006, 10(5): 630-635. |
| [11] |
孙刚, 黄文江, 陈鹏飞, 等. 轻小型无人机多光谱遥感技术应用进展[J]. 农业机械学报, 2018, 49(3): 1-17. Doi:10.6041/j.issn.1000-1298.2018.03.001 |
| [12] |
黄莉婷, 焦伟利, 龙腾飞, 等. 基于正则化IR-MAD的GF-1影像辐射归一化[J]. 遥感信息, 2020, 35(3): 99-109. Doi:10.3969/j.issn.1000-3177.2020.03.014 |
| [13] |
许和鱼, 张黎明, 李鑫, 等. 基于太阳漫反射板线阵CCD相对辐射定标方法研究[J]. 光学学报, 2020, 40(6): 179-187. Doi:10.3788/AOS202040.0628002 |
| [14] |
李慧芳, 沈焕锋, 张良培, 等. 一种基于变分Retinex的遥感影像不均匀性校正方法[J]. 测绘学报, 2010, 39(6): 585-591, 598. |
| [15] |
潘志强, 顾行发, 刘国栋, 等. 基于探元直方图匹配的CBERS-01星CCD数据相对辐射校正方法[J]. 武汉大学学报(信息科学版), 2005, 30(10): 925-927. |
| [16] |
陈劲松, 邵芸, 朱博勤. 中分辨率遥感图像条带噪声的去除[J]. 遥感学报, 2004, 8(3): 227-233. |
| [17] |
Acito N, Diani M, Corsini G. Subspace-based striping noise reduction in hyperspectral images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(4): 1325-1342. Doi:10.1109/TGRS.2010.2081370 |
 2024, Vol. 41
2024, Vol. 41 


