2. 中国科学院大学,北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
现代合成孔径雷达(synthetic aperture radar,SAR)距离分辨率由雷达激励信号带宽决定。要实现高分辨率的雷达图像,产生宽带雷达信号是必不可少的前提条件。国内及国际上对高分辨率成像技术的研究一直是成像雷达领域重要的技术发展方向之一,分辨率已经从最初的几十m提高到cm量级[1-3]。为实现系统的分辨率要求,雷达激励信号产生系统在实现超宽带雷达信号的同时,其产生信号还必须具有优良的频谱纯度以及近似理想的幅相特性,这就对系统实现提出了越来越高的要求。
目前模拟正交调制是雷达激励信号产生系统中最常用也是最核心的技术手段[4-5],正交调制实现了对基带IQ形成的复信号进行频谱搬移的过程。对于基带每一路的I/Q实信号带宽为B,经过正交调制后的信号带宽为2B,这样在上变频的同时带宽加倍,能够充分利用信号带宽,对ADC的采样率要求降低。在正交调制的基础上,可以根据系统需求再次通过混频对频谱二次搬移或者通过倍频对信号频谱进行扩展,最后激励信号推动末级功放形成大功率雷达发射信号。上述整个雷达发射通道在具体实施过程中,数字基带信号源、模拟正交调制、滤波、放大、混频/倍频、功放等环节带来的幅相误差失真等都会影响最终产生的雷达发射信号质量,影响脉冲压缩结果,最终影响成像质量。尤其是其中的模拟正交调制环节,由于内部实际模拟电路非对称特性引起IQ两路的幅相不平衡,这会造成正交调制输出信号出现杂散信号。杂散信号分为载频泄漏和镜频干扰两部分,如果这两部分杂散不能够被有效抑制,再进入后端的混频/倍频及功放后会由于多阶交调形成更为复杂的杂散分量,从而严重恶化最终信号的谱质[6]。那么在上述情况下,如果仅在雷达的接收解调阶段进行IQ幅相不平衡的补偿校正工作,并不能有效改善收发系统的整体特性,这也是在雷达系统的发射端进行正交调制幅相不平衡预失真校正的意义所在。
对于模拟正交调制形成的载频泄漏杂散分量,通过设计偏置电路对输入I/Q信号的直流偏置进行调整,可以对本振(local oscillator, LO)泄漏进行有效对消,去除载频泄漏分量。而镜频干扰的抑制要靠改善IQ两路信号的幅相不平衡来实现。对于IQ幅相不平衡的失真补偿技术,多用于数字通信系统[7-9]。由于数字通信系统信号瞬时带宽窄,通常只有几十MHz,内部正交调制单元可以仅针对载频附近的幅相特性进行补偿, 补偿方法主要有基于神经网络迭代或者基于多项式等算法。但对于宽带SAR系统,发射通道的正交调制的幅相失真则是工作频率的函数,随着频率的变化而变化,补偿难度较大。针对宽带系统,现有的失真校正方法中,其中一类是通过引入反馈支路来实时监测输出信号[10-11],反馈信号用于估计IQ支路的失配并进行数字预失真调整,这类方法反馈环路及算法的复杂度会影响系统的实时性;另外一类算法是通过拟合和统计直接估计或跟踪输出IQ支路的失真补偿函数[12-13],系统复杂度虽然降低,但对算法提出了较高的要求,且多数情况下,都是利用仿真数据验证算法有效性,并没有利用实际系统和实际信号进行校正工作, 无法评估真实的补偿效果。文献[14]提出一种自适应预失真和跟踪方案,直接估计补偿函数,最终的验证工作也是通过仿真证明的。文献[15]采用实际系统对补偿方法进行验证,系统瞬时带宽为MHz量级,补偿后的最大相位误差12°。
本文提出一种正交调制幅相不平衡预失真校正方法,该方法通过误差分析与建模,提取包含幅相不平衡在内的所有系统幅相误差,并将系统误差映射到数字基带信号输出的IQ支路上,通过数字预失真来补偿整个发射系统带来的失真杂散问题。本方法主要适用于SAR和ISAR宽带雷达系统。通过对实际系统以及信号进行测试分析,采用预失真技术,在不需要增加额外硬件支持的情况下,具有超宽带(最大瞬时带宽GHz量级,信号相对带宽>20%)幅相失真补偿的能力,补偿后镜频抑制度大于39 dB,激励信号相位误差小于5.7°(0.1 rad)。而且本方法建立的误差模型有效涵盖了雷达发射通道内部所有产生误差的通路,具有对称性和完备性,更能够反映真实的系统误差。通过实际系统的搭建和试验,也充分证明经过校正后,发射激励信号谱质改善明显。
1 误差分析与建模首先需要指出,对于实际雷达发射系统,会存在非线性电路部分,比如发射通道中的混频或者倍频单元电路。在实际硬件电路搭建过程中,需要采用具有如下3个特点的非线性元件:1)具有平坦的宽带幅频特性;2)具有宽带相位线性度;3)具有一定的输入输出动态范围。在上述条件下,可以采用线性系统理论进行系统的误差分析和建模。
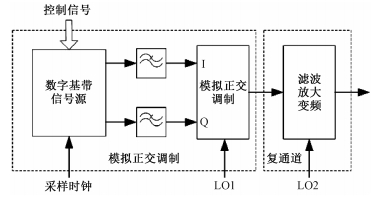
根据线性系统理论可知,一个具有幅度和相位失真的系统可以等效为一个理想无失真系统与一个误差网络级联。所以,整体思路是首先要建立系统误差模型,再设法去除失真网络的影响,来实现对整个系统的误差校正。本文所论述的SAR激励信号产生系统原理图如图 1所示。
|
Download:
|
| 图 1 正交调制发射通道原理图 Fig. 1 Principle of I/Q modulated in transmission channel | |
由图 1可知,可以将整个发射系统分为模拟正交调制与复通道2个部分,下面针对2个部分的误差模型进行分析与建模。
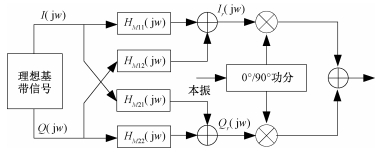
1.1 模拟正交调制误差模型对于实际的模拟正交调制部分,其内部I、Q支路不可避免会存在幅相不一致,同时本振端的90°功分也并非理想。另外,数字基带信号源产生的I、Q信号以及后端的模拟低通滤波器也会存在一定的幅相不对称性。所有这些因素终可归结为模拟正交调制的幅相不平衡,而且在宽带雷达系统中,这些幅相不平衡是频率的缓变函数,随频率的不同而不同。在进行系统误差建模时,可将系统看成是非理想失真模型和理想正交调制系统级联。将所有的幅相不平衡归结到IQ两支路之上以及IQ支路之间,建立具体误差模型如图 2所示。
|
Download:
|
| 图 2 模拟正交调制误差模型 Fig. 2 Error model of analog quadrature modulation | |
根据误差模型有如下关系式
| $ \boldsymbol{H}_{M}(\mathrm{j} w)=\left[\begin{array}{ll} H_{M 11}(\mathrm{j} w) & H_{M 12}(\mathrm{j} w) \\ H_{M 21}(\mathrm{j} w) & H_{M 22}(\mathrm{j} w) \end{array}\right], \\ $ | (1) |
| $ I_{r}(\mathrm{j} w)=I(\mathrm{j} w) H_{M 11}(\mathrm{j} w)+Q(\mathrm{j} w) H_{M 12}(\mathrm{j} w), $ | (2) |
| $ Q_{r}(\mathrm{j} w)=Q(\mathrm{j} w) H_{M 22}(\mathrm{j} w)+I(\mathrm{j} w) H_{M 21}(\mathrm{j} w). $ | (3) |
其中: I(jw)和Q(jw)为理想线性调频信号(linear frequency modulation, LFM)基带信号频谱,Ir(jw)和Qr(jw)是经过系统的非理想特性后包含所有幅相不平衡性的实际基带信号频谱。系统传输函数HM11(jw)、HM12(jw)、HM21(jw)、HM22(jw)包含模拟正交调制系统中所有的幅相不平衡特性。
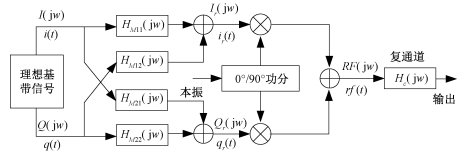
1.2 复通道误差模型在实际的SAR雷达发射链路中,模拟正交调制后的信道部分为复通道部分。设Hc(jw)为整个发射复通道的系统传输函数,系统误差模型如图 3所示。
|
Download:
|
| 图 3 发射系统误差模型 Fig. 3 Error model of transmitting channel | |
根据正交调制的数学模型
| $ rf(t)=i_{r}(t) \cos \left(w_{0} t\right)+q_{r}(t) \sin \left(w_{0} t\right), $ | (4) |
对其进行傅里叶变换后得到
| $ \begin{aligned} R F(\mathrm{j} w)= & {\mathsf{π}}\left[I_{r}\left(\mathrm{j} w+\mathrm{j} w_{0}\right)+I_{r}\left(\mathrm{j} w-\mathrm{j} w_{0}\right)\right]+ \\ & \mathrm{j} {\mathsf{π}}\left[Q_{r}\left(\mathrm{j} w+\mathrm{j} w_{0}\right)-Q_{r}\left(\mathrm{j} w-\mathrm{j} w_{0}\right)\right]. \end{aligned} $ | (5) |
其中:ir(t)和qr(t)为正交调制误差模型中具有不平衡误差的同相正交分量; Ir(jw)和Qr(jw)为对应的信号频谱; w0为正交调制本振角频率。
对于复通道的传输函数Hc(jw)可以将其进行正交分解,即将其看成是两路基带信号hi(t)和hq(t)通过理想正交调制得到的[15]。即
| $ h_{c}(t)=h_{i}(t) \cos \left(w_{0} t\right)+h_{q}(t) \sin \left(w_{0} t\right). $ | (6) |
则有
| $ \begin{align*} H_{c}(\mathrm{j} w)= & {\mathsf{π}}\left[H_{i}\left(\mathrm{j} w+\mathrm{j} w_{0}\right)+H_{i}\left(\mathrm{j} w-\mathrm{j} w_{0}\right)\right]+ \\ & \mathrm{j} {\mathsf{π}}\left[H_{q}\left(\mathrm{j} w+\mathrm{j} w_{0}\right)-H_{q}\left(\mathrm{j} w-\mathrm{j} w_{0}\right)\right]. \end{align*} $ | (7) |
其中:Hi(jw)和Hq(jw)为复系统传函正交分解后的基带信号频谱。
那么,总系统输出为
| $ Y(\mathrm{j} w)=R F(\mathrm{j} w) H_{c}(\mathrm{j} w). $ | (8) |
将式(5)和式(7)代入式(8)后进行整理,如下
| $ \begin{align*} Y(\mathrm{j} w)=&{\mathsf{π}}^{2}\left[I_{r}\left(\mathrm{j} w+\mathrm{j} w_{0}\right) H_{i}\left(\mathrm{j} w+\mathrm{j} w_{0}\right)+I_{r}\left(\mathrm{j} w-\mathrm{j} w_{0}\right) H_{i}\left(\mathrm{j} w-\mathrm{j} w_{0}\right)-\right.\\ & \left.Q_{r}\left(\mathrm{j} w+\mathrm{j} w_{0}\right) H_{q}\left(\mathrm{j} w+\mathrm{j} w_{0}\right)-Q_{r}\left(\mathrm{j} w-\mathrm{j} w_{0}\right) H_{q}\left(\mathrm{j} w-\mathrm{j} w_{0}\right)\right]+ \\ & \mathrm{j} {\mathsf{π}}^{2}\left[I_{r}\left(\mathrm{j} w+\mathrm{j} w_{0}\right) H_{q}\left(\mathrm{j} w+\mathrm{j} w_{0}\right)-I_{r}\left(\mathrm{j} w-\mathrm{j} w_{0}\right) H_{q}\left(\mathrm{j} w-\mathrm{j} w_{0}\right)+\right. \\ & \left.Q_{r}\left(\mathrm{j} w+\mathrm{j} w_{0}\right) H_{i}\left(\mathrm{j} w+\mathrm{j} w_{0}\right)-Q_{r}\left(\mathrm{j} w-\mathrm{j} w_{0}\right) H_{i}\left(\mathrm{j} w-\mathrm{j} w_{0}\right)\right] \\ = & {\mathsf{π}}\left[I_{r}(\mathrm{j} w) H_{i}(\mathrm{j} w)-Q_{r}(\mathrm{j} w) H_{q}(\mathrm{j} w)\right] \times {\mathsf{π}}\left[\delta\left(w+w_{0}\right)+\delta\left(w-w_{0}\right)\right]+ \\ & {\mathsf{π}}\left[I_{r}(\mathrm{j} w) H_{q}(\mathrm{j} w)+Q_{r}(\mathrm{j} w) H_{i}(\mathrm{j} w)\right] \times \mathrm{j} {\mathsf{π}}\left[\delta\left(w+w_{0}\right)-\delta\left(w-w_{0}\right)\right] \\ = & F^{-1}\left\{{\mathsf{π}}\left[I_{r}(\mathrm{j} w) H_{i}(\mathrm{j} w)-Q_{r}(\mathrm{j} w) H_{q}(\mathrm{j} w)\right]\right\} \cos \left(w_{0} t\right)+F^{-1}\left\{{\mathsf{π}}\left[I_{r}(\mathrm{j} w) H_{q}(\mathrm{j} w)+Q_{r}(\mathrm{j} w) H_{i}(\mathrm{j} w)\right]\right\} \sin \left(w_{0} t\right) . \end{align*} $ | (9) |
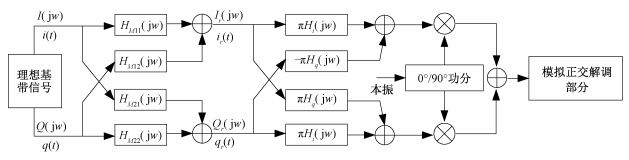
根据式(9)推导可知,通过将复通道传函正交分解成Hi(jw)和Hq(jw),能够将其分别映射到I、Q支路上,据此建立等效误差模型如图 4。
|
Download:
|
| 图 4 复通道误差到基带的映射 Fig. 4 Mapping of complex channel error to baseband | |
由图 4可见,复通道的传输函数映射到基带部分后的误差模型与调制器本身的误差模型从结构上是一致的,这里可将复通道的映射误差与调制器本身的系统误差进一步合并,合并后的结构与调制器本身的误差模型相同。
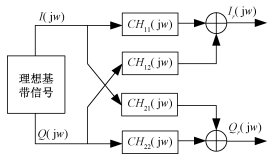
综上所述,可以得出结论,对于具有模拟正交调制解调的合成孔径雷达发射系统,完全可以等效为如图 5所示的系统误差模型。
|
Download:
|
| 图 5 发射系统的等效误差模型 Fig. 5 Equivalent error model of transmitting channel | |
其中CHmn(jw)(m, n=1, 2)为整个发射通道的系统传输函数模型。该模型完全包含了由于正交调制引入的幅相不平衡性误差,以及复通道引入的幅相误差。
2 预失真补偿方法预失真补偿的总体思路是设法将补偿网络的特性映射到系统的输入端,由于系统输入端即基带数字产生电路具有数字波形存储直读功能,通过对系统输入进行预失真,从而在不增加系统硬件的前提下即可实现对系统失真的校正。若宽带波形产生系统的传输函数矩阵H,系统输入端理想LFM信号矢量为X,则波形产生系统的输出信号矢量为HX;若期望得到的输出波形矢量为Y,则将输入信号矢量X预失真为H-1Y即可得到。采用这种方法进行失真补偿时,需要满足3个条件:1)系统传输函数矩阵的逆H-1存在。对于宽带系统而言,通常误差失真是缓变的且恶化并非特别严重,所以这个要求通常是能够满足的; 2)能产生期望的波形。由于本系统采用的是数字技术,所以能产生任意的带限信号; 3)能获得精确的系统传输函数矩阵H。目前,采用高性能的网络分析仪或数字示波器能精确地得到系统的传输函数。
下面首先建立SAR雷达发射系统的误差补偿模型,然后进一步推导预失真算法。
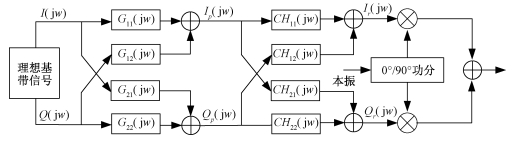
2.1 误差补偿模型的建立如果能够得到误差模型中系统的传输函数CHmn(m, n=1, 2),就能够推导出误差补偿函数Gmn(jw)(m, n=1, 2),进而对数字基带信号进行预失真补偿。具体的误差补偿原理框图如图 6所示。
|
Download:
|
| 图 6 正交调制误差补偿模型 Fig. 6 Error compensation model of quadrature modulation | |
Ip(jw)和Qp(jw)为经过预失真补偿后的基带信号。根据图 6所示,如果要求整个正交调制通道不产生幅相失真,需要满足如下关系
| $ \begin{align*} & {\left[\begin{array}{ll} C H_{11}(\mathrm{j} w) & C H_{12}(\mathrm{j} w) \\ C H_{21}(\mathrm{j} w) & C H_{22}(\mathrm{j} w) \end{array}\right]\left[\begin{array}{ll} G_{11}(\mathrm{j} w) & G_{12}(\mathrm{j} w) \\ G_{21}(\mathrm{j} w) & G_{22}(\mathrm{j} w) \end{array}\right]} \\ & =\exp \left(-\mathrm{j} w t_{0}\right) \boldsymbol{E}. \end{align*} $ | (10) |
其中E为2×2的单位矩阵,t0为系统延时,取t0为0,可以得到
| $ \begin{align*} & {\left[\begin{array}{ll} G_{11}(\mathrm{j} w) & G_{12}(\mathrm{j} w) \\ G_{21}(\mathrm{j} w) & G_{22}(\mathrm{j} w) \end{array}\right]=\left[\begin{array}{ll} C H_{11}(\mathrm{j} w) & C H_{12}(\mathrm{j} w) \\ C H_{21}(\mathrm{j} w) & C H_{22}(\mathrm{j} w) \end{array}\right]^{-1}} \\ & =A(\mathrm{j} w)\left[\begin{array}{cc} C H_{22}(\mathrm{j} w) & -C H_{12}(\mathrm{j} w) \\ -C H_{21}(\mathrm{j} w) & C H_{11}(\mathrm{j} w) \end{array}\right]. \end{align*} $ | (11) |
其中A(jw)=[CH11(jw)CH22(jw)-CH12(jw)CH21(jw)]-1,则可以得到补偿函数与系统传函的关系式
| $ \begin{align*} & G_{11}(\mathrm{j} w)=C H_{22}(\mathrm{j} w) A(\mathrm{j} w), \\ & G_{12}(\mathrm{j} w)=-C H_{12}(\mathrm{j} w) A(\mathrm{j} w), \\ & G_{21}(\mathrm{j} w)=-C H_{21}(\mathrm{j} w) A(\mathrm{j} w), \\ & G_{22}(\mathrm{j} w)=C H_{11}(\mathrm{j} w) A(\mathrm{j} w) . \end{align*} $$ $ | (12) |
则如果将输入基带信号预失真为ip(t)和qp(t), 即完成了系统的幅相不平衡预失真工作。
| $ i_{p}(t)=F^{-1}\left[I(\mathrm{j} w) G_{11}(\mathrm{j} w)+Q(\mathrm{j} w) G_{12}(\mathrm{j} w)\right]. $ | (13) |
| $ q_{p}(t)=F^{-1}\left[Q(\mathrm{j} w) G_{22}(\mathrm{j} w)+I(\mathrm{j} w) G_{21}(\mathrm{j} w)\right]. $ | (14) |
其中F-1[·]表示傅里叶反变换。
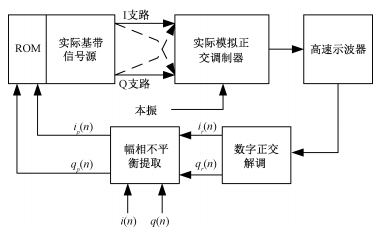
2.2 误差提取与补偿为得到系统误差传输函数CHmn(m, n=1, 2),可以建立如图 7所示的测试系统。
|
Download:
|
| 图 7 幅相不平衡性误差提取测试系统 Fig. 7 Amplitude and phase imbalance error extraction test system | |
具体过程是:首先向数字基带信号源中写入标准LFM基带信号i(n)和q(n),经过模拟正交调制后,利用高速示波器采集输出信号; 然后数字正交解调,得到ir(n)和qr(n),整个系统误差提取与补偿都是在数字离散域完成的。根据式(2)和式(3)即可建立如下关系
| $ I_{r}\left(\mathrm{e}^{\mathrm{j} \omega}\right)=I\left(\mathrm{e}^{\mathrm{j} \omega}\right) C H_{11}\left(\mathrm{e}^{\mathrm{j} \omega}\right)+Q\left(\mathrm{e}^{\mathrm{j} \omega}\right) C H_{12}\left(\mathrm{e}^{\mathrm{j} \omega}\right), $ | (15) |
| $ Q_{r}\left(\mathrm{e}^{\mathrm{j} \omega}\right)=Q\left(\mathrm{e}^{\mathrm{j} \omega}\right) C H_{22}\left(\mathrm{e}^{\mathrm{j} w}\right)+I\left(\mathrm{e}^{\mathrm{j} w}\right) C H_{21}\left(\mathrm{e}^{\mathrm{j} \omega}\right). $ | (16) |
将数字基带信号源内存中的标准LFM基带信号进行对调,即原来的I支路产生q(n),原来的Q支路产生i(n),再利用高速示波器采集输出信号,经过数字正交解调后,得到i′r(n)和qr′(n),再根据式(2)和式(3)可建立如下关系
| $ I_{r}^{\prime}\left(\mathrm{e}^{\mathrm{j} \omega}\right)=Q\left(\mathrm{e}^{\mathrm{j} \omega}\right) C H_{11}\left(\mathrm{e}^{\mathrm{j} \omega}\right)+I\left(\mathrm{e}^{\mathrm{j} \omega}\right) C H_{12}\left(\mathrm{e}^{\mathrm{j} \omega}\right), $ | (17) |
| $ Q_{r}^{\prime}\left(\mathrm{e}^{\mathrm{j} \omega}\right)=I\left(\mathrm{e}^{\mathrm{j} \omega}\right) C H_{22}\left(\mathrm{e}^{\mathrm{j} \omega}\right)+Q\left(\mathrm{e}^{\mathrm{j} w}\right) C H_{21}\left(\mathrm{e}^{\mathrm{j} \omega}\right). $ | (18) |
将式(15)~式(18)进行联立,即可解出系统传输函数。得到
| $ \begin{align*} & C H_{11}\left(\mathrm{e}^{\mathrm{j} \omega}\right)=\frac{I_{r}\left(\mathrm{e}^{\mathrm{j} \omega}\right) I\left(\mathrm{e}^{\mathrm{j} \omega}\right)-I_{r}^{\prime}\left(\mathrm{e}^{\mathrm{j} \omega}\right) Q\left(\mathrm{e}^{\mathrm{j} \omega}\right)}{I^{2}\left(\mathrm{e}^{\mathrm{j} \omega}\right)-Q^{2}\left(\mathrm{e}^{\mathrm{j} \omega}\right)}, \\ & C H_{12}\left(\mathrm{e}^{\mathrm{j} \omega}\right)=\frac{I_{r}^{\prime}\left(\mathrm{e}^{\mathrm{j} \omega}\right) I\left(\mathrm{e}^{\mathrm{j} \omega}\right)-I_{r}\left(\mathrm{e}^{\mathrm{j} \omega}\right) Q\left(\mathrm{e}^{\mathrm{j} \omega}\right)}{I^{2}\left(\mathrm{e}^{\mathrm{j} \omega}\right)-Q^{2}\left(\mathrm{e}^{\mathrm{j} \omega}\right)}, \\ & C H_{21}\left(\mathrm{e}^{\mathrm{j} \omega}\right)=\frac{Q_{r}\left(\mathrm{e}^{\mathrm{j} \omega}\right) I\left(\mathrm{e}^{\mathrm{j} \omega}\right)-Q_{r}^{\prime}\left(\mathrm{e}^{\mathrm{j} \omega}\right) Q\left(\mathrm{e}^{\mathrm{j} \omega}\right)}{I^{2}\left(\mathrm{e}^{\mathrm{j} \omega}\right)-Q^{2}\left(\mathrm{e}^{\mathrm{j} \omega}\right)}, \\ & C H_{22}\left(\mathrm{e}^{\mathrm{j} \omega}\right)=\frac{Q_{r}^{\prime}\left(\mathrm{e}^{\mathrm{j} \omega}\right) I\left(\mathrm{e}^{\mathrm{j} \omega}\right)-Q_{r}\left(\mathrm{e}^{\mathrm{j} \omega}\right) Q\left(\mathrm{e}^{\mathrm{j} \omega}\right)}{I^{2}\left(\mathrm{e}^{\mathrm{j} \omega}\right)-Q^{2}\left(\mathrm{e}^{\mathrm{j} \omega}\right)}. \end{align*} $ | (19) |
再由公式(12)即可完成基带信号补偿函数的提取,利用式(13)和式(14)完成预失真补偿。
3 实际系统验证对于SAR雷达激励信号的幅相不平衡误差,主要可以通过测量实际信号的本振泄漏以及镜频抑制度进行有效评估。同时,为进一步说明幅相不平衡误差对雷达脉冲压缩的影响,需要分析雷达激励信号的相位误差以及脉冲压缩特性。下面针对实际的SAR雷达发射通道,利用第2节和第3节分析给出的幅相不平衡预失真校正方法,对系统的幅相不平衡误差进行提取和补偿,最后给出校正补偿的测试结果。
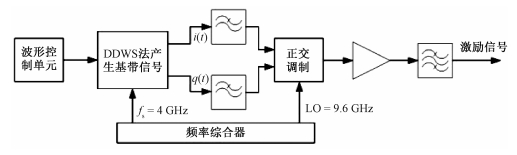
3.1 系统实现为实现分辨率优于0.1 m的高分辨率,系统要产生中心频率9.6 GHz、最大瞬时带宽2 GHz的宽带雷达激励信号。系统实现的技术方案是采用直接变频架构,将基带IQ信号直接正交调制到中心频率为9.6 GHz的载波上,完成宽带激励信号的产生。系统实现的原理如图 8所示。
|
Download:
|
| 图 8 X波段宽带激励信号的产生 Fig. 8 X-band broadband excitation generation | |
数字基带信号源采用波形存储直读法产生双路I、Q基带信号,其采样时钟为4 GHz,产生幅度一致及相位正交的双路I、Q基带信号,每路实信号的带宽为1 000 MHz,通过模拟低通滤波器后,由本振LO=9.6 GHz进行正交调制,直接上变频到X波段,产生系统要求的(9.6±1) GHz的SAR激励信号。电路结构简单,具有极低的功耗,电路稳定性高。但是,其主要技术关键点在于:由于工作频率较高,X波段的模拟正交调制器很难做到接近理想的I、Q一致性,其镜频和载漏抑制很难满足指标要求,使得最终产生激励信号的谱质不能满足系统要求,需要利用本文提出的预失真校正方法对整个发射链路幅相误差进行补偿。
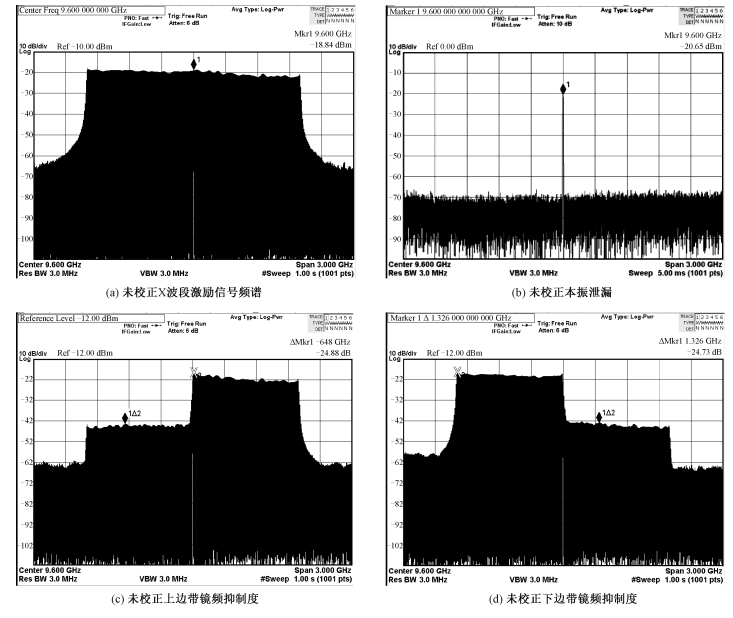
3.2 校正前后结果分析比较由于镜频信号在频域上位于激励信号的带宽之内,对于镜频信号的测试可以通过利用数字基带源产生正常时域LFM信号的一半来完成。在未经过幅相不平衡校正时,产生的X波段激励信号镜频抑制度和载频泄漏如图 9所示。
|
Download:
|
| 图 9 未校正X波段激励信号频谱分析 Fig. 9 Analysis of uncorrected X-band excitation signal | |
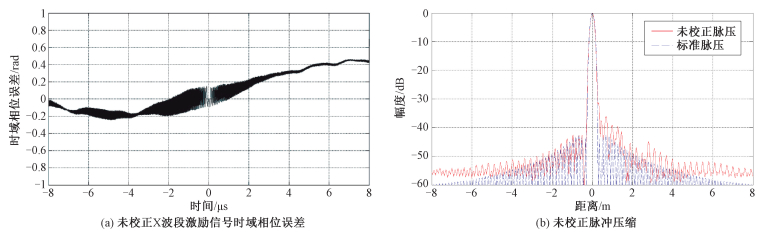
由图 9可见,镜频抑制度≤25 dBc, 本振泄漏≤-20 dBm,该信号的时域相位误差以及汉明窗加权的脉冲压缩特性如图 10所示。
|
Download:
|
| 图 10 未校正X波段激励信号误差分析 Fig. 10 Error analysis of uncorrected X-band excitation | |
由图 10可见,时域相位误差0.5 rad,脉冲压缩旁瓣抑制度36 dBc,噪声基底相对标准脉压结果抬高约5 dB。最终会影响图像信噪比,恶化系统性能。另外,从时域相位误差图中可以看到,整个误差曲线上存在波形的震荡,这也是镜频干扰引起的。
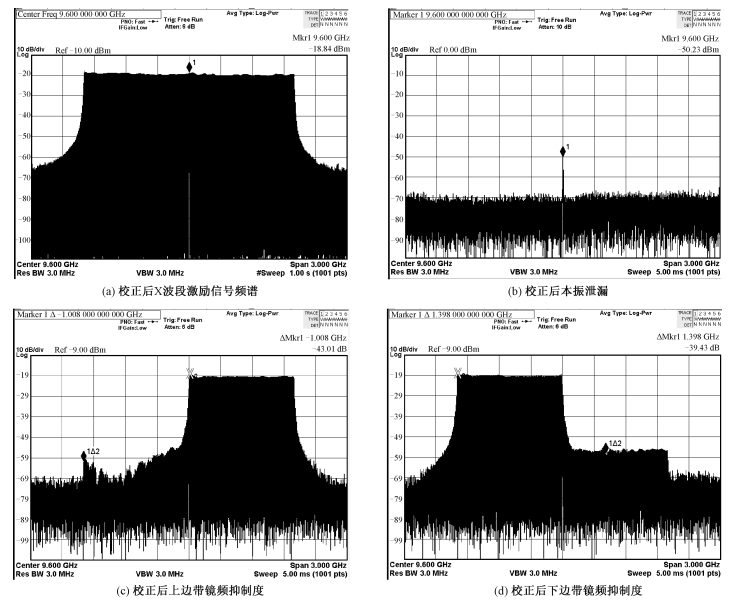
首先利用偏置电路调整基带I、Q的直流偏置,使得载频泄漏降低为-50 dBm(见图 11(b));然后利用第3节所述的幅相不平衡补偿方法提取实际系统的误差补偿函数,来完成基带信号的数字预失真;最后对雷达激励信号输出时频特性进行测试,如图 11(c)和11(d)所示。
|
Download:
|
| 图 11 校正后X波段激励信号频谱分析 Fig. 11 Analysis of X-band excitation after correction | |
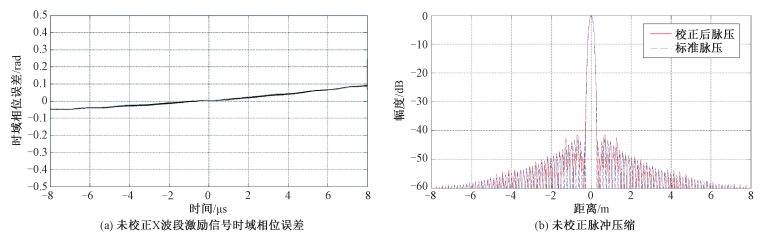
可见镜频抑制度大于39 dBc,通过对比校正前后,镜频抑制度得到了很大改善,也进一步优化了输出激励信号的谱质。对输出的激励信号进行相位误差分析,结果见图 12。
|
Download:
|
| 图 12 校正后X波段激励信号误差分析 Fig. 12 Error analysis of X-band excitation after correction | |
可见时域相位误差在±0.1 rad以内,并且误差曲线上的震荡明显减小,说明镜频干扰得到了有效抑制,信号具有非常优良的调频斜率线性度,其脉冲压缩结果(实线)与理想脉压(虚线)基本重合,峰值旁瓣比大于42 dBc。
表 1是校正前后相关主要性能指标测试结果的对比。可以看到校正后发射信号主要性能指标都有很大改善。
|
|
表 1 校正前后主要指标测试结果对比 Table 1 Comparison of test results before and after correction |
SAR宽带雷达激励发射通道设计中,模拟正交调制是最为常用也是非常重要的技术手段之一。随着雷达分辨率越来越高,雷达系统瞬时带宽设计得越来越大,模拟正交调制的幅相不平衡特性并不能完全依靠器件本身的对称特性来保证。本文论述了一种应用在宽带雷达发射系统中的正交调制幅相不平衡数字预失真校正方法。通过对雷达发射通道进行完整的误差建模,在模型的基础上提出预失真补偿算法,并通过搭建测试系统对系统的误差函数进行提取,完成系统的幅相误差校正工作。最后针对实际X波段的SAR雷达发射通道,利用预失真算法进行整个发射链路的幅相误差补偿,给出校正前后的测试对比结果。通过测试表明算法的有效性,最终提高了雷达激励信号的谱质,提升了雷达系统性能。
| [1] |
Brenner A R, Essen H, Stilla U. Representation of stationary vehicles in ultra-high resolution SAR and turntable ISAR images[C]//EUSAR 2012; 9th European Conference on Synthetic Aperture Radar. Nuremberg, Germany. VDE: 147-150.
|
| [2] |
El-Arnauti G, Saalmann O, Brenner A R. Ultra-high resolution airborne experiments with a new Ka-band SAR sensor[C]//2017 European Radar Conference (EURAD). October 11-13, 2017. Nuremberg, Germany. IEEE, 2017: 409-412. DOI: 10.23919/eurad.2017.8249234.
|
| [3] |
Dupuis X, Martineau P. Very high resolution circular SAR imaging at X band[C]//2014 IEEE Geoscience and Remote Sensing Symposium. Quebec City, QC, Canada. IEEE, : 930-933. DOI: 10.1109/IGARSS.2014.6946578.
|
| [4] |
Mishra S, Singh N, Dhar J, et al. A GaAs based miniaturized C-band double balanced resistive IQ modulator for synthetic aperture radar (SAR) applications[C]//2019 IEEE Recent Advances in Geoscience and Remote Sensing: Technologies, Standards and Applications. Kochi, India. IEEE, : 57-60. DOI: 10.1109/TENGARSS48957.2019.8976064.
|
| [5] |
Yahav N, Efendowicz A. Broadband high linearity IQ modulator for direct conversion transmitters[C]//2016 46th European Microwave Conference (EuMC). London, UK. IEEE: 1019-1022.
|
| [6] |
Zhu Z W, Leung H, Huang X P. Challenges in reconfigurable radio transceivers and application of nonlinear signal processing for RF impairment mitigation[J]. IEEE Circuits and Systems Magazine, 2013, 13(1): 44-65. Doi:10.1109/MCAS.2012.2237143 |
| [7] |
Luo J, Kortke A, Keusgen W, et al. A novel adaptive calibration scheme for frequency-selective I/Q imbalance in broadband direct-conversion transmitters[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2013, 60(2): 61-65. Doi:10.1109/TCSⅡ.2012.2235735 |
| [8] |
Khandelwal A, Verma A. A novel gain, phase and offset calibration scheme for wideband direct-conversion transmitters[C]//2015 IEEE 81st Vehicular Technology Conference. Glasgow, UK. IEEE, : 1-5. DOI: 10.1109/VTCSpring.2015.7145633.
|
| [9] |
Fawzy A, Sun S M, Lim T J, et al. Iterative learning control for pre-distortion design in wideband direct-conversion transmitters[C]//GLOBECOM 2020: 2020 IEEE Global Communications Conference. Taipei, China. IEEE, : 1-6. DOI: 10.1109/GLOBECOM42002.2020.9322378.
|
| [10] |
Zhu Z W, Huang X P, Leung H. Joint I/Q mismatch and distortion compensation in direct conversion transmitters[J]. IEEE Transactions on Wireless Communications, 2013, 12(6): 2941-2951. Doi:10.1109/TCOMM.2013.050313.121256 |
| [11] |
Zhu Z W, Huang X P, Caron M, et al. Blind self-calibration technique for I/Q imbalances and DC-offsets[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2014, 61(6): 1849-1859. Doi:10.1109/TCSI.2013.2290826 |
| [12] |
Arriaga-Trejo I A. Estimation of the channel and I/Q imbalances with zero correlation zone sequences and superimposed training[C]//2019 IEEE International Conference on Microwaves, Antennas, Communications and Electronic Systems. Tel-Aviv, Israel. IEEE, : 1-6. DOI: 10.1109/COMCAS44984.2019.8958069.
|
| [13] |
Huang X J, Zhang J A, Guo Y J. Joint transmitter and receiver I/Q imbalance estimation in presence of carrier frequency offset[C]//2015 15th International Symposium on Communications and Information Technologies (ISCIT). Nara, Japan. IEEE, : 209-212. DOI: 10.1109/ISCIT.2015.7458344.
|
| [14] |
陈雷, 岳光荣, 唐俊林, 等. 基于数字预失真的发射机I/Q不平衡矫正[J]. 电子与信息学报, 2017, 39(4): 847-853. Doi:10.11999/JEIT160581 |
| [15] |
陆必应, 梁甸农. 大时带积线性调频信号源幅相误差分析与校正[J]. 现代雷达, 2004, 26(10): 38-40, 60. Doi:10.16592/j.cnki.1004-7859.2004.10.012 |
 2024, Vol. 41
2024, Vol. 41 


