在底部或内部加热足够强时,孔隙介质内的流体会因重力失稳而发生自然对流[1-2]。与外加压力驱动和控制的强迫对流不同,自然对流由流体自身热胀冷缩伴随的热浮力驱动,其动力学演化是传热与流动内在耦合的结果。
孔隙自然对流问题研究具有重要的工程意义和学术价值。一方面,地下孔隙岩石中的流体流动是油气、地下水、地热能开发与二氧化碳封存等大量工程实践[3-8]的基础。岩石中的流体是否发生自然对流以及自然对流发生后的形态和强度,对实际工程的施工和效果往往具有至关重要的影响。另一方面,孔隙自然对流呈现复杂的空间形态变化和丰富的时间演化行为,成为流动稳定性、分岔、混沌和湍流机理等非线性流体动力学领域[9-10]高度关注的研究对象。例如,孔隙自然对流走向混沌的动力学路径与纯流体自然对流存在本质区别[11],为认识自然对流的普遍规律和基本机制提供了深刻的启示。
前人对孔隙自然对流已开展大量研究工作,其中对孔隙介质方腔内由底部加热而产生的二维自然对流研究最为集中。孔隙自然对流的加热强度由无量纲Rayleigh数(Ra)表征。在底部加热情形,Ra正比于对流层厚度、上下边界温差、流体热膨胀系数和渗透率,而反比于流体运动学黏度和热扩散率。线性稳定性分析[2]证明,当Ra增加到最小临界值4π2时,水平方向无界的均匀孔隙层从流体静止的热传导状态失稳,开始自然对流。最先发育的自然对流形态是宽度等于孔隙层厚度的二维对流环,等价于侧边界绝热的孔隙方腔内二维自然对流。在此基础上,继续追踪方腔内二维自然对流随Ra增加的动力学行为就成为一个自然的选择。当然,实际对流系统在高Ra条件下可能发展成三维对流形态,但二维自然对流总可看作是三维自然对流在第3维尺度减小时的渐近情形,因而仍然具有明确的物理意义。相对于对计算资源要求极为苛刻的三维模拟计算,计算简单又不失物理意义的二维模拟更利于开展细致深入的研究工作,从而揭示控制自然对流的复杂物理机制。
尽管前人对方腔内二维孔隙自然对流问题做了大量研究,但仍然不够充分。受早期计算条件限制,前人研究工作主要侧重于中心对称(水平波数与垂向波数之和为偶数)对流模态的时空演化动力学机制[12-17],仅对个别Ra取值的特例讨论过奇数波数与模态的贡献和影响[11, 18-19]。因此,现有研究结果既不能完整刻画实际孔隙自然对流系统的动力学行为,也无法直接应用于实际工程。例如,最具工程意义的无量纲热流(Nusselt数,Nu)随无量纲温差(Ra)的变化关系,迄今仅在稳态对流开始阶段存在近似公式[5, 20-21]。
本研究对底部加热孔隙介质方腔内二维自然对流进行模态完备(同时包含奇偶波数和模态)的系统性数值模拟,首次得到自然对流从发生到走向混沌的完整动力学演化路径。本文首先对采用的数值模型及其求解算法作简要介绍,而后详细描述模拟结果,讨论自然对流空间形态变化的成因与时间振荡的特征,以及计算热流和振荡主频的公式拟合,以便于实际工程设计和应用。
1 数值模型及其求解算法考虑边长为l的正方形区域,内部为流体饱和均匀孔隙介质。设定区域四周均为不可渗透(法向速度为零)边界,2个侧面边界绝热(水平温度梯度为零),且下边界温度T1恒大于上边界温度T0(底部加热)。相应地,Ra定义为
| $ R a=\frac{g \alpha\left(T_1-T_0\right) l K}{\nu \kappa_m}, $ | (1) |
其中:g为重力加速度,K和κm分别为孔隙介质渗透率和等效热扩散率,而α和ν分别为流体热膨胀系数与运动学黏度。
设孔隙介质等效比热与流体比热之比为C,并分别以l、T1-T0、κm/l、l2C/κm作为特征长度、温度、速度和时间对控制方程组无量纲化,则无量纲控制方程组[18]在直角坐标系可写成
| $ \begin{gathered} \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0, \end{gathered} $ | (2) |
| $ u=-\frac{\partial p}{\partial x}, $ | (3) |
| $ v=-\frac{\partial p}{\partial y}+R a \theta, $ | (4) |
| $ \frac{\partial \theta}{\partial t}+u \frac{\partial \theta}{\partial x}+v \frac{\partial \theta}{\partial y}-v=\frac{\partial^2 \theta}{\partial x^2}+\frac{\partial^2 \theta}{\partial y^2}, $ | (5) |
其中:无量纲坐标x和y的正向分别为水平向右和垂直向上,u、v和p分别代表水平达西速度、垂向达西速度和孔隙压力,而偏离温度θ=T-Tc表示自然对流发生后温度T与传导温度解Tc=-y+1/2的偏离。
将达西定律式(3)和式(4)分别代入到连续性方程(2)和能量方程(5),可消去达西速度,并得到偏离温度和孔隙压力满足的耦合方程组
| $ \frac{\partial^2 p}{\partial x^2}+\frac{\partial^2 p}{\partial y^2}=R a \frac{\partial \theta}{\partial y}, $ | (6) |
| $ \frac{\partial \theta}{\partial t}-\frac{\partial p}{\partial x} \frac{\partial \theta}{\partial x}-\left(\frac{\partial p}{\partial y}-R a \theta\right)\left(\frac{\partial \theta}{\partial y}-1\right)=\frac{\partial^2 \theta}{\partial x^2}+\frac{\partial^2 \theta}{\partial y^2}. $ | (7) |
因此,偏离温度和孔隙压力构成数值求解的基本未知量,其满足的边界条件为
| $ \begin{cases}\frac{\partial \theta}{\partial x}=0, \frac{\partial p}{\partial x}=0 & {\text { at }} x= \pm \frac{1}{2}, \\ \theta=0, \frac{\partial p}{\partial y}=R a \theta & {\text { at }} y= \pm \frac{1}{2}.\end{cases} $ | (8) |
为求解控制方程(6)和(7),将基本未知量对空间自变量作双重傅里叶级数展开[11-12]。容易验证,展开成如下形式的偏离温度和孔隙压力
| $ \theta=\sum\limits_{m=0}^M \sum\limits_{n=1}^N a_{m n} \cos m \pi\left(x+\frac{1}{2}\right) \sin n \pi\left(y+\frac{1}{2}\right), $ | (9) |
| $ \begin{gathered} p=-\sum\limits_{m=0}^M \sum\limits_{n=1}^N\left[a_{m n} \frac{n R a}{\left(m^2+n^2\right) \pi} \cos m \pi(x+\right. \\ \left.\left.\frac{1}{2}\right) \cos n \pi\left(y+\frac{1}{2}\right)\right], \end{gathered} $ | (10) |
能够自动满足动量方程(6)和边界条件(8)。将级数展开的偏离温度和孔隙压力一同代入能量方程(7),就得到展开系数amn满足的非线性方程。从该方程解出展开系数是数值计算的核心内容。展开系数在稳态对流情形只随Ra变化,而在瞬态对流情形还随时间变化。
容易证明,仅由m+n为偶数的模态叠加而成的偏离温度场和孔隙压力场满足
| $ \theta(x, y)=-\theta(-x, -y), $ | (11) |
| $ p(x, y)=p(-x, -y) . $ | (12) |
这种偏离温度中心反对称而孔隙压力中心对称的自然对流解习惯上称作中心对称解。本研究计算中包含m+n取奇数与偶数的全部模态。
本研究采用伽辽金法[16]求解稳态对流问题。将控制方程对空间自变量积分,并利用三角函数的正交性化简得到非线性代数方程组,再利用牛顿法迭代解出展开系数。采用伽辽金法的优势在于计算精度高,且便于随后对稳态级数解进行稳定性检验。
瞬态对流问题虽然原则上也可以采用伽辽金法求解,但对高阶模态发育充分的高Ra问题,该方法计算速度过慢导致效率过低[22]。本研究采用配点伪谱法[11, 13, 22]进行瞬态计算,并利用快速傅里叶变换将物理空间内乘积形式的非线性项转换为系数相空间的点积,能够获得远高于伽辽金法的计算效率。对于瞬态问题涉及的时间变化,本研究采用数值差分处理。为平衡计算精度和效率,数值计算中对非线性项采用二阶显式Adams差分格式[23],而对线性项采用Crank-Nicholson格式[23]。
瞬态自然对流计算需要提供合适的初始条件。本研究的一个主要目标是,在Ra单调增加的情形下,获得孔隙自然对流模态完备的动力学演化完整路径。为保证模态完备和路径完整,所有瞬态计算的初始条件都包含全模态扰动成分。具体做法是,将一个Ra的计算终态,叠加一个振幅很小但模态完备的扰动之后,再作为初始条件提供给Ra加一个增量后的瞬态计算。扰动成分来自于Ra=1 300时充分发育的混沌振荡解,但将对应的展开系数振幅缩小为1 ‰。实际计算表明,这样选择初始条件可以有效避免进入错误的演化路径。在自然对流演化的很多阶段,中心对称解是稳定存在的计算终态,以此为初值相继计算Ra增加后的对流,往往会一直保持中心对称[11, 13, 18-19]。如果计算初值中导致中心对称解失稳的模态系数基本为零,即使中心对称解在物理上已不再稳定,在数值计算中也很难发现已进入中心对称解不稳定的错误路径。在初始条件中叠加模态完备的扰动能够避免这种情况发生。
在解出基本未知量后,达西速度可以利用达西定律式(3)和式(4)计算,而通过下边界的无量纲热流可由Nu表示为
| $ N u=-\left.\int_{-\frac{1}{2}}^{\frac{1}{2}} \frac{\partial \theta}{\partial y}\right|_{y=-\frac{1}{2}} {\mathrm{~d}} x+1=-\sum\limits_{n=1}^N n \pi a_{0 n}+1 . $ | (13) |
显然,Nu在热传导状态等于1,而在振荡对流状态会随时间变化。
为验证采用的数值模型和求解方法可靠性,本研究首先与前人数值模拟结果进行对比。在限定只存在中心对称模态并且级数展开阶次相同的条件下,本文模型得到了与Graham和Steen[15]一致的结果。例如,Graham和Steen[15]报告最早的准周期对流是发生在Ra=505基频分别为103和27.7的双频振荡,而本研究得到准周期始于Ra=505.8基频为103.04和27.68的双频振荡。
本文后面给出的数值结果都是级数展开至64阶计算的,瞬态计算的时间步长一律取作5×10-6。经过多个典型Ra取值检验,Nu计算结果与展开阶次加倍或时间步长减半后的结果相比差别小于1 ‰。说明空间截断与时间离散误差对本文结果的影响可以忽略不计。
2 数值模拟结果与讨论 2.1 稳态自然对流及其稳定性孔隙介质方腔内的流体在Ra大于Ra0=4π2后开始自然对流。开始阶段的对流是稳定的稳态对流,既不随时间变化,又能抵抗扰动。这一阶段的对流解可以通过略去控制方程中时间导数项求解稳态问题得到。但随着Ra的增加,得到的稳态解是否能够稳定存在,决定了其能否代表实际发生的自然对流。不稳定的稳态解只有理论上的意义,在实际物理世界不能真实存在,而会被瞬态解所取代。
检验稳态对流解的稳定性,即是检验抵抗扰动的能力。为此,将带扰动成分的对流解写成稳态解与小扰动叠加的形式
| $ \left\{\begin{array}{l} \theta=\theta_{\mathrm{s}}+\tilde{\theta}, \\ p=p_{\mathrm{s}}+\tilde{p}, \end{array}\right. $ | (14) |
其中:
| $ \left\{\begin{array}{l} \tilde{\theta}=\mathrm{e}^{\sigma t} \sum\limits_{m=0}^M \sum\limits_{n=1}^N b_{m n} \cos m \pi\left(x+\frac{1}{2}\right) \sin n \pi\left(y+\frac{1}{2}\right), \\ \tilde{p}=-\mathrm{e}^{\sigma t} \sum\limits_{m=0}^M \sum\limits_{n=1}^N\left[\frac{n R a}{\left(m^2+n^2\right) \pi} b_{m n} \cos m \pi\left(x+\frac{1}{2}\right) \cos n \pi\left(y+\frac{1}{2}\right)\right], \end{array}\right. $ | (15) |
与稳态对流解叠加之后仍然满足动量方程和边界条件。将式(14)代入到能量方程(7),并忽略非线性高阶小量,可得到线性稳定性方程
| $ \begin{aligned} & \frac{\partial \tilde{\theta}}{\partial t}-\frac{\partial p}{\partial x} \frac{\partial \tilde{\theta}}{\partial x}-\frac{\partial \theta}{\partial x} \frac{\partial \tilde{p}}{\partial x}-\left(\frac{\partial p}{\partial y}-R a \theta\right) \frac{\partial \tilde{\theta}}{\partial y}- \\ & \left(\frac{\partial \theta}{\partial y}-1\right)\left(\frac{\partial \tilde{p}}{\partial y}-R a \tilde{\theta}\right)=\frac{\partial^2 \tilde{\theta}}{\partial x^2}+\frac{\partial^2 \tilde{\theta}}{\partial y^2}. \end{aligned} $ | (16) |
将级数展开的扰动和已经解出的被检验稳态级数解代入式(16),并对空间自变量积分,同时利用三角函数的正交性化简,便可得到小扰动随时间变化的特征方程
| $ \sigma {\boldsymbol{I B}}={\boldsymbol{A B}}, $ | (17) |
其中:I是单位矩阵,B是小扰动展开系数组成的向量,而方阵 A只依赖于被检验稳态解的展开系数。求解式(17)定义的特征值问题,若所有特征值(σ)的实部均为负值,则表示扰动随时间衰减,即稳态对流是稳定的。反之,当任一个特征值的实部大于零时,就表明扰动随时间增长,即稳态对流已失稳。
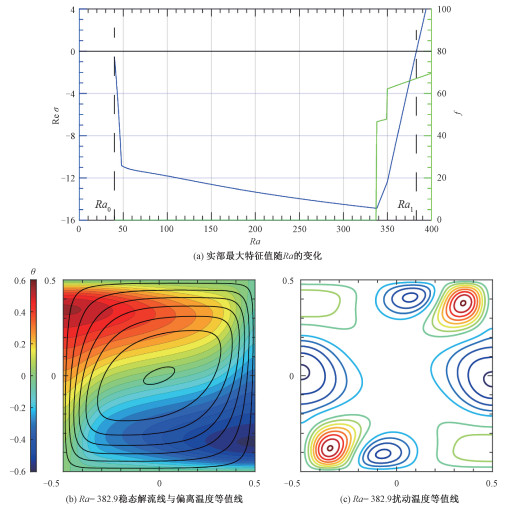
图 1(a)给出了实部最大特征值随Ra增加而变化的计算结果。当Ra小于337时,特征值为负实数,表明扰动会作单调指数衰减。在Ra介于337~382.9时,特征值为实部取负值的复数,反映扰动以振荡的形式衰减,振荡频率由特征值虚部除以2π给出。特别地,当Ra=Ra1=382.9时,特征值实部为零,表明对应的稳态解(图 1(b))开始失稳,失稳扰动的振荡频率为67.09。导致稳态解失稳的扰动可通过计算对应的特征向量得到,其空间形态由图 1(c)给出。
|
Download:
|
| 图 1 稳态解及其稳定性 Fig. 1 Steady-state solution and stability | |
从图 1(b)可以看到,偏离温度场满足式(11)表示的中心反对称性,如左上方正温度区与右下方负温度区的对称。这是因为稳态对流解全由中心对称模态叠加而成。图 1(b)显示的流线对应顺时针流动。流体自右向左流经方腔底部,由底部加热产生的热浮力驱动流体沿左侧边界上升,而后在方腔顶部冷却后再沿右侧边界流回底部,形成循环。流线和等温线向边界附近集中是速度边界层和热边界层的直观表现。Ra小于Ra1的稳态对流形态与图 1(b)定性一致,只是温度分布更均匀、流动更缓慢。
图 1(c)所示的扰动温度场显然不满足式(11),如左下角和右上角都是正温度区,这种绕方腔中心旋转180°后温度相等的对称性,是m+n取奇数模态的特征。因此稳态解失稳后将同时包含m+n取奇数与偶数的模态,即进入混合模态对流。
图 1(c)显示沿方腔四周边界分布2组对称的环状温度异常,每组包括相间出现的2个高温和2个低温异常。这些温度异常是由边界层失稳形成的。因为边界层内的流体正在进行图 1(b)所示的稳态自然对流,流体携带温度异常沿方腔边界作顺时针流动,形成行波。图 1(c)所示为波数为4的行波形态。
根据稳态对流及其稳定性分析,可以推断在Ra>382.9后,自然对流由稳态中心对称解演变成混合模态振荡解,初始振荡频率约为67,而空间形态为波数k=4的行波与中心对称稳态解的复合。这些推断得到了瞬态自然对流解的验证。
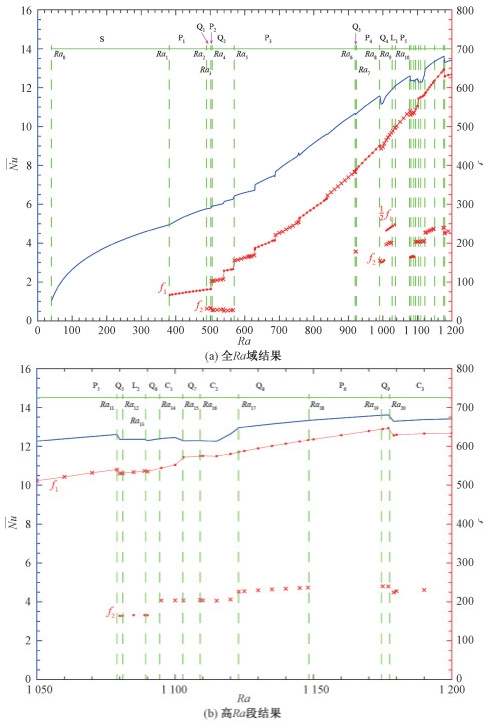
2.2 自然对流的动力学演化路径本研究通过单调递增Ra数值计算得到的Nu长时间积分平均值与振荡频率演化由图 2给出。方腔内的孔隙自然对流从发生到Ra=1 200,呈现了复杂的动力学演化过程。在稳态对流阶段(S)之后,瞬态对流在单频(P)、准周期(Q)、锁频(L)和混沌(C)多种振荡类型间反复交替。根据振荡类型的不同,整个动力学演化路径可分为21个不同阶段,包括1个稳态对流阶段、6个单频振荡阶段、9个准周期振荡阶段、2个锁频共振阶段和3个非周期混沌振荡阶段。不同阶段的分界Ra取值由表 1列出。
|
Download:
|
| 图 2 单调增加Ra计算得到的Nu时间积分平均值与振荡频率演化 Fig. 2 Evolution of the time-integral average value and oscillation frequencies of Nu calculated by monotonically increasing Ra | |
|
|
表 1 自然对流演化的不同阶段及其分界Rayleigh数 Table 1 Different stages with their bounding Rayleigh numbers of the natural convection evolution |
图 2中f1称作主频[12],是从稳态解失稳开始可以持续追踪的频率。在所有的单频振荡阶段,频谱只包含主频整数倍的成分。频率f2为主频之外的另一个振荡频率。当f1与f2之比为无理数时,以f1和f2为基底通过整系数线性组合形成双频准周期振荡频谱的全部成分,所以频谱是f1和f2作基频的离散谱。当f1与f2之比为有理数时,双频振荡发生共振,形成锁频振荡,频谱成分为f1与f2最大公约数的整数倍。在混沌振荡阶段,频谱包含连续分布的频率成分(非周期振荡),图 2在混沌区给出的f1与f2是从混沌区外追踪识别的。
在Ra=1 006附近,f1振荡通过次谐分岔[18] (周期加倍)而生成减半的新频率,如图 2所示。该频率先与f2共同作基频形成Q4后半段的准周期振荡,又在f2消失后与f1形成锁频段L1,最后通过另一个次谐分岔消失。
图 2中带“×”的频率表示对应的振荡是仅由中心对称模态构成,而带点的频率表示对应的振荡是混合模态。显然,稳态自然对流失稳后最先发生的是混合模态单频振荡。图 2中f1曲线由混合模态段与中心对称段交替连接而成。不同模态的交替是由行波波数改变造成的。随着Ra增加,f1曲线各段分别对应行波波数从4顺序增加到14的不同阶段。波数改变时,多数伴随f1值和Nu值的不光滑跃变。
本文得到的自然对流演化路径与前人认识存在定性的区别。Graham和Steen[15]得到中心对称解随Ra增加的演化路径为行波波数按5、3、7、9的顺序变化。根据这一结果和包含全部模态的自然对流在Ra=383附近开始行波波数为4的振荡,Graham和Steen[18]推断自然对流将按行波波数4、5、3、6、7、8、9、10的顺序演化。本文结果表明,行波波数为3的演化阶段不能稳定存在(不能抵抗模态完备的扰动),所以整个演化路径表现为行波波数的单调顺序递增。
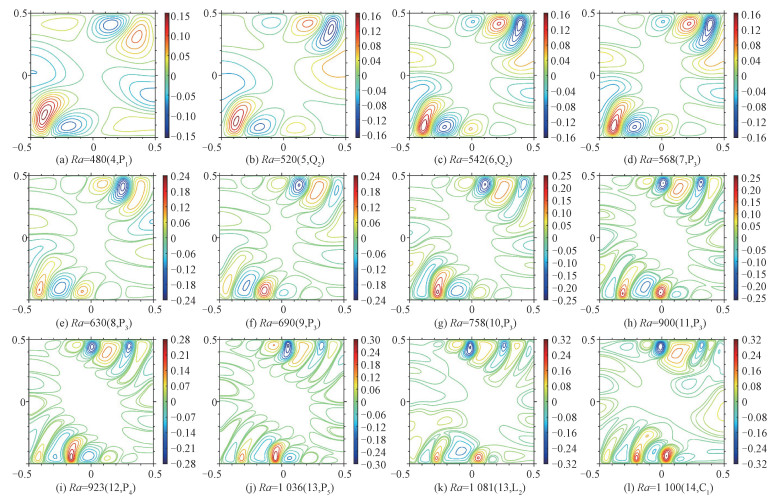
2.3 瞬态自然对流的空间形态演化数值模拟得到的瞬态自然对流解同时包含对流形态的空间变化和随时间的振荡。行波波数变化是空间形态变化的主要控制因素,但行波是在平均温度场背景上的振荡。为突出显示不同行波波数对应的振荡温度场结构,选择不同Ra取值的计算终态附近瞬时温度解减去对总计算时间后半段(跨过初始扰动演化阶段)进行平均的温度场,得到图 3所示振荡温度场随Ra的形态变化。
|
Download:
|
| 图 3 振荡温度场行波结构随Ra的变化(对应的行波波数k与演化阶段在括号内标出) Fig. 3 Variation of traveling wave structure of oscillating temperature field with Ra (corresponding traveling wave number k and evolution stage are indicated in parentheses) | |
图 3清楚地反映了温度异常数目与行波波数的对应关系以及行波振荡的空间对称性。Ra=480时的行波波数4单频混合模态振荡,由图 3(a)的温度异常数个数和不对称温度分布清楚地指示。类似地,行波波数分别为偶数6、8、10、12和14的图 3(c)、3(e)、3(g)、3(i)和3(l)均对应温度不对称分布的混合模态对流。而图 3(b)显示由波数5行波主导的中心反对称温度分布,则与图 2(a)给出的Ra=520时双频准周期振荡全由中心对称模态构成一致。与此类似,行波波数分别为奇数7、9、11和13的图 3(d)、3(f)、3(h)和3(j)均为中心对称模态对流。图 3(k)对应于Ra=1 081的锁频解,尽管主频是行波波数为13的中心对称模态,但形成锁频的另一个基频不是中心对称模态(图 2(b)),导致叠加后不对称的混合模态锁频振荡。
图 3显示的对流形态演化并非只受行波波数控制。这可由振荡主频随行波波数的定量变化揭示。行波由流体的单环顺时针背景流动携带温度异常传播而形成,所以行波振荡频率正比于波数,比例系数为背景流动速度。在行波波数发生变化前后,可以假设背景流动速度不变,从而波数变化前后的行波振荡频率比应等于波数比。表 2给出了这2个比值在行波波数变化时的对比,其中的振荡主频由临近的计算值插值得到。表 2表明,在最初的3个行波波数变化处,行波振荡主频比与波数比非常一致,但随后振荡主频比显著低于波数比,且差距逐渐增大,直至最后振荡主频与波数呈相反的变化趋势。
|
|
表 2 瞬态自然对流行波波数变化前后波数比与振荡主频比的比较 Table 2 Comparison between wave number ratio and primary frequency ratio before and after a change in traveling wave number of the transient natural convection solutions |
表 2列出的定量比较提示,在行波波数变化之外,控制对流形态演化的物理要素在Ra高于567之后逐渐加强。从图 3可以看出,Ra高于568之后,最左侧底部边界热异常对应的等值线逐渐趋向于竖直方向,即热异常逐渐趋向于热柱形态。Graham和Steen[18]指出,Ra高于700之后,热柱发育导致自然对流近似符合经典边界层分析给出的标度率,与热柱发育前只由行波控制的振荡对流不服从边界层标度率形成鲜明的对比。本文结果表明,热柱的影响在更低的Ra条件下已开始显现。热柱与行波波数共同控制了自然对流空间形态的演化。
2.4 自然对流随时间振荡的不同特征随时间振荡的自然对流瞬态解包括偏离温度、孔隙压力和达西速度在整个求解区域的振荡,但分析不同类型振荡的特征,并不需要考虑所有物理量的全部自由度。通常情况下,仅分析一个自由度的时间行为即可[24],因为整个物理系统的振荡具有内在的统一性。本节通过分析数值模拟得到的Nu的时间变化,讨论不同振荡类型的特征。在2.2节,根据单频、准周期、锁频和混沌振荡的不同类型,将自然对流的动力学演化路径分成不同的阶段。显然,这些振荡类型的准确区分是演化阶段划分的关键。
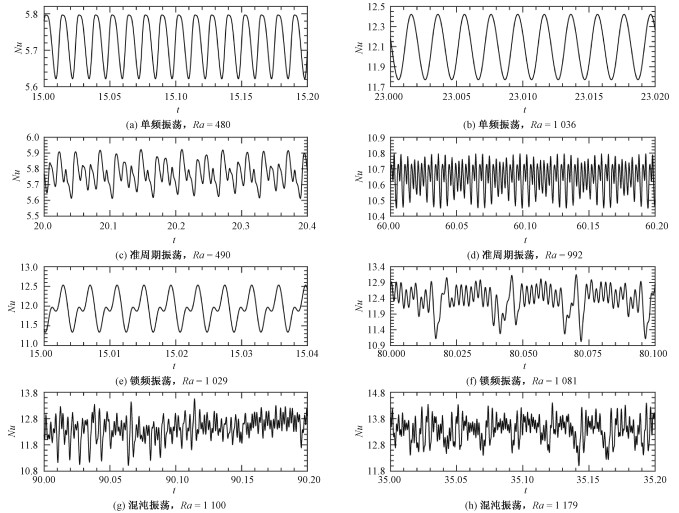
图 4~图 7分别用4种不同的作图方式对比单频、准周期、锁频和混沌振荡的特征,每种振荡类型各取2个示例。
|
Download:
|
| 图 4 不同Ra条件下,由计算Nu表征的无量纲热流作单频、准周期、锁频和混沌振荡的时间序列对比 Fig. 4 Time series comparison for single-frequency, quasiperiodic, frequency-locking, and chaotic oscillations in the calculated nondimensional heat flow represented by Nu at different Ra values | |
|
Download:
|
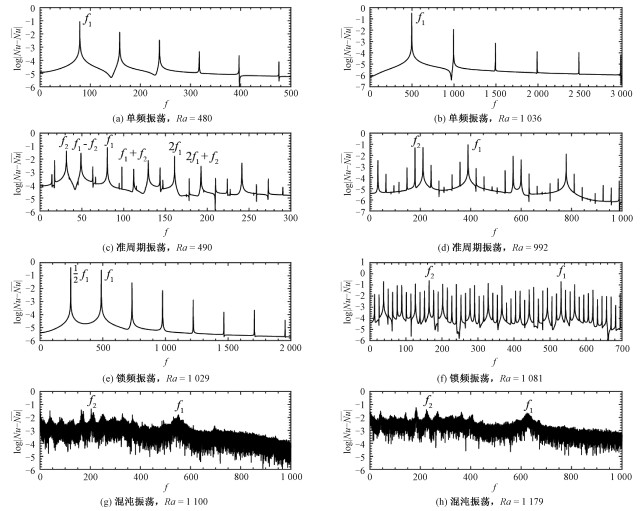
| 图 5 不同Ra条件下,由计算Nu表征的无量纲热流作单频、准周期、锁频和混沌振荡的功率谱对比 Fig. 5 Power spectrum comparison for single-frequency, quasiperiodic, frequency-locking, and chaotic oscillations in the calculated nondimensional heat flow represented by Nu at different Ra values | |
|
Download:
|
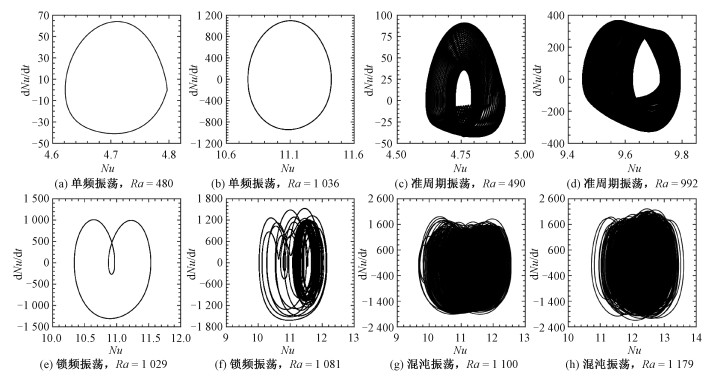
| 图 6 不同Ra条件下,由计算Nu表征的无量纲热流作单频、准周期、锁频和混沌振荡的相图对比 Fig. 6 Phase portrait comparison for single-frequency, quasiperiodic, frequency-locking, and chaotic oscillations in the calculated nondimensional heat flow represented by Nu at different Ra values | |
|
Download:
|
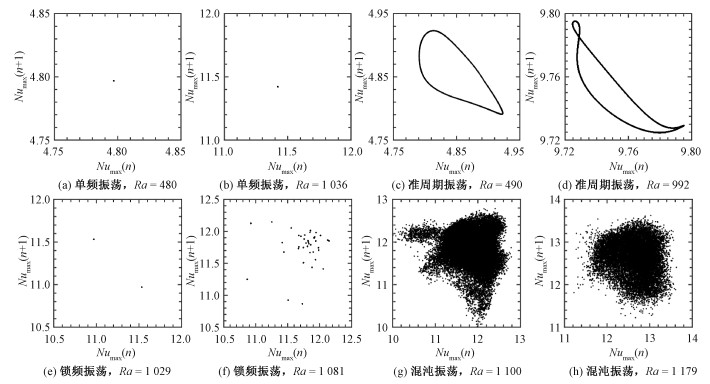
| 图 7 不同Ra条件下,由计算Nu表征的无量纲热流作单频、准周期、锁频和混沌振荡的洛伦兹映射对比 Fig. 7 Lorenz mapping comparison for single-frequency, quasiperiodic, frequency-locking, and chaotic oscillations in the calculated nondimensional heat flow represented by Nu at different Ra values | |
图 4以时间序列方式显示Nu的时间振荡。这种方式是计算结果的最原始形式的呈现,也是其他表示方法的基础。图 4(a)和4(b)分别表示P1和P5阶段的单频振荡,对应曲线均以周期型重复为特征,但每个周期内的振荡波形存在显著差异:图 4(a)的波峰与波谷形态非常不对称,而图 4(b)则高度对称。这是P1阶段混合模态对流与P5阶段中心对称对流在时间序列上的表现。图 4(c)和4(d)所示的准周期振荡曲线光滑但不存在周期性重复,与锁频振荡和混沌振荡各有相同与不同之处。分处L1和L2阶段的锁频振荡(图 4(e)和4(f)),是周期性重复的光滑曲线,但因包含成比例的不同频率而与单频振荡明显不同。图 4(g)和4(h)给出的混沌振荡时间序列曲线既无周期重复性又不光滑。
在时间序列曲线上光滑与否(甚至周期性重复与否)的直观特征很难准确量化,因而作为振荡类型区分的依据不够明确。从时间域变换到频率域,振荡行为包含的频率成分便可以一目了然。对应于图 4的8个示例,图 5给出了相应的功率频谱。在功率谱结果中,单频振荡(图 5(a)和5(b))只包含主频整数倍的频率成分。相对而言,图 5(b)中2倍主频的功率明显高于图 5(a),是前者峰谷对称而后者峰谷不对称的直接后果。对准周期振荡,图 5(c)和5(d)显示所有频谱成分都是2个不可公度基频的整系数线性组合。而在图 5(e)和5(f)所示的锁频振荡情形,2个基频比为有理数,频谱仅包含基频最大公约数的整数倍成分。在图 5(e)中主频之外的基频为主频的一半,而在图 5(f)中主频为最低频的42倍,而另一基频为最低频的13倍。所有单频、准周期和锁频振荡的功率谱都仅包含离散的频率成分,与图 5(g)和5(h)表示的混沌振荡近乎连续的频谱成分形成鲜明的对比。
严格来说,频谱离散与连续没有明确的界限,所以仅由功率谱识别混沌振荡并不完全可靠。相图和洛伦兹映射图能够为区分不同类型的振荡提供进一步的证据。
图 6给出了分别以Nu与其时间导数为横轴和纵轴表示的相图。相图中不包含时间或频率变量,所以周期性变化在相图上会体现为重复。图 6(a)和6(b)显示单频振荡表现为周而复始的极限环轨道。图 6(c)和6(d)所示的准周期振荡情形,由于基频不可公度,相空间轨迹在环面上无限往复。图 6(e)和6(f)所示的锁频振荡相图中,由于基频可公度,相空间轨迹分别在环绕2和42圈后首尾相接。图 6(g)和6(h)表示的混沌振荡,相空间轨迹则已不仅局限在环面上,而是将环内区域填满。
图 7利用洛伦兹映射[24]对相空间轨迹作降维显示。在图 4给出的时间序列中,每一次振荡必包含1个波峰,即1个Nu极大值。洛伦兹映射是以当前波峰值为横坐标、以下一个波峰值为纵坐标构成的二维序列。对单频振荡,由于所有的波峰都相等,而一次振荡仅取1个峰值,在洛伦兹映射下表现为横坐标等于纵坐标的1个孤立点,如图 7(a)和7(b)所示。在图 7(c)和7(d)所示的准周期振荡情形,由于一次振荡只取一个波峰值,二维环面上的轨迹就在洛伦兹映射图上降低一维,表现为连续的一维曲线。在图 7(e)和7(f)所示锁频振荡的洛伦兹映射图中,分别包含2和42个离散点,对应一个最低频相应的周期内分别包含2和42个波峰,以及相空间轨迹分别环绕2和42圈后首尾相接。而图 7(g)和7(h)表示的混沌振荡,经洛伦兹映射降维,仍然表现为充满区域的面状分布。
混沌振荡的相图和洛伦兹映射表示,还为揭示混沌吸引子的性质提供了指示。例如,导致蝴蝶效应的著名洛伦兹吸引子,在相图上表现为类似蝴蝶翅膀的优美形态,而洛伦兹映射图则集中在一条单峰曲线附近,均说明洛伦兹混沌吸引子非常薄,其分数维仅略高于2[24]。而图 6和图 7的混沌振荡结果则表明,方腔内孔隙自然对流中存在的混沌吸引子比洛伦兹吸引子分数维度更高、结构也更复杂。因为洛伦兹系统是对实际大气自然对流系统的高度简化,从无穷维简化为三维[24],而本文研究的自然对流问题是将无穷维实际系统截断简化成65×64维,其复杂性远远高于洛伦兹系统。
2.5 平均热流与振荡主频随Ra变化的定量关系传热学研究对工程应用最重要的指导意义是提供温差与热流间的定量关系。具体到自然对流问题,就是Nu随Ra变化的定量关系。此外,瞬态自然对流振荡主频随Ra的变化反映了热流振荡基本特征,也具有显著的工程意义。然而,对方腔内的孔隙自然对流问题,这些定量关系还没有建立。
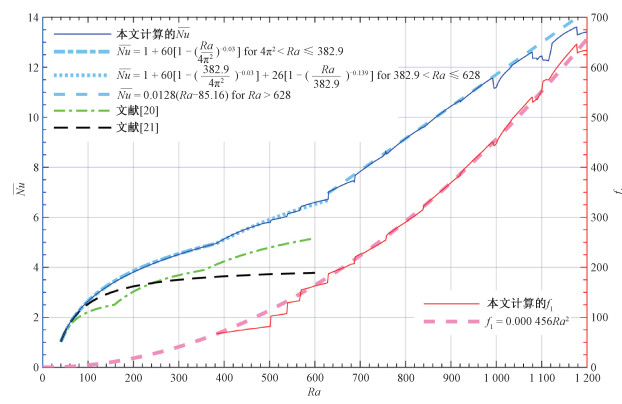
Graham和Steen[18]检验了热柱发育的高Ra对流情形,发现方腔内孔隙自然对流近似符合经典边界层分析给出的标度率[25]:Nu正比于Ra,而振荡主频正比于Ra2。具体结果是,在Ra介于700~925时,最小二乘拟合的计算Nu正比于Ra1.15,而振荡主频正比于Ra1.95,但没有提供拟合计算结果的解析公式。在稳态对流的初始阶段,孔隙对流方面的权威专著[5]引用了分别由Bories[20]和Palm等[21]给出的2个经验公式,但没有其适用Ra范围的论证。图 8将本文数值模拟得到的Nu与振荡主频单独从图 2(a)中提取出来,以方便与前人结果对比,并建立定量的拟合公式。
|
Download:
|
| 图 8 平均热流和振荡主频计算值与公式拟合值的对比 Fig. 8 Comparison between the calculated and formula-fitting values for the average heat flow and the primary oscillation frequency | |
图 8表明,Bories[20]和Palm等[21]给出的经验公式只在稳态对流发生后的很小一段Ra区间与本文计算的Nu符合良好。对更高的Ra值,2个经验公式的预测相差很大,且都明显低于本文计算值。另一方面,边界层分析给出的标度率,则在相当宽的Ra范围与本文结果符合良好。与Graham和Steen[18]的结果对比,本文结果不但符合边界层标度率的Ra区间更宽,而且符合的程度更高,以至于边界层标度率的幂次无需修改就可拟合本文结果。在热柱发育后的高Ra段存在几个局部偏离边界层标度率的小区间和Ra高于1 100以后的系统偏离,其成因可由Graham和Steen[18]详细论证的不同对流模态间的强相互作用和共振定性解释。
图 8同时提供了对本文Nu计算结果的三段拟合公式和对振荡主频结果的二次函数拟合公式。总体上,这些公式对计算结果的拟合较好,可以作为相应条件下实际工程设计和应用的便捷计算工具。
2.6 讨论本文基于达西定律数值模拟底部加热孔隙介质方腔内的二维自然对流,因此有必要对达西定律的适用性加以检验。前人研究表明,达西定律适用于雷诺数Re小于1的孔隙流动,而对更高雷诺数的孔隙流动,动量方程需要修正为非线性的Forchheimer方程[5]。对本文所研究的问题,雷诺数正比于无量纲达西速度,比例系数为孔隙介质等效热扩散率与渗透率平方根的乘积除以流体运动学黏度与渗流层厚度的乘积。由于本文所有计算结果得到的无量纲达西速度均小于500,而孔隙岩石的等效热扩散率与水、油气等流体的运动学黏度量级相当,本文数值模拟结果应用于渗透率以达西或毫达西计而自然对流层厚度以米或千米计的地球物理渗流问题,雷诺数均远小于1,因而达西定律完全适用,无需修正。
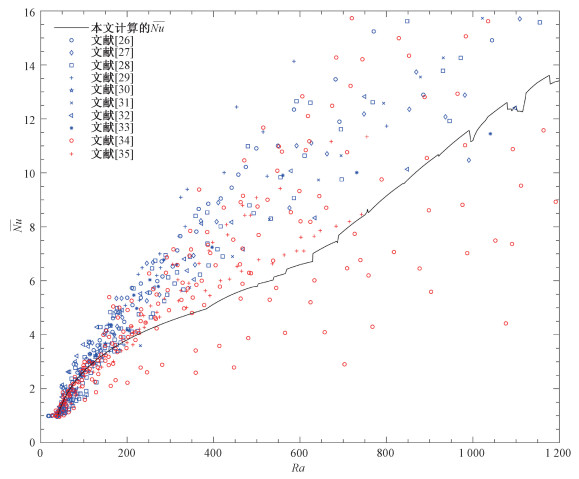
由于文献中描述方腔内孔隙自然对流的实验结果较少,本文模拟结果无法与方腔实验结果进行直接对比。然而,因为均匀水平孔隙层内最先发育的自然对流形态是宽度等于孔隙层厚度的二维对流环,等价于侧边界绝热的孔隙方腔内的二维自然对流,所以本文模拟结果可与水平孔隙层内的自然对流实验结果进行一定程度的对比。特别地,在Ra超过最小临界值4π2不太多的情况下,宽度等于孔隙层厚度的二维对流形态主导了水平层内的自然对流(从更高临界Ra开始发育的其他宽度-厚度比对流模态相对较弱),水平孔隙层内的自然对流实验结果应与本文数值结果接近。图 9给出了本文计算得到的平均热流随Ra变化曲线与底部加热水平孔隙层内自然对流已有实验结果[26-35]的对比。图 9表明,Ra小于200的大多数实验结果与本文数值结果一致,而在更高的Ra条件下,实验结果越来越分散。考虑到图 9中实验数据来自于多种不同的宽度-厚度比实验装置,在高Ra条件下,自然对流受多个不同宽度-厚度比模态的复杂叠加控制,实验结果分散的趋势在定性意义上是可以理解的。此外,在高Ra情况下,基于达西定律的数值模拟结果与多数实验数据存在显著偏离的趋势,则可以由实验条件已不能满足雷诺数小于1的达西定律成立条件来解释。
|
Download:
|
| 图 9 平均热流随Ra变化计算结果与实验结果的对比 Fig. 9 Comparison between the calculated and experimental results for the average heat flow varying with Rayleigh number | |
本文结果的应用主要针对地球物理渗流与传热问题。采用的侧面绝热方腔模型是实际方腔内自然对流和水平横向尺度远大于垂向对流层厚度的水平层内自然对流的理想近似。对于方腔自然对流问题,由于对流具有远高于热传导的传热效率,设定侧面边界绝热而忽略方腔之外围岩向方腔内的热传导效应是一个合理的近似。事实上,这样的边界条件设定被数值模拟地球物理渗流与传热问题的前人研究普遍采用,其合理性也由地热储层与围岩耦合传热的数值模拟研究[36]直接证实。对于水平层内自然对流问题,侧面绝热则是多个对流环满足周期对称性的必然要求。
3 结论本文对底部加热孔隙介质方腔内二维自然对流进行的模态完备的数值模拟研究,得到了Ra单调递增情形下自然对流动力学演化的完整路径,包括21个不同演化阶段。自然对流的空间形态是其组成模态及对称性的反映,而对流形态的空间变化受到行波波数由4到14顺序递增与热柱发育程度的共同控制。自然对流随时间振荡的不同类型(单频、准周期、锁频和混沌)表现为时间序列图、功率谱图、相图与洛伦兹映射图上的显著不同特征。几种作图方式相结合,能够更准确地区别不同振荡类型,包括揭示混沌吸引子的复杂形态。计算得到的平均热流及其振荡主频可由简单解析公式较好地拟合,并在很宽的Ra范围内与经典边界层标度率一致。
| [1] |
Horton C W, Rogers F T Jr. Convection currents in a porous medium[J]. Journal of Applied Physics, 1945, 16(6): 367-370. Doi:10.1063/1.1707601 |
| [2] |
Lapwood E R. Convection of a fluid in a porous medium[J]. Mathematical Proceedings of the Cambridge Philosophical Society, 1948, 44(4): 508-521. Doi:10.1017/S030500410002452X |
| [3] |
孔祥言. 高等渗流力学[M]. 合肥: 中国科学技术大学出版社, 1999.
|
| [4] |
Phillips O M. Geological fluid dynamics: sub-surface flow and reactions[M]. Cambridge, UK: Cambridge University Press, 2009. Doi:10.1017/cbo9780511807473
|
| [5] |
Nield D A, Bejan A. Convection in porous media[M]. 5th ed. Cham: Springer International Publishing, 2017. Doi:10.1007/978-3-319-49562-0
|
| [6] |
Neufeld J A, Hesse M A, Riaz A, et al. Convective dissolution of carbon dioxide in saline aquifers[J]. Geophysical Research Letters, 2010, 37(22): L22404. Doi:10.1029/2010GL044728 |
| [7] |
Akhbari D, Hesse M A. Causes of underpressure in natural CO2 reservoirs and implications for geological storage[J]. Geology, 2017, 45(1): 47-50. Doi:10.1130/G38362.1 |
| [8] |
Huang X X, Zhu J L, Li J, et al. Fluid friction and heat transfer through a single rough fracture in granitic rock under confining pressure[J]. International Communications in Heat and Mass Transfer, 2016, 75: 78-85. Doi:10.1016/j.icheatmasstransfer.2016.03.027 |
| [9] |
Wen B L, Corson L T, Chini G P. Structure and stability of steady porous medium convection at large Rayleigh number[J]. Journal of Fluid Mechanics, 2015, 772: 197-224. Doi:10.1017/jfm.2015.205 |
| [10] |
孔祥言, 卢德唐, 徐献芝, 等. 多孔介质中对流的研究[J]. 力学进展, 1996, 26(4): 510-520. Doi:10.6052/1000-0992-1996-4-J1996-048 |
| [11] |
Kimura S, Schubert G, Straus J M. Route to chaos in porous-medium thermal convection[J]. Journal of Fluid Mechanics, 1986, 166: 305-324. Doi:10.1017/S0022112086000162 |
| [12] |
Schubert G, Straus J M. Transitions in time-dependent thermal convection in fluid-saturated porous media[J]. Journal of Fluid Mechanics, 1982, 121: 301-313. Doi:10.1017/S0022112082001918 |
| [13] |
Kimura S, Schubert G, Straus J M. Instabilities of steady, periodic, and quasi-periodic modes of convection in porous media[J]. Journal of Heat Transfer, 1987, 109(2): 350-355. Doi:10.1115/1.3248087 |
| [14] |
Steen P H, Aidun C K. Time-periodic convection in porous media: transition mechanism[J]. Journal of Fluid Mechanics, 1988, 196: 263-290. Doi:10.1017/S0022112088002708 |
| [15] |
Graham M D, Steen P H. Strongly interacting travelling waves and quasiperiodic dynamics in porous medium convection[J]. Physica D: Nonlinear Phenomena, 1992, 54(4): 331-350. Doi:10.1016/0167-2789(92)90042-L |
| [16] |
de la Torre Juárez M, Busse F H. Stability of two-dimensional convection in a fluid-saturated porous medium[J]. Journal of Fluid Mechanics, 1995, 292: 305-323. Doi:10.1017/S0022112095001534 |
| [17] |
Aidun C K, Steen P H. Transition to oscillatory convective heat transfer in a fluid-saturated porous medium[J]. Journal of Thermophysics and Heat Transfer, 1987, 1(3): 268-273. Doi:10.2514/3.38 |
| [18] |
Graham M D, Steen P H. Plume formation and resonant bifurcations in porous-media convection[J]. Journal of Fluid Mechanics, 1994, 272: 67-90. Doi:10.1017/S0022112094004386 |
| [19] |
Horne R N, Caltagirone J P. On the evolution of thermal disturbances during natural convection in a porous medium[J]. Journal of Fluid Mechanics, 1980, 100(2): 385-395. Doi:10.1017/S0022112080001218 |
| [20] |
Bories S. Natural convection in porous media[M]//Bear J, Corapcioglu M Y. Advances in Transport Phenomena in Porous Media. Dordrecht: Springer Netherlands, 1987: 77-141. DOI: 10.1007/978-94-009-3625-6_4.
|
| [21] |
Palm E, Weber J E, Kvernvold O. On steady convection in a porous medium[J]. Journal of Fluid Mechanics, 1972, 54(1): 153-161. Doi:10.1017/S002211207200059X |
| [22] |
Orszag S A. Numerical simulation of incompressible flows within simple boundaries. I. Galerkin (spectral) representations[J]. Studies in Applied Mathematics, 1971, 50(4): 293-327. Doi:10.1002/sapm1971504293 |
| [23] |
Ferziger J H, Peric'M. Computational methods for fluid dynamics. 3rd ed[M]. Berlin, Heidelberg: Springer Berlin Heidelberg, 2002. Doi:10.1007/978-3-642-56026-2
|
| [24] |
Strogatz S. Nonlinear dynamics and chaos: with applications to physics, biology, chemistry, and engineering[M]. 2nd ed. Boca Raton: CRC Press, 2018.
|
| [25] |
Howard L N. Convection at high Rayleigh number[M]//Görtler H. Applied Mechanics. Berlin, Heidelberg: Springer Berlin Heidelberg, 1966: 1109-1115. DOI: 10.1007/978-3-662-29364-5_147.
|
| [26] |
Buretta R J, Berman A S. Convective heat transfer in a liquid saturated porous layer[J]. Journal of Applied Mechanics, 1976, 43(2): 249-253. Doi:10.1115/1.3423818 |
| [27] |
Close D J, Peck M K. Experimental determination of the behaviour of wet porous beds in which natural convection occurs[J]. International Journal of Heat and Mass Transfer, 1986, 29(10): 1531-1541. Doi:10.1016/0017-9310(86)90068-2 |
| [28] |
Combarnous M A, Bories S A. Hydrothermal convection in saturated porous media[M]//Chow V T. Advances in Hydroscience. Amsterdam: Elsevier, 1975: 231-307. DOI: 10.1016/B978-0-12-021810-3.50008-4.
|
| [29] |
Elder J W. Steady free convection in a porous medium heated from below[J]. Journal of Fluid Mechanics, 1967, 27(1): 29-48. Doi:10.1017/S0022112067000023 |
| [30] |
Kaneko T, Mohtadi M F, Aziz K. An experimental study of natural convection in inclined porous media[J]. International Journal of Heat and Mass Transfer, 1974, 17(4): 485-496. Doi:10.1016/0017-9310(74)90025-8 |
| [31] |
Kazmierczak M, Muley A. Steady and transient natural convection experiments in a horizontal porous layer: the effects of a thin top fluid layer and oscillating bottom wall temperature[J]. International Journal of Heat and Fluid Flow, 1994, 15(1): 30-41. Doi:10.1016/0142-727X(94)90028-0 |
| [32] |
Lister C R B. An explanation for the multivalued heat transport found experimentally for convection in a porous medium[J]. Journal of Fluid Mechanics, 1990, 214: 287-320. Doi:10.1017/S0022112090000143 |
| [33] |
Schneider K J. Investigation of the influence of free thermal convection on heat transfer through granular material[M]//Proceedings of the XIth International Congress of Refrigeration. Progress in refrigeration science and technology. Amsterdam: Elsevier, 1965: 247-254. DOI: 10.1016/b978-1-4831-9857-6.50053-4.
|
| [34] |
Seki N, Fukusako S, Ariake Y. Experimental study of free convective heat transfer in a liquid-saturated porous bed at high Rayleigh number[J]. Wärme und Stoffübertragung, 1980, 13(1): 61-71. Doi:10.1007/BF00997634 |
| [35] |
Yen Y C. Effects of density inversion on free convective heat transfer in porous layer heated from below[J]. International Journal of Heat and Mass Transfer, 1974, 17(11): 1349-1356. Doi:10.1016/0017-9310(74)90136-7 |
| [36] |
丁军锋, 王世民. 增强型地热系统的多区域多物理场耦合三维数值模拟[J]. 中国科学院大学学报, 2019, 36(5): 694-701. Doi:10.7523/j.issn.2095-6134.2019.05.015 |
 2024, Vol. 41
2024, Vol. 41 


