现实生活中有很多决策问题,如商铺选址和公交地铁系统设计站点等,需要考虑很多影响因素之间的互相关联和限制的问题。这类选择问题的共同处在于可选项是有限的,而最后决策的优劣性的评估标准也是有限的。通过这些评估标准比较各个选择,能够得到最优选,其次可以从整体上得到各个选择的评级和分类。这类对多种标准的决策问题进行评价定级、分类的行为称作多标准决策分析(decision analysis by multiple criteria,MCDA)。MCDA的选择及其评估标准是有限的,这些评估标准可以是有序数字,那么分析后将获得不同选择的评级和排序;评估标准也可以是基础数值,即选择被量化后的具体值。通过累计这些基数或序数的标准,并考虑决策者们(decision makers,DM)对不同标准的重视和偏好程度,对每一个选择作出整体性的评估,是MCDA的最终目的。由此可见,MCDA不仅依靠对标准值的量化规则,还依靠不同决策者主观上的偏好,以及评估中用到的模型和模型中的各项设定参数。如果可以通过各种MCDA方法对决策问题进行分析以获得决策建议,那么将这些方法应用于决策是有用的。因此,决策者需要熟悉使用各种多准则决策分析技术的先决条件以及灵活应用不同方法的优缺点。
MCDA研究是一个较新的领域,很多方法仅用于处理实际生活中某些特定领域的特定多目标决策问题,大致分为两类。一类是Keeney等[1]发展出的多属性效用方法(multiattribute utility theory,MAUT),是广泛应用至今的主要方法之一,而另一大类被广泛采用的多标准决策分析方法是高分法(outranking methods),如Roy[2]提出的ELECTRE方法,Brans和Mareschal[3]提出的PROMETHEE方法,以及Xu[4]给出的SIR方法等。MAUT理论的构建为当今MCDA的发展打下了根基,相对于高分法,其应用了更多相对复杂的数学模型;而高分法,比如ELECTRE方法,能够从更多不同的角度对偏好信息建模,也具有一定优势。这两类方法都得到了广大决策者的青睐和应用。
MAUT基于效用函数,是目前MCDA中应用时间最长的方法,并广受好评。这类方法首先建立效用函数,然后根据标准的值得出效用评分,最后根据得出的效用评分评估不同选择的优劣。近年来,效用函数方法广泛应用,但同时也出现了越来越多无法得到模型所需具体参数的情况,例如,决策者不愿意透露其偏好信息,导致缺少必要的建模参数,或是评估这些选择的各个标准的值本身就是不确定或者不准确的。原始的MAUT和高分法在这一方面皆有不足,因此,应对模型参数的不确定性或不准确性,需要对以往的效用理论方法进行改进。逆向推断进行决策分析是一个可行的改进思路,也就是说,与其去咨询或寻找具体决策问题所用模型中的具体参数,不如反过来考虑每一种决策结果是由哪些具体参数所决定。于是,随机多标准可接受度分析(stochastic multi-criteria acceptability analysis,SMAA)方法应运而生并在近些年飞速发展。它就是这样一种逆向分析的方法,允许标准值和偏好信息的不确定性,从而解决了很多其他方法所遇到的困难。
不同的SMAA方法可以用来处理多标准决策中的主要3种情形:选优、评级和分类。这类方法包含了一系列多标准决策方法,其优势在于扩展了决策分析的角度,即反向分析所有可能的参数空间中的取值,并且允许标准值和偏好信息的缺失,甚至在没有任何偏好信息的极端情况下也可以使用。这里所说的标准值和偏好信息的缺失包含3种可能的情形,即不完整、不准确和不确定。不完整意味着部分信息未获得,不准确意味着信息虽获得但准确性不足,不确定意味着虽然决策问题的相关观察者给出了他们完整且准确的信息,但这些信息并不可靠。偏好信息可量化为不同标准所占的权重,SMAA方法基于探索权重向量空间来得到使每个备选方案成为最优方案的偏好信息,或者为特定选择方案提供其取得不同评级的概率。例如,相比于给出一个整体评级,SMAA-2方法提供了各个选择取得特定评级的概率。
Lahdelma等[5]首次提出SMAA方法。Lahdelma和Salminen[6]将秩可接受度的概念引入SMAA方法中,发展出SMAA-2方法。该方法分析得到的主要结果是秩可接受度指数、中心权重向量以及在中心权重向量下的置信因子。秩可接受度指数描述了使得选择方案位于特定等级(秩)的不同偏好的所占比例,中心权重向量表示使每个选择成为最优的偏好的典型代表,而置信因子衡量这些秩可接受度是否足够可信,从而做出明智的决定。Lahdelma等[7]将SMAA方法进一步扩展,发展出SMAA-O方法,这一方法将序数作为标准值,即决策者对每一项标准进行评级并得到序数,再进行SMAA分析。上述几种SMAA方法都是针对选择或评级之类的决策问题,而Yu[8]提出的ELECTRE TRI方法是一类针对分类问题的决策方法,在现实生活中有广泛的应用,Tervonen等[9]将其扩展为SMAA-TRI方法,其目的在于允许参数的缺失和不确定,并研究ELECTRE TRI方法分析结果的稳健性,其分析结果展现了哪些参数取值将一种选择归为特定的分类中。Tervonen等[10]还将类似的扩展应用到另一类常用的评级方法——ELECTRE Ⅲ方法中,给出了SMAA-Ⅲ方法,同样解决了参数不确定或不准确所带来的难题,并且可以很方便地进行稳健性分析。数据包络分析(data envelopment analysis, DEA)也是基于效用理论的多标准决策方法,它将不同的选择判定为有效的或无效的选择,和SMAA类似,它也用一个总效用函数来描述每一种选择,其中几个标准的不同重要性则由权重来体现。Lahdelma和Salminen[11]考虑到将DEA和SMAA-2方法结合使用,提出SMAA-D方法,它可被视为是将DEA类型的效用函数应用到SMAA-2中,用来提供随机的有效性的度量。前景理论(prospect theory)是经济学研究中广泛应用的思想,但很少被应用到决策分析中,Lahdelma和Salminen[12]首次将前景理论和SMAA方法相结合,提出了SMAA-P方法,该方法以前景理论所认为的损失重于得到的观点为出发点进行SMAA分析。由此可见,SMAA方法的核心思想可以与以往的各类多标准决策方法相结合。除上述这些方法外,Corrente等[13]提出的SMAA-PROMETHEE方法,则是将SMAA与另一种常用的多标准决策方法——PROMETHEE方法相结合,进而探索与决策者提供的某些偏好信息一致相容的所有权重。根据应用场景的不同,SMAA方法会涉及不同的关于概率分布的积分,并且可能非常复杂。通常,积分也具有很高维数。基于离散化每个维度分布的数值积分方法是不可行的,因为所需的计算量取决于维数。因此,相比于尝试获得积分的精确值,应用蒙特卡罗模拟来获得足够准确的近似值成为了常用的手段。Tervonen和Lahdelma[14]给出了有关模拟算法的完整说明,并研究了计算的准确性以及复杂性问题。
多种多样的SMAA方法已经在各种现实生活中的决策问题中有所应用,Hokkanen等[15]研究如何确定总体计划的实施顺序的问题,并且解决了港口引证的问题[16],还研究了选择污染土壤的清除剂的决策[17];Lahdelma等[18]研究废物处理设施引证的问题;Tervonen等[19]设计了电梯规划方案,还曾设计了溢油应急响应框架[9];Kangas等[20]给出了森林规划的决策建议。在国内近些年的研究中,SMAA方法也在各个领域发挥出了作用。Xia等[21]用SMAA方法为物流服务供应商提供了针对物流配送中心的选址方面的建议;Zhu等[22]研究了水库洪水防治的操作策略。
改革开放后中国经济飞速发展,时局瞬息万变,决策者们在营销策划、产品更替、项目投资等等领域中,面临选择时需要考虑越来越多的因素和标准,而这些决策因素和标准相互之间联系紧密,在数据结构上存在着复杂的相依关系,在应用SMAA方法研究这些问题时,可以通过概率分布来表示部分或全部缺失的偏好信息以及标准值的不确定性,然而这些相依性则很难被准确地量化。尽管SMAA方法已经发展成熟,出现了很多形式和变化,但现有方法大都不能很有效地对这些相依结构的信息进行量化和分析。Lahdelma等[23]提出用独立分布来处理高维数据是不合理的,必须要充分考虑这些变量之间相依性的信息,考虑到高斯分布被广泛应用到各个领域,他们首次提出将高斯分布(多元正态模型)运用到SMAA方法中。虽然独立分布并不可取,但是,文献[23]并未充分论述采用高斯分布的合理性。实际上,高斯分布局限于变量之间是线性的相依关系的情形,对于非线性结构,就不太准确和适用。弥补这方面不足是本文研究的出发点。考虑到copula函数是分析变量间相依关系最有利的工具,擅长处理多元变量间各种类型的相依关系,已经在金融市场、风险传递等领域广泛应用,因而本文从这一点出发,将copula相依分析与SMAA方法首创性地相结合来改善以往的SMAA方法。一些copula理论研究的前沿文献为本文提供了相应的理论基础。Genest等[24-25]总结了关于二元copula函数的拟合优度检验和参数估计的方法。以Joe[26]提出的关于给定边际分布的多元分布函数的构造理论为基础,Bedford和Cooke[27]提出了藤结构的概念,通过pair-copula模型,首次解决了多维变量之间相依关系的问题。Aas等[28]首次用统计方法推断出藤copula的计算公式。相比较C族藤和D族藤的copula函数,R藤copula有着更加灵活多样的相依结构。随着相关研究的进展,R藤模型越来越多地应用于各个领域,来处理多维变量的相依结构。
本文首先对SMAA-2的方法进行回顾,介绍R藤结构的构造算法和copula函数的拟合方法,总结SMAA-2和R藤copula方法相结合的应用步骤。然后进行模拟试验分析,模拟出一万个样本,这些样本都是包含2个评估标准和3个选择方案的6维决策变量。应用藤copula拟合方法,拟合出6维决策变量的联合概率分布,来量化其相依结构和不确定性,并结合使用SMAA-2方法,根据联合概率分布计算出备选方案的各等级的秩可接受度。最后,在两种不同相依结构的决策变量下,分别对采用多元正态模型处理相依关系的方法以及本文提出的新方法进行对比分析,比较出在不同情况下,这些方法是否能够适用,以及它们各自的优缺点。
1 SMAA基础理论SMAA是一种多标准决策方法。在应用SMAA方法时,决策者不需要将他们的偏好信息明确地表达出来,相反,基于对权重空间的探索,该方法可以描述出每个备选方案担任最优解的概率以及计算的可靠性。决策变量的不确定或不准确的值由概率分布来表示。本文应用到的SMAA-2方法,通过计算各个选择的所有排序的接受度,也称为秩可接受度,综合地判断每个选择的优劣,最早由Lahdelma和Salminen[6]提出该方法。
SMAA-2应用对权重空间分析和划分来描述每种选择方案,即将总权重空间划分为使某种选择成为最优选择的子权重空间,以及将其置于其他各个等级的子权重空间。一般地,决策问题表示为一组m个选择{x1, x2, …, xm}根据n个标准进行评估,其评估的优劣用各自定义的效用函数来表示,进而研究如何使得加权后总效用最优。权重向量即代表了DM的偏好结构,第i个选择的加权效用由实值效用函数u(xi, w)表示。这个总效用函数通过使用权重向量w来量化DM的主观偏好,从而将不同的选择方案映射到一个实际的值。SMAA-2方法适用于决策变量和权重均未精确了解的情况。不确定的决策变量由随机变量ξij表示,它是空间
| $ W{\rm{ }} = \{ w \in {\mathbb{R}^n}:{w_j} \ge {\rm{ }}0, \sum\limits_{j{\rm{ }} = 1}^n {{w_j}} = 1\}. $ | (1) |
效用函数用于将随机决策变量和权重分布映射到效用分布u(ξi, w)。基于效用分布,可以通过排序函数定义每个选择的等级,其取值从最佳等级(1)到最差等级(m):
| $ {\rm{rank}}(i,\mathit{\boldsymbol{\xi }},\mathit{\boldsymbol{w}}) = 1 + \sum\limits_{k = 1}^m {\rho (u(\mathit{\boldsymbol{\xi }}k,\mathit{\boldsymbol{w}})} > u(\mathit{\boldsymbol{\xi }}i,\mathit{\boldsymbol{w}})) $ | (2) |
其中:ρ(true)=1, ρ(false)=0。SMAA-2是以分析最优等级(秩)的随机权重集合为基础的,其秩为r的随机权重子空间定义为
| $ W_i^r(\mathit{\boldsymbol{\xi }}) = \{ \mathit{\boldsymbol{w}} \in W:{\rm{rank}}(i,\mathit{\boldsymbol{\xi }},\mathit{\boldsymbol{w}}) = r\} $ | (3) |
这个Wir权重空间里的任意权重都使选择xi的被排在第r个等级。
SMAA-2的第一个描述性指标是秩可接受度bir,其计算方法为
| $ b_i^r = {\smallint _{\mathit{\boldsymbol{\xi }} \in X}}{f_X}(\mathit{\boldsymbol{\xi }}){\smallint _{\mathit{\boldsymbol{w}} \in W_i^1}}{f_W}(\mathit{\boldsymbol{w}}){\rm{d}}\mathit{\boldsymbol{w}}{\rm{d}}\mathit{\boldsymbol{\xi }} ,$ | (4) |
式中对w的积分表示Wir权重空间占总权重空间的比例,之后对ξ进行积分得到它的期望值,直观地理解也就是使选择xi排序为r的权重空间占总权重空间的比例的期望值。秩可接受度可以直接用于多标准选择的评估,当秩取r=1时,简称为可接受度,记为ai。一般地,认为可接受度越大,那么对应的选择越可靠。然而在一些特殊情况下,例如存在两种非常相近的选择时,它们各自的可接受度会被彼此“剥削”而各得一半,使得每个可接受度都不高,因此仅仅考虑可接受度ai是不够的,对于这些特殊情况,将bir考虑进来,综合考虑使得每种选择排序靠前的可能性,将得到更好的分析结果,这也是SMAA-2方法相比于SMAA方法所改进的地方。对于大样本问题,Lahdelma和Salminen[6]建议用迭代的形式,定义其k最佳迭代秩可接受度为
| $ a_i^k{\rm{ }} = \sum\limits_{r = 1}^n {b_{{i^.}}^r} $ | (5) |
在用秩可接受度来比较选择方案的优劣性时,除了直接比较上式中air(r的值由决策者选择)的大小,还可以采用一种互补的方法,对秩可接受度求加权和,从而得到每个选择的整体可接受性指数aih,即
| $ a_i^h{\rm{ }} = \sum\limits_r^{} {{\alpha ^r}b_{{i^.}}^r} $ | (6) |
这里,如何选择每个秩的权重,也需要有所考量,通常排在前面的权重应大于秩靠后的权重。
中心权重向量wic是使得选择方案成为最优选择的权重向量空间的期望重心(质心)。中心权重向量表示支持此决策方案的决策者的“典型”偏好。可以向决策者呈现不同选择方案的中心权重,以帮助他们理解不同权重如何与决策分析结果的不同最优选择相对应。中心权重向量wic在数值上的计算公式如下
| $ \mathit{\boldsymbol{w}}_\mathit{\boldsymbol{i}}^\mathit{\boldsymbol{c}} = {\smallint _{\mathit{\boldsymbol{\xi }} \in X}}{f_X}(\mathit{\boldsymbol{\xi }}){\smallint _{w \in W_i^1}}{f_W}(\mathit{\boldsymbol{w}})\mathit{\boldsymbol{w}}{\rm{d}}\mathit{\boldsymbol{w}}{\rm{d}}\mathit{\boldsymbol{\xi }}/b_i^1. $ | (7) |
置信因子pic是当使用代表某个选择的中心权重向量作为偏好信息时,该选择确实成为最优选择的概率。置信因子计算公式如下
| $ p_i^c = {\smallint _{\mathit{\boldsymbol{\xi }} \in X:{\rm{rank}}(i,\mathit{\boldsymbol{\xi }},\mathit{\boldsymbol{w}}) = 1}}{f_X}(\mathit{\boldsymbol{\xi }}){\rm{d}}\mathit{\boldsymbol{\xi }}. $ | (8) |
事实上,对于任何给定的权重向量,都可以类似地计算置信因子。置信因子可以衡量秩可接受度能否足够准确地辨别选择方案是否有效。如果一个选择的可接受度很高,但置信因子较低的话,那么则需要综合考虑其各个秩可接受度再做分析。相反的,如果一个选择可接受度非常低,而置信因子又非常高的话,那么则有充分的理由排除这个选择。
2 藤copula方法 2.1 多元copula的PCC构造copula函数是研究随机变量间相依关系的有力工具,通过它可以将边缘分布和变量间的相依结构分开处理。copula的概念最早由Sklar[29]提出,它用来描述多维分布函数和低维边缘分布之间的关系。Sklar给出的定理成为这一领域理论研究的基础,也是概率空间理论中的重要定理之一。为方便后文的理解,这里将Sklar定理复述如下:
定理2.1
令F为联合分布函数,且边缘分布为F1, …, Fn,则存在copula函数C: [0, 1]n→[0, 1],使得对所有
由copula函数可定义联合分布的密度函数如下
| $ f({x_1}, \ldots {x_n}) = {\rm{ }}{c_{12 \ldots n}}({F_1}({x_1}), \ldots , {F_n}({x_n}))\prod\limits_{i = 1}^n {{f_n}({x_i})} ,$ | (9) |
其中
构造高维情形下的copula通常是件很困难的事情。已有的具有显示表达式的多参数多元copula函数并不多样,并且特定的函数形式未必能够很好地拟合现实生活中的数据。以Joe[26]的方法为基础,Bedford和Cooke[27]给出一种能灵活地利用二元copula函数构造高维联合分布的方法,将高维数据的处理转化为对多组二元数据的处理。而对于用copula函数拟合二元数据,则有相当完备的方法,大致分为3步:第一是对模型参数的估计,第二是对估计结果进行假设检验,第三是对不同的备选模型进行比较。
对模型参数的估计通常采用秩相关系数[30],或者采用极大似然法。其对数似然函数可以表示为
| $ l(\mathit{\boldsymbol{\theta }}) = \sum\nolimits_{i = 1}^n {log{c_\mathit{\boldsymbol{\theta }}}} (F({X_i}),G({Y_i})),$ | (10) |
其中cθ是copula密度函数,这里的极大似然性是对式(10)中全部参数计算的,包括边缘分布F, G的未知参数。在实际应用中,为简化运算,可以利用经验分布来代替边缘分布,经验分布采用如下形式
| $ {F_n}(x) = \frac{1}{{n + 1}}\sum _{i = 1}^n{\rm{II}}({X_i} \le x){\rm{ }},$ |
| $ {G_n}(x) = \frac{1}{{n + 1}}\sum _{i = 1}^n{\rm{II}}({Y_i} \le y){\rm{ }},$ |
其中采用n+1是为了保证分布函数值在区间[0, 1)内部,II是示性函数,当括号内不等式成立时取1,否则取0。用(Fn(Xi), Gn(Yi))替代似然函数(10)中的F(Xi), G(Yi),再对其最大化计算出极大似然估计,省去了对边缘分布的参数估计,这也称为伪似然法。
对于模型的假设检验,通常采用一类goodness-of-fitting检验方法,它们可以用来拒绝不好的拟合模型,已经被广泛应用于各类统计研究中。在采用多种参数型copula和多种参数估计的方法得到备选二元copula函数模型后,需要进行比较,选取拟合结果最好的作为最终模型。AIC准则(Akaike information criterion)是使用最为广泛的对模型进行选择的方法,对于二元copula的建模,其AIC定义为
| $ {\rm{AIC}} = {\rm{ }} - 2\sum\limits_{i{\rm{ }} = 1}^n {} {\rm{ln}}[{c_\theta }({U_{{i}{\rm{1}}}}, {U_{{i}2}})] + 2k. $ | (11) |
根据AIC准则将选取AIC最小的模型作为最优模型。
以二元copula为基础,可将多元随机变量转换为多个二元copula函数的乘积形式,进而用二元的方法来处理高维情形的问题。对于多元随机变量,其联合密度函数可以分解为条件边缘密度的乘积的形式
| $ f({x_1}, \ldots {x_n}) = {\rm{ }}f({x_1})\cdot f({x_2}|{\rm{ }}{x_1})\cdot f({x_3}|{\rm{ }}{x_1}, {x_2}) \ldots\begin{array}{*{20}{l}}\cdot {f({x_n}|{\rm{ }}{x_1}, \ldots {x_{n - 1}}), } \end{array} $ | (12) |
其中等式右边的第2项可改写为
| $ \begin{array}{*{20}{l}} {({x_2}|{\rm{ }}{x_1}) = } \end{array}\frac{{\begin{array}{*{20}{l}} {f({x_1}, {x_2})} \end{array}}}{{f({x_1})}}\begin{array}{*{20}{l}} { = {\rm{ }}c({F_1}({x_1}), {F_2}({x_2}))\cdot f({x_2})} \end{array}. $ |
类似地,式(12)中等号右边的第3项可以展开为
| $ \begin{array}{c} f({x_3}|{\rm{ }}{x_1}, {x_2}) = \frac{{\begin{array}{*{20}{l}} {f({x_1}, {x_2}, {x_3})} \end{array}}}{{f({x_1}, {x_2})}} = \frac{{f({x_2}, {x_3}|{\rm{ }}{x_1})f({x_2}|{\rm{ }}{x_1})}}{{f({x_2}|{\rm{ }}{x_1})}}\\ = {\rm{ }}{c_{23|1}}({F_{2|1}}({x_2}|{\rm{ }}{x_1}), {F_{3|1}}({x_3}|{\rm{ }}{x_1}))\cdot f(x3|{\rm{ }}x1)\cdot\\ f({x_3}|{\rm{ }}{x_1}) = \frac{{f({x_1}, {x_3}|{\rm{ }}{x_2})}}{{f({x_1}|{\rm{ }}{x_2})}}\\ = {\rm{ }}{c_{13|2}}({F_{1|2}}({x_1}|{\rm{ }}{x_2}), {F_{3|2}}({x_3}|{\rm{ }}{x_2}))\cdot f({x_3}|{\rm{ }}{x_2}) \end{array}. $ |
其中c23 |1和c13 |2分别表示连接条件分布F2 |1和F3 |1,以及连接条件分布F1 |2和F3 |2的copula函数的密度。一般地,关于条件密度的分解有下述公式
| $ f({x_i}\mathit{\boldsymbol{v}}) = {c_{{x_i},{x_j}|{\mathit{\boldsymbol{v}}_{ - j}}}}(F({x_i}|{\mathit{\boldsymbol{v}}_{ - j}}),F({x_j}|{\mathit{\boldsymbol{v}}_{ - j}})) \cdot f({x_i}|{\mathit{\boldsymbol{v}}_{ - j}}),$ | (13) |
其中:i, j=1, 2, …, n;v是集合{x1, x2, …, xn}的任意子集且包含xj但不包含xi;而v- j即表示从v中除去xj所得的集合。不难看出,利用式(13)将式(12)中的条件密度每做一次分解,将产生一个新copula密度,而条件集的元素则减少一个。不断地重复这样的分解步骤,即可将联合密度f(x1, …, xn)展开为两部分,一部分为边缘密度的乘积,即
通过构建PCC可以看出,对于多元随机变量的建模问题被分解为对一系列二元相依关系的建模。例如对c12的拟合,只需考虑如何构造出边缘分布F1(X1)和F2(X2)的copula函数,而这只需获取X1和X2的一列独立样本,即可采用多种多样的方法去实现很好的拟合。进一步,还可以很好地拟合c23|1,这只需考虑构造出条件分布F2|1和F3|1的copula函数,但这一步的样本数据由上一步中的copula函数转换而来,将用到如下公式
| $ F(x{\rm{ }}|\mathit{\boldsymbol{v}}) = \frac{{\partial {C_{x\mathit{\boldsymbol{v}}}}(F(x), F(\mathit{\boldsymbol{v}}))}}{{\partial F(\mathit{\boldsymbol{v}})}} $ |
将原始样本一一代入式中,即得到转换后的样本数据。以此类推,由下述公式
| $ F({x_i}\mathit{\boldsymbol{v}}) = \frac{{\partial {C_{{x_i}{x_j}|{\mathit{\boldsymbol{v}}_{ - j}}}}(F({x_i}|{\mathit{\boldsymbol{v}}_{ - j}}),F({x_j}|{\mathit{\boldsymbol{v}}_{ - j}}))}}{{\partial F({x_j}|{\mathit{\boldsymbol{v}}_{ - j}})}},$ | (14) |
在得到F(xi| v- j)和F(x j| v- j)的样本数据后,拟合出Cxix j| v - j,再由式(14)即可得到下一步拟合所需的样本数据,重复这样的步骤直到PCC中的所有copula密度都得到拟合,就得到了X=(X1, …, Xn)的联合概率密度。
为了后文叙述方便,这里定义h(x, v)= Cx v (x, v) v,则F(x| v)=h(F(x), F(v))。由于PCC的多样性,如何构造和选取PCC,是应用这一方法的关键。藤结构的提出完美解决了PCC的构造问题,为这一方法奠定了理论基础。
2.2 藤结构Bedford和Cooke[31]提出了用图来表示PCC,即将每一个PCC分解用藤结构来刻画,藤结构有如下定义:
定义2.1 记T1, …, Tn-1为一列树,其中树Ti的点集和边集分别为Ni和Ei,且满足
1) N1={1, …, n}.
2) 对于i=2, …, n-1,Ni=Ei-1.
则称V=(T1, …, Tn-1)为一个n元藤结构。若V还满足:
3)(正则条件)对所有i=2, …, n-1,只要a, b∈Ni且{a, b}∈Ei,那么a, b作为树Ti-1中的两条边,在树Ti-1中必有一个共同的顶点。
则称V为一个n元R藤,或称为正则藤。
利用R藤与PCC之间建立联系,本质上是将式(13)的分解形式用图来表示,式中的边缘分布或条件分布与R藤中某一棵树的顶点对应,而连接这两个分布的copula函数,则对应树中连结两个顶点的边。具体地,记E0=N1,对i=1, 2, …, n-1和任意ei={a, b}∈Ei,a, b∈Ei-1,令
| $ {D_{{e_i}}} = {\rm{ }}{U_a} \cap {U_b}, {C_{{e_i}, a}} = {\rm{ }}{U_a}\backslash {D_{{e_i}}}, {C_{{e_i}, b}} = {\rm{ }}{U_b}\backslash {D_{{e_i}}}. $ |
将每条边e={a, b}对应于连接了给定XDe时XCe, a和Ce, b的条件分布的二元copula函数,可以证明,|Ce, a|=|Ce, b|=1,且下式给出了联合密度的一个PCC
| $ f({x_1}, \ldots {x_n}) = {\rm{ }}{f_1} \ldots {f_n}\prod\limits_{i{\rm{ }} = 1}^{n - 1} {\prod\limits_{e \in {E_i}} {{c_{{C_{e, a}}, {C_{e, b}}^{|{\rm{ }}{D_e}}}}} } ({F_{{C_{e, {a^{|{\rm{ }}{D_e}}}}}}}, {F_{{C_{e, {b^{|{\rm{ }}{D_e}}}}}}}).{\rm{ }} $ | (15) |
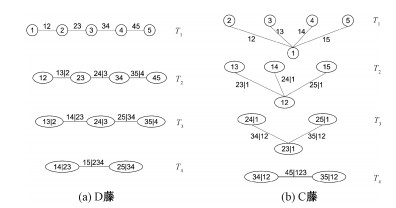
事实上,对任意一种PCC,若根据其n(n-1)/2个copula密度,对应构造出其图结构,则会得到一个R藤,反过来,对于任意一个R藤,可以由式(15)写出这个R藤唯一决定的PCC。图 1例举了D藤和C藤结构,其中“|”的左边为变量集,右边为条件集,对每条边连结的顶点集合求交集,即可得到这条边所对应的条件集De,再由对称差得出变量集Ce, a∪Ce, b。D藤和C藤可理解为R藤的两个极端情形,其定义分别为:
|
Download:
|
| 图 1 D藤和C藤 Fig. 1 D-vine and C-vine | |
·若T1中顶点的最大度数是2,则称其为D藤。
·若对i=1, …n-1,每个Ti都有一个度数为n-i的顶点,则称其为C藤。
理论上可以对所有可能的PCC做拟合,再比较它们的优劣,但随着维数的增高,这样的做法是不切实际的。利用Kendall’s τ秩相关系数及分布之间的条件独立,可以对R藤的选取提供依据。若模型中的变量存在条件独立性,则它们的条件分布对应的copula函数为乘积copula:C(u, v)=uv,其对应的copula密度为c(u, v)=1,这样就使得模型得到了简化。通常认为,有着较强相依性的变量之间的拟合应更加追求准确性,本文选取的相依性度量为Kendall’s τ秩相关系数,基于下述理由认为,其绝对值大的变量组合更应优先被准确地拟合:
· R藤中第1棵树的拟合效果,往往对整个模型影响较大。
· 很多不同类型的copula函数都可以较好地拟合存在独立性的数据,并且独立性相对应的参数取值相同或相近。
· 在实际应用中,往往可以认为数据的相依关系是由部分变量产生的,而非全部变量,若在T1中选择相依性强的变量组合进行拟合,则后续的转换变量之间的相依性在相比较之下更弱甚至可以认为是独立的。
所以,本文结合最大生成树算法来构造PCC。对树N1生成的完全图,定义其每条边的边值为Kendall’s τ秩相关系数的绝对值,由如下最大生成树算法生成T1;
·从N1中任选一点,并从连结它的所有边中选择边值最大的作为第1条边。
·从连结了已被选取的边中任一顶点的所有边中选择边值最大的一条边,添加到已选取的边中。
· 重复上一步骤直到所有顶点都被已选取的边连结到为止,由此得到的树即为最大生成树T1。
2.3 藤copula方法与SMAA的结合利用PCC方法需要获取模型中多元随机变量的一组独立同分布样本,在其边缘分布已知甚至未知的情形下,利用样本和适当的二元copula构造出这个多元随机变量的联合分布。但实际情况中,我们获取的数据可能是时间序列,不能作为独立同分布的样本。这样的情况,可以先采用AMRA和GARCH模型[32]对其边缘分布进行拟合,去除自相关和异方差性,得到残差样本序列再由其经验分布转化为均匀分布的值,即可作为独立样本处理。
对于本文所提出的SMAA与藤copula相结合的方法,其具体应用步骤可归纳如下:
1) 获取随机变量(ξij)m×n的一组独立同分布的样本,必要时可采用AMRA和GARCH模型将其转化为标准均匀分布。为方便起见,(ξij)m×n可重新标号并记为(X1, …, XN)。
2) 对所有变量组合计算Kendall’s τ秩相关系数。
3) 根据2.2节中的最大生成树算法,得到最大生成树。
4) 结合多种方法,选择不同类型copula函数拟合最大生成树中每条边对应的变量组合,并用几种检验方法比较其优劣,最终确定copula函数类型及其参数。在拟合之前,可以先对数据做独立性检验,若认为独立性成立,则采用独立copula函数简化模型。
5) 由上一步得出的copula函数及其参数计算得到转换后的样本。
6) 根据转换后的样本,对所有可能的样本组合计算其经验分布的Kendall’s τ秩相关系数。这里,可能的样本组合是指必须满足R藤的正则条件。
7) 重复步骤3)到步骤5),直到得到完整的mn元R藤,以及所有需要拟合的copula函数及参数。
8) 因为SMAA所计算的积分是对上一步中得到的非常复杂的分布所做的积分,因而需要采用蒙特卡罗模拟的方法来计算积分的近似值。依据拟合出的(ξij)m×n的联合分布,模拟出大样本,根据模拟样本来计算SMAA问题中的可接受度,中心权重向量以及置信度等指标。
9) 对上一步的计算结果进行分析,比较不同选择的优劣。
注意到,最大生成树算法是对连通图进行的,因为在构造T1时,是从完全图开始的,算法条件当然满足。而在后续构造中,不难验证,定义2.1的正则条件确保了步骤5)中所有可能的样本组合构成一个连通图,即对每个已知的Ti-1,Ti的所有可能的备选边构成了集合
| $ {F_{{C_{e,a}}|{D_e}}}({X_{{C_{e,a}}}}|{\mathit{\boldsymbol{v}}_{{D_e}}}),{F_{{C_{e,b}}|{D_e}}}({X_{{C_{e,b}}}}|{\mathit{\boldsymbol{v}}_{{D_e}}}). $ |
其中vDe表示指标集De所对应的随机变量集合。注意到定义2.1的正则条件保证了a, b有一个Ti-1中的公共元素,不妨记为a={a1, a2}, b={a2, b2},则结合Ua的定义,不难验证Ce, a=Ca, a1, De=Da∪Ca, a2,进而由式(14)可计算转换变量如下
| $ \begin{array}{l} {F_{{C_{e, a}}|{\rm{ }}{D_e}}}({X_{{C_{e, a}}}}|{\mathit{\boldsymbol{v}}_{{D_e}}}) = \\ \frac{{\partial {C_{{C_a}|{\mathit{\boldsymbol{v}}_{{D_a}}}}}({F_{Ca, {a_1}^{|{\rm{ }}{D_a}}}}({x_{{C_{a, {a_1}}}}}|\mathit{\boldsymbol{v}}{D_a}), F{C_{a, {a_2}}}|{\rm{ }}{D_a}(x{C_{a, {a_2}}}|{\mathit{\boldsymbol{v}}_{{D_a}}}))}}{{\partial {F_{{C_{a, {a_2}}}}}_{|{\rm{ }}Da}({x_{{C_{a, {a_2}}}}}|{\mathit{\boldsymbol{v}}_{{D_a}}})}} = \\ h({F_{Ca, {a_2}^{|{\rm{ }}{D_a}}}}({x_{{C_{a, {a_1}}}}}|{\mathit{\boldsymbol{v}}_{{D_a}}}), {F_{Ca, {a_2}^{|{\rm{ }}{D_a}}}}({x_{{C_{a, {a_2}}}}}|{\mathit{\boldsymbol{v}}_{{D_a}}})) \end{array}. $ |
式中Ca=Ca, a1∪Ca, a2,且转换变量FCa, a1|Da(xCa, a1| vDa), FCa, a2|Da(XCa, a2| vDa)已经在上一步的递推过程中得到。将XCa, a1, XCa, a2的样本值一一代入即得到了转换样本。
尽管上述步骤看似复杂,但计算机程序可以很快捷地得到藤copula拟合的分布,而接下来的SMAA-2分析与以往方法的区别则主要是蒙特卡罗模拟的不同。Lahdelma等[23]建议使用高斯分布来拟合问题中不确定的标准值,而高斯分布本身具有形式简单、计算容易的特点。在进行SMAA分析时所需要计算的积分,一般不需要采用数值方法或是蒙特卡罗模拟的方法,而对于本文建议的藤copula拟合出的分布而言,要进行后续的SMAA-2分析,则必须要用到蒙特卡罗模拟进行近似。虽然复杂性略有提高,但通过计算机程序可以大大简化工作量。总体上,略微提高的复杂度换来的是更加准确的拟合结果,进而使SMAA分析得到的决策建议更加可靠,这是本文方法的创新以及优势所在。
3 模拟分析 3.1 模拟算例分析本文假定的研究案例有A、B、C 3个选择方案,而每种选择的总效用都由2个判别标准来量化,且这些标准的值是随机的,这些随机标准的值一共构成了6个决策变量,也组成了一个6维的随机向量。假定这些决策变量都服从标准均匀分布,之所以可以这样假定,是因为随机变量的分布函数自身是服从均匀分布的,因此对于实际数据,都可以进行一步转化,得到其分布函数的函数值,再进行数据分析。而对于效用函数,为了简化问题,本文假定每个决策变量的效用函数都为标准均匀分布的分布函数,这样便省去了对每个决策变量效用的计算。当然,在实际应用中,会根据每个决策变量的实际意义来分别定义其效用函数,并对所有决策变量都计算出效用函数值再进行下一步分析。对于模拟案例中的数据,本文用一个给定的R藤结构表示它们的联合分布。这个R藤的结构矩阵为
| $ \left[ {\begin{array}{*{20}{c}} 6&0&0&0&0&0\\ 2&5&0&0&0&0\\ 3&2&2&0&0&0\\ 1&3&3&3&0&0\\ 4&1&4&4&4&0\\ 5&4&1&1&1&1 \end{array}} \right]. $ |
结构矩阵与藤结构是多对一的关系[33],它将藤结构转化为矩阵来表示,进而可方便地应用于计算机程序中,实现复杂的计算。结构矩阵为下三角矩阵,且右边的任意列中的元素都包含于它左边的列中,每个藤结构可以用多种等价的矩阵形式来表示,而每个结构矩阵反过来可得到唯一与之对应的藤结构。以本例的矩阵第1列为例,对角线上的变量与最后一行的变量连结了一条边,这些边构成了藤结构中的第一棵树。然后对角线上的变量与倒数第2行的变量在以最后一行的变量为条件下的条件变量连结了一条边,而这些边则构成了藤结构中的第2棵树,依次类推,这个矩阵对应的5棵树如图 2所示。

|
Download:
|
| 图 2 假定的R藤结构 Fig. 2 The assumed R-vine | |
按照同样的方式,可以用矩阵来记录藤结构每条边所对应的copula函数的函数族以及函数参数,它的copula函数族矩阵如下
| $ \left[ {\begin{array}{*{20}{c}} 0&0&0&0&0&0\\ 3&0&0&0&0&0\\ 3&2&0&0&0&0\\ 3&3&3&0&0&0\\ 3&4&4&4&0&0\\ 3&4&1&1&3&0 \end{array}} \right]. $ |
其中
· 1=Gaussian copula.
· 2=Student t copula.
· 3=Clayton copula.
· 4=Gumbel copula.
因为本例中都是单参数copula,因此只需要1个矩阵来记录其各个参数,如下述矩阵所示
| $ \left[ {\begin{array}{*{20}{c}} 0&0&0&0&0&0\\ {0.5}&0&0&0&0&0\\ {0.4}&{0.2}&0&0&0&0\\ {1.4}&{0.9}&{1.1}&0&0&0\\ {1.6}&{1.5}&{1.6}&{1.9}&0&0\\ {3.1}&{3.9}&{0.9}&{0.5}&{4.8}&0 \end{array}} \right]. $ |
通过这3个矩阵的信息,即给定了决策变量的联合分布。由这个联合分布,本文模拟出10 000个决策样本。对这些样本进行直接的SMAA分析。分析得到的结果如表 1所示。
|
|
表 1 决策样本的秩可接受度 Table 1 Rank acceptability of sample data |
由表 1可知,C选择的最优可接受度最大,为0.407;A选择的最优可接受度次之,为0.303 8;B选择最低,为0.289 2。可以得到结论: C为最优选择,A选择次之,B选择最差。如果将秩为2的可接受度也考虑进来的话,不难发现B选择的秩可接受度最大。并且前两个秩的可接受度之和也是最大,说明B选择不太可能成为最差的选择,在实际应用中可以把这种情况视为一种折中策略。
用这些样本,以及第2节介绍的方法,可以拟合出由[3个选择×2个准则]组成的6维随机变量的联合分布,具体的计算步骤可以由R软件实现,计算得出的联合分布依然由多个矩阵来表示,包括藤结构矩阵,copula函数族矩阵和对应的1个或2个copula参数矩阵,其中R藤结构矩阵为
| $ \left[ {\begin{array}{*{20}{c}} 6&0&0&0&0&0\\ 4&3&0&0&0&0\\ 5&4&0&0&0&0\\ 3&5&4&0&0&0\\ 2&1&5&4&4&0\\ 1&2&2&5&5&5 \end{array}} \right] $ |
结构矩阵对应的5棵树如图 3所示

|
Download:
|
| 图 3 拟合的R藤结构 Fig. 3 The fitted R-vine | |
它的copula函数族矩阵如下
| $ \left[ {\begin{array}{*{20}{c}} 0&0&0&0&0&0\\ 3&0&0&0&0&0\\ 3&3&0&0&0&0\\ 3&2&2&0&0&0\\ 2&2&2&2&0&0\\ 3&1&1&2&4&0 \end{array}} \right] $ |
它们对应的参数矩阵如下
| $ {\begin{array}{*{20}{c}} {0.000{\rm{ }}00}&{0.000{\rm{ }}000}&{0.000{\rm{ }}00}&{0.000{\rm{ }}00}&{0.000{\rm{ }}00}&{0.000{\rm{ }}00}\\ {0.{\rm{ }}374{\rm{ }}20}&{0.000{\rm{ }}00}&{0.000{\rm{ }}00}&{0.000{\rm{ }}00}&{0.000{\rm{ }}00}&{0.000{\rm{ }}00}\\ {0.{\rm{ }}233{\rm{ }}49}&{0.{\rm{ }}357{\rm{ }}03}&{0.000{\rm{ }}00}&{0.000{\rm{ }}00}&{0.000{\rm{ }}00}&{0.000{\rm{ }}00}\\ {0.{\rm{ }}173{\rm{ }}14}&{0.{\rm{ }}370{\rm{ }}41}&{0.{\rm{ }}221{\rm{ }}99}&{0.000{\rm{ }}00}&{0.000{\rm{ }}00}&{0.000{\rm{ }}00}\\ {0.{\rm{ }}372{\rm{ }}42}&{ - 0.{\rm{ }}490{\rm{ }}58}&{0.{\rm{ }}282{\rm{ }}41}&{0.{\rm{ }}314{\rm{ }}27}&{0.000{\rm{ }}00}&{0.000{\rm{ }}00}\\ {3.{\rm{ }}770{\rm{ }}64}&{0.{\rm{ }}722{\rm{ }}74}&{0.{\rm{ }}901{\rm{ }}72}&{0.{\rm{ }}900{\rm{ }}65}&{3.{\rm{ }}962{\rm{ }}06}&{0.000{\rm{ }}00} \end{array}} $ |
由于拟合过程中考虑了t分布等双参数型的copula函数,因此还需要第2参数矩阵来记录其对应的自由度。它们的自由度如下所示
| $ \left[ {\begin{array}{*{20}{c}} {0.000{\rm{ }}00}&{0.000{\rm{ }}000}&{0.000{\rm{ }}00}&{0.000{\rm{ }}00}&{0.000{\rm{ }}00}&{0.000{\rm{ }}00}\\ {0.000{\rm{ }}00}&{0.000{\rm{ }}00}&{0.000{\rm{ }}00}&{0.000{\rm{ }}00}&{0.000{\rm{ }}00}&{0.000{\rm{ }}00}\\ {0.000{\rm{ }}00}&{0.{\rm{ }}000{\rm{ }}00}&{0.000{\rm{ }}00}&{0.000{\rm{ }}00}&{0.000{\rm{ }}00}&{0.000{\rm{ }}00}\\ {0.000{\rm{ }}00}&{18.{\rm{ }}743{\rm{ }}01}&{4.{\rm{ }}624{\rm{ }}36}&{0.000{\rm{ }}00}&{0.000{\rm{ }}00}&{0.000{\rm{ }}00}\\ {21.{\rm{ }}754{\rm{ }}09}&{8.{\rm{ }}835{\rm{ }}24}&{5.{\rm{ }}855{\rm{ }}37}&{4.{\rm{ }}492{\rm{ }}27}&{0.000{\rm{ }}00}&{0.000{\rm{ }}00}\\ {0.000{\rm{ }}00}&{0.000{\rm{ }}00}&{0.000{\rm{ }}00}&{0.000{\rm{ }}00}&{0.000{\rm{ }}00}&{0.000{\rm{ }}00} \end{array}} \right] $ |
可以看到,拟合出的R藤与原假设的藤结构并不相同,但是,通过拟合出的联合分布,再次进行SMAA分析,分析得到结果如表 2所示。
|
|
表 2 拟合模型的秩可接受度 Table 2 Rank acceptability of the fitted model |
由表 2可知,C选择的最优可接受度最大,为0.405 9;A选择的最优可接受度次之,为0.340 1;B选择最低,为0.254 0。可以得到结论,C为最优选择,A选择次之,B选择最差。这与原假设的模型分析结果完全相符。
结论:如果不考虑6个变量相依结构,即它们相互独立,那么对于本例而言,各个决策变量的效用彼此没有不同,用SMAA分析会得到3个选择的秩可接受度近乎相等,这显然与假设案例的结果是不相符的。而考虑相依结构得到的结果与假设案例的实际情况是一致的。这说明,考虑变量间的相依关系,用藤copula拟合出联合分布,再进行SMAA分析的方法是准确的、贴合实际的,能够给决策者提供科学准确的参考依据。
3.2 对比分析在SMAA方法的研究领域,已经有文献考虑了决策变量之间的相依关系,并采用常用的多元分布来取代独立分布。Lahdelma等[23]提出用独立分布来处理高维数据是不准确不合理的,并将高斯分布(多元正态模型)运用到SMAA方法中,假定随机的决策变量服从多元正态分布,再由秩可接受度来评估各个选择的优劣,其分析结果与独立假设下计算的结果有明显的区别。在金融研究领域,copula方法被广泛应用,但应用较多的往往是形式上较为简单的函数族,例如椭圆型copula函数族[34]。在椭圆型copula函数族中,高斯copula是最简单实用的一种,在实证应用研究中经常发挥重要作用。因此,本文将多元正态模型和高斯copula这两种函数模型加入到模拟实验中,与R藤模型进行对比,分析出不同模型的优劣。
这里分别用多元正态模型以及高斯copula模型对3.1节中的10 000 000个原始样本进行拟合,通过拟合出结果分别进行SMAA分析,然后与用样本直接计算SMAA以及用藤copula拟合计算SMAA的结果进行对比。结果如表 3所示。
|
|
表 3 不同拟合模型的对比分析 Table 3 Comparison between those fitted models |
从表 3中可以看出,3种拟合方法得到的结果都是C选择最优,这与直接通过样本计算得到的结果是一致的。在准确性方面,观察一下C选择的可接受度的数值,很显然,这3种方法的值几乎一致。但相对于参考样本的直接计算值,藤copula的误差为0.27 %;多元正态的误差为0.93 %;高斯copula的误差为0.52 %。因此得到以下结论:在样本数据比较常规(生成样本时选用的copula函数族以及参数都比较常规)时,3种方法的计算结果都比较准确,藤copula方法相对误差最小,即本文提出的方法有一定的优势。
3.3 对尾部相依结构样本进行对比分析在金融和管理领域,一些极端的数据通常容易引起广泛关注,就像数据之间的非线性关系一样,只看线性关系是没有意义的。同样地,秩相关也不能完美地描述所有的相依关系。实证研究中,需要使用尾部相依关系(二元变量中数据取值特别大或特别小时的相依关系)。为了检验本文提出的方法对实际问题的实用性,本文建立一种具有尾部相依结构的分布,并模拟生成出一组具有尾部相依性的数据,然后用藤copula、多元正态、高斯copula模型分别拟合后的结果与SMAA方法直接分析的结果进行对于分析,与进行SMAA分析的结果进行对比,得出结论和建议。

|
Download:
|
| 图 4 常用copula函数的等高线图 Fig. 4 Contour map of common copulas | |
由图 4可知,Clayton copula和Gumbel copula(在copula函数族矩阵中用3和4表示)具有尾部相依性,随着τ系数的增大而愈加明显。
从该性质出发,同样假定的研究案例是3个选择、2个标准的6维随机变量,使用图 2的R藤结构表示它们的联合分布。对于它的copula函数族矩阵,全部选用Clayton copula和Gumbel copula,矩阵如下
| $ \left[ {\begin{array}{*{20}{c}} 0&0&0&0&0&0\\ 3&0&0&0&0&0\\ 3&4&0&0&0&0\\ 3&3&3&0&0&0\\ 3&4&4&4&0&0\\ 3&4&4&4&3&0 \end{array}} \right] $ . |
其中3代表Clayton copula,4代表Gumbel copula。它们是单参数copula函数,为了得到更明显的尾部相依性,利用大于5的参数使得τ系数大于0.7。得到对应的参数矩阵
| $ \left[ {\begin{array}{*{20}{c}} 0&0&0&0&0&0\\ 5&0&0&0&0&0\\ 7&4&0&0&0&0\\ {19}&{17.9}&{6.1}&0&0&0\\ {26}&{6.5}&{5.6}&7&0&0\\ {8.1}&{19}&{10.9}&{26}&8&0 \end{array}} \right] $ |
通过这些参数,模拟出10 000个新样本。然后分别用藤copula模型、多元正态模型以及高斯copula模型对于模拟得到的10 000个新样本进行拟合,通过拟合出的联合分布,对于各个随机模型进行SMAA分析。最后对比计算结果与用新样本直接进行SMAA分析的结果(对比结果见表 4)。
|
|
表 4 尾部相依情形下的对比分析 Table 4 Comparison analysis when tail-dependency exists |
从分析结果中可以看出,用藤copula拟合得到的结果是B选择最优,多元正态和高斯copula拟合得到的结果是C选择最优。对于新样本直接计算的实际结果而言,B为最佳选择,这与本文提出的方法(藤copula拟合)结果一致。结果表明在数据出现尾部相依性时,藤copula方法得到的结果与实际情况一致,而多元正态和高斯copula方法差距较大,无法提供精准的参考信息。因而选择方法时,建议使用藤copula方法拟合出联合分布,再进行SMAA分析,该方法可以适用于不同分布类型的数据,为决策者提供更准确和实用的参考。
4 结语本文对于藤copula的原理及其相关性质进行详细介绍,该函数的适用范围较广,可应用于各种数据,具有一定的优势。通过实例研究,结合藤copula拟合样本数据得到样本联合分布的方法,以及应用SMAA方法计算各个备选方案的优劣的具体步骤。此外,与多元正态模型和高斯copula模型等传统方法的对比分析进一步证明了藤copula模型与SMAA方法结合的优势:准确度高、实用性强。
在实际案例中处理决策问题时,决策变量随机不确定性会导致观察值的减少。如果这些样本直接进行SMAA分析,由此产生的决策可能只适用于当前的具体情况,无法将该决策推广到更加全面的范围。因此,引入联合分布函数和藤系copula模型来拟合这些决策变量的联合分布函数,并采用SMAA方法进行决策分析。最后,在联合分布函数计算的基础上,评估不同备选方案的优缺点。期望值将更科学、更严谨、更能代表整体。
然而,不同的拟合方法将得到不同的联合分布,这会对SMAA分析的结果有所影响。Lahdelma等[23]将多元正态模型引入到SMAA方法中。而多元正态模型只能拟合考虑变量之间的线性相关条件下边际分布为正态分布的决策变量。模拟实验的研究结果表明,由于数据存在尾部相依性,对于某些模型(比如多元正态模型,高斯copula模型)并不适用,得到的结论甚至会有错误。但藤copula模型的分析计算结果并不会出现这类问题。
由于数据来源有限,尚未获得可用于数据分析的大样本实际案例数据,因此未对实际问题并没有进行数据与决策的分析,本文主要是在理论上提出了这种创新方法,通过实例模拟来验证该方法的主要步骤和优点。在模拟过程中,所有考虑的决策变量均为标准化均匀分布,效用函数定义为变量的分布函数。对于实际数据,必须充分考虑到符合实际情况的效用函数以及每个决策变量各自的边际分布。本文提出的方法进一步提高了SMAA方法的应用价值。在多标准决策领域,还有其他流行的研究方法,如DEMATEL模型和网络分析。DEMATEL更注重各种决策因素之间的逻辑关系和相互影响。并充分利用该领域专家的相关经验和知识建立决策模型,同时又具有这种网络分析方法的特点。
本文研究发现,与其他借助于逻辑和经验的方法相比,SMAA方法对于权重信息缺失,或者说缺少足够的专家经验时的应用适应性更强,这种方法对数据更加重视,从大数据中挖掘决策意见,而copula方法加强了对于数据的重视程度,充分发挥数据利用的优势,但对实际问题的样本数据量也有一定的要求。因此,决策者可能会根据实际情况采取不同的方法。
对于未来的研究方向,除解决现实生活中的一些决策问题的实际应用研究外,本文的方法还可以扩展到研究如何将copula方法与精细化的随机多准则接受度分析方法相结合,例如,可以和SMAA-O,SMAA-TRI,SMAA-D等方法结合使用。对于一些比较复杂的实际问题,本文方法可以与DEMATEL模型和网络分析法等方法结合使用,或者进行对比分析,考查不同方法的优缺点,研究出更多有意义的成果。
| [1] |
Keeney R L, Raiffa H, Meyer R F. Decisions with multiple objectives: preferences and value trade-offs[M]. Cambridge, UK: Cambridge university press, 1993.
|
| [2] |
Roy B. Decision aiding: major actors and the role of models[M]//Multicriteria methodoly for decision making. Boston, USA: Springer, 1996: 237-267.
|
| [3] |
Brans J P, Mareschal B. Promethee methods[M]//Multiple criteria decision analysis. New York, USA: Springer, 2005: 163-186.
|
| [4] |
Xu X Z. The SIR methods: a superiority and inferiority ranking method for multiple criteria decision making[J]. European Journal of Operational Research, 2001, 131(3): 587-602. Doi:10.1016/S0377-2217(00)00101-6 |
| [5] |
Lahdelma R, Hokkanen J, Salminen P. SMAA-stochastic multiobjective acceptability analysis[J]. European Journal of Operational Research, 1998, 106(1): 137-143. Doi:10.1016/S0377-2217(97)00163-X |
| [6] |
Lahdelma R, Salminen P. SMAA-2:stochastic multicriteria acceptability analysis for group decision making[J]. Operations Research, 2001, 49(3): 444-454. Doi:10.1287/opre.49.3.444.11220 |
| [7] |
Lahdelma R, Miettinen K, Salminen P. Ordinal criteria in stochastic multicriteria acceptability analysis (SMAA)[J]. European Journal of Operational Research, 2003, 147(1): 117-127. Doi:10.1016/S0377-2217(02)00267-9 |
| [8] |
Yu W. ELECTRE TRI: aspects m thodologiques et manuel d utilisation[D]. Paris, France: Universit de Paris-Dauphine, 1992.
|
| [9] |
Tervonen T, Lahdelma R, Dias J A, et al. SMAA-TRI: a parameter stability analysis method for ELECTRE-TRI[C]//Kiker G A, Linkov I. Environmental Security in Harbors and Coastal Areas. Berlin, Germany: Springer, 2007: 217-231.
|
| [10] |
Tervonen T, Figueira J R, Lahdelma R, et al. Towards robust ELECTRE Ⅲ with simulation: theory and software of SMAA-Ⅲ[J]. European Journal of Operational Research, under review, 2007. |
| [11] |
Lahdelma R, Salminen P. Stochastic multicriteria acceptability analysis using the data envelopment model[J]. European Journal of Operational Research, 2006, 170(1): 241-252. Doi:10.1016/j.ejor.2004.07.040 |
| [12] |
Lahdelma R, Salminen P. Prospect theory and stochastic multicriteria acceptability analysis (SMAA)[J]. Omega, 2009, 37(5): 961-971. Doi:10.1016/j.omega.2008.09.001 |
| [13] |
Corrente S, Figueira J R, Greco S. The SMAA-PROMETHEE method[J]. European Journal of Operational Research, 2014, 239(2): 514-522. Doi:10.1016/j.ejor.2014.05.026 |
| [14] |
Tervonen T, Lahdelma R. Implementing stochastic multicriteria acceptability analysis[J]. European Journal of Operational Research, 2007, 178(2): 500-513. Doi:10.1016/j.ejor.2005.12.037 |
| [15] |
Hokkanen J, Lahdelma R, Miettinen K, et al. Determining the implementation order of a general plan by using a multicriteria method[J]. Journal of Multi-Criteria Decision Analysis, 1998, 7(5): 273-284. Doi:10.1002/(SICI)1099-1360(199809)7:5<273:AID-MCDA198>3.0.CO;2-1 |
| [16] |
Hokkanen J, Lahdelma R, Salminen P. A multiple criteria decision model for analyzing and choosing among different development patterns for the Helsinki cargo harbor[J]. Socio Economic Planning Sciences, 1999, 33(1): 1-23. Doi:10.1016/S0038-0121(98)00007-X |
| [17] |
Hokkanen J, Lahdelma R, Salminen P. Multicriteria decision support in a technology competition for cleaning polluted soil in Helsinki[J]. Journal of Environmental Management, 2000, 60(4): 339-348. Doi:10.1006/jema.2000.0389 |
| [18] |
Lahdelma R, Salminen P, Hokkanen J. Locating a waste treatment facility by using stochastic multicriteria acceptability analysis with ordinal criteria[J]. European Journal of Operational Research, 2002, 142(2): 345-356. Doi:10.1016/S0377-2217(01)00303-4 |
| [19] |
Tervonen T, Hakonen H, Lahdelma R. Elevator planning with stochastic multicriteria acceptability analysis[J]. Omega, 2008, 36(3): 352-362. Doi:10.1016/j.omega.2006.04.017 |
| [20] |
Kangas J, Hokkanen J, Kangas A S, et al. Applying stochastic multicriteria acceptability analysis to forest ecosystem management with both cardinal and ordinal criteria[J]. Forest Science, 2003, 49(6): 928-937. |
| [21] |
Xia Q, Hua Z S, Song S L. Location selection of distribution centers based on SMAA[J]. Lecture Notes in Electrical Engineering, 2014, 273(1): 213-220. Doi:10.1007/978-3-642-40640-9-28 |
| [22] |
Zhu F L, Zhong P G, Wu Y N, et al. SMAA-based stochastic multi-criteria decision making for reservoir flood control operation[J]. Stochastic Environmental Research and Risk Assessment, 2017, 31(6): 1485-1497. Doi:10.1007/s00477-016-1253-3 |
| [23] |
Lahdelma R, Makkonen S, Salminen P. Multivariate gaussian criteria in SMAA[J]. European Journal of Operational Research, 2006, 170(3): 957-970. Doi:10.1016/j.ejor.2004.08.022 |
| [24] |
Genest C, Favre A C. Everything you always wanted to know about copula modeling but were afraid to ask[J]. Journal of Hydrologic Engineering, 2007, 12(4): 347-368. Doi:10.1061/(asce)1084-0699(2007)12:4(347) |
| [25] |
Genest C, Rémillard B, Beaudoin D. Goodness-of-fit tests for copulas: a review and a power study[J]. Insurance Mathematics and Economics, 2009, 44(2): 199-213. Doi:10.1016/j.insmatheco.2007.10.005 |
| [26] |
Joe H. Families of m-variate distributions with given margins and m (m-1)/2 bivariate dependence parameters[J]. Lecture Notes-Monograph Series, 1996, 28: 120-141. |
| [27] |
Bedford T, Cooke R M. Probability density decomposition for conditionally dependent random variables modeled by vines[J]. Annals of Mathematics and Artificial Intelligence, 2001, 32(1): 245-268. Doi:10.1023/A:1016725902970 |
| [28] |
Aas K, Czado C, Frigessi A, et al. Pair-copula constructions of multiple dependence[J]. Insurance Mathematics and Economics, 2009, 44(2): 182-198. Doi:10.1016/j.insmatheco.2007.02.001 |
| [29] |
Sklar A. Fonctions de répartition à n dimensions et leurs marges[J]. Publications de l'Institut de Statistique de l'Uni-versité de Paris, 1959(8): 229-231. |
| [30] |
Genest C, Rivest L P. Statistical inference procedures for bivariate archimedean copulas[J]. Journal of the American Statistical Association, 1993, 88(423): 1034-1043. Doi:10.1080/01621459.1993.10476372 |
| [31] |
Bedford T, Cooke R M. Vines-a new graphical model for dependent random variables[J]. The Annals of Statistics, 2002, 30(4): 1031-1068. Doi:10.1214/AOS[WTB4]%2F1031689016 |
| [32] |
叶五一, 郭人榛, 缪柏其. 基于R藤copula变点模型的金砖四国金融传染性与稳定性检验[J]. 中国科学技术大学学报, 2018, 48(8): 655-666. Doi:10.3969/j.issn.0253-2778.2018.08.009 |
| [33] |
Diβmann J F. Statistical inference for regular vines and application[D]. Munich, Germany: Technische Universität München, 2010.
|
| [34] |
Joe H, Kurowicka D. Dependence modeling: vine copula handbook[M]. Singapore: World Scientific, 2010. Doi:10.1142/7699
|
 2022, Vol. 39
2022, Vol. 39 


