2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
甚高频数据交换系统(VHF data exchange system, VDES)包括地面与卫星两大子系统, 是e航海战略的核心通信技术之一, 也是未来海事通讯技术的发展趋势[1]。目前, VDES系统的技术标准的制定尚处于初级阶段:Luglio等[2]从信道组成和接入方案等方面对VDES系统地面和卫星系统通信标准进行了技术分析;国际航标协会(International Association of Lighthouse Authorities, IALA)在2019年发布的G1139协议[3]对VDE-SAT业务下行链路设计指标制定了相关标准, 但协议仍需进一步的研究论证。通过构建信道模型可以近似描述真实的通信信道, 为后续VDES系统设计方案的策划和制定提供重要的理论支持。
针对星船通信下行链路信道建模问题,夏明华等[4]指出,卫星到地面终端的信道模型也基本适用于卫星到船舶的信道建模,例如Corazza信道模型[5],longley-Rice模型[6]等;刘媛美[7]则在传统的C.Loo信道模型上进行了适应性改进。然而上述模型均未考虑海上通信传播环境的复杂性。实际上, 海面是一个时变、不规则的随机粗糙反射面, 传输电磁波时存在镜面反射和漫反射, 由此带来的多径衰落会严重影响通信质量。还有一些学者将VDES信道简单建模为加性高斯白噪声AWGN信道[8]或者莱斯信道[9]。然而海上卫星通信具有更大的多普勒频移和传输时延, 其多径传播几何模型受地球曲率的影响更大。因此, 简单的AWGN信道和莱斯信道模型无法准确描述星船通信信道。
此外,Giambene等[10]通过对挪威航天局发射的NorSat-2号卫星得到的实验数据进行拟合,得出Gamma分布拥有着最佳拟合的结论;Bråten等[11]利用KV Harstad执法船上获得的数据集分析了NorSat-2号卫星在下行链路的测量结果,得出信道衰落接近标准差为4.2 dB对数正态分布。然而,上述建模方法都是通过对实验数据进行拟合得到信道特征模型,对于实验数据具有极大的依赖性,仅仅适用于特定通信链路的场景,并没有对不同海况下的模型参数进行分析、修正,因此该信道建模方法不具有通用性。
基于上述分析, 本文提出一种新的针对海上卫星通信的VDE-SAT下行链路信道建模方法。该方法通过建立基于球坐标系的星船几何传播模型, 充分考虑地球曲率对于信号传播路径的影响,通过参数化海面散射特性,考虑不同海况对信号传播路径的影响。最后通过仿真得到不同海况下VDE-SAT下行链路的信号误码率曲线, 分析不同海况对信号接收特性的影响, 得出的结论与现有文献结论相吻合,验证了模型的准确性。
1 海面电磁散射特性 1.1 海浪参数分析海浪的时变性和不规则性导致海上信道复杂多变, 多径衰落显著。为有效描述海面的电磁散射特性, 需要根据海面的统计特性对其进行参数化分析。
1) 均方根波高
目前多用世界气象组织(World Meteorological Organization, WMO)和Douglas根据不同波浪高度为划分依据的海情级来描述海浪状态[7], 如表 1所示。
|
|
表 1 不同海情级的划分 Table 1 Division of different sea level |
海情级的划分是在数学上对海上风力大小的表征[7]。其中的均方根波高定义为海面波浪高度的均方根值, 该值会对海上多径信道模型的参数产生影响。
2) 相关长度
相关函数是对随机表面上任意两点间的相关程度的描述, 海面的自相关函数定义为
| $ C\left(s^{\prime}\right)=\left\langle h(s) h\left(s+s^{\prime}\right)\right\rangle . $ | (1) |
海面自相关函数是s处的高度h(s)与另一点s+s′处的高度h(s+s′)之间相似性的一种度量方式。归一化自相关函数可以得到相关系数
| $ \rho\left(s^{\prime}\right)=\frac{C\left(s^{\prime}\right)}{\sigma_h^2}=\frac{\left\langle h(s) h\left(s+s^{\prime}\right)>\right.}{\sigma_h^2}, $ | (2) |
其中: σh2为海面的均方波高;相关系数ρ(s′)是海浪谱ξ(ω)的逆傅里叶变换:
| $ \rho\left(s^{\prime}\right)=\frac{1}{2 \pi \sigma_h^2} \int\limits_{-\infty}^{\infty} \xi(\omega) \mathrm{e}^{\mathrm{j} \omega s^{\prime}} \mathrm{d} \omega . $ | (3) |
表面相关长度lcor定义为ρ(s′)=1/e时s′的值[12]。其物理意义是, 如果表面上的两点在水平方向上的间距大于该值, 那么这两个点的高度值从统计意义上来讲是近似独立的。当该表面为一光滑平面时, 相关长度lcor→∞, 表明此时表面上每一点与其他各个点均相关。
1.2 菲涅尔反射系数菲涅尔反射是对入射波在两种介质中因折射系数不同而引起的波的反射的现象的描述, 其计算公式为
| $ \begin{aligned} & \varGamma_{\mathrm{V}}=\frac{\varepsilon_{\mathrm{s}} \sin \alpha-\sqrt{\varepsilon_{\mathrm{s}}-\cos ^2 \alpha}}{\varepsilon_{\mathrm{s}} \sin \alpha+\sqrt{\varepsilon_{\mathrm{s}}-\cos ^2 \alpha}}, \\ & \varGamma_{\mathrm{H}}=\frac{\sin \alpha-\sqrt{\varepsilon_{\mathrm{s}}-\cos ^2 \alpha}}{\sin \alpha+\sqrt{\varepsilon_{\mathrm{s}}-\cos ^2 \alpha}} . \end{aligned} $ | (4) |
其中:ΓV是垂直极化的菲涅尔反射系数, ΓH是水平极化的菲涅尔反射系数, α是无线电波的入射掠射角, εs是海水介电常数。
1.3 镜面反射系数文献[13]中采用零阶贝塞尔函数I0(PS)来修正镜面反射系数ρs, 并通过与实测得到的数据相对比, 证明其更适用于海面情况:
| $ \rho_{\mathrm{s}}=\exp \left[-P_{\mathrm{s}}\right] \mathrm{I}_0\left(P_{\mathrm{s}}\right), $ | (5) |
| $ P_{\mathrm{s}}=2\left(\frac{2 \pi \sigma_h \sin \alpha}{\lambda}\right)^2, $ | (6) |
其中:σh为海面均方根波高, α是入射波掠射角, λ为波长。
在实际的星船海洋通信场景中, 卫星覆盖范围广, 镜面反射系数受地球曲率的影响不能被忽略, 因此需要用地球曲率因子D对其进行修正[14]:
| $ \rho^{\prime}{ }_{\mathrm{s}}=\rho_{\mathrm{s}} D\\ =\rho_{\mathrm{s}}\left(1+\frac{2 R_1 R_2}{R_{\mathrm{e}}\left(R_1+R_2\right) \sin \alpha}\right)^{-\frac{1}{2}} . $ | (7) |
相对应的漫反射系数表示为
| $ \rho_{\mathrm{d}}=\sqrt{1-\rho_{\mathrm{s}}^{\prime 2}} . $ | (8) |
其中:R1表示从卫星发射端到镜面反射点的距离, R2则表示从镜面反射点到船站接收端的距离, Re则为地球的半径。
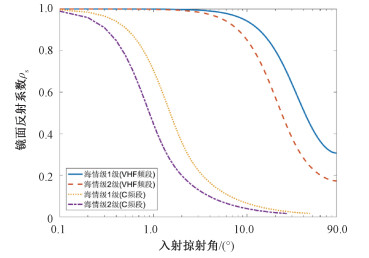
在不同频段、不同海情级下的镜面反射系数和入射掠射角的关系如图 1所示。
|
Download:
|
| 图 1 不同频段下镜面反射系数与入射掠射角 Fig. 1 Specular reflection coefficient and incidence grazing angle at different frequency bands | |
图 1表明随着入射掠射角的增大, 镜面反射系数逐渐减小;在相同入射掠射角条件下, 海情级升高, 镜面反射系数也会下降;VHF频段相较于C频段(4~8 GHz)镜面反射系数更大。例如掠射角为10°, 海情级1级时VHF频段的镜面反射系数约为C频段镜面反射系数的30倍, 这导致海面镜面反射对于海上多径衰落信道影响更为明显。
2 星船信道模型 2.1 基于球坐标系的星船传播几何模型以地心为原点, 船站的接收机方向为z轴方向, 根据船站、卫星端和镜面反射点之间的几何关系, 建立星船散射球坐标系。如图 2所示。

|
Download:
|
| 图 2 星船散射几何模型 Fig. 2 Geometric model of Satellite-Ship scattering | |
图 2中, S点为卫星位置, R点为船站接收机位置, P点为镜面反射点, α为镜面反射点偏角, β为仰角, θ为卫星的地心角。在上述坐标系中, 根据几何关系可知上述各点坐标R(Re+hr, 0, 0), S(Re+hs, θ,
海面信道的多径模型包括视距分量、镜面反射分量和漫反射分量。镜面反射分量是指信号只经过一次镜面反射的路径上的信号分量;漫反射分量则是指经海面漫反射的多条路径上的信号分量。
2.2.1 多径信道基本模型VDE-SAT信号最主要的传播方式为视距传播, 即发射端发射的信号按照单一的传播路径进行传播。自由空间中的传播损耗可以看作是整个系统中最主要的损耗, 其损耗可以根据自由空间传播路径进行计算[15], 自由空间传输损耗采用分贝形式表示为:
| $ L_{\mathrm{s}}=20 \lg (4 \pi)+20 \lg d+20 \lg f-20 \lg c, $ | (9) |
其中: d表示星船收发两端天线之间的距离, f为无线电波的频率, c为光速。
由于无线信号易受海面传播环境的影响, 在传播路径上产生了反射, 当电波传输到接收端的天线时, 接收信号并不是从单一路径来的, 而是许多条路径的多个信号的叠加[16]。假设发送信号为
| $ s(t)=\operatorname{Re}\left\{b(t) \exp \left(\mathrm{j} 2 \pi f_{\mathrm{c}} t\right)\right\}, $ | (10) |
其中: fc为载波频率, b(t)为基带信号。此信号经过多径信道时受到多径效应的影响, 接收信号可表示为
| $ R(t)=\operatorname{Re}\left\{r(t) \exp \left(\mathrm{j} 2 \pi f_{\mathrm{c}} t\right)\right\}, $ | (11) |
其中r(t)为接收信号的复数形式
| $ r(t)=\sum\limits_i \alpha_i b\left(t-\tau_i\right) \exp \left(-\mathrm{j} 2 \pi f_{\mathrm{c}} \tau_i\right), $ | (12) |
其中: αi为第i条路径的衰减因子,
| $ \begin{aligned} r(t)= & \sum\limits_i \alpha_i b\left(t-\tau_i\right) \exp \left[-\mathrm{j}\left(2 \pi f_{\mathrm{c}} \tau_i-\right.\right. \\ & \left.\left.2 \pi f_{\mathrm{m}} t \cos \theta_i\right)\right], \end{aligned} $ | (13) |
其中:fm为最大多普勒频移, θi为第i条路径上的信号的到达方向和接收终端运动方向之间的夹角。式(13)表明了多普勒频移和多径效应对原始的传输信号b(t)的影响。
2.2.2 有效漫反射区域计算在镜面反射点附近, 经过一定倾斜的反射面反射的无线电波, 部分可以被接收端接收, 这些能够被接收端接收的电波的反射面组成的区域被称作有效漫反射区[17]。接收信号的幅值和时延由漫反射区域的范围和位置确定。有效漫反射区的范围如图 3所示。

|
Download:
|
| 图 3 有效漫反射区域 Fig. 3 Effective diffuse area range | |
有效漫反射区内的反射平面要有一定的倾斜角度, 其倾斜的角度用β表示。越靠近镜面反射点, β的值就越接近零。设S(xa, 0, za)为有效漫反射区内的任意一点, Hr为船站接收端接收机的高度, Ht为卫星端发射机的高度, R1为漫反射点到船站接收端的距离, R2为漫反射点到卫星发射端的距离, R为船站接收端到卫星发射端的直线距离, G为两者之间x轴的轴向距离。β是从漫反射点S到卫星发射端的单位向量U2与漫反射点到船站接收端的单位向量U1的和向量UB与海面的法向量 j的夹角。上述关系表示为:
| $ \boldsymbol{U}_1=\left(-x_a i+H_{\mathrm{r}} j-z_a k\right) / R_1, $ | (14) |
| $ \boldsymbol{U}_2=\left(\left(G-x_a\right) i+H_{\mathrm{t}} j-z_a k\right) / R_2, $ | (15) |
| $ \boldsymbol{U}_{\mathrm{B}}=\left(\boldsymbol{U}_1+\boldsymbol{U}_2\right) /\left|\boldsymbol{U}_1+\boldsymbol{U}_2\right|, $ | (16) |
| $ \beta=\arccos \left(\boldsymbol{U}_{\mathrm{B}} \cdot \boldsymbol{j}\right) . $ | (17) |
假设β的分布服从高斯分布[18], 定义β0为在任意小的漫反射区上的海面斜率的均方根[14]
| $ \beta_0=\frac{2 \sigma_h}{l_{\text {cor }}}, $ | (18) |
其中:σh为均方根波高, lcor为海面两点间波高的相关长度。由式(18)可知β0随着海情级而改变。有效漫反射区的边界的确定由下式[19]决定
| $ \beta_{\lim }=\frac{k \beta_0}{\sqrt{2}}, $ | (19) |
其中, k为标准方差的系数, 本文取k=3。
根据上述星船散射几何模型, 有效漫反射区应限定在接收端无线视距传播区域内。设收发天线的高度分别为20 m和330 km, 海情级1级和4级的情况下的β0分别为0.02、0.05, 联立式(14)~式(19), 根据上述求解有效漫反射区域范围的方法, 求出有效漫反射区域位置和范围, 利用MATLAB仿真星船模型中有效漫反射区域的示意图,如图 4所示。

|
Download:
|
| 图 4 有效漫反射区域范围仿真示意图 Fig. 4 Schematic diagram of effective diffuse reflection area range simulation | |
在上述有效漫反射区内求出到达接收端的镜面反射能量和漫反射能量, 根据2.2.1节描述的多径信道的基本模型, 将入射信号进行叠加, 即可形成多径衰落信道。
1) 镜面反射能量
镜面反射能量分量相对直射径能量分量的比值计算公式如下
| $ \frac{v_{\mathrm{Spe}}}{v_{\text {Dir }}}=\rho_{\mathrm{s}} \sqrt{G_{\mathrm{ant}}}\left|\varGamma_{\mathrm{v}}\right|, $ | (20) |
其中:ρs为镜面反射系数, Γv为菲涅尔反射系数, Gant是海面镜面反射点到接收端接收机方向的天线增益与沿着直射径到接收端接收机方向上的天线增益的功率比值。
2) 漫反射能量
接收信号中的漫反射能量分量可以看作是经过有效漫反射区内一任意小块面积dS反射后的能量分量的集合[19]。dS的形状和大小的选取对所构建的多径模型的结果影响较大, 因此应保证在选取过程中任意小块面积dS里面的各个散射点的信号时延差尽可能相近。本文选取的dS为窄带长条状[18]。漫反射能量分量和直达路径能量分量的比值计算公式如下
| $ \begin{aligned} & \frac{v_{\text {Dif }}}{v_{\text {Dir }}}= \sqrt{\frac{1}{4 \pi}\left(\frac{R}{R_1 R_2}\right)^2 \frac{1}{\beta_0^2} \exp \left(-\frac{\beta^2}{\beta_0^2}\right) d S} \cdot \\ &\;\;\;\;\;\;\;\;\;\;\;\;\left|\varGamma_{\mathrm{V}}\right| \cdot \sqrt{G_{\text {ant }}} \cdot \rho_{\mathrm{r}} \cdot \sqrt{S_f}, \end{aligned} $ | (21) |
其中:R、R1、R2分别表示直达路径长度、发射端到漫反射点的距离、漫反射点到接收端的距离;ρr为粗糙因子系数, 是镜面反射系数ρs的函数, 计算公式如下
| $ \rho_{\mathrm{r}}=\sqrt[4]{\left(1-\rho_{\mathrm{s}}^2\left(\alpha_1\right)\right) \cdot\left(1-\rho_{\mathrm{s}}^2\left(\alpha_2\right)\right)}, $ | (22) |
其中:α1表示无线电波的入射掠射角;α2表示无线电波反射掠射角;
根据式(11)~式(13), 将信号的视距分量、镜面反射分量和漫反射分量进行叠加, 即可构建起VDE-SAT星船下行链路信道模型。
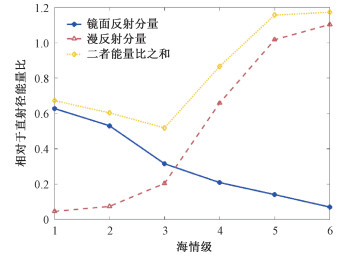
3 仿真结果与分析根据2.2.3节中对海上多径信道镜面反射分量和漫反射分量的研究,可以得到镜面反射和漫反射分量与直射径分量的能量比以及二者能量比之和在不同海情级条件下变化趋势,如图 5所示。
|
Download:
|
| 图 5 不同海情级下的镜面反射、漫反射分量和直射径分量的能量比 Fig. 5 The energy ratio of specular reflection, diffuse reflection component and direct diameter component under different sea conditions | |
图 5表明,在海情级小于3级时镜面反射能力大于漫反射能量,二者的能量和逐渐降低;在海情级大于3级时,漫反射能量大于镜面反射能量,二者的能量和逐渐升高。
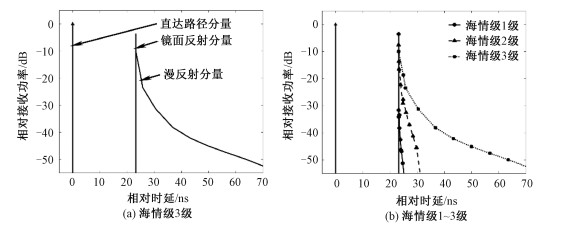
为了进一步说明镜面反射和漫反射分量对信道的影响,通过MATLAB仿真得到不同海况下海上多径信道的功率时延分布谱(power-delay profile, PDP),如图 6所示,其中纵轴表示相对于直射信号的接收信号功率,横轴则表示相对于直达路径的信号时延。
|
Download:
|
| 图 6 海上多径信道功率时延分布谱 Fig. 6 Power delay distribution spectrum of Marine multipath channels | |
图 6(a)表明,在VDE-SAT多径模型中当前海况下漫反射分量相较于镜面反射分量功率低,漫反射多径时延远大于镜面反射时延。随着时延的增大,漫反射多径分量的功率逐渐减小。
图 6(b)表明,随着海情级的增大,海面漫反射多径分量的时延扩展增大,即漫反射的多径时延增加,漫反射分量的功率增大。
综上所述,在海况较好时,多径信道以镜面反射为主;海况较差时,多径信道以漫反射为主。值得注意的是,ITU-R的M.2435[20]数据研究报告中指出VDE-SAT信道衰落机制主要为海面镜面反射;文献[21]在描述海上通信环境时,也指出对于平静的海面,较强的反射路径将占主导地位。本文的仿真结果与上述结论相吻合,验证了本文信道模型的准确性。
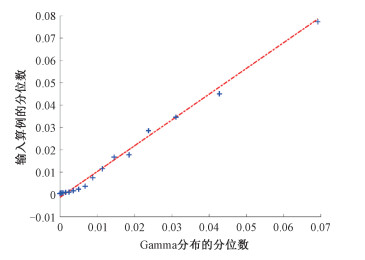
在接收机高度为20 m,通信仰角为10°,海情级2级条件下对所构建多径信道功率的概率分布进行拟合,并与Gamma分布作分位数-分位数图(quantile-quantile plots,QQ plot)如图 7所示。
|
Download:
|
| 图 7 信道衰落和Gamma分布的分位数-分位数图 Fig. 7 QQ plot of channel fading and Gamma distribution | |
图 7中样本数据点的分布几近一条直线,表明样本数据较好地符合Gamma分布。值得注意的是,这与文献[10]中利用VDE卫星实验数据得出的Gamma分布拥有着最佳拟合的结论相吻合,验证了本文多径信道模型的准确性。考虑误差原因在于,文献[10]对NorSat-2卫星持续3周的观测,接收机高度固定为20 m,通信仰角为5°~60°,将捕获到的数据取平均值处理后拟合。这和本文所采用的接收机高度、通信仰角等参数不同,也未能像本文一样考虑不同海情级,根据不同的海浪波高进行信道建模。
以前面的分析和模型为基础, 在不同海情级场景下, 对星船下行链路进行了Turbo编码和卷积码编码误码率BER的仿真工作, 并将仿真结果同已有参考文献给出的结论进行对比,来验证本文建模方法的准确性和有效性。
根据Douglas的海情级划分,在海情级为6级时,海面波高约为5 m,海况极度恶劣,普通渔船已不能出海进行捕捞作业,因此该场景较少进行研究分析。在文中也只针对海情级1~5级进行误码率仿真工作。仿真参数如表 2所示, 采用Eb/N0-BER来衡量通信系统的性能。
|
|
表 2 误码率仿真参数设置 Table 2 BER simulation parameter setting |
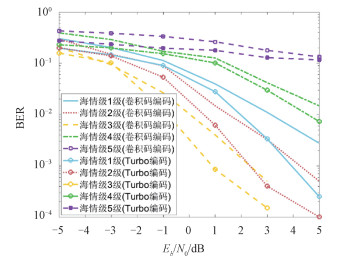
假设接收时接收机和直射分量完全同步, 海情级1~5级条件下, 通信链路在不同信道编码方式下的误码率曲线如图 8所示。其中, 仿真采用(2, 1, 3)传统卷积码, 约束长度为3, 码率为1/2, 译码算法为Viterbi译码算法;采用生成矩阵(7, 5)的Turbo码, 码率为1/2, 译码算法为Log-MAP算法, 迭代次数5次。
|
Download:
|
| 图 8 星船下行链路误码率曲线 Fig. 8 BER curve of Satellite-Ship downlink | |
图 8表明,海情级1~3级时,误码率随着海情级升高而降低;海情级4~5级时误码率随着海情级升高而升高。考虑其原因在于,海情级1~3级时,多径信道以镜面反射为主,由于多径的时延扩展,在接收端造成了严重的码间串扰,对应着较高的误码率。随着海情级的升高,信道质量有所改善,对应着较低的误码率;海情级4~5级时,多径信道以漫反射为主,信号衰落增大使通信链路性能变差,误码率急剧升高。
此外, 图 8还表明, 在同一海情级和Eb/N0的条件下, 采用Turbo码编码的通信链路误码率性能要明显优于采用卷积码编码的通信链路, 其抗多径衰落效果更好。考虑其原因在于,Turbo码的并行级联结构, 巧妙地将分量码和交织器进行结合, 实现了随机编码, 从而达到了接近香农极限的性能。应当指出,上述仿真结果也与ITU-R M.2092-0[22]协议中关于FEC算法使用Turbo信道编码的规定相吻合,验证了本文信道模型的准确性。
综上所述,通过对所构建信道的PDP谱、QQ plot图、VDE-SAT下行链路的信号误码率3个方面的仿真分析验证了本文提出的VDE-SAT下行链路信道建模方法的准确性和有效性。
4 总结本文提出一种基于球坐标系的VDE-SAT下行链路信道建模方法,充分考虑了地球曲率和海面海浪因素对于信号传播路径的影响,在缺少实验数据情况时仍能准确地对VDE-SAT下行链路信道建模,并给出了不同海情级下的多径信道延迟功率谱图。最后基于此信道模型, 设置合理参数在多种海情级下对星船下行通信链路误码率进行MATLAB仿真。仿真结果与现有文献的结论相吻合,验证了本文建模方法的准确性。
仿真结果表明,ITU-R M.2092-0协议里规定的Turbo编码相较于传统的卷积码有一定的抗多径能力;VDE-SAT下行链路多径衰落信道模型在低海情级下以镜面反射为主,高海情级下以漫反射为主。本文成果还可以为VDE-SAT船载终端接收机的捕获算法的设计提供理论支撑, 为后续VDES系统设计方案的策划和制定提供重要的理论支持。
| [1] |
熊雅颖. 海事通信技术新进展: VDES系统[J]. 卫星应用, 2016(2): 35-40. |
| [2] |
Luglio M, Roseti C, Zampognaro F. VDES performance evaluation for future e-navigation services[C]//Proceedings of the 15th International Joint Conference on e-Business and Telecommunications. July 26-28, 2018. Porto, Portugal. SCITEPRESS-Science and Technology Publications, 2018: 67-75. DOI: 10.5220/0006850200670075.
|
| [3] |
IALA. Guideline G1139 The technical specification of VDES[S/OL]. (2019-06-21)[2022-02-16]. https://www.iala-aism.org/product/g1139-technical-specification-vdes/.
|
| [4] |
夏明华, 朱又敏, 陈二虎, 等. 海洋通信的发展现状与时代挑战[J]. 中国科学(信息科学), 2017, 47(6): 677-695. Doi:10.1360/N112017-00016 |
| [5] |
Corazza G E, Vatalaro F. A statistical model for land mobile satellite channels and its application to nongeostationary orbit systems[J]. IEEE Transactions on Vehicular Technology, 1994, 43(3): 738-742. Doi:10.1109/25.312773 |
| [6] |
邵立杰. AIS海上电波传播模型研究[D]. 辽宁大连: 大连海事大学, 2014.
|
| [7] |
刘媛美. VDES信道建模技术研究[D]. 南京: 东南大学, 2019.
|
| [8] |
Ma S X, Shi K, Meng X, et al. Frequency offset estimation algorithm of VDES signals based on cross-correlation[C]//2018 IEEE 4th International Conference on Computer and Communications. December 7-10, 2018, Chengdu, China. IEEE, 2018: 1234-1238. DOI: 10.1109/CompComm.2018.8780774.
|
| [9] |
Zheng B X, Yen K, Peng X M, et al. Angle partition-based TDMA for VDES satellite multiuser downlink communications[C]//GLOBECOM 2020-2020 IEEE Global Communications Conference. December 7-11, 2020, Taipei, Taiwan, China. IEEE, 2020: 1-6. DOI: 10.1109/GLOBECOM42002.2020.9322170.
|
| [10] |
Giambene G, Gomez I, de Cola T, et al. Satellite forward VDES channel modeling and impact on higher-layer performance[J]. International Journal of Satellite Communications and Networking, 2021, 1-20. Doi:10.1002/sat.1430 |
| [11] |
Bråten L E, Eriksen T, Skauen A N, et al. On the VHF radio channel for the data exchange system via satellite (VDE-SAT): experimental results from the NorSat-2 satellite experiment[C]//36th International Communications Satellite Systems Conference(ICSSC 2018). October 15-18, 2018, Niagara Falls, ON, Canada. IET, 2018: 1-8. DOI: 10.1049/cp.2018.1705.
|
| [12] |
白伟华. GNSS-R海洋遥感技术研究[D]. 北京: 中国科学院研究生院(空间科学与应用研究中心), 2008.
|
| [13] |
Beard C. Coherent and incoherent scattering of microwaves from the ocean[J]. IRE Transactions on Antennas and Propagation, 1961, 9(5): 470-483. Doi:10.1109/TAP.1961.1145043 |
| [14] |
Barrick D. Rough surface scattering based on the specular point theory[J]. IEEE Transactions on Antennas and Propagation, 1968, 16(4): 449-454. Doi:10.1109/TAP.1968.1139220 |
| [15] |
吴海龙. 卫星移动通信衰落信道的建模与仿真研究[D]. 哈尔滨: 哈尔滨工程大学, 2015.
|
| [16] |
沙学军, 吴宣利, 何晨光. 移动通信原理、技术与系统[M]. 北京: 电子工业出版社, 2013.
|
| [17] |
杨伟. 三维复杂粗糙海面电磁散射建模研究与特性分析[D]. 成都: 电子科技大学, 2012.
|
| [18] |
黄芳. 海上无线电波传播特性与信道建模研究[D]. 海口: 海南大学, 2015.
|
| [19] |
Haspert K, Tuley M. Comparison of predicted and measured multipath impulse responses[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(3): 1696-1709. Doi:10.1109/TAES.2011.5937259 |
| [20] |
ITU-R. Report ITU-R M. 2435-0-Technical studies on the satellite component of the VHF data exchange system[S/OL]. (2019-05-27)[2022-02-16]. https://www.itu.int/dms_pub/itu-r/opb/rep/R-REP-M.2435-2018-PDF-E.pdf.
|
| [21] |
Wang J, Zhou H F, Li Y, et al. Wireless channel models for maritime communications[J]. IEEE Access, 2018, 6: 68070-68088. Doi:10.1109/ACCESS.2018.2879902 |
| [22] |
ITU-R. Recommendation ITU-R M. 2092-0 Technical characteristics for a VHF data exchange system in the VHF maritime mobile band[S/OL]. (2015-10)[2022-02-16]. https://www.itu.int/rec/R-REC-M.2092.
|
 2024, Vol. 41
2024, Vol. 41 


