2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
风场的垂直分布是气象、空气动力学、风工程等领域的重要研究内容,通常可用风切变指数表征其差异大小。地面热力状况的日变化会对边界层风场产生影响,对于风切变的产生、维持、发展至关重要,例如,风切变指数不仅对风电场的发电量有较大影响而且对风机安全也有显著影响。当前风力发电机的叶轮直径已超过140 m,未来风机的叶轮直径会超过250 m[1]。较大的风切变会在叶轮上产生较强的不平衡气动载荷,会对风机的安全性造成影响,严重时甚至会导致风机倾覆。同时,风切变指数的大小,也会对风电场的发电量有较大影响[2]。风切变的探测和研究具有重要实际价值。
低空风切变(low-level wind shear)是指600 m以下风向或风速在水平或垂直方向的突然变化[3-4]。风切变往往还具有持续时间短、空间尺度小、出现突然等特点,较难被常规气象设备捕捉到[3, 5]。测风塔是观测大气风场的常用方式,其数据质量和可信度均较高。但是,测风塔的最大测量高度受到较大限制,测量的高度层数目也有限。激光雷达具有较好的时空分辨率和测量高度,可在一定程度上弥补测风塔测量高度的不足。
激光雷达基于大气气溶胶粒子的多普勒效应测量风速[6]。激光雷达的激光束以设定的扫描圆锥角向上扫描,通过内置风速算法反演大气风速,可以测量40~200 m高度风速廓线,垂直分辨率为20 m(可调),测量范围还可扩展到400 m高度,设计测量精度达0.2 m·s-1,1~2 s可更新风廓线的测量结果[7]。激光雷达是一种遥感设备,以一定的圆锥角向上扫描,在140 m高度处,测量区域的范围可达到74 m,在激光雷达风速算法中会采用一定假设:在测量区域内风场要相同,具有均一性,因此,激光雷达的使用需要首先验证其适用性。通常激光雷达对于风速风向的测量较为准确,但是当前激光雷达在测量风切变方面的验证与研究还不足,尤其是对风切变发生原因的研究更为不足。
风切变指数受到大气稳定度的影响,大气越稳定,风切变指数越大[8]。稳定状态下的风切变指数为高值,是因为垂直动量传输受到限制[9-10]。国内外众多学者对稳定度分类问题做了许多研究工作,提出十几种稳定度分类方法[11]。根据使用资料的不同大气稳定度分类方法主要分为常规气象资料法和特殊气象资料法两大类,特殊气象资料法又可分为梯度资料分类法和湍流资料分类法:1)常规气象资料法有Pasquill法、Pasquill-Turner法、P·S法、城市稳定度分类法;2)梯度资料分类法有温度梯度法、温度梯度-风速法、风速比法、理查森数(Ri)法、总体理查森数(BRi)法; 3)湍流资料分类法有风向脉动标准差法、莫宁-奥布霍夫长度法[12-15]。由气象塔梯度资料确定大气稳定度的方法,通常有Ri法、温度梯度法、位温梯度-风速法、风速比较法等[16-18]。常规气象资料法,主要采用地面观测数据,对于边界层垂直方向的观测不足;湍流资料分类法,需要精准的风速、湍流脉动测量[19-21],需要采用更为专业的设备。本文对大气稳定度的计算,采用梯度资料分析法中的温度梯度法、BRi法,利用平坦地形下140 m的测风塔的温度、风速计算大气稳定度参数,可以很好地捕捉大气在垂直高度上的梯度信息,同时选用设备和计算方法也相对较为容易应用到相关领域。
本文通过测风塔和激光雷达的同期外场测量,验证激光雷达对低空风切变的测量精度,同时研究大气稳定度对于风速切变和风向切变的影响。
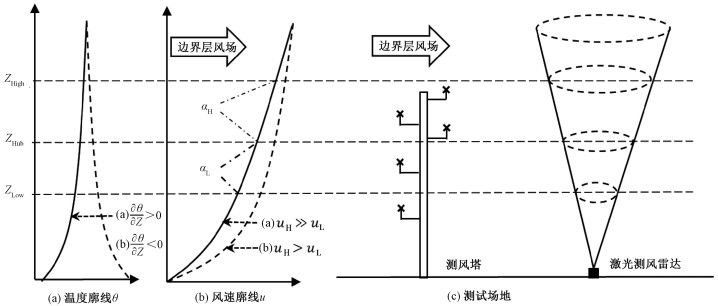
1 设备与观测 1.1 风速温度的垂直分布和观测低空风切变反映了低层大气的动力学特征,可由垂直风廓线计算;大气稳定度也可由垂直温度廓线获得,通过垂直梯度方法得到的风切变与大气稳定度具有更好的空间匹配度。多个高度上的垂直梯度观测在环境科学、风能利用、风工程等应用领域也更直观、更容易开展。图 1是垂直廓线的分布与观测的示意图,图 1(a)和1(b)是温度和风速廓线,实线表示温度层结稳定时,虚线表示温度层结不稳定时。图 1(c)是测试场地示意图,测试场地包含了140 m测风塔和激光测风雷达。在实际应用中超过100 m测风塔的建设较难,因此激光雷达是风廓线的有效测量方式,同时激光测风雷达也可验证测风塔的垂直观测,尤其是测风塔不同高度风向在安装时可能存在一定的角度偏差,激光雷达可以检验风向测量的一致性。
|
Download:
|
| 图 1 大气温度和风速廓线分布图和测量示意图 Fig. 1 The vertical distribution of temperature, wind speed profile and measurement diagram | |
湍流可以加速边界层大气的垂直混合,夏季白天是典型的温度层结不稳定场景,大气湍流运动向上输送热通量[22];夜间通常温度层结稳定,其效果是向下输送热通量。由于近地面层中平均风速总是随高度增加,因此动量通量总体效果是向下输送[22],风切变在夜间常常大于白天,夜间动量通量向下输送要弱于白天。本文选用测试场地内较高测风塔和激光测风雷达数据,研究大气稳定度对风切变的影响。
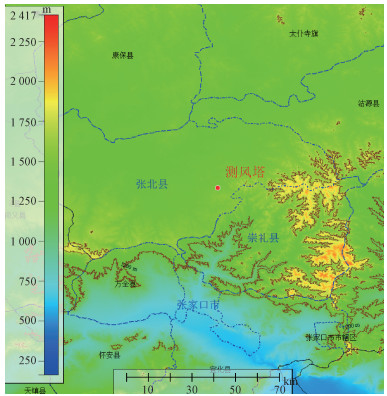
1.2 测试场地激光测风雷达的测试场地位于河北省张家口市,地理位置和主风向如图 2所示。分布图的水平范围约为100 km,位于张北县、崇礼县交界区域的坝上草原地区。图中颜色代表地形海拔高度,对于左侧垂直色标的数值,图中蓝色虚线是测试场地周边的区县级行政区界限,棕色实线是1 200、1 700 m高度的等高线,两高度之间的地形色标基本为绿色。坝上地区整体风能资源较好,测试场地周边地形较为平坦,适合作为遥感类测风设备的测试场地。测风塔海拔1 452 m,测风塔周边1 km范围内地形起伏不超过80 m。场地周边植被分布以草地为主,无高大树木,测试场地满足IEC 61400-12-1标准中平坦地形的规定[23],可排除地形因素引起的测量误差。
|
Download:
|
| 图 2 测试场地的地理分布图 Fig. 2 The geographical location map of the test site | |
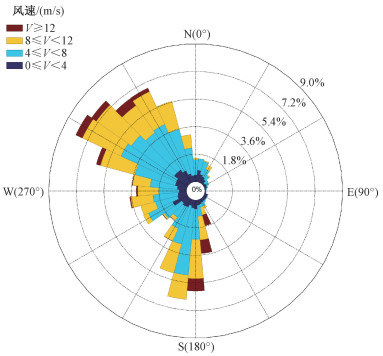
图 3是场地的风玫瑰图,主导风向为西北风,其次是南风风向。风速分布以4~8、8~12 m·s-1这2个风速区间为主,小于4 m·s-1或者大于12 m·s-1的时间较少。
|
Download:
|
| 图 3 测试场地的风玫瑰图 Fig. 3 Wind rose | |
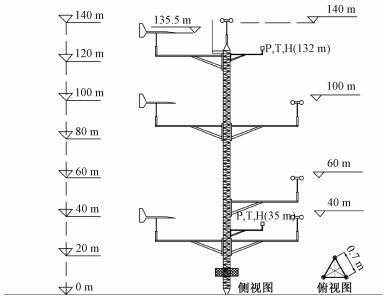
图 4为测风塔示意图,测风塔的高度为140 m,一共安装4个风速仪和3个风向标,风速仪和风向标在安装前经过实验室标定。当地主导风向为西北风,风速仪安装在测风塔的东北、西南方向,尽量减少塔体对风速测量的影响。测风塔保存10 min平均数据,测量期间测风塔设备运行正常,风速风向的数据质量较好。
|
Download:
|
| 图 4 选用测风塔的风速、风向、温度等气象要素测量高度的示意图 Fig. 4 Schematic diagram of the measurement height of wind speed, wind direction and temperature | |
激光测风雷达通过气溶胶的多普勒效应测量风速,本次测试选用激光测风雷达型号为WindCube V2.0,该激光测风雷达依次发射5个方向的激光束,切换时间为1 s,前4束激光束方位角分别为0°、90°、180°、270°,高度角均为28°,第5激光束为垂直向上,测量高度与测风塔一致,详细参数见表 1。由于测量时间基本为冬季,132和35 m的温度在夜间较为接近,不能完全反映大气层结稳定的状况,垂直温度梯度利用激光测风雷达在1 m高度上的温度数据,通过132和1 m这2层温度计算。
|
|
表 1 测风塔和激光测风雷达测量要素高度 Table 1 The height of measured variables of Met Mast and Lidar |
大气静力稳定度是层结大气对垂直扰动的抑制或促进作用,即空气气团受到动力因子或热力因子的扰动后其垂直运动能否继续发展[22]。位温的垂直梯度是大气的静力稳定度的判据之一[24]。位温垂直梯度是温度和气压的函数[22], 可由2个不同高度层上位温通过下式直接计算
| $ \theta=T\left(\frac{p_0}{p}\right)^\kappa . $ | (1) |
由于大气通常满足静力平衡条件,式(1)可以简化为下式,主要变量是温度垂直递减率[15, 24-25]。
| $ \frac{\partial \theta}{\partial z} \approx \frac{\theta}{T}\left(\frac{\partial T}{\partial z}+\gamma_{\mathrm{d}}\right). $ | (2) |
其中: P0是标准气压,常取1 013.25 hPa;T是温度;P是大气气压;κ是常数,为0.286;γd是干绝热递减率,为9.8 K/km。
大气的静力稳定度是浮力对流的一种量度,静止大气的稳定度与风无关,大气湍流状态的维持既有热力原因,也有动力原因[22]。Ri是综合考虑了湍流热力因子和动力因子作用的稳定度参数,在风速测量精度一般的情况下,常用BRi代替梯度Ri[11],可以减少通量Ri计算时对2层风速差值测量精度的需求。BRi通过2个高度上的位温和风速计算,无需动用湍流脉动测量仪器[11, 22, 26]。
| $ B R i=\frac{\mathrm{g}}{\bar{\theta}} \cdot \frac{\partial \bar{\theta}}{\partial z} \cdot \frac{\overline{z^2}}{\overline{u^2}} \approx \frac{g}{\bar{\theta}} \cdot \frac{\Delta \bar{\theta}}{\Delta z} \cdot \frac{\left(\sqrt{z_1 z_2}\right)^2}{\left(\sqrt{V_1 V_2}\right)^2}. $ | (3) |
当BRi>0时,浮力做功使湍流能量减弱,此时温度层结稳定;当BRi<0时,浮力做功使湍流能量增强,此时温度层结不稳定;当BRi=0时,大气层结是中性的,浮力做功对湍流能量的影响较小[22]。
将式(2)引入式(3)可以得到位温梯度的计算公式,包含位温、大气温度、温度梯度,温度、气压各自对大气稳定的影响较小:
| $ \frac{\partial \theta}{\partial z}=\left(\frac{P_0}{P}\right)^{0.286}\left(\frac{\partial T}{\partial z}+\gamma_{\mathrm{d}}\right) \approx\left(\frac{P_0}{\bar{P}}\right)^{0.286}\left(\frac{\partial T}{\partial z}+\gamma_{\mathrm{d}}\right) . $ | (4) |
式(4)含有两部分,分别由气压和温度梯度决定,气压变化通常较小,测试期间气压的变化范围为830~870 hPa,(P0/P)0.286的数值范围为1.040 6~1.054 7,变化幅度为1.4%,因此可采用测试期间的平均气压进行计算,本项可视为大气静力稳定度的修正因子。
将式(2)引入式(4)可以得出BRi的计算公式,可由上下2层的平均温度、温度差值、风速、高度计算:
| $ BRi =\frac{2 \mathrm{~g}}{T_1+T_2} \cdot\left(\frac{T_2-T_1}{z_2-z_1}+\gamma_{\mathrm{d}}\right) \cdot \frac{\left(\sqrt{z_1 z_2}\right)^2}{\left(\sqrt{V_1 V_2}\right)^2} \text {. } $ | (5) |
垂直风切变包含风速和风向在垂直方向的变化,风速切变指数Shear和风向切变指数Veer可由下面公式[27]计算:
| $ \text { Shear }=\log \left(\frac{V_2}{V_1}\right) / \log \left(\frac{z_2}{z_1}\right)=\frac{\log \left(V_2\right)-\log \left(V_1\right)}{\log \left(z_2\right)-\log \left(z_1\right)} \text {, } $ | (6) |
| $ \text { Veer }=\frac{\operatorname{MOD}\left(D_2-D_1+180,360\right)-180}{z_2-z_1} . $ | (7) |
其中: z1、z2是2个不同的高度,V1、V2是2个高度对应的风速,D1、D2是对应的风向。
2.3 激光测风雷达的风速算法水平风速V和水平风向D,可用下式计算:
| $ u=\frac{V_{\mathrm{r} 0}-V_{\mathrm{r} 180}}{2 \sin \theta}, $ | (8) |
| $ v=\frac{V_{\mathrm{r} 90}-V_{\mathrm{r} 270}}{2 \sin \theta}, $ | (9) |
| $ V=\sqrt{u^2+v^2}, $ | (10) |
| $ D=\tan ^{-1} \frac{v}{u}, $ | (11) |
其中: u是经向风速,其正方向为从南向北;v是纬向风速,其正方向是从西向东;Vr0、Vr90、Vr180、Vr270为北、东、南、西4个方向上激光束的径向风速,气流流向激光测风雷达为正值;θ为激光束与垂直方向的夹角,数值为28°。
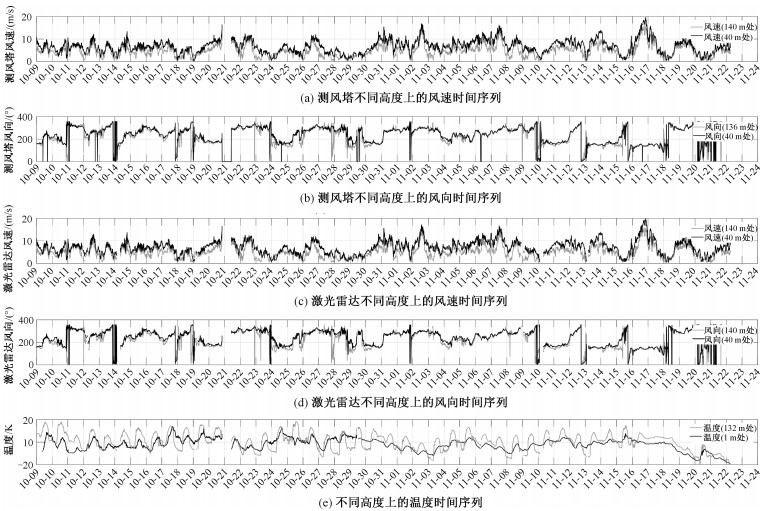
3 计算与分析 3.1 时间序列分布图本文对风切变、大气稳定度的计算,均采用2个高度(40, 140 m)处的风速、风向、温度计算,激光测风雷达和测风塔的原始数据时间序列分布如图 5。图 5(a)和5(b)为测风塔风速风向,图 5(c)和5(d)为激光测风雷达风速、风向,各图中黑线表示高层、灰线表示低层。4幅图中的黑线、灰线分别是140和40 m处风速风向数据,下文风速切变、风向切变由这2层数据计算。图 5(e)是132和1 m处温度,垂直温度梯度存在明显的日变化,白天的垂直温度梯度较小,大气较不稳定;夜间高层温度低于低层,大气较为稳定。原始数据的时间序列图表明激光测风雷达和测风塔的风速风向时间序列非常一致,采用的数据是可靠的。
|
Download:
|
| 图 5 激光测风雷达测量期间风速的时间序列 Fig. 5 Time series of wind speed during measurement campaign | |
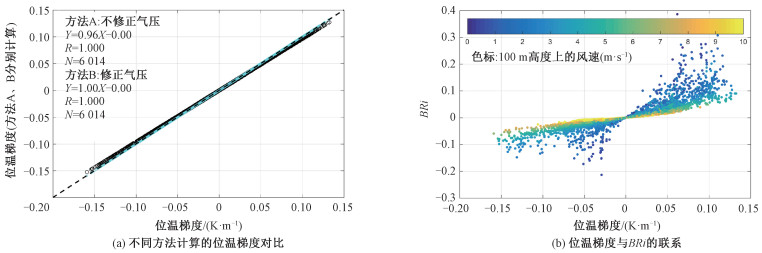
2.1节论述了位温梯度、BRi的计算方法,本小节通过本次观测中的实际数据,评估大气稳定度的计算方法。图 6(a)的X轴是2层位温直接计算出的位温梯度,Y轴是通过温度差值计算的位温梯度:浅蓝色散点利用测试期间的平均气压进行修正(方法B),黑色散点未进行气压修正(方法A),位温梯度可采用平均气压进行计算。图 6(b)是位温梯度与BRi的关系,两者通过风速可相互转化,本文侧重分析具体温度差异对风切变的影响,分析主要采用位温梯度作为大气稳定度参数。
|
Download:
|
| 图 6 位温梯度与BRi的联系 Fig. 6 Relation between the potential temperature gradient and BRi | |
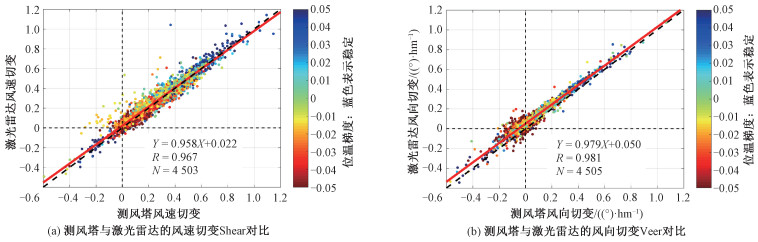
图 7是激光测风雷达和测风塔在不同高度上的风切变对比结果,图 7(a)是风速切变,7(b)是风向切变。风速切变和风向切变均采用40和140 m这2个高度的风速风向进行计算,散点是10 min平均数据分布,散点颜色表示位温的垂直梯度,黑色虚线是参考线,红色实线是二者的拟合关系。统计时采用风速大于2 m·s-1的数据,以降低微风带来的风切变计算误差,提高风切变的代表性。
|
Download:
|
| 图 7 激光测风雷达与测风塔的风切变对比结果 Fig. 7 Wind shear and veer comparison of Lidar and met mast | |
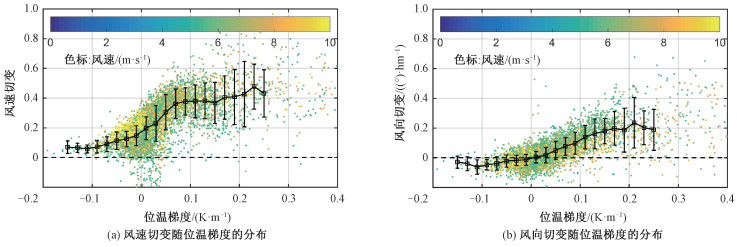
激光测风雷达对风切变的测量与测风塔具有一致性:风速切变的相关系数为0.967,拟合公式为Y=0.958X+0.022;激光测风雷达和测风塔的风向切变相关系数分别为0.981,拟合公式为Y=0.978X+0.050。图中散点颜色具有一定规律,风速切变、风向切变均与大气位温的垂直梯度关系密切,与大气层结状况关系紧密。在大气层结不稳定时,风速切变和风向切变均较小;在大气层结稳定时,风速切变和风向切变均较大。
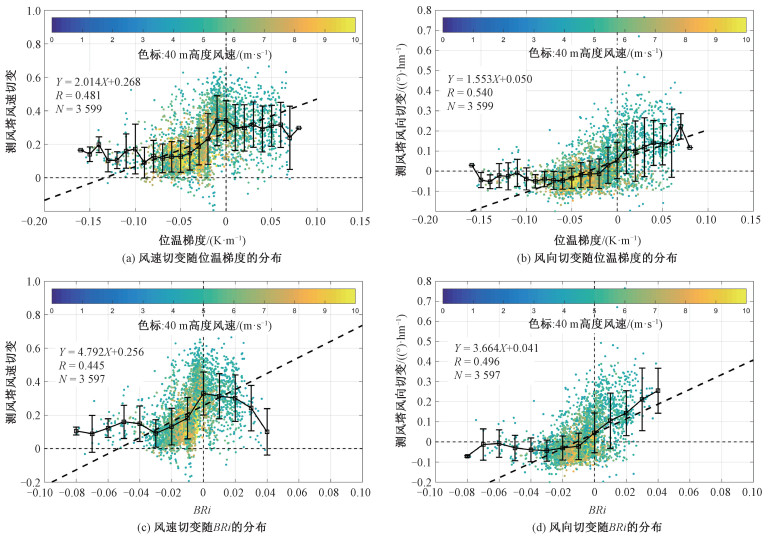
4 结果与讨论 4.1 大气稳定度对风切变的影响通过测风塔的垂直温度和风速廓线,可以分析大气稳定度对风切变的影响,结果如图 8所示。图 8(a)是位温垂直梯度与风速切变的联系,图 8(b)是BRi与大气稳定的联系。大气稳定度对风速、风向风切变影响显著,风速切变与位温的垂直梯度的相关系数为0.48,拟合关系为Y=2.01X+0.27。随着位温梯度的增加,风速切变有增加的趋势;当风速切变接近0.4时,风速切变随大气稳定度的增加保持不变;风速切变与位温梯度的相关性较好。
|
Download:
|
| 图 8 风速大于2 m·s-1时,大气稳定度对风速切变、风向切变的影响 Fig. 8 Impact on wind shear and wind veer by atmospheric stability when wind speed is above 2 m·s-1 | |
图 8(b)是位温梯度与风向切变的联系,图 8(d)是BRi与风向切变的联系。风向切变与位温梯度的相关系数为0.54,拟合关系为Y=1.55X+0.05。随着位温梯度的增加,风向切变有增加的趋势。当位温梯度大于0时,风向随高度增加有顺时针旋转;当位温梯度接近0时,上下层风向趋于一致,风向切变趋于0;当位温梯度小于0时,风向随高度增加有逆时针旋转。风向切变与位温梯度、BRi的分布接近。从上文图 5中风速风向的时间序列,可以直观地发现风速风向在垂直上的差异存在一定的日变化分布。
4.2 不同大气稳定下的风场垂直分布上述测风塔的分析结果表明,大气温度层结的状态可以显著影响风的垂直分布,统计不同大气稳定度下各个高度上的温度、风速、风向,可以给出更为直观的结果。图 9是不同大气稳定度状况下大气的垂直分布:图 9(a)~9(e)分别是温度廓线、平均风速廓线、东西方向的风速分量、南北方向的风速分量、风向廓线。上三角形对应不稳定温度层结,蓝色下三角形对应稳定温度层结,黑色圆点对应中性温度层结。图 9中上三角形表示热量通量向上传输。统计时,样本选择140 m高度风速在5~8 m·s-1范围内的时刻。
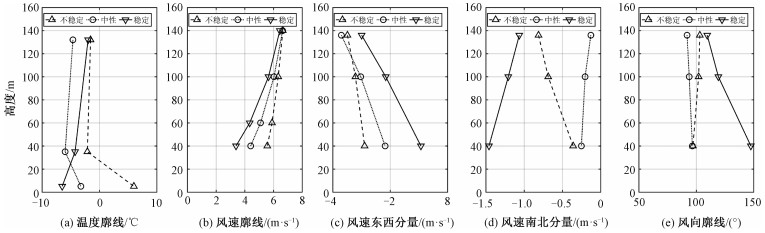
|
Download:
|
| 图 9 不同稳定度状况下大气温度和风场的垂直分布 Fig. 9 Vertical distribution of the atmosphere under different atmospheric stability conditions | |
夏季白天是图 9中上三角及虚线对应的典型情况:1)温度层结不稳定,地面温度显著高于高空;2)湍流运动使上下空气混合,向上输送热通量;3)湍流运动同时会向下输送更多的动量通量,低层大气速度更接近于高层。因此,不稳定层结时,风切变通常较小。
图 9(c)和9(d)是大气风廓线在东西方向、南北方向上的分量,图 9(c)中上三角对应的低层大气在东西方向有更大的速度分量,表明大气的湍流运动使高层大气的西风更多地向下输送,图 9(e)中不稳定温度层结下的低层更偏向西风方向,风向更接近90°。
表 2对图 9数据的统计表,温度梯度采用132和1 m这2个高度计算,风速切变、风向切变分别通过式(6)和式(7)采用140和40 m这2个高度计算。通常测风塔高度和风机叶轮中心高度都在100 m附近,温度梯度和风向切变计算时高度单位采用hm,即100 m。在中性温度层结下,风速切变为0.051,风向切变为-4.6(°)·hm-1,温度梯度为-1.1 ℃·hm-1,与干绝热递减率-0.98基本一致。在稳定温度层结下,地面温度较低,温度梯度较大,风速切变和风向切变均较大;在不稳定温度层结下,风速切变和风向切变均较小。
|
|
表 2 不同大气温度层结下温度和风场的垂直分布 Table 2 Vertical distribution of temperature and wind under different atmospheric conditions |
为验证大气稳定对风切变的影响规律,本文选取其他场地的测风塔数据,场地位于德国北部(54.63°N,9.31°E),测风塔高100 m,数据时间为2021年3月1日到2021年5月31日。风速切变选用100和29 m高度风速数据计算,风向切变选用97和54 m高度上的风向数据计算,温度梯度选用95和53 m上的温度数据计算。数据统计时,同样选取风速大于5 m·s-1的样本数据。
大气不稳定度的增加会增加大气的风速切变,当位温垂直梯度到达0.08 K·hm-1后,大气不稳定度的增加并不能继续增加风速切变,风速切变保持在0.4左右。图 8和图 10中风速切变随大气稳定度的分布略有差异,主要影响因素考虑是测量的地点和时间的不同:图 8测量地点位于内陆,整体风切变较小,图 10距离海岸只有60 km,海岸附近的风切变总体要高于内陆平原地形;图 8测试时间为秋冬季,大气多为稳定状况,图 10的测量时间为春夏季节,大气不稳定状况较多。
|
Download:
|
| 图 10 稳定度对风速切变(a)和风向切变(b)的影响 Fig. 10 Impact of atmospheric stability on wind shear (a) and wind veer (b) | |
当位温梯度大于0时,风向随高度增加有顺时针旋转;当位温梯度接近0时,上下层风向趋于一致,风向切变趋于0;当位温梯度小于0时,风向随高度增加有逆时针旋转。验证项目的结论与测试场地的观测结果一致。
5 结论本文通过外场观测测试研究大气稳定度对于风速切变和风向切变的影响,结论如下:
1) 大气稳定度对风速、风向风切变的影响显著,风速切变与位温垂直梯度的相关系数为0.48,拟合关系为Y=2.01X+0.27;风向切变与位温垂直梯度的相关系数为0.54,拟合关系为Y=1.55X+0.05。
2) 风速切变随位温梯度的增加而增加,当位温梯度到达0.08 K·m-1后,风速切变保持在0.35~0.40。当位温梯度大于0时,风向随高度增加有顺时针旋转;当位温梯度接近0时,上下层风向趋于一致,风向切变趋于0;当位温梯度小于0时,风向随高度增加有逆时针旋转。
3) 定量分析表明,中性温度层结下,温度梯度为-1.1 K·hm-1,风速切变为0.051,风向切变为-4.6 (°)·hm-1,温度梯度与干绝热递减率-0.98 K·hm-1接近;温度梯度大于0时,地面温度较低,风速切变和风向切变均较大;温度梯度小于0时,风速切变和风向切变均较小。
| [1] |
Krogs ter O, Reuder J. Validation of boundary layer parameterization schemes in the weather research and forecasting (WRF) model under the aspect of offshore wind energy applications-part Ⅱ: Boundary layer height and atmospheric stability[J]. Wind Energy, 2015, 18(7): 1291-1302. Doi:10.1002/we.1765 |
| [2] |
Werapun W, Tirawanichakul Y, Waewsak J. Wind shear coefficients and their effect on energy production[J]. Energy Procedia, 2017, 138: 1061-1066. Doi:10.1016/j.egypro.2017.10.111 |
| [3] |
黄轩, 郑佳锋, 张杰, 等. 西宁机场一次低空风切变的结构和特征研究[J]. 激光技术, 2022, 46(2): 206-212. Doi:10.7510/jgjs.issn.1001-3806.2022.02.010 |
| [4] |
International Civil Aviation Organization. Manual on low-level wind shear[M]. Ottawa, Canada: International Civil Aviation Organization, 2005: 5-27.
|
| [5] |
Gultepe I, Sharman R, Williams P D, et al. A review of high impact weather for aviation meteorology[J]. Pure and Applied Geophysics, 2019, 176(5): 1869-1921. Doi:10.1007/s00024-019-02168-6 |
| [6] |
周艳宗, 王冲, 刘燕平, 等. 相干测风激光雷达研究进展和应用[J]. 激光与光电子学进展, 2019, 56(2): 020001. Doi:10.3788/LOP56.020001 |
| [7] |
夏俊荣, 王普才, 闵敏. 新型多普勒测风激光雷达Windcube的风参数观测与验证[J]. 气候与环境研究, 2011, 16(6): 733-741. |
| [8] |
马晓梅, 王博, 刘永前. 一种基于大气稳定度的风资源评估方法[J]. 可再生能源, 2020, 38(1): 47-52. Doi:10.13941/j.cnki.21-1469/tk.2020.01.009 |
| [9] |
Gualtieri G, Secci S. Methods to extrapolate wind resource to the turbine hub height based on power law: a 1-h wind speed vs. Weibull distribution extrapolation comparison[J]. Renewable Energy, 2012, 43: 183-200. Doi:10.1016/j.renene.2011.12.022 |
| [10] |
郝辰妍, 许昌, 薛飞飞, 等. 基于热稳定度风向标准差法的风速外推模型研究[J]. 可再生能源, 2018, 36(5): 737-742. Doi:10.13941/j.cnki.21-1469/tk.2018.05.018 |
| [11] |
毕雪岩, 刘烽, 吴兑. 几种大气稳定度分类标准计算方法的比较分析[J]. 热带气象学报, 2005, 21(4): 402-409. Doi:10.3969/j.issn.1004-4965.2005.04.008 |
| [12] |
李祥余. 大气稳定度分类方法及判据比较研究[J]. 环境与可持续发展, 2015, 40(6): 93-95. Doi:10.19758/j.cnki.issn1673-288x.2015.06.026 |
| [13] |
李琼, 叶燕翔, 李福娇, 等. 广东各地Pasquill稳定度频率的分布特征[J]. 热带气象学报, 1996, 12(2): 181-187. Doi:10.16032/j.issn.1004-4965.1996.02.011 |
| [14] |
袁万, 彭秀芳, 胡煜. 大气稳定度对内陆低风速风电场发电量影响研究[J]. 太阳能学报, 2018, 39(8): 2133-2138. |
| [15] |
Li J, Guo J P, Xu H, et al. Assessing the surface-layer stability over China using long-term wind-tower network observations[J]. Boundary-Layer Meteorology, 2021, 180(1): 155-171. Doi:10.1007/s10546-021-00620-6 |
| [16] |
王蓉, 范绍佳, 鲍若峪. 广东沿海地区大气稳定度的分类方法探讨[J]. 热带气象学报, 2011, 27(2): 251-256. Doi:10.3969/j.issn.1004-4965.2011.02.014 |
| [17] |
范绍佳, 鲍若峪, 罗小芬, 等. 广东沿海地区大气稳定度及其分类探讨[J]. 中山大学学报(自然科学版), 1997, 36(1): 79-83. |
| [18] |
范绍佳, 林文实, 苏雄晖, 等. 理查逊数Ri在沿海近地层大气稳定度分类中的应用[J]. 热带气象学报, 1999, 15(4): 370-373, 34. Doi:10.16032/j.issn.1004-4965.1999.04.011 |
| [19] |
Peng Z, Sun J N. Characteristics of the drag coefficient in the roughness sublayer over a complex urban surface[J]. Boundary-Layer Meteorology, 2014, 153(3): 569-580. Doi:10.1007/s10546-014-9949-8 |
| [20] |
彭珍, 胡非, 蒋维楣, 等. 地气通量中存贮和平流项计算方案的探讨[J]. 气候与环境研究, 2009, 14(2): 113-119. |
| [21] |
彭珍, 宋丽莉, 胡非, 等. 台风"珍珠"登陆期间动量通量的多尺度分析[J]. 热带气象学报, 2012, 28(1): 61-67. Doi:10.3969/j.issn.1004-4965.2012.01.007 |
| [22] |
盛裴轩, 毛节泰, 李建国. 大气物理学[M]. 2版. 北京: 北京大学出版社, 2013.
|
| [23] |
International Electrotechnical Commission (IEC). Wind energy generation systems-Part 12-1: Power performance measurements of electricity producing wind turbines: IEC 61400-12-1: 2017[S/OL]. (2017-03-03)[2021-02-23]. https://webstore.iec.ch/publication/26603.
|
| [24] |
Wharton S, Lundquist J K. Assessing atmospheric stability and its impacts on rotor-disk wind characteristics at an onshore wind farm[J]. Wind Energy, 2012, 15(4): 525-546. Doi:10.1002/we.483 |
| [25] |
Stull R B. An Introduction to boundary layer meteorology[M]. Dordrecht: Springer Netherlands, 1988. Doi:10.1007/978-94-009-3027-8
|
| [26] |
毕雪岩, 刘烽, 陈辉, 等. 北京地区大气稳定度垂直分布特征[J]. 热带气象学报, 2003, 19(S1): 173-179. Doi:10.16032/j.issn.1004-4965.2003.s1.020 |
| [27] |
Murphy P, Lundquist J K, Fleming P. How wind speed shear and directional veer affect the power production of a megawatt-scale operational wind turbine[J]. Wind Energy Science, 2020, 5(3): 1169-1190. Doi:10.5194/wes-5-1169-2020 |
 2024, Vol. 41
2024, Vol. 41 


