月球没有活跃的板块运动，其冷却产生的热应力得以长时间积累，因此热应力成为影响月球内部力学环境的重要因素之一。由于月球内部的冷却速度大于表面，故热应力的总体分布为径向拉张和切向挤压^[1]。研究者对美国宇航月球勘测卫星(lunar reconnaissance orbiter)在月球表面观测到的逆冲断层进行了分析，推测它们是月球冷却产生的切向挤压应力的产物^[2-3]。同时，由于阿波罗月震实验(Apollo lunar seismic experiments package)记录到的28次浅源月震中有8次落在被解释为逆冲断层的地形陡坎附近30 km以内^[4]，因此月球浅部的热应力释放可能是触发浅源月震的原因之一。

除浅源月震，发生在半径600~1 000 km区域内的深源月震也可能与月球冷却产生的热应力存在关联。由于深源月震数据与月球潮汐表现出相同的周期性(27 d的月地轨道周期和206 d的太阳扰动周期)^[5-6]，因此普遍认为深源月震与月球的潮汐应力相关^[7-8]。然而，张贝等^[9]的计算表明，若假设月球为分层弹性介质，则月幔深部的潮汐应力远未达到足以触发月震的数量级。为解释潮汐作用触发深源月震的机制，张贝等^[9]提出在深源月震多发区存在高压孔隙流体的假设，认为孔隙流体分担了大部分静岩压力，使得发生破裂所需的差应力减小。月球内部普遍存在的径向拉张热应力为月幔深部孔隙的发育提供了一种可能的解释，将在第4节做详细讨论。

尽管月球冷却产生的热应力可能是月震活动的影响因素之一，但由于对月球各圈层的力学性质缺乏足够了解，目前对月球热应力积累的定量计算很少。我们使用一维参量化模型^[10]计算了月球的冷却和热应力积累过程，计算结果表明月球冷却产生的热应力在浅部以切向挤压为主，足以产生逆冲断层并触发浅源月震，而深部的差应力较小，因此热应力不是触发深源月震的直接原因。受计算方法的限制，我们的一维参量化模型采用弹性本构关系计算热应力，而对大时间尺度下不可忽略的黏性效应只做了简化定量计算。本研究使用三维黏弹性有限元模型计算月球热应力的积累过程，通过对比实验分析黏性参数对热应力的影响，并进一步讨论热应力和月震之间的关系。

1 数值模型 1.1 控制方程

若将月球的冷却过程用一阶差分格式离散成有限个时间步，则每个时间步内的力学状态可以近似看作平衡状态。第n个时间步的平衡方程可表示为

$ -\nabla \cdot\left(\boldsymbol{\sigma}^{n-1}+\Delta \boldsymbol{\sigma}^n\right)=\rho \boldsymbol{g}, $

(1)

其中：σ^n-1和Δσⁿ分别表示第n-1时间步的应力和第n时间步的应力增量，ρ为密度，g为重力加速度。记σ=σ_thermo+σ_litho，其中：σ_thermo为热应力，σ_litho为静岩压力，满足▽·σ_litho=ρg。本实验中，因月球冷缩导致的密度和重力变化可忽略不计，静岩压力的变化Δσ_lithoⁿ近似为零。因此热应力满足的平衡方程为

$ \nabla \cdot\left(\boldsymbol{\sigma}_{\text {thermo }}^{n-1}+\Delta \boldsymbol{\sigma}_{\text {thermo }}^n\right)=0. $

(2)

本实验采用Maxwell黏弹性模型模拟月壳和月幔的力学性质^[11-12]，其本构方程为

$ \Delta \boldsymbol{\varepsilon}^n=\Delta \boldsymbol{\varepsilon}_{\text {elasto }}^n+\Delta \boldsymbol{\varepsilon}_{\text {visco }}^n+\Delta \boldsymbol{\varepsilon}_{\text {thermo }}^n, $

(3a)

$ \Delta \boldsymbol{\varepsilon}_{\text {elasto }}^n=\boldsymbol{C}^{-1}: \Delta \boldsymbol{\sigma}_{\text {thermo }}^n, $

(3b)

$ \Delta \boldsymbol{\varepsilon}_{\text {visco }}^n=\boldsymbol{Q}^{-1}: \boldsymbol{\sigma}_{\text {thermo }}^n \Delta t^n $

(3c)

$ \Delta \boldsymbol{\varepsilon}_{\text {thermo }}^n=\alpha \Delta T^n \boldsymbol{I}, $

(3d)

其中：Δεⁿ为应变增量，Δtⁿ为第n个时间步的大小，α为线膨胀系数，ΔTⁿ为温度增量，I为单位矩阵。C和Q分别表示弹性应力-应变张量和黏性应力-应变率张量。对于三维各向同性介质，有

$ C_{i j k l}=\mu\left(\delta_{i k} \delta_{j l}+\delta_{i l} \delta_{j k}\right)+\lambda \delta_{i j} \delta_{k l}, $

(4a)

$ Q_{i j k l}^{-1}=\frac{1}{4 \eta}\left(\delta_{i k} \delta_{j l}+\delta_{i l} \delta_{j k}\right)-\frac{1}{6 \eta} \delta_{i j} \delta_{k l}, $

(4b)

其中：λ和μ为Lamé常数，η为黏性系数。

由式(3a)~(3d)可以得到热应力增量Δσ_thermoⁿ的表达式(注意到σ_thermoⁿ=σ_thermo^n-1+Δσ_thermoⁿ):

$ \Delta \boldsymbol{\sigma}_{\text {thermo }}^n=\tilde{\boldsymbol{C}}:\left[\Delta \boldsymbol{\varepsilon}^n-\boldsymbol{Q}^{-1}: \boldsymbol{\sigma}_{\text {thermo }}^{n-1} \Delta t^n-\alpha \Delta T^n \boldsymbol{I}\right], $

(5)

其中$ \tilde{\boldsymbol{C}}=\left(\boldsymbol{C}^{-1}+\boldsymbol{Q}^{-1} \Delta t^n\right)^{-1}$为黏弹性应力-应变张量。将式(5)代入式(2)，即可得到准静态Maxwell黏弹性模型的控制方程

$ \begin{gathered} -\nabla \cdot\left(\tilde{\boldsymbol{C}}: \Delta \boldsymbol{\varepsilon}^n\right)= \\ \nabla \cdot\left(\boldsymbol{\sigma}_{\text {thermo }}^{n-1}-\tilde{\boldsymbol{C}}: \boldsymbol{Q}^{-1}: \boldsymbol{\sigma}_{\text {thermo }}^{n-1} \Delta t^n-\alpha \Delta T^n \tilde{\boldsymbol{C}}{: \boldsymbol{I})}\right.. \end{gathered} $

(6)

式(6)中，温度增量ΔTⁿ是半径r和时间t的函数。使用一维参量化模型得到的月球温度变化数据，将ΔTⁿ作为已知量代入式(6)，使用有限单元法计算得到应变增量Δεⁿ，进而通过式(5)得到各个时间步的热应力增量Δσ_thermoⁿ和热应力值σ_thermoⁿ。

1.2 几何模型和初边值条件

将月球简化为分层的对称球体，建立1/8球壳模型。模型外边界代表月球表面，半径1 740 km，设为自由边界；内边界为核幔边界，半径400 km，由于月球外核为不可压缩流体，其体积变化只和温度相关，因此核幔边界设为Dirichlet边界，外核半径r_c的变化率$ \dot{r}_{\mathrm{c}} / r_{\mathrm{c}}=\alpha \dot{T}_{r=r_{\mathrm{c}}}$。模型和笛卡尔坐标轴平行的3个边界均为自由滑动边界。在有限元函数库deal.Ⅱ (version 9.3)^[13]的基础上编写有限元并行计算程序，使用六面体一阶Lagrange单元进行空间离散，径向共分64层，总单元数和总自由度数分别为12 288和42 315。为兼顾计算精度和计算效率，对网格的径向疏密进行了调整，月表附近和月幔底部径向分辨率为10 km，月幔中部径向分辨率为64 km。

通过一维参量化模型计算得到自月球形成至今约4.5 Ga的温度变化数据。但月球早期的月幔对流活动较为活跃，可能发生过影响整个月壳和月幔的“月幔翻转”现象^[14-18]，此时使用球对称模型不能反映月球内部的真实力学状态。因此，将模拟时间限定在月幔活动较弱的500 Ma至今，假定初始状态为应力平衡状态(σ_thermo⁰=0)，计算月球在500 Ma的近匀速冷却过程中热应力的积累和松弛，时间步长取为0.1 Ma。

1.3 物性参数

本实验中影响计算结果的物性参数包括线膨胀系数α、Lamé常数λ和μ，以及黏性系数η。其中，线膨胀系数α在整个模型中取为常数10^-5 K^-1[14]，而弹性参数和黏性系数则随半径变化。弹性参数可以通过下式与月球的密度和波速结构直接关联：

$ V_{\mathrm{p}}=\sqrt{\frac{\lambda+2 \mu}{\rho}}, V_{\mathrm{s}}=\sqrt{\frac{\mu}{\rho}}, $

(7)

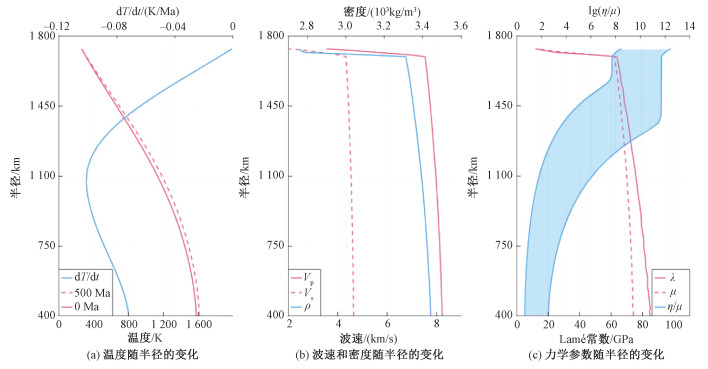
其中：V_p和V_s分别为纵波波速和横波波速。目前，研究者在阿波罗计划提供的月震数据基础上使用不同方法计算得到了多种波速结构^[19-21]，这些波速结构在细节上虽然不尽相同，但反映出的月震波波速随半径变化的趋势是相似的。我们选用Garcia等^[20]提出的密度和波速结构(图 1(b))，计算得到的弹性参数随半径的变化曲线如图 1(c)所示。

相对于弹性参数，人们对于月球内部介质黏性系数的认知更加模糊。在前人的月球动力学演化模型中，普遍假设月幔的物质组分与地幔相似，满足Arrhenius定律^{[14, 16-18]}

$ \eta_{\text {eff }}=\eta_0 \exp \left(\frac{E_{\text {eff }}}{R T}-\frac{E_{\text {eff }}}{R T_{\text {ref }}}\right), $

(8)

其中：R为理想气体常数，E_eff为有效活化能，T_ref为参考温度，η₀为T_ref下的参考黏度。式(8)对一般情形下的Arrhenius定律做了简化，省略了环境应力和岩石粒径对黏度的影响。Zhang等^[16]指出，若在式(8)中取E_eff=100~400 kJ/mol，则计算得到的有效黏度与使用标准Arrhenius定律和实验室条件下测得的橄榄石活化能(335~670 kJ/mol)^[22]计算得到的有效黏度相当。对于参考黏度η₀，实验和观测给出的约束较少，数值实验中通常取η₀=10¹⁹~5×10²¹ Pa·s^[16-18]。本实验中，对E_eff=100, 200, 300 kJ/mol和η₀=10¹⁹, 10²⁰, 10²¹ Pa·s的情况分别进行计算，以观察黏性参数对热应力的影响。不同流变参数计算得到的黏性系数随半径r变化的曲线如图 1(c)所示。

由于月球内部温度的跨度很大，按式(8)计算会得到不符合实际的黏度值，因此在实际计算中通常将黏度限制在一定范围内。使用公式

$ \eta=\frac{1}{\frac{1}{\eta_{\text {eff }}}+\frac{1}{\eta_{\max }}} $

(9)

计算实际黏度, 其中黏度上限η_max在模型中代表月球浅部的黏性系数，直接影响月壳的应力松弛时间。在多数以月幔对流为主的动力学演化模型中，出于数值稳定的需要，通常将η_max限定在10²⁵ Pa·s左右。在Kamata等^[11]和Qin等^[12]的黏弹性月球模型中，η_max分别取为10²⁸和10³⁰ Pa·s，从而保证月球浅部表现出以弹性为主的力学性质。本实验中，对η_max=10²⁶, 10²⁸, 10³⁰ Pa·s的情况分别进行计算，以观察月球浅部黏性系数对应力松弛的影响。

为方便叙述，下文中使用ExxxMxxCxx的方式描述模型中各个参数的取值，其中E指代有效活化能E_eff，M指代月幔参考黏度η₀，C指代黏性系数最大值η_max(即岩石圈黏度)。例如，模型E100M21C30中各个参数取值为E_eff=100 kJ/mol，η₀=10²¹ Pa·s，η_max=10³⁰ Pa·s。同时，省略热应力的下标thermo，若无特殊说明，下文中的σ均指热应力。

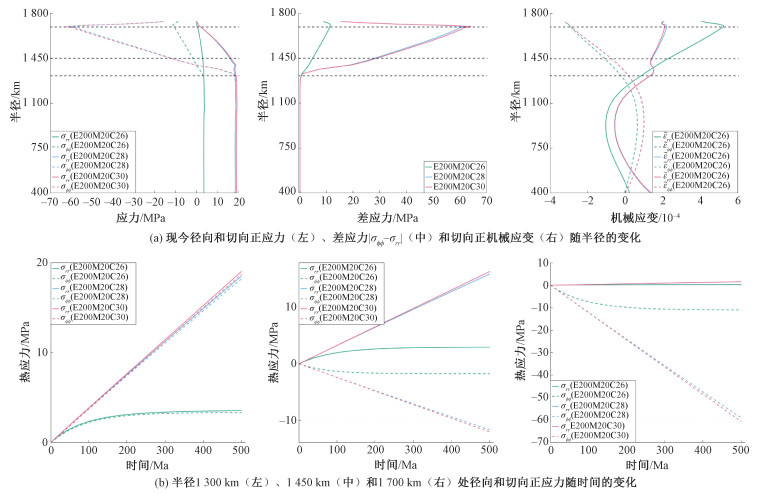
2 计算结果 2.1 月球岩石圈黏度对热应力松弛的影响

图 2展示了模型E200M20C26、E200M20C28和E200M20C30的计算结果。由图 2(a)可知，热应力随半径的变化大致分成3段：400 km＜r＜1 300 km时，σ_rr和σ_ϕϕ基本相等且不随r变化，热应力为拉张状态；1 300 km＜r＜1 700 km时，σ_rr逐渐减小，而σ_ϕϕ迅速变化至强烈挤压状态，于r=1 700 km处差应力达到最大值；r>1 700 km时，σ_rr和σ_ϕϕ的绝对值均逐渐减小，在月表处σ_rr变为0。

图 2的计算结果可以通过简化的一维模型来解释：对于一维Maxwell体，当温度随时间线性变化时，热应力一面积累、一面松弛，按下式的形式变化

$ \sigma=\sigma_{\max }\left[1-\exp \left(-\frac{t}{t_0}\right)\right], $

(10)

其中：t₀=η/E为松弛时间，σ_max为最终达到平衡时的应力值。式(10)的图像为：起始时刻应力近似呈线性增长，然后渐渐变缓，最后趋于一个稳定值，即温度匀速变化时，应力的积累和松弛达到动态平衡。温度线性变化的速率越大、松弛时间越长，则σ_max的绝对值越大，反之σ_max的绝对值越小。在我们的数值模型中，月球浅部的黏性系数很高(η≈η_max)，松弛时间很长。当η_max≥10²⁸ Pa·s时热应力在500 Ma内几乎一直处在近似线性增加的阶段，表现接近弹性体；而月幔深部黏性系数低，松弛时间短，很快达到热应力积累和松弛接近动态平衡的阶段。

由式(5)可知，温度变化率dT/dt和力学参数E, ν, η在空间上的变化都会影响热应力的分布。为更准确地分析模型内部的热应力状态，图 2(a)右展示了机械应变$ \tilde{\boldsymbol{\varepsilon}}$随半径的变化，其中$ \tilde{\boldsymbol{\varepsilon}}$的定义为

$ \tilde{\boldsymbol{\varepsilon}}=\varepsilon-\boldsymbol{\varepsilon}_{\text {thermo }}=\varepsilon-\alpha\left(\left.T\right|_{t=0}-\left.T\right|_{t=500 \mathrm{Ma}}\right) \boldsymbol{I} . $

(11)

对比图 2(a)左和2(a)右，可以看出径向正机械应变$\tilde{\varepsilon}_{r r} $直接反映了温度变化速率dT/dt的空间变化。其中，模型E200M20C26在所有深度热应力的加载和松弛都已达到动态平衡，因此$\tilde{\varepsilon}_{r r} $与dT/dt随半径的变化曲线表现出相同的趋势，只在月壳范围(0~40 km)因弹性参数的变化而有所差异。相对地，模型E200M20C28和E200M20C30在浅部并未松弛，因此$\tilde{\varepsilon}_{r r} $的变化曲线只在r＜1 300 km时与dT/dt相吻合，而当r>1 300 km时弹性性质占主导地位，因而变形小于E200M20C26模型。另一方面，切向正机械应变$\tilde{\varepsilon}_{\phi \phi} $因体积不均匀收缩而总体上呈现挤压状态，在热应力加载和松弛平衡的区域近似有$\tilde{\varepsilon}_{\phi \phi} $≈-0.5$\tilde{\varepsilon}_{r r} $(体积不受机械压缩)。

根据$\tilde{\varepsilon}_{r r} $随半径变化的曲线，将模型E200M20C28和E200M20C30的热应力状态分成3段：400 km＜r＜1 300 km时处于加载和松弛动态平衡的状态；1 300 km＜r＜1 450 km时处于加载大于松弛的状态；r>1 450 km时处于未松弛状态。在模型应力状态转变的节点(r=1 300 km和r=1 450 km)以及切向正应力的极值点(r=1 700 km，月壳底部)分别绘制了径向和切向正应力随时间变化的曲线(图 2(b))。可以看到，3个模型在r≤1 300 km时虽然均达到热应力加载和松弛平衡的状态，但径向和切向正应力仍随时间变化，且变化趋势与浅部径向正应力的变化趋势相同。这是因为模型深部的力学性质完全由黏性主导，在球对称的情况下热应力接近“静水压”状态。相对地，由于模型浅部(r>1 450 km)的力学性质由弹性主导，而月壳和月幔的剪切模量相差近1个数量级(见图 1(c))，因此切向挤压应力在月壳底部达到极值，在月壳内部随半径增大而减小。

图 2(b)表明，模型E200M20C26的浅部热应力在500 Ma时基本达到加载和松弛平衡的状态，而模型E200M20C28和E200M20C30的热应力仍在匀速加载。实际上，按月幔的剪切模量为70 GPa估算，模型E200M20C26、E200M20C28和E200M20C30的最大松弛时间分别为5 Ma、0.5 Ga和50 Ga，因此后两者在模型时间尺度内的松弛量可忽略或近于可忽略。Kamata等^[11]指出，η_max≥10²⁸ Pa·s的岩石圈对应于干燥斜长石构成的月壳和干燥橄榄石构成的上月幔，而月球的自由空气重力异常数据支持月球岩石圈具有高黏度。因此，在后面的实验中统一取η_max=10³⁰ Pa·s。需要注意的是，我们在模型中假定月壳和岩石圈月幔具有相同的黏度，而实际上二者的黏度应当不同。但由于模型浅部的热应力状态完全由弹性主导，因此黏度数值1~2个数量级的差别并不影响计算结果。

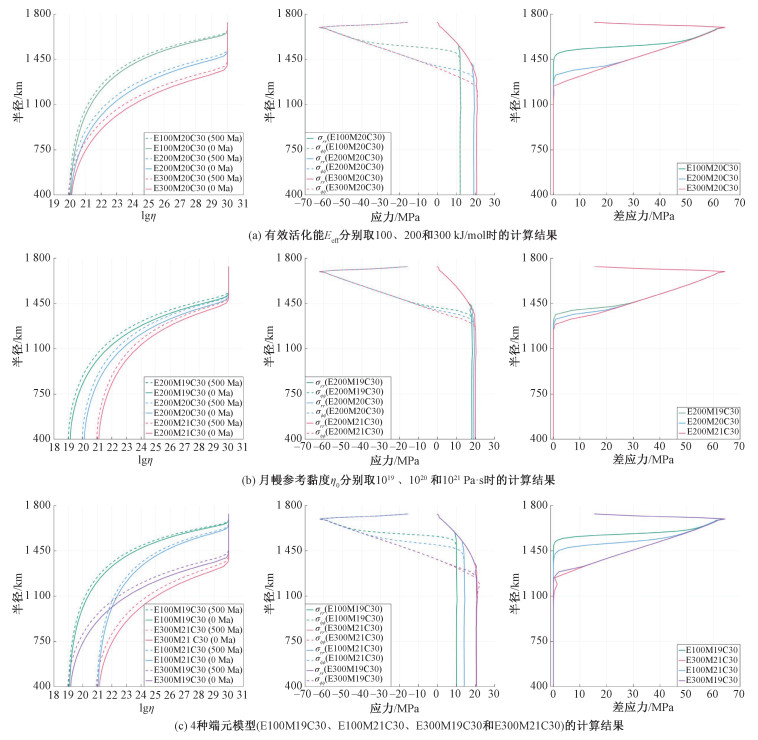
2.2 活化能和参考黏度对热应力分布的影响

有效活化能E_eff对热应力分布的影响如图 3(a)所示。随着E_eff增大，月幔黏度随半径增大的速度加快，导致热应力持续加载的区域更厚，模型E100M20C30、E200M20C30和E300M20C30中热应力加载和松弛达到平衡状态的深度分别为300、450和550 km。同时，更厚的弹性层使内部加载和松弛平衡区域所承受的“静水压”更大，模型E100M20C30和E300M20C30的下月幔热应力相差近2倍。月幔参考黏度η₀对热应力分布的影响如图 3(b)所示。由于η_max远大于η₀，弹性层厚度几乎不受η₀的影响，因此η₀对热应力的分布影响较小。

最后，给出4种端元模型(E100M19C30、E300M21C30、E100M21C30和E300M19C30)的计算结果(图 3(c))。在合理参数范围内(100 kJ/mol≤E_eff≤300 kJ/mol，10¹⁹ Pa·s≤η₀≤10²¹ Pa·s)，热应力加载和松弛达到平衡状态的最小和最大深度分别为250和550 km，下月幔所承受的拉张热应力的最小和最大值分别为10和20 MPa。所有模型均未在下月幔产生超过10 kPa的差应力。

2.3 现今月球内部热应力的估计

上述计算结果的一个显著特征是月幔中下部热应力的加载和松弛相平衡，接近于“静水压”状态，热应力的大小主要受浅部弹性层的径向热应力大小控制，而不受中下部月幔的局部扰动(例如月幔对流)的影响。因此，可以将数值模拟的起始时间前推。

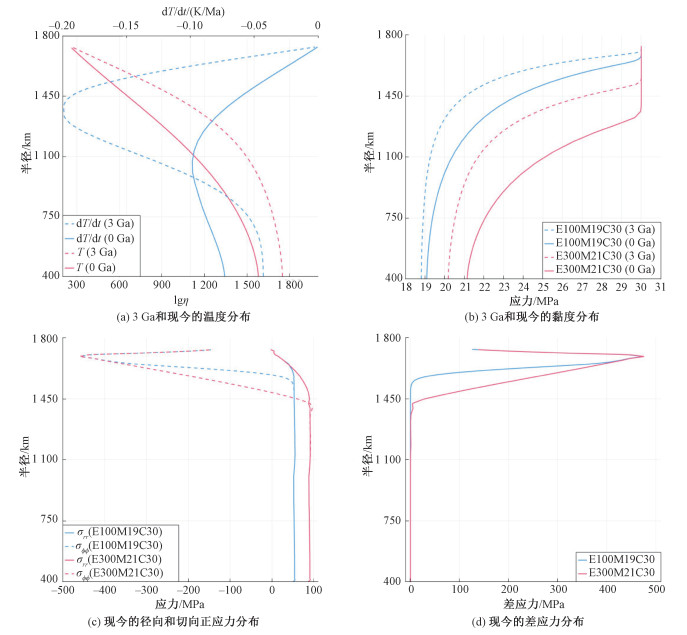
假设月幔发生过重力翻转事件，并将其视为对热应力的一次重置。文献[14, 16-18]的计算结果表明月幔翻转事件的持续时间为0.5~1.5 Ga左右，因此可以假定3 Ga之后不再发生波及整个月幔的对流事件，亦即3 Ga为热应力积累的起点。使用端元模型E100M19C30和E300M21C30模拟月球3 Ga至今的热应力演化，计算结果如图 4所示。

由图 4(a)可见，3 Ga时月球内部的温度分布和温度变化速率与现今差异明显。受温度的影响，3 Ga时月幔的黏性系数远低于现今(图 4(b))，因此在热应力演化的早期阶段中上月幔的黏性松弛时间很短，导致热应力加载和松弛达到平衡的深度比500 Ma至今的计算结果更浅(见图 4(c)和4(d)，模型E100M19C30和E300M21C30计算得到的热应力加载和松弛达到平衡的深度分别为200和300 km)。根据一维参量化模型的计算结果，月球岩石圈在3 Ga至今的时间范围内最薄时约300 km，因此月幔对流不会影响到浅部弹性层的热应力积累。在无应力释放的前提下，月表和月壳底部的切向挤压热应力分别积累达到150和460 MPa，月幔中下部的拉张热应力则达到60~90 MPa。值得注意的是，在上述计算中假设月球的弹性参数、有效活化能和参考黏度的分布在3 Ga的时间尺度上保持不变，而在实际的演化过程中月壳和月幔介质的力学性质可能发生更复杂的变化。因此，我们的计算结果可以看作对现今月球内部热应力分布的估计，进一步的研究依赖于更精细的数值模型和观测数据。

3 热应力与月震的联系 3.1 热应力与浅源月震的联系

如引言中所述，月球浅部的切向挤压热应力是引发浅源月震的可能因素之一。假设月壳介质遵循Coulomb-Mohr破裂准则，抗剪强度σ_s可表达为

$ \sigma_{\mathrm{s}}=C+\sigma_{\text {litho }} \sin \theta=C+\rho g h \sin \theta, $

(12)

其中：C为内聚力，θ为内摩擦角，h表示深度。应力Mohr圆与抗剪强度曲线相切时，有

$ \sigma_{\text {diff }} / 2=\rho g h \sin \theta+C \cos \theta, $

(13)

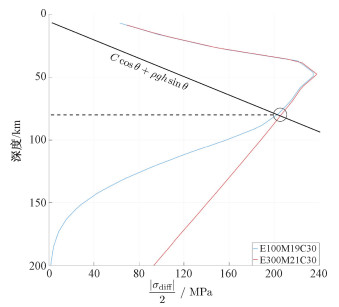
其中σ_diff/2=|σ_rr-σ_ϕϕ|/2为应力Mohr圆半径。为估计热应力可触发浅源地震的最大深度，近似取g=1.63 m·s^-2，ρ=3 300 kg·m^-3，C=1 MPa，θ=30°，此时σ_diff/2≥ρghsinθ+Ccosθ的范围为0~80 km (见图 5黑色虚线与纵轴的交点)，即月球浅部0~80 km深度范围内均有可能发生热应力导致的压性剪切破裂。目前对浅源月震的确切深度存在争议，通过不同波速模型得到的浅源月震最大深度在168~220 km不等^[23]。我们的估算结果给出的压性剪切破裂深度区间大致为浅源地震的震源深度区间的1/3。值得注意的是，内摩擦角θ的取值对压性剪切破裂的深度区间影响很大，±5°的差别会引起最大破裂深度∓10 km左右的变化。

3.2 热应力与深源月震的联系

相对于浅源月震，深源月震的发震原因更加难以解释。尽管深源月震与潮汐作用的关联得到普遍承认，但潮汐作用引起的差应力非常小(根据张贝等^[9]的计算，潮汐作用引起的最大剪应力不超过1 MPa)，远远达不到3~4 GPa围压下岩石的破裂极限。由于波速结构显示月幔底部可能存在熔融或部分熔融层^[24]，Frohlich和Nakamura^[25]认为处于熔融或部分熔融状态的月幔物质在潮汐应力的反复作用下发生疲劳，从而可以在较低的差应力下发生破裂。张贝等^[9]提出一种不同的思路，认为月幔深部可能存在孔隙结构(孔隙流体即为熔体)，岩石骨架承受的有效应力因孔隙压的存在而减小，从而大大降低了破裂强度。同时，月幔深部的孔隙流体可能在静岩压力作用下向上迁移，而在上月幔会受到切向挤压热应力的阻碍，从而形成类似于岩浆囊的构造。这一推论与深源月震大多丛集于一些特定区域形成“震源窝”的特征^[26]相吻合。

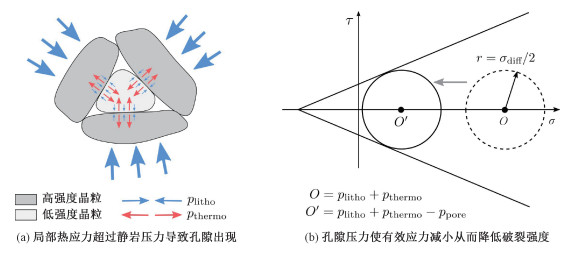
我们的计算结果为深部月幔孔隙结构的发育提供了一种解释，如图 6所示，图中p_litho表示静岩压力，p_thermo=-σ_rr=-σ_ϕϕ＜0表示月球冷却在月幔深部产生的拉张“静水压”，p_pore表示孔隙压，σ_diff表示潮汐作用引起的差应力。静岩压力的传递依靠矿物颗粒的相互挤压，在微观尺度上，不同的矿物颗粒由于组分、晶体结构、晶轴方向等等的不同导致力学强度存在差异，因而静岩压力的分布可能并不均匀。以图 6(a)所示的情况为例，3颗强度较高的晶粒形成一个结实的“骨架”承受了大部分的静岩压力，而位于其中的强度较低的晶粒所承受的静岩压力较小。与静岩压力不同，热应力不受矿物颗粒排布的影响，且多数矿物的热膨胀系数大小相近，因此可以认为热应力的分布比较均匀。由于深部月幔的拉张热应力可积累至数十~100 MPa，因此某些局部热应力的大小可能超过静岩压力，从而形成张裂隙。随着孔隙压力的增大，岩石的应力Mohr圆向左移(图 6(b))，因此潮汐作用形成的剪应力(~0.5 MPa)也有可能引起月幔深部的剪切破裂，从而触发深源月震。值得注意的是，静岩压力、热应力和孔隙压力共同作用下的有效应力可能为拉张状态，因此深源月震的震源机制可能并非走滑，而是张性破裂，这与深源月震的S波和P波振幅分析结果^[27]相符。这种解释隐含的推测是深源月震应力降应该比较小，与实际观测到的应力降(约为0.05 MPa^{[8, 23]})也是吻合的。

4 结论

本研究使用三维黏弹性有限元模型计算月球匀速冷却的热应力积累过程。实验结果表明月球浅部弹性层中的热应力以切向挤压为主，而月幔深部的热应力因黏性松弛而呈现接近“静水压”状态，径向和切向正应力的大小完全受浅部径向热应力的控制，因此可以不受局部月幔活动的影响而从月球演化的早期阶段积累至今。在高黏度岩石圈假设下，现今月壳底部的切向挤压应力可积累达到400 MPa，相应的月幔深部拉张应力可达60~120 MPa。我们的计算结果为深源月震震源机制的孔隙流体假设提供了支持，而究竟潮汐应力、热应力和孔隙流体的共同作用能否使得深部月幔介质达到破裂条件，仍有待于进一步的研究。