由于正在使用的海上信息服务——船舶自动识别系统(automatic identification system, AIS)和特殊应用报文(application-specific messages, ASM)的信道容量已经趋于饱和，国际海事组织(International Maritime Organization，IMO)、国际航道标志协会(International Association of Lighthouse Authorities，IALA)和国际电信联盟(International Telecommunication Union，ITU)，共同提出建设未来海上通信平台VDES(VHF data exchange system)。为了争夺未来全球海上通信系统标准的制高点，依照VDES技术建议书^[1]和VDES技术规范草案^[2]，各个海洋强国积极投入到VDES系统的研究和建设中^[3-5]。超过10个国家正在计划或建造多颗VDES卫星，而出于国家安全需要，难以实现国家间的星间链路。因此，VDES异构星座兼容共存是未来发展的必然趋势。现有协议草案中所有VDES星座采用相同的频率、时间对齐方式和时隙表^[2]，导致重复覆盖区的链路大量冲突，严重影响系统整体性能，因此VDES多星座兼容是VDES建设关键问题之一。

现有机制通过扩频的调制编码方式和2个卫星专用信道使得重复覆盖区最多能同时收到4个不同星座的扩频信号^[2]。然而扩频信号的数据量是非扩频信号的1/131~1/2.5^[2]，无法充分满足应用数据的交互需求。

星座间兼容有硬兼容和软兼容2种方式，硬兼容指通过只改变硬件参数以达到兼容。星座间兼容已在全球导航卫星系统(Global Navigation Satellite System，GNSS)中提出，解决方法主要有功率控制、卫星姿态控制和天线覆盖范围控制等。VDES卫星具有单波束覆盖范围广、重复覆盖区面积大、重复覆盖率高的特点，导致功率控制、姿态控制的运算和控制开销大，无法使用。为了兼容地面通信，VDES卫星天线采用60°斜装，也无法控制覆盖范围。

软兼容指通过只改变软件协议，以达到兼容。随着卫星产业的商业化和规模化，地球静止轨道(geostationary earth orbits，GEO)卫星和低轨(low earth orbit，LEO)卫星逐渐成为星座间兼容的焦点。LEO卫星之间信息交互协作，在保证GEO卫星通信质量的同时，提高时间利用率和吞吐量^[6-8]。为进一步提升性能，在GEO卫星性能不明显下降的情况下，通过LEO和GEO星座联合资源控制，提高频谱效率^[9-10]。然而GEO和LEO共存时，GEO性能更加优先，受干扰更少，而VDES星座的优先程度相同。

近年来，由于深度强化学习(deep reinforcement learning，DRL)在序列决策问题上的优异性能^[11]，被广泛应用到通信资源分配上。针对LEO卫星的波束间资源分配问题，通过将通信请求的特征作为状态的一部分^[12]，降低了链路切换时的延迟，在此基础上增加对波束内资源的统筹^[13]，进一步提高整体性能。但这些策略仅针对单一系统的场景，目前缺乏针对多星座共存时通信链路特点的时隙分配研究。

基于以上分析，结合VDES通信的高时变性的特点，提出一种基于改进DQN算法的VDES多星座兼容策略。首先, 在现有VDES通信机制的基础上，设置船站作为时隙资源感知节点，使卫星能够获得所有其他卫星的历史资源分配信息；然后，将VDES通信资源分配过程建模成强化学习问题，以最大化长期动作收益总和为目标；最后通过状态重构及DQN算法对强化学习问题进行求解, 得到近似最优的资源分配策略，提高VDES通信的性能。

1 时隙分配DQN模型 1.1 异构VDES星座兼容策略

VDE-SAT是TDMA系统，一帧时长1 min，以一分钟的开始为一帧的开始。1帧有3个子帧，每个子帧包含发送、处理、传输的完整通信流程，有6个DC(data channel)时隙用于传输应用数据。卫星获取请求后，开始规划请求的分配，由于下行的DC时隙一定排在上行的DC时隙前面，导致所有卫星给同方向的请求分配的DC时隙具有趋同性^[2]。然后卫星广播分配方案，DC时隙被相应的终端占用传输应用数据。同序号的DC时隙被同一个终端占用直至应用数据全部传输完毕。

在自组织网络中，通过侦听信道能够感知其他终端的传输情况，降低碰撞^[14]，而VDES异构星座之间无法感知互相的时隙占用情况。在此启发下，针对星船通信特性，提出一种自组织星座间信息交互策略：卫星指定在重复覆盖范围内的某个船站作为时隙资源感知节点，然后向卫星转发其他星座卫星上个子帧的时隙分配信息。在不改变现有通信体制的情况下，达到星座间交互资源分配信息的目的。虽然卫星只能获得其他卫星上个子帧的分配情况，但历史DC时隙分配情况能为当前子帧的分配提供指引。上个子帧传输成功的DC时隙意味着该种分配方式具有较高的成功率，应为待发送请求选择最相似的分配方式。

根据其他消息的设计，设置资源分配信息消息为上行信令，指定船站作为节点的消息为下行信令。资源分配信息消息需要增加一次突发作为开销。上行信令采用扩频因子为8的扩频信号^[2]，因此增加资源分配信息不会对正常的上行信令传输造成过大影响。另一方面，指定船站作为节点的消息开销仅为6个字节，而卫星一个子帧最多传输234个字节的下行行令^[2]，即使有多个星座重复覆盖，该消息对下行信令的影响也有限。

1.2 系统模型

VDES时隙分配是一种序列决策问题，而当前子帧的分配会对未来产生影响，应着眼于长远利益，最大化未来的总传输成功时隙数量。

性能评估函数设为平均传输成功时隙数量P_S和时隙利用率P_U，P_S用于衡量策略的整体性能，P_U用于衡量策略对空闲时隙的利用程度。由于一个子帧是一个完整通信流程，P_S和P_U都基于子帧衡量，P_S定义为

$ P_{\mathrm{S}}=\sum\limits_{t=1}^T n_{\mathrm{suc}}^t /(6 \times T) $

(1)

其中：T为总子帧数，n_suc^t为第t个子帧中传输成功的DC时隙数量。P_U定义为

$ P_{\mathrm{U}}=\sum\limits_{t=1}^T n_{\mathrm{usd}}^t / \sum\limits_{t=1}^T n_{\mathrm{vac}}^t \text {, } $

(2)

其中: $n_{\text {vac }}^t$为第$t$个子帧中空闲DC时隙数量, $n_{\text {usd }}^t$为$n_{\text {vac }}^t$中被分配了请求且传输成功的DC时隙数量。

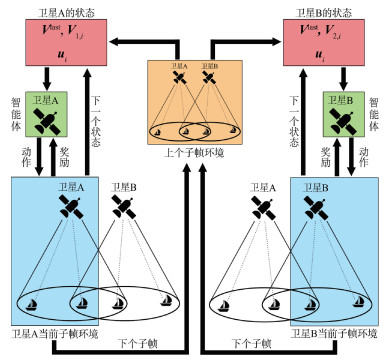
由于VDES系统时变性高，尚处于预研阶段，具有较少的先验信息，无法针对通信过程建立有效的系统模型。这使得传统的动态规划算法^[15-16]无法解决此类资源分配问题。因此，考虑通过基于无模型的强化学习算法^[17]获得最大化P_S的策略。由于P_S为离散值，无法直接作为目标函数进行优化，需要通过优化一种与P_S具有较强相关性的目标函数间接优化P_S。假如传输成功的DC时隙价值高，传输碰撞的DC时隙价值低，则P_S与所有DC时隙的总价值呈正相关。由于不分配时隙的操作也能通过降低碰撞率来提升DC时隙的价值，所以DC时隙的价值转换成操作的价值，将未来动作的总价值作为目标函数。基于以上分析，将时隙分配问题建模为RL问题，模型如图 1所示。

1) 状态: 状态是环境高度精简概括。假设在某个子帧, 第$k$个卫星收到的请求有$N$个。请求队列$\boldsymbol{u}=\left\{\boldsymbol{u}_1, \boldsymbol{u}_2, \cdots, \boldsymbol{u}_i, \cdots, \boldsymbol{u}_N\right\}$, 其中第$i$个请求$\boldsymbol{u}_i=\left\{u_i^1, u_i^2\right\}, u_i^1$表示该请求的通信方向, $u_i^2$为船站终端位置, 因为碰撞由同一DC时隙2个链路的通信方向和船站终端位置决定。

时弥状态矩阵(slot state matrix, SSM) 定义为$\boldsymbol{V}=\left\{\boldsymbol{V}_1, \boldsymbol{V}_2\right\}$, 其中$\boldsymbol{V}_1$和$\boldsymbol{V}_2$分别表示卫星A和卫星B的时隙状态, $\boldsymbol{V}_1$和$\boldsymbol{V}_2 \in \mathbb{R}^{6 \times 4}$, 其定义为

$ \boldsymbol{V}_k=\left[\begin{array}{cccc} v_1^1 & v_1^2 & \cdots & v_1^4 \\ v_2^1 & v_2^2 & \cdots & v_2^4 \\ \vdots & & & \vdots \\ v_m^1 & v_m^2 & \cdots & v_m^4 \\ \vdots & & & \vdots \\ v_6^1 & v_6^2 & \cdots & v_6^4 \end{array}\right] \text {, } $

(3)

其中: $k \in\{1, 2\}, m \in\{1, 2, \cdots, 6\}, v_m^1$代表是否被占用, $v_m^2$表示传输方向, $v_m^3$表示船站位置, $v_m^4$表示传输是否发生冲突。

针对VDE-SAT的高时变性和星座间的信息交互, 状态应该包含请求信息$\boldsymbol{u}_i$、处理$\boldsymbol{u}_i$时第$k$个卫星的时隙状态$\boldsymbol{V}_{k, i}$和处理完上个子帧的请求后所有卫星的时隙状态$\boldsymbol{V}^{\text {last }}$, 状态$\boldsymbol{s}_{k, i}$定义为

$ \boldsymbol{s}_{k, i}=\left\{\boldsymbol{V}^{\text {last }}, \boldsymbol{V}_{k, i}, \boldsymbol{u}_i\right\} \text {. } $

(4)

基于VDE-SAT的通信流程, 对于同一子帧的请求, 上个子帧传输结果一致, 所以这些请求对应$\boldsymbol{s}_{k, i}$中的$\boldsymbol{V}^{\text {last }}$也一致。

2) 动作：动作是对正在处理的请求执行的操作。对于每个请求有7种操作选择，即不分配时隙和分配6个DC时隙中的某一个。强化学习经过运算后，获得每个动作的预期价值，将其中价值最高的动作的索引输出。用分配时隙的索引表示动作a_i，动作a_i定义如下

$ a_i= \begin{cases}0, & \text { 不分配 DC 时隙, } \\ i, & \text { 分配第 } i \text { 个 DC 时隙. }\end{cases} $

(5)

3) 奖励：奖励表示当前请求的各个动作对当前状态有利程度。不同动作对时隙分配的影响不同，奖励应分为不分配时隙时和分配DC时隙时两种情况进行判断。

当前子帧空闲DC时隙较少时, 即$\sum\limits_m v_m^1 \geqslant 4$, 传输成功的时隙数量可能较大。不分配时隙能够降低碰撞、减少对其他卫星的影响, 价值较高, 应给予正数奖励。而且空闲时隙越少, 再分配请求造成碰撞的可能性越大, 所以不分配的奖励越大。当前子帧无空闲DC时隙时, $\sum\limits_m v_m^1=6$, 只能执行不分配的动作, 不分配的价值极高, 应获得极大的奖励。当前子帧空闲DC时隙较多时, 即$\sum\limits_m v_m^1 \leqslant$ 3, 为了提高传输成功时隙数量, 应鼓励给请求分配时隙, 不分配的动作价值低, 应不予以奖励。当$a_i=0$时, 奖励$r_i$定义如下

$ r_i=\left\{\begin{array}{ll} 0, & a_i=0 \& \sum\limits_m v_m^1 \leqslant 3, \\ \alpha_1, & a_i=0 \& \sum\limits_m v_m^1=4, \\ \alpha_2, & a_i=0 \& \sum\limits_m v_m^1=5, \\ 1, & a_i=0 \& \sum\limits_m v_m^1=6, \end{array} 0<\alpha_1<\alpha_2<1 .\right. $

(6)

当$a_{i} \neq 0$时, 首先需要考虑时隙分配的结果。为提高传输成功时隙数量, 传输是否成功决定奖励的正负。初始奖励$r^{\rm o}$判断奖励的正负, 由是否传输发生碰撞决定, 定义如下

$ r^{\rm o}=\left\{\begin{array}{cl} \beta, & a_{i} \neq 0 \& \text { 传输无碰撞, } \\ -\beta, & a_{i} \neq 0 \& \text { 传输有碰撞, } \end{array} \quad \beta>0 .\right. $

(7)

为进一步提升传输成功时隙数量，基于星座间信息交互策略，当前子帧的链路与上个子帧的链路越相似，请求传输成功的可能性越高，这样分配的动作价值也越高。在传输成功的基础上，$\boldsymbol{V}^{\text {last }}$中$\boldsymbol{v}_{k, a_{i}}$的方向和船站位置与$\boldsymbol{u}_{i}$的一致性越强, 奖励应越大, 设置每增加一个一致的特征, 奖励翻倍, 奖励$r_{i}$定义如下

$ r_{i}=\left\{\begin{array}{l}r^{\rm o}, a_{i} \neq 0 \& v_{k, a_{i}}^{2} \odot u_{i}^{1}+v_{k, a_{i}}^{3} \odot u_{i}^{2}=0, \\ \delta r^{\rm o}, a_{i} \neq 0 \& v_{k, a_{i}}^{2} \odot u_{i}^{1}+v_{k, a_{i}}^{3} \odot u_{i}^{2}=1, \delta>0 . \\ \delta^{2} r^{\rm o}, a_{i} \neq 0 \& v_{k, a_{i}}^{2} \odot u_{i}^{1}+v_{k, a_{i}}^{3} \odot u_{i}^{2}=2, \end{array}\right. $

(8)

2 基于DQN的时隙分配算法 2.1 DQN构架

为有效计算当前子帧的时隙分配结果对未来环境的影响，需要最大化未来动作的总价值。根据贝尔曼方程，在策略π下动作a_i的价值定义为

$ \begin{align*} & q_{\pi}(\boldsymbol{s}, a)=E_{\pi}\left(r_{i}+\gamma r_{i+1}+\gamma^{2} r_{i+2}+\cdots \mid \boldsymbol{s}=\boldsymbol{s}_{k, i}\right. \\ & \left.a=a_{i}\right)=r_{i}+\gamma \sum\limits_{\boldsymbol{s}^{\prime} \in S} P_{\boldsymbol{s} \boldsymbol{s}^{\prime}} \sum\limits_{a^{\prime} \in A} \pi\left(a^{\prime} \mid \boldsymbol{s}^{\prime}\right) q_{\pi}\left(\boldsymbol{s}^{\prime}, a^{\prime}\right) \end{align*} $

(9)

其中: $S$是所有状态的集合, $A$是所有动作的集合; $\sum\limits_{\boldsymbol{s}^{\prime} \in S} P_{\boldsymbol{s} \boldsymbol{s}^{\prime}} \sum\limits_{a^{\prime} \in A} \pi\left(a^{\prime} \mid \boldsymbol{s}^{\prime}\right) q_{\pi}\left(\boldsymbol{s}^{\prime}, a^{\prime}\right)$是在策略$\pi$下未来获得的奖励, 用来衡量一次请求分配对未来的影响; $\gamma$是折扣因子, 用于调整未来奖励的重要性, $\gamma \in(0, 1) ; P_{\boldsymbol{s} \boldsymbol{s}^{\prime}}$是状态$\boldsymbol{s}$变为状态$\boldsymbol{s}^{\prime}$的概率; $\pi\left(a^{\prime} \mid \boldsymbol{s}^{\prime}\right)$是当状态为$\boldsymbol{s}^{\prime}$时选择动作$a^{\prime}$的概率。为使长期利益最大化, 应选择未来奖励最大的动作$a_{\mathrm{opt}}$, 动作$a_{\mathrm{opp}}$定义如下

$ a_{\text {opt }}=\operatorname{argmax}_{a_{i} \in A} q_{*}\left(\boldsymbol{s}_{i}, a_{i}\right), $

(10)

其中, 行为价值函数$q_{*}\left(\boldsymbol{s}_{i}, a_{i}\right)$是当前状态对应的所有动作中的价值最大的, 其计算公式如下

$ q_{*}\left(\boldsymbol{s}_{i}, a_{i}\right)=r_{i}+\gamma \sum\limits_{\boldsymbol{s}_{i+1} \in S} P_{\boldsymbol{s}_{i} \boldsymbol{s}_{i+1}} \max _{a_{i+1}} q_{*}\left(\boldsymbol{s}_{i+1}, a_{i+1}\right) $

(11)

通过计算式(11)可以针对当前处理的请求得到最优决策，但由于状态空间过大，而且状态中的历史资源信息导致连续的状态之间具有强相关性，使得传统的RL算法计算量巨大又低效。而DQN算法^[18]的记忆池加抽样不仅能应对状态空间过大，而且能破坏强相关性，使强化学习快速有效，可以有效解决此类问题。

整个问题已经简化成寻找行为价值函数$q_{*}\left(\boldsymbol{s}_{i}, a_{i}\right)$最优值。Q网络用于输出特定状态下动作的价值, 即$\left(\boldsymbol{s}_{i}, a_{i}\right) \rightarrow Q\left(s_{i}, a_{i} \mid \theta\right)$, 其中$\theta$是$Q$网络的参数。为使状态更加精准地反映通信所需信息, 根据特征对当前子帧时隙状态$\boldsymbol{V}_{k, i}$和上个子帧时弥状态$\boldsymbol{V}^{\text {last }}$以及当前处理的请求$\boldsymbol{u}_{i}$进行重构, 如图 2所示。首先将2种传输方向和2种船站位置编码成4位独热码。然后$\boldsymbol{u}_{i}$在独热码后方填0重构成$1 \times 8$的向量。$\boldsymbol{V}_{k, i}$结合每个DC时隙是否被分配, 选择4位0或者4位独热码, 并在4位数据后面填0, 6个当前子帧DC时隙对应的重构向量组成$6 \times 8$的矩阵。$\boldsymbol{V}^{\text {last }}$在重构前需要先根据传输分析获得上个子帧的传输结果, 确定$v_{m}^{4}$的值, 而发生碰撞的DC时隙当成空闲时隙处理。每一个DC时隙再根据卫星自身是否传输成功, 判断独热码是由上个子帧$\boldsymbol{V}^{\text {last }}$中卫星自身的$\mathrm{SSM} \boldsymbol{V}_{k}$产生还是由其他卫星的$\mathrm{SSM} \boldsymbol{V}_{k^{\prime}}$产生, 确定独热码的位置, 并在空余的地方填0。6个上个子帧DC时隙对应的重构向量组成$6 \times 8$的矩阵。为使每个请求处理时的$\boldsymbol{V}^{\text {last }}$差异化, 将$\varphi\left(\boldsymbol{u}_{i}\right)$作为一个元素加人$\varphi\left(\boldsymbol{V}^{\text {last }}\right)$中。重构后的状态定义如下

$ \varphi\left(\boldsymbol{s}_{k, i}\right)=\varphi\left(\boldsymbol{V}^{\text {last }}, \boldsymbol{V}_{k, i}\right) $

(12)

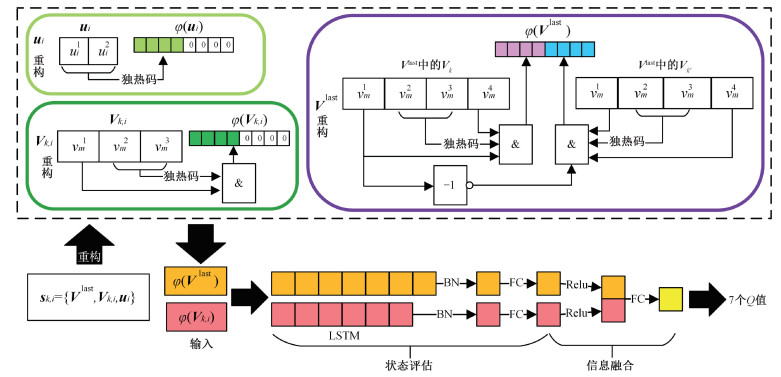
如图 2所示，Q网络的输入是具有2个元素的φ(s_i)，输出是7个动作的Q值。Q网络的结构分为状态评估和信息融合两部分。由于时隙分配具有有序、时间相关的特点，而且同时需要长期的通信环境特征和当前子帧的通信环境特征，所以使用2个长短期记忆(long-short term memory，LSTM) 层作为状态评估的网络，用以分析$\varphi\left(\boldsymbol{s}_{i}\right)$的每个元素。为融合分析结果，信息融合部分使用2个全连接(fully connected，FC)层。

2.2 DQN参数更新

为优化策略，需要通过迭代优化Q网络的参数θ。值得注意的是，与一般的强化学习问题不同，时隙分配问题没有终止状态。若当前子帧没有空闲时隙时，应拒绝以后的请求。该状态被认为是当前子帧的分配终止，设置为无效状态，其目标Q值的计算方式与其他状态不同。

损失函数$L(\theta)$表示当前状态下能够获得的最大未来奖励与$Q$网络输出动作对应未来奖励之间的差距, 即目标$Q$值$y_{i}$与实际$Q$值之差, 定义如下所示

$ L(\theta)=E\left[\left(y_{i}-Q\left(\varphi\left(\boldsymbol{s}_{i}\right), a_{i} ; \theta\right)\right)^{2}\right] $

(13)

目标Q值实际上只有在每次迭代结束后才能更新。在实际应用中，为降低运算量，引入时序差分(1-step TD)学习的概念，用当前奖励加上折扣后的未来奖励作为目标Q值, 因为受过部分训练的网络已经可以提供一个近似最优的策略。目标Q值y_i的计算公式为

$ y_{i}=\left\{\begin{array}{l} r_{i}+\eta, \quad \boldsymbol{s}_{i+1} \text { 为无效状态; } \\ r_{i}+\gamma \max _{a_{i+1}} \bar{Q}\left(\varphi\left(\boldsymbol{s}_{i+1}\right), a_{i+1} ; \bar{\theta}\right), \\ \boldsymbol{s}_{i+1} \text { 不为无效状态. } \end{array}\right. $

(14)

其中: $\bar{Q}$为具有参数$\bar{\theta}$的目标$Q$网络, $\eta$用于给无效状态赋值。

改进的DQN算法的主要实现过程如算法1所示, 分为初始化阶段和训练阶段。初始化阶段包括场景参数和模型参数的初始化。在更新Q网络参数的过程中, 使用$\varepsilon$-贪心算法用以提高动作空间探索程度。通过网络参数不断的更新迭代, 对决策评估越来越准确, 能得到近似最优的决策。

算法1基于改进DQN的时隙分配算法
初始化
初始化当前子帧的SSM、上个子帧的SSM、Q网络和经验池
训练
For请求$i=1: N$ do
只保留3个子帧之内达到的请求
由$\boldsymbol{V}_{k, i}$获得$\boldsymbol{s}_{i}$
if $\boldsymbol{s}_{i}$是无效状态 then
令ai=0
else
重构$\boldsymbol{s}_{i}$为φ($\boldsymbol{s}_{i}$)
使用ε-贪心算法获得动作ai
更新Vk, i
通过下一个请求获得$\boldsymbol{s}_{i+1}$，并重构为φ($\boldsymbol{s}_{i+1}$)
end if
标记$\boldsymbol{s}_{i+1}$是否是无效状态
if当前子帧的请求处理完毕 then
通过各个卫星的时隙分配，获得传输结果
根据传输结果获得动作ai对应的奖励ri
更新Vlast和Vk, i
将{φ(si), ai, ri, φ(si+1)}存入经验池
end if
从经验池中取一批元组计算L(θ)
根据L(θ)的值执行梯度下降
每G个子帧用θ=θ更新θ
End for

3 仿真结果

依照AIS和ASM的实际运行过程中的真实数据，VDES仿真参数设置如表 1所示。重复覆盖率为在重复覆盖区与卫星建立通信链路的船站在所有与卫星建立通信链路的船站中的占比，假设所有卫星的重复覆盖率相同。针对VDES海洋通信容量更大的特点，增加了业务传输所需时隙数量。业务的传输方向和船站位置服从平均分布。新请求到达率服从独立的泊松分布。策略参数如表 2所示。

由于分配实际由卫星执行，对分配产生影响的是请求的总数以及各类请求的比例，因此将平均一个子帧里卫星收到的新请求数量作为卫星请求到达数量，而重复覆盖率反映了船站位置的分布。为保证请求的实时性，每个请求最多被尝试分配3次，之后将作为旧请求被剔除。此外，将随机分配方法作为对照。随机分配方法为每个请求随机选择不分配时隙或者分配某个DC时隙。现有分配方法^[2]和随机分配方法均仅依靠卫星自身的分配信息，不具有通信环境感知能力。

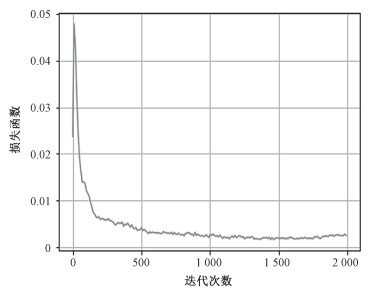
图 3显示了DQN算法的迭代收敛过程，在仿真过程中，卫星请求到达个数为12，重复覆盖率为0.5。从图 3中可以看出，DQN算法在经过200多次迭代后逐渐收敛，表明该算法能够通过历史资源分配信息和当前资源分配信息合理分配资源。

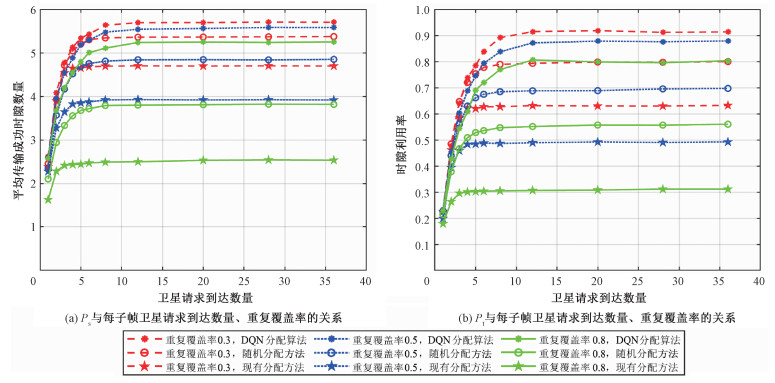
传输成功时隙数量P_S与卫星请求到达数量的仿真结果如图 4(a)所示。时隙利用率P_U与卫星请求到达数量的仿真结果如图 4(b)所示。由图 4可知，相比其他2种方法，基于DQN的分配算法在不同卫星请求到达数量、不同重复覆盖率的情况下都表现出更好的性能，证明了所提出策略的有效性。现有机制的分配方法性能最差，是因为现有机制倾向于给同一DC时隙分配同向请求，提升了碰撞发生概率。当卫星请求到达率超过8时，所有算法达到性能上限，对时隙的利用能力不再随请求的增加而提高。对于基于DQN的分配算法，再增加请求个数只会为了降低碰撞而不为新请求分配时隙；对于现有分配方法和随机选择，因为此时几乎所有时隙已经被分配完，再增加请求个数不会对结果造成影响。性能上限表明，当卫星请求到达个数超过8时，此时卫星应广播限制低重要性的请求发送频率，保证重要信息的传输顺畅。此外，每秒浮点数运算次数(floating point operations per second，FLOPS)反映神经网络算法对硬件性能的要求。目前市面上的DSP和FPGA的FLOPS大多为1~80 G。经统计，基于DQN的分配算法的单次运行所需浮点数运算次数为40 573，则运算用时小于1 ms，卫星硬件水平能够承受算法的时间开销。

4 结论

针对VDES多星座重复覆盖场景中的同频碰撞问题，本文提出了一种基于改进DQN的星座间兼容策略。基于VDES通信流程，通过设置船站作为卫星时隙资源感知节点，提升星座间的信息交互性。在此基础上提出一种基于改进DQN的时隙分配算法，将重构后的请求信息、历史时隙分配结果和当前子帧的时隙分配方案作为关键因素输入网络，获得时隙分配方案，并通过分配结果更新优化算法。仿真结果表明，提出的策略能够显著提高传输成功时隙数量。下一阶段的研究可以从重复覆盖率的动态变化入手，模拟真实场景中的卫星运动，为VDES协议的进一步完善提供建议。为实现工程化应用，在维持性能不变的同时，降低DQN参数精度和模型压缩以满足卫星的计算能力也是研究方向之一。