2. 中国科学院大学, 北京 100049;
3. 中国科学院空天信息创新研究院, 北京 100094
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing 100094, China
对地观测技术在环境和灾害的监测、林业的调查和保护、城市的建设和规划、资源勘探等领域发挥着越来越重要的作用[1]。对地观测卫星是一种空间成像资源[2-3],根据任务对地球表面目标的需求,利用星载传感器,在满足卫星成像条件的约束下,对地表目标进行观测并获取信息[4-6]。对地观测卫星任务规划的要素包括确定需要观测的目标、观测所需的卫星遥感器、观测开始时间和结束时间。在多卫星、多遥感器、多任务需求的情况下,如何分配卫星资源,高效完成任务,充分发挥对地观测卫星系统的能力,生成满意的卫星任务规划方案是非常重要的[7]。而在卫星任务的规划方案中,一个符合设计要求和理念的卫星轨道是任务高效执行的前提[8]。在对地观测卫星的轨道设计中,星下点轨迹优化问题是其中的一个重要内容。传统的星下点轨迹优化问题主要聚焦于无机动能力的星下点轨迹的优化,考虑的主要技术要求包括星下点轨迹重访、快速覆盖、最大覆盖时间等[9]。近年来,随着全球各国航天科技实力的增强,对地观测任务逐渐向具有多次轨道机动能力的多探测目标、多航天器协同的方向提升[10]。
目前,对地观测卫星的星下点轨迹计算的研究已经有很多。Zhu等[11]分析不同轨道数对星下点轨迹的影响,通过使用多颗在轨卫星对目标点进行观测,比较霍曼转移和双椭圆转移2种脉冲机动方法的差异。Zhang等[12]在J2摄动下研究切向脉冲对圆轨道星下点轨迹的影响,得到脉冲和经纬度变化关于时间的解析近似模型。Zhang等[13]提供了从初始轨道机动到最终经过观测目标的单共面脉冲和双共面脉冲机动的近似解析解。Zhang和Sheng[14]进一步研究对于经过目标点的指定最终轨道的共面三脉冲和四脉冲星下点轨迹调整的近似解析解,使其机动后的星下点轨迹经过指定地点,且消耗的燃料总量最小。本文在上述基础上发现,单一阶段的星下点轨迹设计在具备多次机动能力的对地观测任务中并不适用。因此研究出一种能够适用于多次机动能力的对地观测任务星下点轨迹描述方法以及轨迹拼接方法具有重要意义。
因此,本文提出一种基于标称轨道的星下点轨迹特征参数快速计算的方法,实现对星下点轨迹的间接解析,避开了复杂动力学模型下星下点轨迹的解析困难,也解决了数值积分带来的不可接受的时间等资源耗费问题。
1 问题描述本文题材来自第11届全国空间轨道设计竞赛。全国空间轨道设计竞赛(China Trajectory Optimization Competition,CTOC)是由中国力学学会和清华大学航天航空学院于2009年发起,面向航天轨道设计与优化工作的竞赛[15]。竞赛题目以正在规划中的或者将来可能实施的航天探测任务为背景,采用切实可行的工程参数和约束条件,对实际的航天探测任务具有重要的指导意义。本文以CTOC11赛题的任务1为背景,对对地观测卫星的星下点轨迹规划问题展开研究。
1.1 竞赛题目简介本文基于CTOC11赛题任务1的背景下开展研究。将任务及约束规定如下:观测任务由2颗观测卫星协同完成,一颗搭载光学相机,一颗搭载红外相机,简称为光学星和红外星。2颗观测星均采用化学推进系统,比冲为300 s,干重和燃料分别为300和250 kg。在初始时刻,设定2颗观测星位于轨道高度为350 km的圆轨道上,且二者的轨道倾角和升交点赤经相同。在任务时间内,观测星的飞行轨道以地球为中心天体,同时考虑J2摄动力和大气阻力的影响;在任意时刻,观测星的轨道高度均不得低于200 km,否则认为卫星坠毁,任务失败。观测星相邻2次脉冲机动的时间不得小于0.5 d,脉冲大小不得高于100 m/s。对于红外星,当卫星与目标点的视场角小于2.5°且卫星距离地表高度在200~500 km之间时,即视为完成了该目标点的观测成像;对于光学星,除满足上述约束外,还需要满足太阳高度角不得小于20°的约束条件才能完成目标点的观测成像。在满足约束的前提下,要求2颗遥感卫星在最短时间内,完成对200个地面点目标的准确观测。
考虑到不同的遥感载荷以及成像时的轨道高度对成像质量有所影响,因此引入单次得分指标s,s表达式如下
| $ s=C(5-0.01 h) . $ | (1) |
式中:h是成像时观测星的轨道高度,h∈[200, 500]km;C为相机系数,光学星观测时,C=1,红外星观测时,C=0.8。式(1)表明,在目标点观测成像时,观测星轨道高度应当尽量低,这也要求观测星应为低轨卫星。
在进行任务设计时,任务所要达到的最大化性能指标定义为
| $ W=\frac{1}{t_{\text {1end }}} \sum\limits_{i=1}^{200} \frac{s_i}{t_{\text {1end }} / 86\;400+\left(t_i / 86\;400\right)^2} . $ | (2) |
式中:W为任务得分;si为目标点i观测得分;ti为目标点i观测完成的时间,s;t1end为观测完最后1个目标点的时间,s。
1.2 动力学模型观测星在飞行过程中除受到地球引力之外,还受到地球非球形摄动和大气阻力摄动的影响。其中,地球非球形摄动仅考虑J2项摄动,大气阻力摄动采用1976标准大气模型。在地球赤道惯性坐标系(earth-centeved inertialframe,ECI)中,观测星动力学模型描述如下
| $ \ddot{{\boldsymbol{r}}}=-\frac{\mu}{r^3} {\boldsymbol{r}}+{\boldsymbol{a}}_{\mathrm{J}}+{\boldsymbol{a}}_{\mathrm{d}} . $ | (3) |
式中:μ为地球引力常数,其值为398 600.441 5 km3/s2;r为观测星位置矢量大小,r =[x, y, z]T;aJ和ad分别为J2项摄动和大气阻力摄动,aJ和ad表达式如下
| $ \left\{\begin{array}{c} {\boldsymbol{a}}_{\mathrm{J}}=1.5 \mu J_2 R_{\mathrm{E}}^2\left[\begin{array}{c} 5 x z^2-r^2 x \\ 5 y z^2-r^2 y \\ 5 z^3-3 r^2 z \end{array}\right] / r^3, \\ {\boldsymbol{a}}_{\mathrm{d}}=-\frac{1}{2} C_{\mathrm{d}} \rho\left(\frac{S}{m}\right)\left\|{\boldsymbol{v}}_R\right\| {\boldsymbol{v}}_R , \\ {\boldsymbol{v}}_R=\dot{{\boldsymbol{r}}}-\omega_{\mathrm{E}}[y, -x, 0]^{\mathrm{T}}. \end{array}\right. $ | (4) |
式中:J2为J2项摄动系数,其值为1.082 626 9×10-3;RE为地球半径,其值为6 378.137 km;Cd为大气阻力系数,其值为2.2;S为观测星迎风截面积,其值为8 m2;ρ为大气密度(采用美国标准大气1976模型);m为观测星质量;ωE为地球自转角速率,其值为7.292 115 855 3×10-5 rad/s;vR为观测星质心与当地大气的相对速度矢量。
观测星采用大推力的化学推进系统,机动过程近似为瞬时速度脉冲,速度脉冲的方向不受限制。施加速度脉冲前后,观测星质量分别记为m-和m+,m-和m+的函数关系如下
| $ m_{+}=m_{-} \exp \left(-\frac{\Delta v}{g_0 I_{\mathrm{sp}}}\right). $ | (5) |
式中:Δv为速度脉冲大小;g0为地球海平面重力加速度,其值为9.806 65 m/s2;Isp为发动机比冲,其值为300 s。
2 基于特征参数拟合的星下点轨迹规划方法由于离散变量和连续变量的耦合是一个复杂的组合优化问题,很难利用现有数学方法进行分析求解。因此采用“先全局寻优、再局部搜索”的求解策略,即先设计一种轨道转移近似解析模型进行全局寻优,得到轨道机动大致矢量信息和时间点,以此为初值再对各段轨道段的机动脉冲与转移时间进行局部搜索得到精确解。
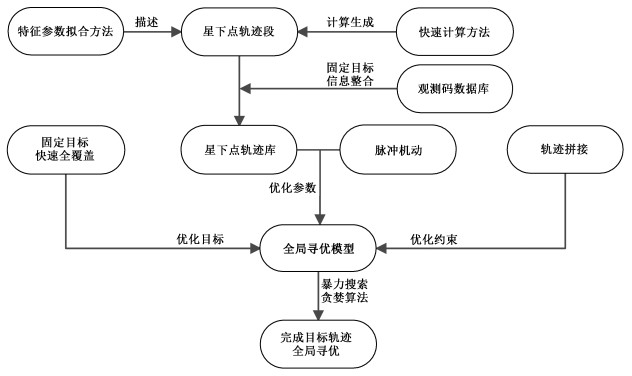
本文所采用全局寻优方法以脉冲为分割点,对每次机动前后的轨迹进行分段设计,再以脉冲作为优化变量进行轨迹拼接,从而构成优化模型,根据观测目标制定相应的优化指标进行全局寻优。在对轨迹段的设计过程中,首先采用特征参数拟合方法对星下点轨迹进行描述,并据此建立星下点轨迹的快速计算方法;其次根据固定目标点建立观测码数据库,建立固定目标点与星下点轨迹之间的联系;最后,通过统计整理的方法将固定目标点信息整合到星下点轨迹库。在完成轨迹段的分段设计后,构建全局寻优模型,采用穷举法获得星下点轨迹规划的最优解。星下点轨迹规划的全局寻优方法算法流程图如图 1所示。
|
Download:
|
| 图 1 星下点轨迹规划的全局寻优方法算法流程图 Fig. 1 Global optimization algorithm flow chart of trajectory planning on the ground tracks of satellite | |
本文所涉及的动力学模型考虑了J2项摄动和大气阻力摄动,直接采用数值递推方法对轨道设计需要耗费大量的计算资源和时间,且目前尚没有能够达到精度要求的综合2种摄动的瞬时位置矢量解析解。为了对星下点轨迹进行描述以及快速计算,本节对完整描述星下点轨迹所需的要素进行分析,并进一步分析对星下点轨迹具有显著影响和作用的特征参数。
星下点的经纬度信息,可由ECI的卫星位置信息转换到地球固连坐标系(earth-centered, earth-fixed,ECEF)下,如下式所示,再通过ECEF与经纬高模型(λ, ϕ, h)之间的关系计算得到。
| $ {\boldsymbol{r}}_{\mathrm{ECEF}}={\boldsymbol{R}}_z\left(\alpha_{\mathrm{G}}\right) {\boldsymbol{r}}_{\mathrm{ECI}} . $ | (6) |
式中:Rz(αG)为从ECI到ECEF的转换矩阵
| $ {\boldsymbol{R}}_z\left(\alpha_{\mathrm{G}}\right)=\left[\begin{array}{ccc} \cos \alpha_{\mathrm{G}} & \sin \alpha_{\mathrm{G}} & 0 \\ -\sin \alpha_{\mathrm{G}} & \cos \alpha_{\mathrm{G}} & 0 \\ 0 & 0 & 1 \end{array}\right] . $ | (7) |
式中:αG表示某一时刻的格林尼治平恒星时。
已知卫星在ECEF下的位置矢量rECEF=[xECEF, yECEF, zECEF]T,则经度λ和纬度ϕ的计算公式如下
| $ \lambda=\arctan \left(\frac{y_{\mathrm{ECEF}}}{x_{\mathrm{ECEF}}}\right), \quad \phi=\arcsin \left(\frac{y_{\mathrm{ECEF}}}{\left\|r_{\mathrm{ECEF}}\right\|}\right) . $ | (8) |
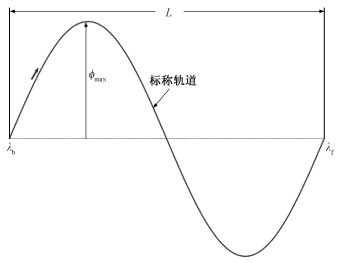
地球卫星星下点轨迹由轨道运动、地球自转及摄动等因素决定。本文假设地球自转角速度恒定,则影响星下点轨迹的主要因素是轨道参数。轨道参数主要有半长轴a,偏心率e,倾角i,升交点赤经Ω,近地点幅角ω和真近点角θ。其中θ主要表征卫星的时间信息,其他5个参数则主要表征卫星的轨道空间信息。a、e、i、Ω、ω的改变均会引起星下点轨迹的变化[16],且由于这5个轨道参数相互独立,因此这5个轨道参数是影响星下点轨迹的主要因素。根据竞赛题目要求可知,观测卫星在整个观测任务期间,均位于低轨。在低轨问题中,由于e为小量,可将e和ω近似为常值0。因此,仅需3个要素即可描述低轨卫星的星下点轨迹。低轨卫星星下点轨迹3要素的确定方法如下。首先,根据任务要求初选1条标称轨道,标称轨道考虑了J2项摄动和大气阻力摄动,是一条真实状态的轨道。标称轨道以赤道升交点作为起点,在式(3)所示动力学模型中进行数值积分,当观测星到达赤道降交点时终止。记标称轨道的始末时刻分别为tb和tf。在tb时刻,观测星质量为m,瞬时轨道半长轴、偏心率、倾角、升交点赤经、近地点幅角和真近点角依次为a、e、i、Ω、ω和θ(θ=-ω)。观测星在tb和tf时刻的星下点纬度均为0°,经度分别为λb和λf,λb和λf的差记为L(L=λf-λb)。记星下点纬度的极大值为ϕmax,如图 2所示。星下点轨迹仅由λb、λf(或L)和ϕmax这3个要素即可确定。
|
Download:
|
| 图 2 标称轨道星下点轨迹参数 Fig. 2 Parameters of the ground tracks of satellite under the nominal orbit | |
在由3要素表征的标称星下点轨迹的基础上,为了研究摄动与航天器机动对整条星下点轨迹的影响,需要对标称轨道星下点轨迹进行完整的记录。在时间区间[tb, tf]内,以0.1 s为时间间隔记录观测星星下点轨迹数据,数据格式如表 1所示。表 1中,t为数据时刻,λ为经度,ϕ为纬度,h为地表高度。
|
|
表 1 标称轨道星下点轨迹数据列表 Table 1 The ground track data of satellite under the nominal orbit |
在本次轨道设计的过程中,摄动引起的星下点轨迹改变主要体现为长期影响,而脉冲机动引起的星下点轨迹改变为即时性的改变。因此此处以J2和大气摄动下的星下点轨迹为标称轨迹,分析脉冲机动对星下点轨迹的影响。
观测星在一次幅值不超过100 m/s的脉冲后,受到影响的参数有半长轴a、偏心率e、轨道倾角i、升交点赤经Ω、近地点幅角ω、真近点角θ、质量m。由于本文假设标称轨道的星下点轨迹从赤道升交点处出发,因此出发点的纬度幅角为0°,即要求θ=-ω。由于脉冲幅值的限制,i和Ω的改变量为小量[17],此处忽略其影响。随着半长轴a、偏心率e、近地点幅角ω、质量m的改变,星下点轨迹参数L和ϕmax也可能会随之改变。因此下文分别分析4个自变量a、e、ω、m的小幅变化与2个因变量L、ϕmax之间的关系。
记tb时刻a、e、ω、m的改变量分别为Δa、Δe、Δω、Δm。每一个变量的改变所引起的L的变化分别记为ΔLa、ΔLe、ΔLω、ΔLm,函数关系式分别记为f(Δx)(x依次为a、e、ω、m);每一个变量的改变所引起的ϕmax的变化量分别为Δϕa、Δϕe、Δϕω、Δϕm,函数关系式分别记为g(Δx)(x依次为a、e、ω、m)。具体表达形式如下式所示:
| $ \left\{\begin{array}{l} \Delta L=f(\Delta a, \Delta e, \Delta \omega, \Delta m), \\ \Delta L_a=f(\Delta a, 0, 0, 0), \\ \Delta L_e=f(0, \Delta e, 0, 0), \\ \Delta L_\omega=f(0, 0, \Delta \omega, 0), \\ \Delta L_m=f(0, 0, 0, \Delta m) . \end{array}\right. \left\{\begin{array}{l} \Delta \phi=g(\Delta a, \Delta e, \Delta \omega, \Delta m) , \\ \Delta \phi_a=g(\Delta a, 0, 0, 0), \\ \Delta \phi_e=g(0, \Delta e, 0, 0), \\ \Delta \phi_\omega=g(0, 0, \Delta \omega, 0), \\ \Delta \phi_m=g(0, 0, 0, \Delta m). \end{array}\right. $ | (9) |
下面通过一个一般算例分析4个相关参数对f(Δx)和g(Δx)的影响效果。给定一条标称轨道:在起始时刻tb标称轨道参数及变化范围如表 2所示。4个作为自变量的参数根据一次幅值不超过100 m/s的脉冲引起的改变设定取值改变范围。
|
|
表 2 tb时刻标称轨道参数及其取值改变范围 Table 2 Nominal orbit parameters at time tb and their range of value change |
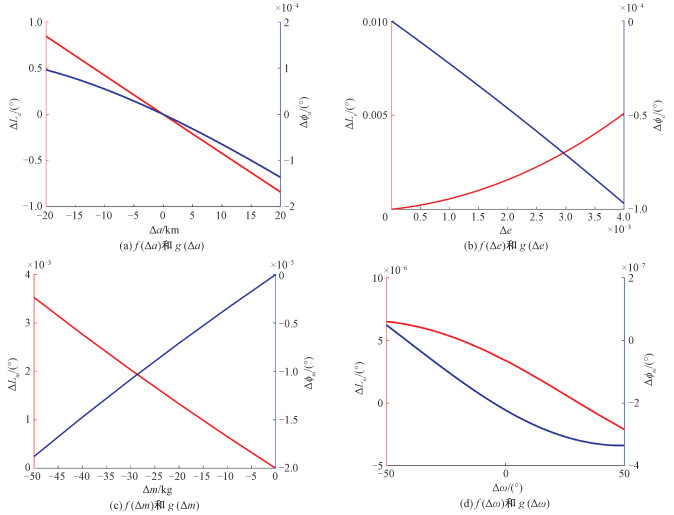
在表 2所示的算例中,f(Δx)和g(Δx)的函数曲线如图 3所示。
|
Download:
|
| 图 3 f(Δx)和g(Δx)的函数曲线对比图 Fig. 3 The function curves of f(Δx) and g(Δx) | |
由图 3可见,g(Δx)在取值范围内均为小量,因此Δa、Δe、Δω和Δm对ϕmax的影响可忽略不计。f(Δx)在4个参数下存在不同表现,相比Δe、Δω和Δm而言,Δa引起的变化特别显著,因此是改变L的主要因素。因此下文以L作为星下点轨迹设计的特征参数,且忽略轨道机动改变e、ω和m对L的影响,以Δa作为L设计的唯一因素。
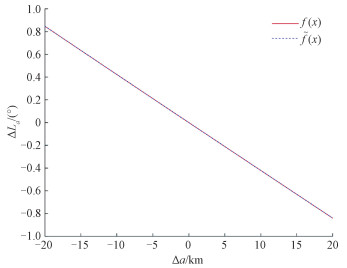
为进一步对设计过程和计算量进行简化,本文采用一种基于标称轨道的星下点参数拟合方法对星下点轨迹进行拟合。具体而言将采用3次多项式函数对f(Δa)进行拟合,拟合函数记为
|
Download:
|
|
图 4 f(Δa)和 |
|
由图 4曲线的数据分析,函数曲线f(Δa)与拟合函数曲线
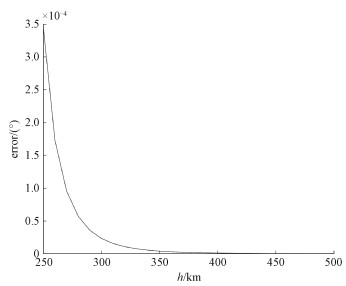
在此基础上,通过对250~500 km内不同轨道高度的近圆轨道算例进行仿真,可以得到拟合最大绝对误差均在0.000 5°以下,如图 5所示,轨迹误差小于1 ‰。
|
Download:
|
| 图 5 不同高度的标称轨道采用拟合方法带来的最大绝对误差变化图 Fig. 5 The maximum absolute error variation diagram of nominal orbits at different heights by fitting method | |
而250~500 km内,对于一个半锥角为2.5°的观测载荷,其在地面所成的圆形视场覆盖半径所对应的地心角最小值为0.098 1°,即覆盖范围至少跨越经度为0.196 1°,地心角ψ计算如下所示
| $ \tan \psi=\frac{h \cdot \tan 2.5^{\circ}}{R_{\mathrm{E}}}. $ | (10) |
因此,拟合误差的量级小于观测视场成像区域量级的1 %,即可判断拟合误差带来的轨迹偏离对视场成像区域的干扰效果很小。在轨道设计时,通常认为,对于轨迹误差小于1 ‰或成像区域的误差小于1 % 是可以接受的。因此可认定特征参数的拟合效果足够好,能够应用于星下点轨迹的近似解析模型,而拟合带来的近似解析模型误差,可以通过对大致解的局部搜索获得精确解来消除。由不同仿真工况可以得到,本文所采用的特征参数拟合方法,对轨道高度在250~500 km范围内的近圆轨道均有效。对于更高的轨道高度,需要考虑更换动力学模型并重新设计仿真,因此不在设计范围之内。
基于以上分析,本文遴选λb和L作为观测星轨道星下点轨迹的设计参数。在设计过程中,通过在升交点处施加轨道机动、改变Δa来调整L,达到使特定地面目标进入卫星观测视场的目的;采用特征参数拟合的方法对星下点轨迹进行拟合,达到对星下点轨迹快速计算的目的。
2.2 星下点轨迹的快速计算方法本节考虑在升交点施加轨道机动后,星下点轨迹如何计算的问题。
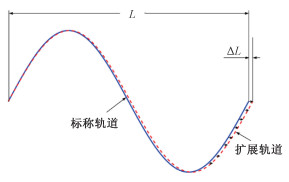
如2.1节所述,Δa是影响L的主要因素,所以本文选择Δa作为设计L的唯一因素。记L的改变量为ΔL。根据2.1节的分析,如图 6所示,Δa对星下点轨迹的影响描述如下:在任意时刻t,星下点纬度和卫星高度均不变,但是经度发生了变化。记经度改变量为ΔLt。由于Δa的取值范围相对a而言是高阶小量,相应的ΔL相比L而言也是高阶小量。因此本文假设ΔLt随时间线性变化,ΔLt在下一个升交点处取得最大值ΔL。ΔLt与时间的关系如下
| $ \gamma=\left(t-t_{\mathrm{b}}\right) /\left(t_{\mathrm{f}}-t_{\mathrm{b}}\right), $ | (11) |
| $ \Delta L_t=\gamma \cdot \Delta L. $ | (12) |
|
Download:
|
| 图 6 Δa对星下点轨迹的影响示意图 Fig. 6 Schematic diagram of the influence of Δa on the ground tracks of satellite | |
经过上述分析和计算,即可得到参数拟合后的星下点轨迹。考虑到观测星相邻2次机动的最短时间间隔为0.5 d,将观测星相邻2次穿越升交点的飞行轨道记为1圈,则观测星无机动下飞行8圈后才能施加机动。下面将对完整的8圈星下点轨迹快速计算以统一的形式表出。
首先,对给出的标称轨道进行轨道积分,得到完整的单圈标称星下点轨迹,如表 1所示,其第j行数据以[tj, λj, ϕj, hj]标出;然后,在观测星所做出的1次机动后,根据式(11)和式(12)计算得到机动后的单圈特征参数拟合星下点轨迹,其第j行数据以[t1, j, λ1, j, ϕ1, j, h1, j]标出;最后,在单圈特征参数拟合星下点轨迹的基础上,计算得到其在第i(i=1, 2, …, 8)圈的轨道星下点数据,第i圈第j行数据以[ti, j, λi, j, ϕi, j, hi, j]标出。ti, j, λi, j, ϕi, j和hi, j的计算公式如下
| $ \left\{\begin{array}{l} t_{i, j}=(i-1)\left(t_{\mathrm{f}}-t_{\mathrm{b}}\right)+t_{1, j}, \\ \lambda_{i, j}=(i-1) L+(\gamma+i-1) \Delta L+\lambda_{1, j}, \\ \phi_{i, j}=\phi_{1, j}, \\ h_{i, j}=h_{1, j}+2 \Delta a-|2 \gamma-1| 2 \Delta a . \end{array}\right. $ | (13) |
本节主要探讨观测一个固定地面目标点星下点轨迹所需达到的条件。
为便于分析,引入观测码的概念,一个固定地面目标的观测码指的是能够观测到该固定地面目标的卫星星下点轨迹参数组合。观测码由一条卫星星下点轨迹穿过固定地面目标点的轨迹参数[λb, L, ϕmax]以及该轨迹略微偏移但能保证目标点在观测范围内的偏移误差参数ε组成。由于ϕmax在卫星运行过程中几乎不发生改变,因此后续观测码省略ϕmax,即以[λb, L, ε]表示一个观测码。
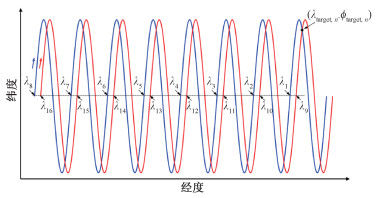
在本文的观测任务中,有200个固定于地面的目标点。将第n(n=1, 2, …, 200)个固定目标点的经纬度分别记为λtarget, n和ϕtarget, n。根据脉冲机动间隔要求,每2次脉冲机动不得小于0.5 d,因此本文设定观测星轨道每经过8圈无机动飞行后就在赤道升交点处进行1次轨道机动。对于任意一个固定的固定地面目标点,其可能被观测星在8圈星下点轨迹中的任意一圈覆盖,且存在星下点轨迹上升段覆盖和星下点轨迹下降段覆盖2种情况。因此,对于一个给定的L,任意固定目标点均存在16个观测码,其对应的λb依次记为λi(i=1, 2, …, 16),如图 7所示。
|
Download:
|
| 图 7 任意目标点的16条观测轨道示意图 Fig. 7 Schematic diagram of 16 observation orbits about any target point | |
λi计算过程描述如下:首先,在表 1所示的标称轨道星下点轨迹数据列表的纬度列中,查找到ϕtarget, n所在区间。由于穿越一条纬度线存在升交点与降交点,因此查表时存在2个区间,一个为轨迹上升段,一个为轨迹下降段,提取每个区间两端数据。然后,采用线性插值方法计算得到星下点轨迹上升穿越纬度ϕtarget, n的时刻tas、经度
| $ \lambda_i=\left\{\begin{array}{l} \lambda_{{\text {target }}, n}-\left(\hat{\lambda}_{\text {des }}-\lambda_0\right)-(i-1) L, \\ \quad i=1, 2, \cdots, 8, \\ \lambda_{{\text {target }}, n}-\left(\hat{\lambda}_{\mathrm{ds}}-\lambda_0\right)-(i-9) L, \\ i=9, 10, \cdots, 16 . \end{array}\right. $ | (14) |
式中:λ0为表 1标称轨道星下点轨迹数据列表中起始时刻的经度。
按照观测码的生成计算方式,通过遍历n和i的取值,即可得到该L取一个特定值时的所有固定目标点观测码。此外,考虑到观测星成像角度允许存在2.5°的误差,因此,存在星下点轨迹略微偏移但能保证目标点在观测范围内的情况,该偏移误差量记为ε,因此能够观测到某个固定目标点的实际λi取值为[λi-ε1, λi+ε2]。考虑到ε1和ε2近似相等,本文设定ε1和ε2均取值为ε。下面介绍ε的计算过程。
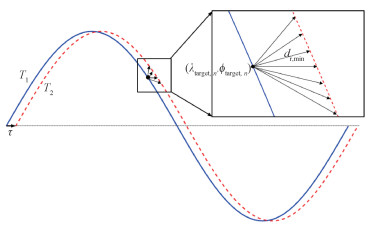
如图 8所示,将一个经过第n个固定目标点的观测星轨道星下点轨迹记为T1(蓝色实线),T1沿经度方向整体平移τ角度后的轨迹记为T2。在ECEF坐标系中,T2的点在三维空间上与固定目标点(λtarget, n, ϕtarget, n)的相对距离记为dr。在T2上寻找dr的极小值,记为dr.min。根据dr.min可计算得到ε,ε计算公式如下
| $ \varepsilon=\frac{d_{{\mathrm{r}} . \min }}{\hat{h} \tan \left(2.5^{\circ}\right)} \tau. $ | (15) |
|
Download:
|
| 图 8 观测星轨道偏移覆盖固定地面目标点示意图 Fig. 8 Schematic diagram of observation satellite orbit offset covering fixed ground target | |
至此,可以得到固定目标点的观测码数据库列表,如表 3所示。表 3中,No为固定目标点编号,λb为观测星星下点轨迹穿过编号为No的目标时起始轨道的星下点经度,L为对应的星下点轨迹始末时刻经度差,ε为观测编号为No的目标时允许的λb最大偏移误差。
|
|
表 3 固定目标点的观测码数据库列表 Table 3 Fixed target point observation code database |
在本节中,将分2步对星下点轨迹进行规划设计。第1步,从观测码数据库入手,分析出任意一条星下点轨迹所能观测到的固定地面目标点,形成星下点轨迹数据库。第2步,以每次与中继星进行数据传输作为分割点,以多个无动力飞行轨道段和轨道段间的脉冲为优化变量建立目标轨迹全局寻优模型。
在2.3节中,从固定目标点的角度分析,建立主要体现固定目标点与λb关系的观测码数据库。为便于实现后续的轨迹拼接,需要转换视角,从星下点轨迹的角度考虑星下点轨迹与固定目标点的关系。因此,需要对表 3中固定目标点的观测码数据库进行统计整理,获得与之呈逆映射关系的轨迹数据库。
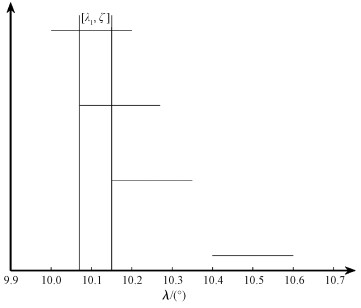
根据表 3固定目标点的观测码数据库,可以通过确定起始升交点经度λ1和首尾经度差L,对观测码数据库查表,直接获得任意一条标称轨道下的8圈无动力星下点轨迹所能够观测到的所有固定目标点。因此,在L确定的情况下,可以通过遍历起始经度λ1,获得所有不同起始经度下的星下点轨迹能够观测的目标点数据。如图 9所示,所有观测码依据λb-ε从左上至右下依次列出,横坐标为相应的经度,纵坐标仅起排序作用,无实际意义,观测码宽度为2ε。根据图 9中的信息进行分析,对能够观测到相应目标点的起始经度范围,以[λ1, ξ]表示该范围。λ1为起始经度范围的中间值,ξ为起始经度范围的半宽度,即为允许的λ1最大误差。
|
Download:
|
| 图 9 观测相应目标的起始经度范围确定过程示意图 Fig. 9 Schematic diagram of determining the initial longitude range of the corresponding target | |
通过对表 3和图 9的统计整理,可以得到标称轨道下的8圈轨迹数据库,如表 4所示。表 4中,第1列为序列号,λ1为起始升交点经度,λ2为8圈轨道终端的升交点经度,ξ为观测相应编号的目标时允许的λ1最大误差,num为观测目标点个数,Noi(i=1, 2, …)分别为观测目标点的编号。轨迹库内包含了任意一条星下点轨迹所能观测到的地面目标点信息。
|
|
表 4 标称轨道下的8圈轨迹数据库 Table 4 Database of 8-loop trajectories under a nominal orbit |
表 4展示了标称轨道下的8圈轨迹数据库,单圈首尾经度差L为定值。而实际卫星运行中,并不总是遵循标称轨道而运动。在2.1节的分析中,本文已经确定了Δa是改变L的主要因素。因此将轨道半长轴a的变化Δa加入考虑,即可获得包含所有情况的8圈轨迹数据库。在标称轨道上,即Δa的值为0。
8圈轨迹数据库的分析计算过程如下。首先,在标称轨道的基础上,以da为间隔在区间[-Δamax, Δamax]上遍历Δa取值,计算相应的L。其中,da和Δamax需要根据观测任务所处的阶段而定;然后,根据不同的L重新计算相应的固定目标点观测码数据库;最后,对所有固定目标点观测码数据库分别统计整理,生成半长轴为a+Δa的轨道的8圈轨迹数据库,如表 5所示。
|
|
表 5 任意轨道下的8圈轨迹数据库 Table 5 Database of 8-loop trajectories under any nominal orbit |
上述分析完成了星下点轨迹规划中的第1步,即得到了任意一条星下点轨迹所能观测到的固定地面目标点。第2步,以每次与中继星进行数据传输作为分割点,以多个无动力飞行轨道段和轨道段间的脉冲为优化变量建立目标轨迹全局寻优模型。
在拼接多段轨道段的过程中,需要通过脉冲对多个无动力飞行轨道段进行拼接。拼接过程中,轨迹规划模型为:1)指标:观测目标点个数最大化;2)参数:各个轨道段的起始经度λi和首尾经度差Li(i=1, 2, …);3)约束:λi+8Li=λi+1,并且要求观测相应目标点。
根据轨迹规划模型对多轨迹段进行拼接,继而进行全局寻优。在本文所设计的一系列方法下,已经完成了对解空间的剪枝,解空间大大缩小,最终以暴力搜索结合贪婪搜索的方法即可完成对目标轨迹全局寻优。在采用全局寻优获得轨迹转移近似解析解后,得到轨道机动大致矢量信息和时间点,以此为初值再对各段轨道段的机动脉冲与转移时间进行局部搜索得到精确解。
至此,本节完成了星下点轨迹规划设计过程的介绍。完成一轮目标观测后,与中继星进行数据传输,再进行下一轮的目标观测,依次完成整个大规模地面目标快速观测任务。
3 数值仿真分析根据赛题要求,任务的初始时刻设定在UTC 2020年1月1日0时。在初始时刻,2颗观测星被设定位于轨道高度为350 km的圆轨道上,且两者的轨道倾角和升交点赤经相同。因此半长轴和偏心率已经被给定,而圆轨道下近地点幅角没有意义,因此需要设计的初始时刻轨道参数为轨道倾角i、升交点赤经Ω、光学星真近点角θop、红外星真近点角θin。其中i和Ω的设计影响到轨道面的状态,为主要设计参数。
3.1 轨道倾角i由于J2项摄动和大气阻力摄动不改变观测星轨道倾角,且改变轨道倾角需要较多速度脉冲,因此本文认为一旦给定观测星初始轨道倾角,则在任务时间内观测星轨道倾角固定不变。同时,由于轨道倾角i直接决定星下点轨迹的最高纬度,结合赛题数据来看,200个固定目标点的最大纬度绝对值为64.1°,因此得到结论:倾角i的取值范围为[64.1°, 115.9°]。基于这个取值范围,本文考虑3种典型方案:1)顺行轨道i的最小值64.1°;2)最大程度利用光学星,太阳同步轨道96.59°;3)逆行轨道i的最大值115.9°。
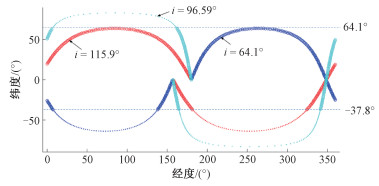
为了对3种方案进行评价,本文引入有效经度跨度作为评价指标。有效经度跨度是指在一个轨道周期内,观测星穿越目标区域的所有弧段经度长度总和。在本次任务中,根据200个固定的纬度统计,目标区域为纬度[-37.8°, 64.1°]。假定观测星轨道半长轴为6 728 km,e、Ω、ω和θ均为0,则i分别为64.1°、96.59°和115.9°时,有效经度长度如图 10所示。图中,‘ ·’表示星下点轨迹,‘。’表示有效经度点。
|
Download:
|
| 图 10 3种方案的有效经度跨度 Fig. 10 The effective longitude span of the three schemes | |
由图 10可见:i分别64.1°、96.59°和115.9°时,有效经度长度分别为206.73°、49.2°和240.3°;这表明:当i为115.9°时,有效经度长度最长,即在相同时间内,观测到目标点的概率更高。因此,本文选定观测星初始轨道倾角i为115.9°。
3.2 升交点赤经Ω为在最短时间内完成全覆盖观测任务,需要最大程度地利用光学星,即维持符合太阳高度角约束的时间尽量长,因此太阳位置矢量应当尽量位于光学星轨道面内。太阳矢量位置仅与地球公转有关,为长周期因素而J2项摄动使得观测星Ω随时间增大而递增,即J2项摄动导致光学星轨道面随时间发生变化,因此需要探究Ω变化对光学星工作能力的影响。在J2项摄动,Ω的平均变化率计算公式如下
| $ \dot{\varOmega}=-\frac{3}{2} \sqrt{\frac{\mu}{a^3}} \frac{R_{\mathrm{E}}^2 {\mathrm{~J}}_2}{a^2\left(1-e^2\right)^2} \cos i . $ | (16) |
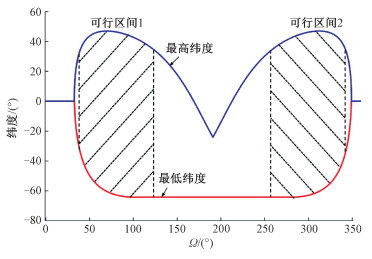
采用一个简单算例研究Ω变化对光学星工作能力的影响。设定在初始时刻,a=6 728 km,i为115.9°,e和ω均为0,则遍历真近点角θ(θ∈[0, 360°))取值,光学星能够观测到的最高纬度和最低纬度与Ω的函数关系如图 11所示。
|
Download:
|
| 图 11 光学星观测到最高纬度和最低纬度随升交点赤经的变化图 Fig. 11 The changes of the highest and lowest latitudes with the ascending intersection of right ascension observed by optical satellites | |
由图 11可知,光学星在较大范围的Ω内均具有一定的工作能力,当Ω取值如图 11算例下的两端值时完全丧失工作能力。由于要求光学星工作能力尽可能高,因此上述算例下Ω具有2个可行取值区间,如斜线区域所示。
预先假设任务1的完成时间为20 d,则Ω增加大约72°。为使得在20 d内,光学星能够最大程度观测到固定目标点所在区域,且早期观测的最高纬度尽量大,因此本文选定Ω的第1个可行区间,且取值范围选为Ω∈[40°, 45°]。
3.3 真近点角θop、θin考虑到真近点角决定的是观测星在轨道上的位置,直接决定了观测星出发后第1个观测轨道段的观测质量。因此,光学星真近点角θop和红外星真近点角θin直接结合在观测星出发后第1个观测轨道段中进行设计优化。
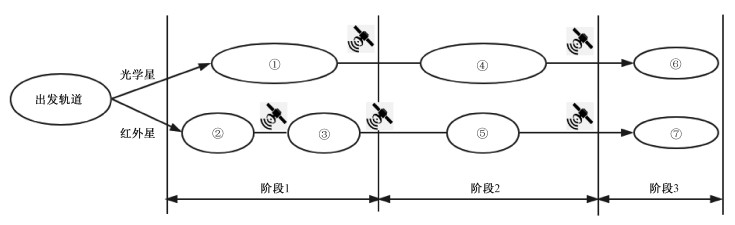
3.4 观测轨道段的规划设计在星下点轨迹规划一节中,本文给出了一个完整观测轨道段,即从观测目标为0到观测目标达到预期个数而与中继星进行数据传输的星下点轨迹规划方法。在本节中,本文将对所有观测轨道段进行规划设计从而完成整个大规模地面目标短时覆盖观测任务。本文将任务在观测星从出发轨道出发后分为3个部分,如图 12所示。
|
Download:
|
| 图 12 观测轨道段的规划设计流程图 Fig. 12 Flow chart of planning and design of observation orbit segment | |
阶段1:此阶段根据式(2),以得分为目标,应在较短的时间内取得较多的分,因此轨道高度应较低,同时考虑到地面目标大部分位于北半球,因此将近地点设定在北半球上空。该部分的标称轨道设计为轨道远地点高度ha=350 km、近地点高度hp=210 km、近地点幅角ω=90°。设计结果为:光学星完成了1次观测轨道段任务、红外星完成了2次观测轨道段任务,并完成中继。
阶段2:此阶段主要考虑得分因素中的t1end,因此抬高远地点,增加视场范围,增大观测概率。该部分的标称轨道设计为轨道远地点高度ha≥400 km以上,近地点高度hp≥210 km,近地点幅角ω=90°。设计结果为:光学星和红外星各完成了1次观测轨道段任务,并完成中继。
阶段3:此阶段为完成任务阶段,为尽快完成任务,抬高轨道高度,并且凭借机动能力,迅速覆盖剩余的所有目标。该部分的标称轨道设计为轨道远地点高度ha≥400 km,近地点高度hp≥400 km,近地点幅角不做要求。设计结果为:光学星和红外星各完成了1次观测轨道段任务,第3阶段观测完毕所需的中继耗时不需要计入任务得分要求,在此不加分析。
完成轨道段的规划设计后,进行仿真,各个观测轨道段的各项指标如表 6所示,观测轨道段的编号如图 12所示,总耗时包括了各个观测轨道段所需的中继耗时,其中两颗观测星各自的最后一个观测轨道段除外。
|
|
表 6 各个轨道段的各项指标 Table 6 Indicators of each track segment |
经过上述观测轨道段的规划设计和仿真,整个大规模地面目标快速全覆盖观测任务全部完成。整个任务最终耗时19.19 d,总得分352.49分。该结果验证了基于特征参数拟合的星下点轨迹快速计算和星下点轨迹规划方法的有效性和高效性。
4 结论针对第11届全国空间轨道设计竞赛提出的面向大规模地面目标复杂任务的双星轨道设计与机动优化问题,提出基于特征参数拟合的星下点轨迹快速计算方法,采用数据库与轨迹拼接优化方法结合的星下点轨迹规划方法,实现了大规模地面目标快速覆盖观测的任务。通过对特征参数的分析,减少了变量数目,降低了计算维度。基于特征参数拟合的星下点轨迹建模方法,实现了对星下点轨迹的间接解析,避开了复杂动力学模型下星下点轨迹的解析困难,也解决了数值积分带来的不可接受的时间等资源耗费问题。采用特征参数拟合方法计算得到的星下点轨迹,与实际轨迹最大绝对误差小于0.000 1°,最大相对误差小于10-4。为了建立优化模型,本文通过建立观测码的方法将地面目标整合到观测码数据库中,并进一步转化为轨迹拼接所需的星下点轨迹数据库,实现了优化参数、优化约束、优化指标齐备的优化模型。本文在上述方法的基础上,综合运用了降维设计、化大规模变量空间为数据库、暴力搜索等策略的全局优化方法以及一些合适的局部优化方法,从而构建了整个大规模地面目标快速覆盖的解决方案,解决了大规模地面目标短时覆盖观测问题。仿真结果表明,本文所采用的设计方法和方案能够在19.19 d内,以352.49分的观测指标完成该任务。本文提出的基于特征参数拟合的多地面目标星下点轨迹规划方法,可用于各类近圆轨道的星下点轨迹设计问题。
| [1] |
龚威, 史硕, 陈必武, 等. 对地观测高光谱激光雷达发展及展望[J]. 遥感学报, 2021, 25(1): 501-513. |
| [2] |
Liu X L, Laporte G, Chen Y W, et al. An adaptive large neighborhood search metaheuristic for agile satellite scheduling with time-dependent transition time[J]. Computers & Operations Research, 2017, 86: 41-53. Doi:10.1016/j.cor.2017.04.006 |
| [3] |
Xu R, Chen H P, Liang X L, et al. Priority-based constructive algorithms for scheduling agile earth observation satellites with total priority maximization[J]. Expert Systems With Applications, 2016, 51: 195-206. Doi:10.1016/j.eswa.2015.12.039 |
| [4] |
Qi J T, Guo J J, Wang M M, et al. A cooperative autonomous scheduling approach for multiple earth observation satellites with intensive missions[J]. IEEE Access, 2021, 9: 61646-61661. Doi:10.1109/ACCESS.2021.3075059 |
| [5] |
Wang S, Zhao L, Cheng J H, et al. Task scheduling and attitude planning for agile earth observation satellite with intensive tasks[J]. Aerospace Science and Technology, 2019, 90: 23-33. Doi:10.1016/j.ast.2019.04.007 |
| [6] |
Barkaoui M, Berger J. A new hybrid genetic algorithm for the collection scheduling problem for a satellite constellation[J]. Journal of the Operational Research Society, 2020, 71(9): 1390-1410. Doi:10.1080/01605682.2019.1609891 |
| [7] |
陈昊, 赵斐, 白建东. 对地观测卫星动态任务调度优化算法研究[J]. 无线电工程, 2021, 51(9): 947-954. Doi:10.3969/j.issn.1003-3106.2021.09.016 |
| [8] |
原斌. 对地观测卫星轨道设计及振动控制[D]. 沈阳: 沈阳航空航天大学, 2017.
|
| [9] |
付晓锋. 空间快速响应任务中的轨道设计问题研究[D]. 长沙: 国防科学技术大学, 2012.
|
| [10] |
甘岚, 龚胜平. 机动卫星星座对多目标成像任务规划[J]. 清华大学学报(自然科学版), 2021, 61(3): 240-247. Doi:10.16511/j.cnki.qhdxxb.2020.26.013 |
| [11] |
Zhu K J, Li J F, Baoyin H X. Satellite scheduling considering maximum observation coverage time and minimum orbital transfer fuel cost[J]. Acta Astronautica, 2010, 66(1/2): 220-229. Doi:10.1016/j.actaastro.2009.05.029 |
| [12] |
Zhang J, Li H Y, Luo Y Z, et al. Effects of in-track maneuver on the ground track of near-circular orbits[J]. Journal of Guidance, Control, and Dynamics, 2014, 37(4): 1373-1378. Doi:10.2514/1.G000047 |
| [13] |
Zhang G, Cao X B, Mortari D. Analytical approximate solutions to ground track adjustment for responsive space[J]. IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(3): 1366-1383. Doi:10.1109/TAES.2016.140644 |
| [14] |
Zhang G, Sheng J. Impulsive ground-track adjustment for assigned final orbit[J]. Journal of Spacecraft and Rockets, 2016, 53(4): 599-609. Doi:10.2514/1.A33447 |
| [15] |
刘俊丽, 高扬. 十年一剑刃锋利, 苦寒方得梅花香: 全国空间轨道设计竞赛发展历程回顾[J]. 力学与实践, 2019, 41(4): 488-497. Doi:10.6052/1000-0879-19-283 |
| [16] |
张海洋. 面对快速响应任务的星下点轨迹机动优化问题研究[D]. 哈尔滨: 哈尔滨工业大学, 2019.
|
| [17] |
刘林. 航天器轨道理论[M]. 北京: 国防工业出版社, 2000.
|
 2024, Vol. 41
2024, Vol. 41 


