2. 广西大学机械工程学院, 南宁 530004;
3. 华中科技大学数字制造装备与技术国家重点实验室, 武汉 430074;
4. 江苏万基传动科技有限公司, 江苏 泰州 225400
2. School of Mechanical Engineering, Guangxi University, Nanning 530004, China;
3. State Key Lab of Digital Manufacturing Equipment and Technology, Huazhong University of Science and Technology, Wuhan 430074, China;
4. Jiangsu Wanji Transmission Technology Co., Ltd., Taizhou 225400, Jiangsu, China
时变啮合刚度作为齿轮传动系统产生振动的主要因素,是动力学研究中的重要环节。因此,精确地计算齿轮副时变啮合刚度是一项重中之重的工作。齿轮时变啮合刚度的计算方法主要有材料力学法、弹性力学法、石川公式法和有限元法等。文献[1]根据势能法对直齿轮的时变啮合刚度进行计算。文献[2]提出切片法来计算直齿轮时变啮合刚度,并研究裂纹对时变啮合刚度的影响。文献[3]提出理想状态下的直齿轮、斜齿轮时变啮合刚度方程。文献[4-5]利用有限元法对面齿轮啮合刚度进行计算。文献[6]提出运用累积积分能量法计算斜齿轮的时变啮合刚度,并分析模数、齿数、齿宽等因素对时变啮合刚度的影响。文献[7-8]在不计齿面摩擦的理想状态下,对基圆与齿根圆不重合的情况下的累积积分能量法进行修正计算。
计及齿面摩擦情况,文献[9-11]建立了计及摩擦的直齿轮啮合刚度模型,研究定摩擦因数对直齿轮时变啮合刚度的影响规律,同时分析不同载荷和转矩对时变啮合刚度的影响;文献[12]研究齿面摩擦学和动力学之间的耦合关系;文献[13]进行弧齿轮齿面摩擦的计算;文献[14]考虑了齿尖圆角和摩擦对直齿轮刚度的影响;文献[15]基于势能法建立含摩擦的斜齿轮时变啮合刚度模型,研究摩擦和啮合不对中对时变啮合刚度的影响。
综上所述,目前同时考虑定摩擦和时变摩擦对斜齿轮时变啮合刚度影响的研究鲜见报道。因此,本文以势能法、切片法为基础,计及齿面摩擦力的影响,建立含时变摩擦的斜齿轮副时变啮合刚度模型,探讨定摩擦以及不同的齿面粗糙度、转矩、转速、齿宽等因素对含有时变摩擦的斜齿轮副时变啮合刚度的影响。
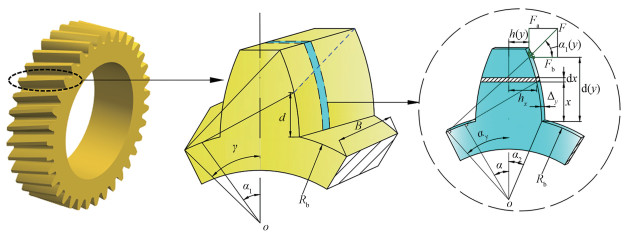
1 斜齿轮副啮合刚度切片计算模型直齿轮齿廓沿着整个齿面宽度同时进入和退出接触面,接触线长度相当于齿宽,所以计算直齿轮时变啮合刚度时,直接运用能量法计算。然而,斜齿轮在啮合时,接触线长度从零逐渐变为最大,然后从最大逐渐变为零,使得斜齿轮的特性不同于直齿轮,斜齿轮刚度的算法不同于直齿轮刚度算法。因此,计算斜齿轮时变啮合刚度时应该先进行微分切片分割计算,再根据微元切片模型积分计算整体时变啮合刚度,图 1为斜齿轮的切片模型。
|
Download:
|
| 图 1 斜齿轮切片模型 Fig. 1 The slicing model of helical gear | |
计算直齿轮时变啮合刚度时,一般采用能量法进行时变啮合刚度计算,能量法公式如下
| $ \left\{U_{\mathrm{h}}=\frac{F^2}{2 k_{\mathrm{h}}}, U_{\mathrm{b}}=\frac{F^2}{2 k_{\mathrm{b}}}, U_{\mathrm{s}}=\frac{F^2}{2 k_{\mathrm{s}}}, U_{\mathrm{a}}=\frac{F^2}{2 k_{\mathrm{a}}} .\right. $ | (1) |
其中:Uh、Ub、Us和Ua分别为储存在轮齿的赫兹接触、弯曲、剪切和轴向压缩势能,F是沿啮合线方向的啮合力。
根据累积积分势能法可知,斜齿轮弯曲、剪切、压缩刚度公式如下
| $ k_{\mathrm{b}}=\sum\limits_{i=1}^{N} \frac{\Delta y}{\int_{-\alpha_{y}^{\prime}}^{\alpha_{2}} \frac{3\left(1+k_{1}\right)^{2}\left(\alpha_{2}-\alpha\right)}{2 E A^{3}} \mathrm{~d} \alpha} , $ | (2) |
| $ k_{\mathrm{s}}=\sum\limits_{i=1}^{N} \frac{\Delta y}{\int_{-\alpha_{y}^{\prime}}^{\alpha_{2}} \frac{1.2(1+v) k_{2} \cos ^{2} \alpha_{y}^{\prime}}{E A} \mathrm{~d} \alpha} , $ | (3) |
| $ k_{\mathrm{a}}=\sum\limits_{i=1}^{N} \frac{\Delta y}{\int_{-\alpha_{y}^{\prime}}^{\alpha_{2}} \frac{k_{2} \sin ^{2} \alpha_{y}^{\prime}}{2 E A} \mathrm{~d} \alpha} . $ | (4) |
式(2) 式(4) 中:
赫兹接触刚度沿作用线是恒定不变的,与齿轮的啮合过程无关。所以,根据赫兹接触定律,赫兹接触刚度公式如下
| $ k_{\mathrm{h}}=\pi E B / 4\left(1-v^{2}\right) . $ | (5) |
根据文献[14]可知基体刚度公式如下
| $ k_{\mathrm{f}}=\frac{E \Delta y\left[\frac{L^{*} u_{\mathrm{f}}^{2}}{s_{\mathrm{f}}^{2}}+\frac{M^{*} u_{\mathrm{f}}}{s_{\mathrm{f}}}+P^{*}+P^{*} Q^{*} \tan ^{2} \alpha_{y}^{\prime}\right]}{\cos ^{2} \alpha_{y}^{\prime}} . $ | (6) |
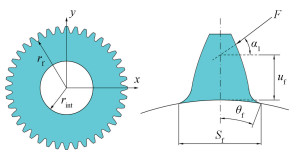
系数L*, M*, P*, Q*可以用下式进行多项式函数逼近,对应的各个参数取值参考文献[16]和图 2。
| $ X_{i}^{*}=A_{i} / \theta_{\mathrm{f}}^{2}+B_{i} h_{\mathrm{fi}}^{2}+C_{i} h_{\mathrm{f} i} / \theta_{\mathrm{f}}+E_{i} h_{\mathrm{fi}}+F_{i}. $ | (7) |
|
Download:
|
| 图 2 轮齿基体几何参数 Fig. 2 Geometric parameters of gear tooth base | |
综上所述,斜齿轮的单齿刚度公式如下
| $ k_{\mathrm{d}}=\frac{1}{k_{\mathrm{f} 1}}+\frac{1}{k_{\mathrm{b} 1}}+\frac{1}{k_{\mathrm{s} 1}}+\frac{1}{k_{\mathrm{a} 1}}+\frac{1}{k_{\mathrm{f} 2}}+\frac{1}{k_{\mathrm{b} 2}}+\frac{1}{k_{\mathrm{s} 2}}+\frac{1}{k_{\mathrm{a} 2}}+\frac{1}{k_{\mathrm{h}}}. $ | (8) |
n对齿轮副的综合刚度公式如下
| $ \left\{\begin{array}{l} k_{1, i}=\frac{1}{k_{\mathrm{f} 1, i}}+\frac{1}{k_{\mathrm{b} 1, i}}+\frac{1}{k_{\mathrm{s} 1, i}}+\frac{1}{k_{\mathrm{a} 1, i}}, \\ k_{2, i}=\frac{1}{k_{\mathrm{f} 2, i}}+\frac{1}{k_{\mathrm{b} 2, i}}+\frac{1}{k_{\mathrm{s} 2, i}}+\frac{1}{k_{\mathrm{a} 2, i}}, \\ k_{t}=\frac{1}{k_{1, i}+k_{2, i}+1 / k_{\mathrm{h}}}. \end{array}\right. $ | (9) |
式(8)、式(9)中:下标1、2分别表示主动轮、从动轮;i表示啮合齿轮的对数。
2.2 斜齿轮副时变摩擦因数计算根据Xu等[17]提出的基于粗糙表面热弹流润滑模型获得的时变摩擦因数μ的计算公式如下
| $ \mu=\mathrm{e}^{f\left(S R_{k}, P_{h K}, v_{0}, R_{a}\right)} P_{h K}^{b_{2}}\left|S R_{k}\right|^{b_{3}} V_{e k}^{b_{6}} v_{0}^{b_{7}} R_{k}^{b_{8}} , $ | (10) |
| $ \left\{\begin{array}{l} f=b_{1}+b_{4}\left|S R_{k}\right| P_{h K} \lg v_{0}+b_{5} \mathrm{e}^{S}+b_{9} \mathrm{e}^{R_{a}} , \\ S=-\left|S R_{k}\right| P_{h K} \lg v_{0} . \end{array}\right. $ | (11) |
其中:VsK为相对滑动速度,VeK为卷吸速度,SRk为滑滚比,RK为综合曲率半径,PhK为齿轮接触应力;v0为绝对黏度,bi(i=1~9)为回归系数详见文献[18]。表 1给出斜齿轮副的一些基础参数。
|
|
表 1 斜齿轮副基础参数 Table 1 Basic parameters of helical gears |
齿轮在啮合过程中,参与啮合的齿对数与齿轮的重合度有关。因为斜齿轮的重合度2 < ε < 3,啮合齿对总是在2~3对齿。因此,在一个周期内每一对齿轮上的时变摩擦因数的变化是相同的。
根据实际工况选取齿面粗糙度为0.4、0.8、1.2和1.6 μm,转矩为500、1 000、1 500和2 000 N ·m,转速为500、1 000、1 500和2 000 r/min,齿宽的区间为25、30、35和40 mm。图 3(a)~3(d)分别给出不同区间的齿面粗糙度、转矩、转速、齿宽等因素对齿轮时变摩擦因数的影响。

|
Download:
|
| 图 3 不同因素下的时变摩擦因数变化规律 Fig. 3 Variation law of time-varying friction coefficient under different factors | |
由图 3(a)~3(d)可知,随着啮合时间的推移,时变摩擦因数呈现先减小后增大,且啮合到节线位置变为0的规律。同时,时变摩擦因数会分别随着齿面粗糙度、转矩、齿宽的增大而增大,其中齿面粗糙度的影响最大,但会随着转速增大而减小。
2.3 含齿面摩擦的斜齿轮副时变啮合刚度斜齿轮进行微元切片之后,每一片微元齿轮可以近似看成是直齿轮。齿轮在微元切片后并不会改变齿面摩擦力的方向,齿面摩擦力的方向只与齿轮的啮合位置有关系。当齿轮的啮合位置在节线下面时,处于啮入阶段,摩擦力方向背离节线方向;当啮合位置在节线上面,处于啮出阶段,摩擦力背离节线方向;当齿轮啮合线与节线相重合的位置时,摩擦力为0,且齿轮啮合接触点处的相对滑动速度的方向将会在此位置发生反向,从而导致齿面间的摩擦力的方向发生变化。
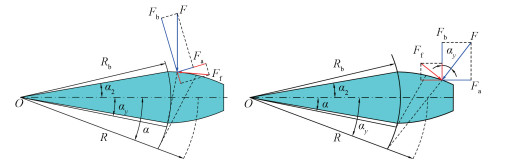
齿轮在啮入和啮出阶段的受力分析如图 4所示,其中F代表齿轮啮合时的啮合力,Fa和Fb分别表示其水平和竖直方向分力,Ff表示齿轮副间的齿面摩擦力。
|
Download:
|
| 图 4 啮入与啮出阶段受力分析 Fig. 4 Force analysis of meshing in and out stages | |
摩擦力的计算及分解公式如下
| $ \left\{\begin{array}{l} F_{\mathrm{f}}=\mu F, \\ F_{\mathrm{f} 1}=F_{\mathrm{f}} \cos \alpha_{y}, \\ F_{\mathrm{f} 2}=F_{\mathrm{f}} \sin \alpha_{y} . \end{array}\right. $ | (12) |
将摩擦力分解之后加入到各部分时变啮合刚度的表达式中,并且计算方法与累积积分势能法[6]相同。含有摩擦的弯曲刚度、剪切刚度和压缩刚度公式如下
| $ k_{\mathrm{b}}=\left\{\begin{array}{l} \sum\limits_{i=1}^N \frac{\Delta y}{\int_{-\alpha_y^{\prime}}^{\alpha_2} \frac{3\left\{1+f(\alpha)-M_b\right\}^2\left(\alpha_2-\alpha\right)}{2 E A^3} \mathrm{~d} \alpha}, \\ \sum\limits_{i=1}^N \frac{\Delta y}{\int_{-\alpha_y^{\prime}}^{\alpha_2} \frac{3\left\{1+f(\alpha)+M_b\right\}^2\left(\alpha_2-\alpha\right)}{2 E A^3} \mathrm{~d} \alpha} . \end{array} \right. $ | (13) |
| $ k_{\mathrm{s}}=\left\{\begin{array}{l} \sum\limits_{i=1}^N \frac{\Delta y}{\int_{-\alpha_y^{\prime}}^{\alpha_2} \frac{1.2(1+v) k_2\left(\cos \alpha_y^{\prime}-M_s\right)^2}{E A} \mathrm{~d} \alpha}, \\ \sum\limits_{i=1}^N \frac{\Delta y}{\int_{-\alpha_y^{\prime}}^{\alpha_2} \frac{1.2(1+v) k_2\left(\cos \alpha_y^{\prime}+M_s\right)^2}{E A} \mathrm{~d} \alpha} . \end{array}\right. $ | (14) |
| $ \begin{align*} & k_{\mathrm{a}}=\left\{\begin{array}{l} \sum\limits_{i=1}^{N} \frac{\Delta y}{\int_{-\alpha_{y}^{\prime}}^{\alpha_{2}} \frac{\left(\alpha_{2}-\alpha\right) \cos \alpha\left(\sin \alpha_{y}^{\prime}+M_{a}\right)^{2}}{2 E A}} \mathrm{~d} \alpha \\ \sum\limits_{i=1}^{N} \frac{\Delta y}{\int_{-\alpha_{y}^{\prime}}^{\alpha_{2}} \frac{\left(\alpha_{2}-\alpha\right) \cos \alpha\left(\sin \alpha_{y}^{\prime}-M_{a}\right)^{2}}{2 E A} \mathrm{~d} \alpha} . \end{array}\right. \end{align*} $ | (15) |
式(13) 式(15) 中,
|
Download:
|
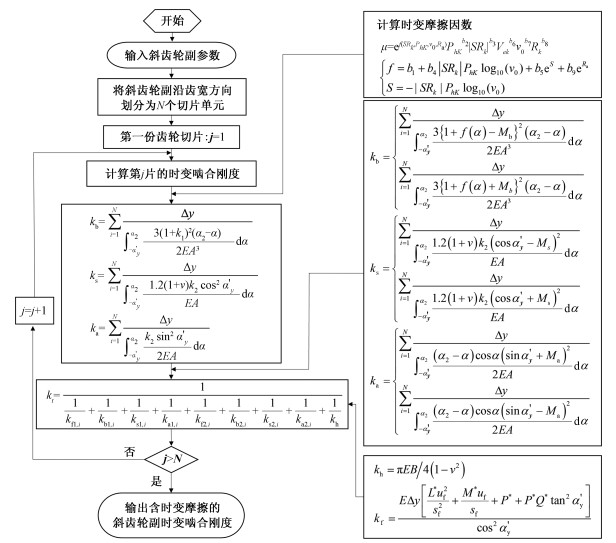
| 图 5 斜齿轮摩擦时变啮合刚度计算流程图 Fig. 5 Calculation procedure for friction TVMS of helical gear | |
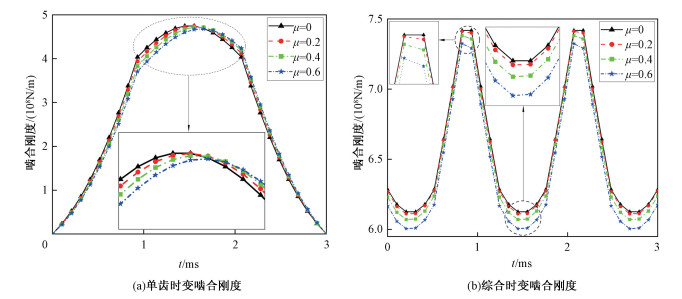
齿轮啮合时,摩擦力的存在使得齿轮的单齿刚度在啮入和啮出阶段发生改变;节线处摩擦力的大小为0,方向发生突变,斜齿轮副啮合刚度在节线处发生突变;不同的定摩擦因数下的斜齿轮时变啮合刚度的变化规律如图 6(a)~6(b)所示。分析可知,在定摩擦因数的作用下斜齿轮时变啮合刚度有所改变,单齿刚度在啮入阶段减小,啮出阶段增大,综合时变刚度总体减小。而且定摩擦因数越大,啮合刚度变化量越大。
|
Download:
|
| 图 6 斜齿轮时变啮合刚度 Fig. 6 TVMS of helical gear | |
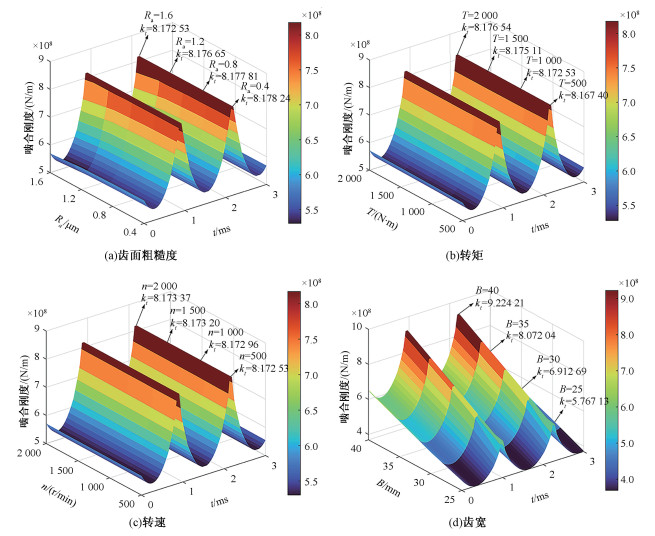
在时变摩擦力的作用下,由于时变摩擦因数变化产生的影响,使得斜齿轮的综合时变啮合刚度整体会发生变化,总体上会比正常时变啮合刚度小。在不同的时变摩擦因数下,时变啮合刚度的变化规律并不相同,图 7(a)~7(d)给出了考虑不同时变摩擦因数下斜齿轮副综合刚度变化规律。分析可知,在考虑单一变量的条件下,齿面粗糙度、转矩、转速和齿宽对时变啮合刚度的影响各不相同。时变啮合刚度随着齿面粗糙度的增大,逐渐减小;但会分别随着转矩、转速、齿宽的增大而逐渐增大,且受齿宽的影响最为明显。
|
Download:
|
| 图 7 不同因素下的时变啮合刚度变化规律 Fig. 7 Variation law of TVMS under different factors | |
传递误差是描述齿轮传动不平稳的参数,衡量齿轮啮合是否偏离啮合线,其计算公式如下
| $ \text { LSTE }=F / K . $ | (16) |
其中:F是啮合力,K是时变啮合刚度。
同时,传递误差和时变啮合刚度是相互影响耦合的,所以当时变啮合刚度随着时变摩擦因数变化时,传递误差也会随着其变化。
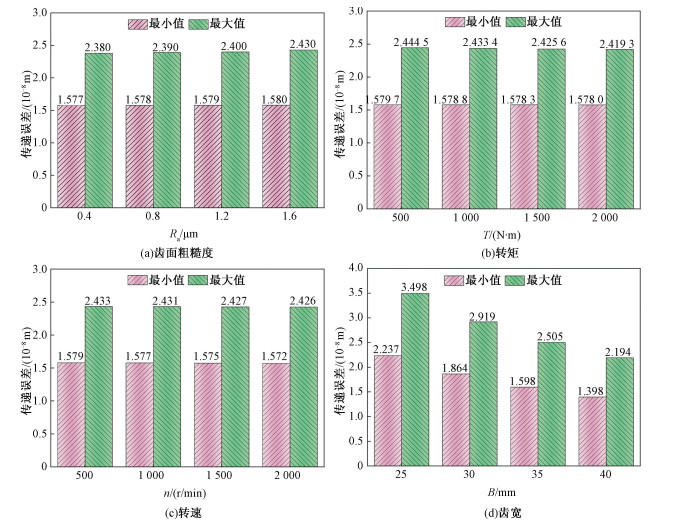
图 8(a)~8(d)给出了不同时变摩擦因数下斜齿轮副的传递误差变化规律。分析可知,在考虑单一变量的条件下,齿面粗糙度、转矩、转速和齿宽对传递误差的影响各不相同。传递误差随着齿面粗糙度的增大逐渐增大;但会随着转矩、转速、齿宽的增大而逐渐减小,且受齿宽的影响最为明显。
|
Download:
|
| 图 8 不同因素下的传递误差变化规律 Fig. 8 Variation law of LSTE under different factors | |
1) 针对本文给定的齿轮模型,将斜齿轮简化为齿根圆上的悬臂梁结构,计及齿面摩擦,建立时变摩擦因数计算模型,基于切片法和势能法将其代入到时变啮合刚度公式中,从而提出一种考虑时变摩擦的斜齿轮副时变啮合刚度算法。
2) 分析齿面粗糙度、转矩、转速以及齿宽对时变摩擦因数的影响。时变摩擦因数会分别随着齿面粗糙度、输入转矩和齿宽的增大而增大;但随着转速的增大而减小。
3) 分析齿面粗糙度、转矩、转速以及齿宽对时变啮合刚度的影响。时变啮合刚度会随着齿面粗糙度的增大而逐渐减小;但分别随着输入转矩、转速和齿宽的增大而逐渐增大。
| [1] |
马辉, 逄旭, 宋溶泽, 等. 基于改进能量法的直齿轮时变啮合刚度计算[J]. 东北大学学报(自然科学版), 2014, 35(6): 863-866, 884. Doi:10.3969/j.issn.1005-3026.2014.06.023 |
| [2] |
Chen Z G, Shao Y M. Dynamic simulation of spur gear with tooth root crack propagating along tooth width and crack depth[J]. Engineering Failure Analysis, 2011, 18(8): 2149-2164. Doi:10.1016/j.engfailanal.2011.07.006 |
| [3] |
Gu X, Velex P, Sainsot P, et al. Analytical investigations on the mesh stiffness function of solid spur and helical gears[J]. Journal of Mechanical Design, 2015, 137(6): 063301. Doi:10.1115/1.4030272 |
| [4] |
莫帅, 岳宗享, 冯志友, 等. 面齿轮分汇流系统动力学均载特性研究[J]. 华中科技大学学报(自然科学版), 2020, 48(2): 23-28. Doi:10.13245/j.hust.200205 |
| [5] |
Mo S, Zhang T, Jin G G, et al. Analytical investigation on load sharing characteristics of herringbone planetary gear train with flexible support and floating sun gear[J]. Mechanism and Machine Theory, 2020, 144: 103670. Doi:10.1016/j.mechmachtheory.2019.103670 |
| [6] |
Wan Z G, Cao H R, Zi Y Y, et al. Mesh stiffness calculation using an accumulated integral potential energy method and dynamic analysis of helical gears[J]. Mechanism and Machine Theory, 2015, 92: 447-463. Doi:10.1016/j.mechmachtheory.2015.06.011 |
| [7] |
刘文, 李锐, 张晋红, 等. 斜齿轮时变啮合刚度算法修正及影响因素研究[J]. 湖南大学学报(自然科学版), 2018, 45(2): 1-10. Doi:10.16339/j.cnki.hdxbzkb.2018.02.01 |
| [8] |
林腾蛟, 赵子瑞, 江飞洋, 等. 考虑温度效应的斜齿轮时变啮合刚度解析算法[J]. 湖南大学学报(自然科学版), 2020, 47(2): 6-13. Doi:10.16339/j.cnki.hdxbzkb.2020.02.002 |
| [9] |
Saxena A, Parey A, Chouksey M. Time varying mesh stiffness calculation of spur gear pair considering sliding friction and spalling defects[J]. Engineering Failure Analysis, 2016, 70: 200-211. Doi:10.1016/j.engfailanal.2016.09.003 |
| [10] |
黄康, 汪涛, 熊杨寿, 等. 计及摩擦影响的直齿轮时变啮合刚度计算方法[J]. 应用力学学报, 2017, 34(3): 564-569. Doi:10.11776/cjam.34.03.B046 |
| [11] |
杨勇, 王家序, 周青华, 等. 考虑摩擦的磨损和修形齿轮啮合刚度计算[J]. 工程科学与技术, 2018, 50(2): 212-219. Doi:10.15961/j.jsuese.201700574 |
| [12] |
邹玉静, 庞峰, 樊智敏. 渐开线斜齿轮传动摩擦动力学耦合研究[J]. 机械工程学报, 2019, 55(3): 109-119. Doi:10.3901/JME.2019.03.109 |
| [13] |
李飞, 袁茹, 朱慧玲, 等. 计及齿面摩擦的弧齿锥齿轮动态特性[J]. 航空动力学报, 2020, 35(8): 1687-1694. Doi:10.13224/j.cnki.jasp.2020.08.013 |
| [14] |
Ma H, Feng M J, Li Z W, et al. Time-varying mesh characteristics of a spur gear pair considering the tip-fillet and friction[J]. Meccanica, 2017, 52(7): 1695-1709. Doi:10.1007/s11012-016-0502-3 |
| [15] |
Han L, Xu L X, Qi H J. Influences of friction and mesh misalignment on time-varying mesh stiffness of helical gears[J]. Journal of Mechanical Science and Technology, 2017, 31(7): 3121-3130. Doi:10.1007/s12206-017-0602-6 |
| [16] |
Sainsot and P, Velex P, Duverger O. Contribution of gear body to tooth deflections: a new bidimensional analytical formula[J]. Journal of Mechanical Design, 2004, 126(4): 748-752. Doi:10.1115/1.1758252 |
| [17] |
Xu H, Kahraman A, Anderson N E, et al. Prediction of mechanical efficiency of parallel-axis gear pairs[J]. Journal of Mechanical Design, 2007, 129(1): 58-68. Doi:10.1115/1.2359478 |
| [18] |
熊杨寿, 韩广志, 黄康, 等. 考虑时变摩擦系数的微线段齿轮系统动态特性分析[J]. 机械工程学报, 2021, 57(19): 113-127. Doi:10.3901/JME.2021.19.113 |
 2024, Vol. 41
2024, Vol. 41 


