2. 中国科学院大学, 北京 100049;
3. 上海科技大学, 上海 201210
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. ShanghaiTech University, Shanghai 201210, China
近年来在宽带互联网技术的推动下,宽带低轨卫星星座得到了国内外研究者的广泛关注,以OneWeb、SpaceX、Leosat等为代表的低轨卫星通信公司应运而生。得益于卫星轨道高度低、传输时延短、路径损耗小、频率复用效率高等特点[1],低轨(low earth orbit,LEO)卫星系统被认为是最具有发展潜力的卫星通信系统。目前轨道资源和频率资源日趋饱和,越来越多的LEO卫星和对地静止卫星轨道(geostationary satellite orbit,GSO)卫星共同工作在Ku、Ka等通信频段内。各个系统在频谱使用上的高度重合将导致LEO卫星对GSO地面站产生严重的同频干扰[2],如何规避LEO卫星对GSO地面站的干扰是当前低轨卫星系统亟待解决的问题。
目前,国内外针对低轨卫星通信系统中存在的干扰问题大多采用功率控制、空间隔离和认知无线电技术等方法。文献[3-4]根据LEO卫星、GSO卫星和GSO地面站的空间位置进行建模,采用功率控制的方法来抑制干扰;文献[5]通过划分不同信道以频谱复用的方式来规避系统间的干扰;文献[6]通过认知无线电的方式进行频谱复用,实现干扰规避;文献[7]在国际电信联盟(International Telecommunication Union,ITU)提出的GSO地面站隔离角和干扰规避区的概念[8-10]上引入GSO带的概念,给出了干扰规避区的确定方法。在上述策略中,功率控制会影响系统容量;划分信道将导致频谱资源利用率降低;空间隔离要权衡干扰规避效果和LEO卫星波束的有效覆盖范围,过大的隔离角将导致波束有效覆盖范围减少;随着星座规模的增大,认知无线电技术实时检测的复杂性将显著增加。
本文针对宽带低轨卫星通信系统的共线干扰场景,提出一种基于发射波束旁瓣零陷的干扰规避策略。通过建立LEO卫星坐标系求解共线区域对应的角度,并定义共线区域为干扰抑制带;将二维面阵按行、列维度划分,在列维度实现宽零陷然后在行维度进行扩展,形成一条覆盖干扰抑制带的“零陷带”。通过仿真对比,该算法较目前常采用的空间隔离策略和发射波束低旁瓣算法有更好的抗干扰性能,同时能够有效减少LEO卫星的干扰规避隔离区。
1 系统场景模型 1.1 LEO与GSO系统干扰场景图 1为GSO卫星、LEO卫星和GSO地面站的空间分布,以此模型来描述干扰场景。LEO卫星普遍采用相控阵天线实现波束覆盖,其主瓣指向LEO地面终端的同时旁瓣将不可避免地指向GSO地面站,旁瓣电平的大小将直接影响GSO地面站的通信质量。定义GSO卫星和LEO卫星的连线与地面的交点为共线点,遍历GSO弧段得到所有共线点组成的区域为共线区域。LEO卫星始终会在共线区域产生最强的干扰[11],此时LEO卫星将严重影响GSO卫星的正常通信。设GSO地面站为E点,LEO卫星为L点,GSO卫星为G点,定义EL和EG的夹角为α,遍历整个GSO弧段,定义最小的夹角α为隔离角αth,即αth=min(α)。常规的空间隔离策略依据隔离角αth定义干扰隔离区[7],LEO卫星的波束主瓣只能指向干扰隔离区两侧(|α|>αth),不能为干扰隔离区内的区域提供服务。通过设置隔离角进行约束,LEO卫星波束只有远旁瓣会指向GSO地面站,对其造成的干扰可以忽略,但将大大损失LEO卫星波束的有效覆盖范围。
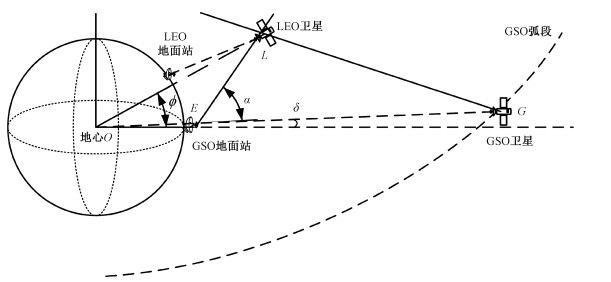
|
Download:
|
| 图 1 LEO卫星、GSO卫星和GSO地面站空间分布 Fig. 1 Spatial distribution of LEO satellite, GSO satellite and GSO ground station | |
根据国际电信联盟发布的《无线电规则》[12]条款22,宽带低轨卫星系统设计时要在Ku、Ka等频段为GSO卫星提供必要的干扰保护,需要对GSO系统接收端的等效功率通量密度(equivalent power flux density,EPFD)设定限值。EPFD定义为GSO系统接收端接收到的由NGSO系统内所有发送端产生的功率通量密度总和,其计算公式为
| $ \text { EPFD }=10 \lg \left(\sum\limits_{i=1}^N 10^{\frac{P_i}{10}} \cdot \frac{G_t\left(\theta_i\right)}{4 {\rm{\mathsf{π}}} d_i^2} \cdot \frac{G_r\left(\varphi_i\right)}{G_{r, \max }}\right), $ | (1) |
式中:N为GSO接收端可见的NGSO系统内发送端的个数;i为NGSO系统内第i个发送端;Pi为NGSO系统内第i个发送端功率;Gt(θi)为NGSO系统内第i个发送端天线离轴角为θi的增益;di为NGSO系统内第i个发送端到GSO系统接收端之间的距离;φi为NGSO系统内第i个发送端所对应的GSO系统接收端的离轴角,其增益为Gr(φi);Gr, max为GSO系统接收端的最大天线增益。
本文以LEO卫星星下点纬度为0°时的共线场景为例进行分析,如图 2所示。当LEO卫星波束主瓣指向干扰隔离区外时,其旁瓣将不可避免地落在干扰隔离区内且对共线区域造成的干扰最强,表现在波束覆盖区内是共线点附近一条很窄的“带”,条带中较大的天线增益将导致GSO地面站接收到的EPFD值超过ITU规定的门限值,本文定义这条“带”为干扰抑制带。
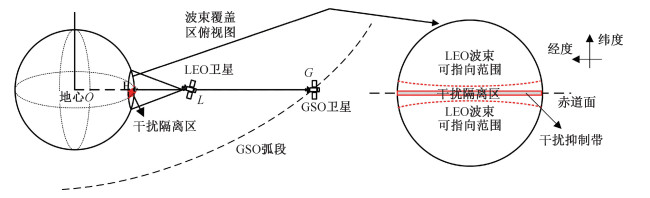
|
Download:
|
| 图 2 干扰最强几何场景示意图(0纬度) Fig. 2 Schematic diagram of geometric scene with the strongest interference (latitude=0) | |
共线干扰是低轨卫星系统中最严重的干扰问题,单一地采用空间隔离策略规避共线干扰,隔离角的增大将导致LEO卫星波束的有效覆盖范围迅速减少。当隔离角不改变时,降低共线干扰最直接的方式是降低波束的旁瓣电平。目前工程中主要采用Tapering算法[13]降低旁瓣电平,但旁瓣降低的同时也会造成主瓣增益下降、波束宽度展宽等性能损失。事实上无需牺牲主瓣增益去换取整个旁瓣的低增益,只需要波束旁瓣在共线区域有足够低的增益即可。基于这一思想,本文考虑在空间隔离的基础上结合旁瓣零陷算法在共线区域上形成一条“零陷带”来规避干扰。
2.1 LEO卫星俯仰角和方位角定义图 3为ITU-R S.1503文档[14]定义的LEO卫星坐标系。定义从LEO卫星指向东的方向为X轴,指向地心的方向为Y轴,指向北的方向为Z轴。天线单元均匀分布在XOZ面,定义俯仰角θ为空间信号与XOY面的夹角,方位角φ为空间信号在XOY面的投影与Y轴的夹角,dx、dz分别为X、Z方向上相邻阵元的间距。
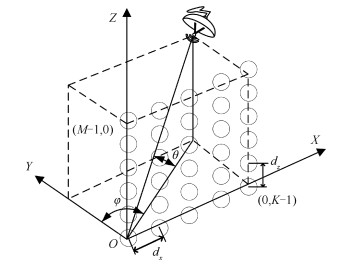
|
Download:
|
| 图 3 LEO卫星坐标系 Fig. 3 LEO satellite coordinate system | |
当GSO卫星、LEO卫星和GSO地面站三点共线时,可由GSO卫星指向LEO卫星的共线向量求得共线点相对于LEO卫星的俯仰角和方位角。如图 1所示,在地球坐标系中地心到GSO卫星的向量vOG,地心到LEO卫星的向量vOL可以分别表示为
| $ \boldsymbol{v}_{\mathrm{OG}}=\left(R_{\mathrm{g}} \sin \delta, R_{\mathrm{g}} \cos \delta, 0\right), $ | (2) |
| $ \boldsymbol{v}_{\text {OL }}=\left(0, R_1 \cos \phi, R_1 \sin \phi\right) \text {, } $ | (3) |
式中:Rg为GSO卫星到地心的距离,Rl为LEO卫星到地心的距离,ϕ为LEO卫星星下点纬度,δ为GSO卫星的相对经度差。当GSO卫星、LEO卫星与GSO地面站共线时,定义从GSO卫星指向LEO卫星的向量为共线向量vGL,l为vGL的单位向量:
| $ \boldsymbol{l}=\frac{\boldsymbol{v}_{\mathrm{OL}}-\boldsymbol{v}_{\mathrm{OG}}}{\left|\boldsymbol{v}_{\mathrm{OL}}-\boldsymbol{v}_{\mathrm{OG}}\right|} . $ | (4) |
在地球坐标系中,前述LEO卫星坐标系的Y轴单位向量可表示为y′=(0, -cosϕ, -sinϕ),Z轴单位向量可表示为z′=(0, -sinϕ, cosϕ)。根据图 3中对俯仰角和方位角的定义,可分别由式(5)和式(6)求得共线点对应的俯仰角θi和方位角φi:
| $ \theta_i=\frac{{\rm{\mathsf{π}}}}{2}-\arccos \left(\frac{\boldsymbol{l} \cdot \boldsymbol{z}^{\prime}}{|\boldsymbol{l}|\left|\boldsymbol{z}^{\prime}\right|}\right), $ | (5) |
| $ \varphi_i=\arccos \left(\frac{\boldsymbol{m} \cdot \boldsymbol{y}^{\prime}}{|\boldsymbol{m}|\left|\boldsymbol{y}^{\prime}\right|}\right), $ | (6) |
式中,m为l在XOZ面的投影向量,可以表示为
| $ \boldsymbol{m}=\boldsymbol{l}-|\boldsymbol{l}| \cdot \cos \left(\frac{{\rm{\mathsf{π}}}}{2}-\theta_i\right) . $ | (7) |
改变GSO卫星的相对经度差δ,遍历整个GSO弧段可以求得LEO卫星覆盖范围内所有共线点对应的俯仰角和方位角。本文取Rg为42 143 km,Rl为7 407 km,GSO卫星相对经度差δ取值为-55°~55°,步长1°。在本文所述场景下,当LEO卫星星下点纬度ϕ为0°时,可求得所有共线点对应的角度分布,如图 4所示。

|
Download:
|
| 图 4 共线区域仿真图 Fig. 4 Simulation diagram of collinear area | |
从图 4可以看出,当LEO卫星星下点纬度为0°时,遍历GSO弧段得到的共线点区域是一条直线,此处共线点组成的区域即为上文定义的干扰抑制带,要求在此区域内波束的旁瓣电平足够低来降低EPFD。
2.3 阵列模型与权值系数求解假设天线阵列采用
| $ \left\{\begin{array}{l} Z \text { 轴: } \frac{2 {\rm{\mathsf{π}}}}{\lambda} m d \sin \theta, m=0, 1, \cdots, M-1, \\ X \text { 轴: } \frac{2 {\rm{\mathsf{π}}}}{\lambda} k d \cos \theta \sin \varphi, k=0, 1, \cdots K-1 . \end{array}\right. $ | (8) |
从而,在列阵元(Z轴方向)和行阵元(X轴方向)2个维度的导向矢量az和ax可以分别表示为
| $ \begin{gathered} \boldsymbol{a}_z(\theta)=\left[1, \mathrm{e}^{\mathrm{j} 2 {\rm{\mathsf{π}}} d \sin \theta / \lambda}, \cdots, \mathrm{e}^{\mathrm{j} 2 {\rm{\mathsf{π}}}(M-1) d \sin \theta / \lambda}\right]^{\mathrm{T}}, \\ \boldsymbol{a}_x(\theta, \varphi)=\left[1, \mathrm{e}^{\mathrm{j} 2 {\rm{\mathsf{π}}} d \cos \theta \sin \varphi / \lambda}, \cdots, \mathrm{e}^{\mathrm{j} 2 {\rm{\mathsf{π}}}(K-1) d \cos \theta \sin \varphi / \lambda}\right]^{\mathrm{T}} . \end{gathered} $ | (10) |
记阵元的幅值系数为amk,当阵元幅值均匀分布(amk=1)时,忽略单个天线单元方向图的影响,整个面阵的发射波束方向图可以表示为
| $ \begin{aligned} F(\theta, \varphi) & =\sum\limits_{m=0}^{M-1} \sum\limits_{k=0}^{K-1} a_{m k} \mathrm{e}^{\mathrm{j} \frac{2 {\rm{\mathsf{π}}} d}{\lambda}\left[m\left(\sin \theta-\sin \theta_0\right)+k\left(\cos \theta \sin \varphi-\cos \theta_0 \sin \varphi_0\right)\right]} \\ & =\sum\limits_{m=0}^{M-1} \mathrm{e}^{\mathrm{j} \frac{2 {\rm{\mathsf{π}}} m d}{\lambda}\left(\sin \theta-\sin \theta_0\right)} \sum\limits_{n=0}^{K-1} \mathrm{e}^{\mathrm{j} \frac{2 {\rm{\mathsf{π}}} k d}{\lambda}\left(\cos \theta \sin \varphi-\cos \theta_0 \sin \varphi_0\right)} \\ & =F_1(\theta) F_2(\theta, \varphi) . \end{aligned} $ | (11) |
式中,θ0, φ0为波束的空间指向。由此可得,整个面阵的发射波束方向图可以表示为列、行维度上2个线阵方向图F1(θ)与F2(θ, φ)的乘积,其中F1(θ)为列维度的线阵方向图,仅包含俯仰角信息。
在列阵元维度将方阵视为K个完全相同的M元均匀线阵,任取一列阵元,设其每个阵元发送的信号为s0(t),发送角度为θ0,对应的导向矢量为az(θ0),则阵列的发送信号可以表示为
| $ \boldsymbol{x}(t)=s_0(t) \boldsymbol{a}_z\left(\theta_0\right), $ | (12) |
整个线阵加权合成后的信号可以表示为
| $ y(t)=\boldsymbol{w}_z^{\mathrm{H}} \boldsymbol{x}(t)=\boldsymbol{w}_z^{\mathrm{H}} \boldsymbol{a}_z\left(\theta_0\right) s_0(t), $ | (13) |
式中:
| $ E_z(\theta)=s_0(t) \boldsymbol{w}_z^{\mathrm{H}} \boldsymbol{a}_z(\theta) . $ | (14) |
当
传统LCMV算法[15]的目标函数和约束条件为
| $ \left\{\begin{array}{l} \underset{\boldsymbol{w}}{\min } \boldsymbol{w}^{\mathrm{H}} \boldsymbol{R} \boldsymbol{w} ,\\ \text { s. t. } \boldsymbol{C}^{\mathrm{H}} \boldsymbol{w}=\boldsymbol{f}. \end{array}\right. $ | (15) |
式中:
| $ \boldsymbol{C}=\left[\boldsymbol{a}\left(\theta_0\right), \boldsymbol{a}\left(\theta_1\right), \cdots, \boldsymbol{a}\left(\theta_P\right)\right], $ | (16) |
| $ \boldsymbol{f}=[1, 0, \cdots, 0]^{\mathrm{T}} . $ | (17) |
为防止信号的协方差矩阵为奇异矩阵,对其进行对角加载处理,令
| $ \boldsymbol{R}=\boldsymbol{C} \boldsymbol{C}^{\mathrm{H}}+\sigma \boldsymbol{I}, $ | (18) |
式中:σ为一个很小的正实数,I为单位矩阵。此外,由于阵列中存在的幅度误差、相位误差、通道一致性误差以及相邻阵元之间的耦合作用产生的误差等,零陷的位置会发生不确定的随机偏移。为保证始终能在共线区域形成零陷,在共线点两侧施加额外的约束来展宽零陷,从而优化问题可以更新为
| $ \left\{\begin{array}{l} \min\limits_\boldsymbol{w} \sum\limits_{p=0}^P\left|\boldsymbol{w}_z^{\mathrm{H}} \boldsymbol{a}_z\left(\theta_p\right)\right|^2, \\ \text { s. t. } \boldsymbol{w}_z^{\mathrm{H}} \boldsymbol{a}_z\left(\theta_0\right)=1, \\ \text { s. t. } \boldsymbol{w}_z^{\mathrm{H}} \boldsymbol{a}_z\left(\theta_p\right)=0, p=1, 2, \cdots, P, \\ \text { s. t. } \boldsymbol{w}_z^{\mathrm{H}} \boldsymbol{a}_z\left(\theta_p \pm \Delta \theta\right)=0, p=1, 2, \cdots, P . \end{array}\right. $ | (19) |
式中,Δθ是共线点俯仰角附近的偏移量,取值很小。定义新的约束矩阵C′和响应矢量f′
| $ \begin{aligned} \boldsymbol{C}^{\prime}= & {\left[\boldsymbol{C}, \boldsymbol{a}\left(\theta_1-\Delta \theta\right), \cdots, \boldsymbol{a}\left(\theta_p-\Delta \theta\right), \right.} \\ & \left.\boldsymbol{a}\left(\theta_1+\Delta \theta\right), \cdots, \boldsymbol{a}\left(\theta_P+\Delta \theta\right)\right], \end{aligned} $ | (20) |
| $ \boldsymbol{f}^{\prime}=[\boldsymbol{f}, 0, \cdots, 0]^{\mathrm{T}} \text {. } $ | (21) |
通过引入拉格朗日乘子矢量对上述优化问题进行求解,可得列阵元的最优加权矢量为
| $ \boldsymbol{w}_z=\boldsymbol{R}^{-1} \boldsymbol{C}^{\prime}\left(\boldsymbol{C}^{\prime \mathrm{H}} \boldsymbol{R}^{-1} \boldsymbol{C}^{\prime}\right)^{-1} \boldsymbol{f}^{\prime} . $ | (22) |
对于所有K个列维度线阵,这组加权矢量wz均能使发射波束的主瓣指向θ0的同时在共线区域形成宽零陷。
在行阵元维度将方阵视为
| $ E_x(\theta, \varphi)=s_0(t) \boldsymbol{w}_x^{\mathrm{H}} \boldsymbol{a}_x(\theta, \varphi), $ | (23) |
式中:
| $ \boldsymbol{w}_x=\boldsymbol{a}_x\left(\theta_0, \varphi_0\right) . $ | (24) |
同样地, 对于所有
最后对于整个面阵而言,列维度阵元的加权系数根据稳健LCMV算法求得, 其幅值系数不再均匀分布, 但行维度的加权矢量为导向矢量, 每一行的阵元幅值仍均匀分布, 有
| $ \begin{aligned} F(\theta, \boldsymbol{\theta}) & =\sum\limits_{m=0}^{M-1} \sum\limits_{k=0}^{K-1} a_{m k} \mathrm{e}^{\mathrm{j} \frac{2 {\rm{\mathsf{π}}} d}{\lambda}\left[m\left(\sin \theta-\sin \theta_0\right)+k\left(\cos \theta \sin \varphi-\cos \theta_0 \sin \varphi_0\right)\right]} \\ & =\sum\limits_{m=0}^{M-1} a_{m 0} \mathrm{e}^{\mathrm{j} \frac{2 {\rm{\mathsf{π}}} m d}{\lambda}\left(\sin \theta-\sin \theta_0\right)} \sum\limits_{n=0}^{K-1} \mathrm{e}^{\mathrm{j} \frac{2 {\rm{\mathsf{π}}} k d}{\lambda}\left(\cos \theta \sin \varphi-\cos \theta_0 \sin \varphi_0\right)} \\ & =F_1^{\prime}(\theta) F_2(\theta, \varphi). \end{aligned} $ | (25) |
从而,整个面阵的加权系数矩阵W可以由行阵元和列阵元的加权系数矢量进行矩阵乘法求得
| $ \begin{aligned} \boldsymbol{W} & =\boldsymbol{w}_z \cdot \boldsymbol{w}_x^{\mathrm{T}} \\ & =\left[\begin{array}{cccc} w_{z 1} w_{x 1} & w_{z 1} w_{x 2} & \cdots & w_{z 1} w_{x K} \\ w_{z 2} w_{x 1} & w_{z 2} w_{x 2} & \cdots & w_{z 2} w_{x K} \\ \vdots & \vdots & \ddots & \vdots \\ w_{z M} w_{x 1} & w_{z M} w_{x 2} & \cdots & w_{z M} w_{x K} \end{array}\right] \end{aligned} $ | (26) |
权值矩阵W可以看作是列阵元维度的加权系数在行阵元维度上的扩展,经过这样的二维扩展后,整个面阵的波束方向图将在三维空间里表现为方位角方向上的一条“零陷带”。“零陷带”覆盖了共线区域,大幅降低了指向共线区域的波束增益。阵列加权系数矩阵的求解步骤可以总结为如图 5所示的流程图。
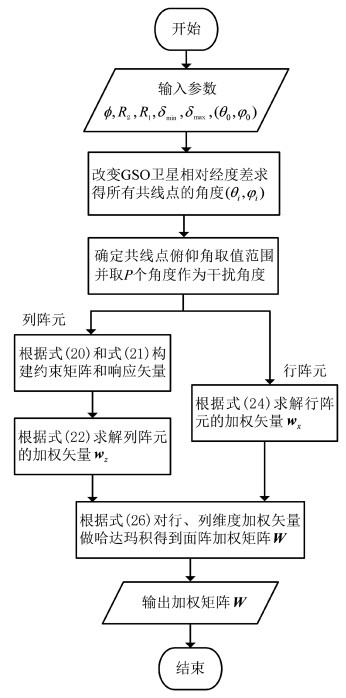
|
Download:
|
| 图 5 本文算法流程图 Fig. 5 Flow chart of the algorithm in this paper | |
本文所提基于扩展的LCMV算法通过建立LEO卫星坐标系,将整个M×K元二维面阵权值系数的求解转化为M×1元线阵权值系数的求解,以降维的方式将全阵列加权系数优化转换为对线阵加权系数的优化,算法复杂度和计算量将大幅降低。根据式(22),列阵元加权系数的求解主要涉及矩阵乘法、矩阵求逆运算,其时间复杂度为O(M3)。本文取M=16,根据图 5所示的算法流程图统计浮点运算次数,最终可得完成整个算法卫星载荷需要增加约6万次浮点运算。
当LEO卫星高速运动时,改变星下点纬度对共线区域进行仿真。通过仿真分析可知:当星下点纬度超过45°时不再有共线区域存在;当星下点纬度在0°~45°间每变化1°时,共线区域宽度的变化量最多不超过1°。而本文算法形成的宽零陷在覆盖共线区域后还有一定的余量,即当卫星运动1°以内时,前一时刻形成的零陷仍然能覆盖当下时刻的共线区域。以目前卫星载荷通常采用的TMS320C6678型号数字信号处理器为例,该处理器有8个核心,主频为1.0 GHz,单核可支持20 GFLOPS。假设波束控制部分占用载荷计算资源的10 %,根据本文所提算法计算整个面阵的加权系数用时约为3.75 μs。取LEO卫星轨道高度为1 050 km,则卫星运动1周用时约106 min,即卫星运行1°用时约为17.67 s,相比之下卫星载荷能在可接受的时间内计算下一组阵列加权系数,满足快速响应。
3 仿真结果与分析 3.1 仿真参数选取与设置通过仿真对比不采用低旁瓣算法、采用Tapering算法和采用本文所提算法的波束方向图以及3种策略下的单星下行链路EPFD仿真值,进一步论证所提策略的优势。本文主要的仿真参数见表 1。
|
|
表 1 主要仿真参数 Table 1 Main simulation parameters |
选取LEO卫星星下点纬度为0°的场景进行仿真,由前述分析可知在此场景下波束需要在俯仰角0°左右有足够低的旁瓣电平。考虑到在空间隔离策略下LEO卫星的波束主瓣指向干扰隔离区两侧,在干扰隔离区外随机取波束主瓣指向角度(θ0, φ0)为(25°, 0°),通过仿真给出不采用低旁瓣算法、采用Tapering算法和采用本文所提算法的空间三维波束方向图,如图 6所示。
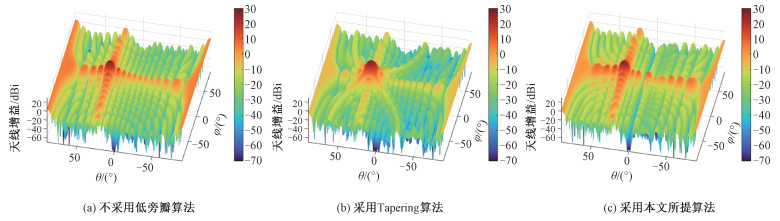
|
Download:
|
| 图 6 采用不同策略的三维波束方向图 Fig. 6 3D beam pattern using different strategies | |
图 6为采用不同策略后的发射波束三维方向图,波束主瓣均指向(25°, 0°)。图 6(a)不采用低旁瓣算法时波束旁瓣衰减缓慢,在俯仰角为0°左右相对主瓣衰减只有20 dBi左右,过大的天线增益将导致落地EPFD超过规定门限值。此时需要增大隔离角,使得在0°左右的增益相对主瓣衰减可达30 dBi以上,这意味着主瓣只能指向偏离0°很远的地方,大大损失了LEO卫星的覆盖范围。图 6(b)采用Tapering算法对旁瓣电平设置35 dB的衰减约束,波束旁瓣整体上有大幅度的衰减,但同时造成主瓣宽度展宽、增益下降,在俯仰角为0°左右相对主瓣衰减可达30 dBi左右。图 6(c)采用本文所提算法后,波束旁瓣在俯仰角为0°附近形成一条很深的零陷带,相对主瓣衰减50 dBi以上,天线增益的大幅下降使得在干扰隔离区内落地EPFD都能满足ITU规定的门限值,同时主瓣性能并无明显损失,避免了隔离角增大对LEO卫星覆盖范围造成的损失。
3.3 卫星下行链路EPFD仿真为了直观衡量所提策略对EPFD的改善,对不采用低旁瓣算法、采用Tapering算法和采用本文所提算法的单星下行链路EPFD进行仿真分析,定量分析所提策略对干扰规避的有效性。具体仿真参数见表 1,仿真结果如图 7所示。
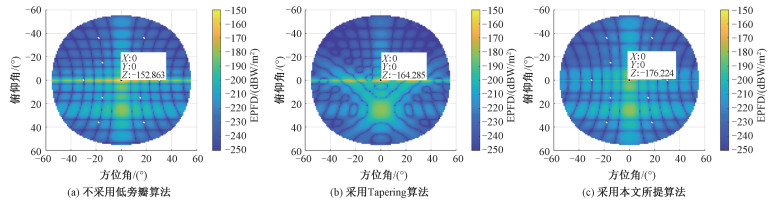
|
Download:
|
| 图 7 采用不同策略的单星EPFD分布 Fig. 7 EPFD distribution of single satellite using different strategies | |
图 7为采用不同策略的单星EPFD分布。设定GSO地面站最小仰角为16.5°,LEO卫星覆盖区的俯仰角和方位角均为±55°。在本文场景下,波束指向(25°, 0°),当不采用低旁瓣算法时,在共线区域(俯仰角为0°)的EPFD仍然超过ITU规定的门限值,表现为在方位角方向的一条“带”,如图 7 (a)所示。采用Tapering算法后,LEO卫星覆盖范围内的EPFD都得到了改善,共线区域刚好满足ITU规定的门限值,如图 7 (b)所示。采用本文所提策略后,图 7 (a)中EPFD超出规定门限值的“干扰抑制带”得到了明显改善,在满足ITU规定门限值的同时还有一定的余量,干扰抑制带外的EPFD分布无明显改变,均不超过ITU规定的门限值,如图 7 (c)所示。
针对上述3种策略取同轨道面的EPFD分布和波束方向图进行对比,如图 8所示。
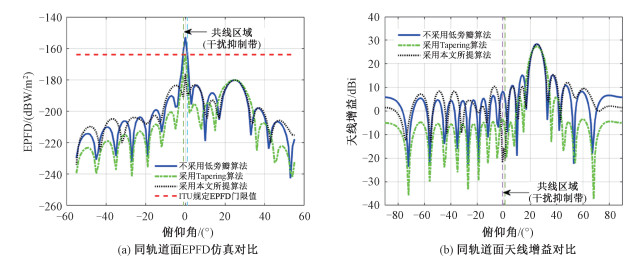
|
Download:
|
| 图 8 同轨道面仿真对比 Fig. 8 Simulation comparison of the same orbital plane | |
图 8(a)为不采用低旁瓣算法、采用Tapering算法和采用本文所提算法的同轨道面EPFD仿真对比图。可以看出不采用低旁瓣算法时在共线区域旁瓣对EPFD的影响最大,俯仰角0°左右的EPFD值超出ITU规定的门限值。采用Tapering算法和本文所提算法均可将共线点附近的EPFD限制在ITU的规定值以下,但本文所提算法对共线点EPFD的改善性能更好。图 8 (b)为不采用低旁瓣算法、采用Tapering算法和采用本文所提算法的天线增益对比图。采用本文所提算法后,天线增益相比原始波束无明显下降、主瓣宽度无展宽,而在干扰抑制带有极低的旁瓣电平,相比Tapering算法优势显著。
4 结论本文从低轨卫星系统中典型的干扰场景入手,针对空间隔离策略解决共线干扰时损失LEO卫星波束有效覆盖范围的问题,提出一种基于发射波束旁瓣零陷的干扰规避策略。定义所有共线点组成的区域为干扰抑制带,将其作为约束目标进行发射波束赋形。考虑到卫星上的计算能力有限且共线区域可由一条“零陷带”来覆盖,将二维面阵按照行、列阵元维度进行划分,化二维全阵列优化算法为一维零陷算法的扩展,算法复杂度和计算量大幅降低,可实时计算,易于在卫星上实现。通过仿真分析发现,旁瓣零陷算法与空间隔离策略的有机结合使得低轨卫星波束覆盖范围内的EPFD都能满足ITU规定的标准,可以更好地实现对GSO地面站的干扰避让,能够有效减少LEO卫星的干扰规避隔离区。
| [1] |
方芳, 吴明阁. 全球低轨卫星星座发展研究[J]. 飞航导弹, 2020(5): 88-92, 95. Doi:10.16338/j.issn.1009-1319.20190258 |
| [2] |
韩锐, 张磊, 刘珊杉. 典型低轨通信星座系统的确定性干扰分析[J]. 数字通信世界, 2020(9): 60-62. Doi:10.3969/J.ISSN.1672-7274.2020.09.022 |
| [3] |
Sharma S K, Chatzinotas S, Ottersten B. Transmit beamforming for spectral coexistence of satellite and terrestrial networks[C]//8th International Conference on Cognitive Radio Oriented Wireless Networks. July 8-10, 2013, Washington, DC, USA. IEEE, 2013: 275-281. DOI: 10.1109/CROWNCom.2013.6636830.
|
| [4] |
Zheng Y H, Sun S L, Rong B, et al. Traffic aware power allocation and frequency reuse for green LTE-A heterogeneous networks[C]//2015 IEEE International Conference on Communications. June 8-12, 2015, London, UK. IEEE, 2015: 3167-3172. DOI: 10.1109/ICC.2015.7248811.
|
| [5] |
Reed A G, Posen M C J. Interference in the fixed satellite service bands between the feeder-links of networks using nongeostationary satellites and network using geostationary satellites[C]//3rd European Conference on Satellite Communications-ECSC-3, 1993. November 2-4, 1993, Manchester, UK. IET, 1993: 251-256.
|
| [6] |
Sharma S K, Chatzinotas S, Ottersten B. Cognitive radio techniques for satellite communication systems[C]//2013 IEEE 78th Vehicular Technology Conference. September 2-5, 2013, Las Vegas, NV, USA. IEEE, 2013: 1-5. DOI: 10.1109/VTCFall.2013.6692139.
|
| [7] |
张泓湜, 蒋伯峰. 基于空间隔离的低轨卫星系统频谱共享方法[J]. 北京航空航天大学学报, 2018, 44(9): 1909-1917. Doi:10.13700/j.bh.1001-5965.2017.0732 |
| [8] |
ITU Radiocommunication (ITU-R). Simulation methodologies for determining statistics of short-term interference between co-frequency, codirectional non-geostationary-satellite orbit fixed-satellite service systems in circular orbits and other non-geostationary fixed-satellite service systems in circular orbits or geostationary-satellite orbit fixed-satellite service networks[S/OL]. (2003-10-08)[2021-12-18]. https://www.itu.int/rec/R-REC-S.1325-3-200310-I/en.html.
|
| [9] |
ITU Radiocommunication (ITU-R). Interference mitigation techniques to facilitate coordination between non-geostationary-satellite orbit mobile-satellite service feeder links and geostationary satellite orbit fixed-satellite service networks in the bands 19.3~19.7 GHz and 29.1~29.5 GHz[S/OL]. (1999-11-30)[2021-12-18]. https://www.itu.int/rec/R-REC-S.1419-0-199911-I/en.html.
|
| [10] |
ITU Radiocommunication (ITU-R). Analytical method to calculate short-term visibility and interference statistics for non-geostationary satellite orbit satellites as seen from a point on the earth's surface[S/OL]. (2002-03-11)[2021-12-18]. https://www.itu.int/rec/R-REC-S.1257-3-200203-I/en.html.
|
| [11] |
Sharma S K, Chatzinotas S, Ottersten B. In-line interference mitigation techniques for spectral coexistence of GEO and NGEO satellites[J]. International Journal of Satellite Communications and Networking, 2016, 34(1): 11-39. Doi:10.1002/sat.1090 |
| [12] |
ITU Radiocommunication (ITU-R). Radio Regulations[S/OL]. (2020-08-19)[2021-12-18]. https://www.itu.int/pub/R-REG-RR-2020.html.
|
| [13] |
Park I, Seo C, Ku H. Sidelobe suppression beamforming using tapered amplitude distribution for a microwave power transfer system with a planar array antenna[J]. Journal of Electromagnetic Engineering and Science, 2022, 22(1): 64-73. Doi:10.26866/jees.2022.1.r.62 |
| [14] |
ITU Radiocommunication (ITU-R). Functional description to be used in developing software tools for determining conformity of non-geostationary-satellite orbit fixed-satellite service systems or networks with limits contained in Article 22 of the Radio Regulations[S/OL]. (2018-01-15)[2021-12-18]. https://www.itu.int/rec/R-REC-S.1503-3-201801-I/en.html.
|
| [15] |
Frost O L. An algorithm for linearly constrained adaptive array processing[J]. Proceedings of the IEEE, 1972, 60(8): 926-935. Doi:10.1109/PROC.1972.8817 |
| [16] |
ITU Radiocommunication (ITU-R). Reference FSS earth-station radiation patterns for use in interference assessment involving non-GSO satellites in frequency bands between 10.7 GHz and 30 GHz[S/OL]. (2001-02-20)[2021-12-18]. https://www.itu.int/rec/R-REC-S.1428-1-200102-I/en.html.
|
 2024, Vol. 41
2024, Vol. 41 


