地热能是起源于地球内部熔融岩浆和放射性物质的无污染天然能源。地热资源根据地热能源采出方式不同可以划分为干热岩型地热资源和水热型地热资源[1]。其中干热岩(hot dry rock, HDR)是指埋藏于地球深部,内部不存在或只存在少量流体,温度高于180℃的高温岩体[1]。增强地热系统(enhanced geothermal system, EGS)是一种通过水力压裂等方式将地下深部低孔、低渗岩体改造成具有较高渗透性的人工地热储层,从中长期经济地采出相当数量的热能并加以利用的技术手段[2]。国际上EGS的开发和研究已持续近50年,目前仍处于试验研发阶段。虽然我国的HDR开发起步相对较晚,不过通过近十年的不断努力也取得了一定的成果[2-4],其中共和盆地HDR开发已经进入场地压裂阶段[5-6]。
数值模拟能很好地反映EGS运行过程,成本低、操作简单,在HDR开发过程中发挥了不可替代的作用。Pandey[7]通过建立被低渗透基质包围的单一均匀裂缝EGS储层流体流动与传热耦合的三维数值模型,研究了注水温度和注水速率对热量提取的影响;Asai等[8]模拟多裂缝EGS的高效工作流程,发现裂缝的水力传导率是影响EGS热提取性能的关键参数;Slatlem等[9]建立了考虑裂缝内非等温流体流动、基质内热交换和力学变形的多裂缝EGS有限元模型,研究表明地热开采过程中的热弹性应变会引起裂缝开度的增加,进而减少系统的采热量;肖鹏等[10]利用ANSYS软件CXF模块建立三维水平井EGS多裂隙模型,分析不同注水量下EGS的运行性能;孙致学等[11]应用几何分形理论构建了不同参数组合的离散裂缝模型,建立了二氧化碳在裂缝内的热流固耦合(thermal-hydraulic-mechanical, THM)模型,确定了影响CO2-EGS运行寿命和开采效率的关键因素;Ma等[12]基于分形和分叉理论,在多井EGS中引入叶状分叉裂缝网络,建立THM模型来研究温度场和压力场的时空演变以及叶状分叉裂缝网络特征对热量开采效率的影响;Figueiredo等[13]在考虑注水压力引起的渗透率变化及平均有效应力变化的基础上,建立THM模型,模拟了有多个预先存在的裂缝带干热岩的热抽采过程;段云星和杨浩[14]以云南腾冲热海热田为地质背景,利用正交设计思想通过数值模拟方法研究井间距、注入流量、注水温度、储层渗透率等因素对EGS采热性能的影响;陈炫沂等[15]基于有限元软件FEFLOW,采用数值模拟的方法分析HDR不同产状人工裂隙带的宽度和渗透率对水热产出能力的影响。这些研究为HDR型地热资源开采提供了重要的指导。
在HDR开采过程中,随着EGS的持续运行,储层温度会变得越来越低,直至生产井流体温度不能满足发电的需要。前人基于数值模拟的技术手段对开采过程中影响热量提取效率和运行寿命的敏感性参数如注水温度、注水速率、裂缝开度、基质渗透率等做了大量研究[16-18],对EGS停止运行后人工储层的温度、压力的自然恢复过程的研究相对较少,而EGS停产后的温度、压力变化对于新的地热井钻探、布置和失去开采价值后地热井的重新利用具有重要意义。
共和盆地恰卜恰地区位于青藏高原东北缘,青海湖以南,高温HDR体呈椭圆形,前人已经对该地区干热岩的地质条件[19]、HDR热物性[20-21]、孔渗特性[22]做出了深入调研。这些研究工作为共和盆地恰卜恰地区HDR开发和恢复过程的数值模拟提供了坚实基础。本文以共和盆地恰卜恰地区HDR开发为背景,在HDR型地热资源开采过程数值模拟的基础上,进一步模拟EGS停止运行后人工储层温度、压力的自然恢复过程。模拟结果有助于深入了解HDR开发后对地质环境所造成的持续影响,能够为该地区后续地热井布井位置提供参考,进而优化共和盆地恰卜恰地区HDR型地热资源开采方案,同时为以后利用废弃的地热井进行二次开发和运营提供指导。
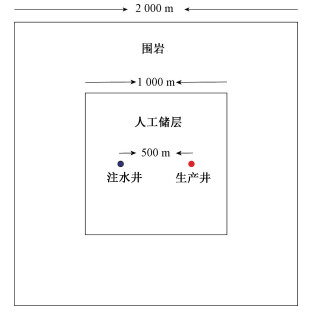
1 模型 1.1 几何模型EGS地下结构复杂,水力压裂以后可以将人工储层看作裂缝和基质两个部分,本文研究的重点在于模拟生产停止后温度恢复过程。该过程缺乏流体循环的参与,裂缝与基质热传递能力的差异不明显,所以对模型做了进一步简化,把人工储层看作等效多孔介质,忽略裂缝和基质的差异。模型由注水井、生产井、人工储层和围岩组成,整个研究区域为2 000 m×2 000 m,注水井、生产井半径0.1 m,间距500 m,人工储层区域为1 000 m×1 000 m,人工储层外侧是围岩(图 1)。
|
Download:
|
| 图 1 几何模型 Fig. 1 Geometrical model | |
在人工储层和围岩中的流动满足达西定律
| $ \boldsymbol{u}=-\frac{\kappa}{\mu} \nabla p. $ | (1) |
其中:u为流体流动速度,κ为渗透率,μ为流体动力黏度,p为压力。
渗流场方程[23]
| $ S \frac{\partial p}{\partial t}+\nabla \cdot \boldsymbol{u}=0. $ | (2) |
其中:S为储水率,p为压力,u为流体流动速度。
温度场方程[23]
| $ C \frac{\partial T}{\partial t}-\lambda \nabla^2 T+C_{\mathrm{w}} \boldsymbol{u} \cdot \nabla T=Q. $ | (3) |
其中: C为多孔介质等效体积热容,λ为多孔介质等效热导率,Cw为流体体积热容,u为流体流动速度,T为温度,Q为放射性热源。
生产井质量通量
| $ -\boldsymbol{n} \cdot \rho_{\rm{w}} \boldsymbol{u}=N_0 . $ | (4) |
其中:n为垂直于井壁的单位矢量,ρw为流体密度,u为流体速度,N0为质量通量。
1.3 边界条件与初始条件 1.3.1 开采过程边界条件与初始条件渗流场初始条件和边界条件如下:注水井压力边界条件为50 MPa,生产井的抽水速率为20 kg/s,假设储层厚度为500 m,生产井边界条件质量通量为(-20/100π)kg/(m2·s)[18]。围岩和储层初始条件为37 MPa,这里假设围岩外部边界压力始终维持初始静水压力,围岩外边界条件为37 MPa[21]。
温度场边界条件与初始条件如下:注水井温度边界条件为313.15 K,生产井为绝热(无热流)的边界条件,模型围岩最外围的边界条件为509.15 K。这里假设围岩边界温度一直保持不变,围岩和储层初始条件为509.15 K[24]。
1.3.2 停产过程边界条件与初始条件开采19 a后的温度场和流体压力场即为停产后的初始条件。注水井和生产井关停,成为无流动边界条件,不再有流体循环。围岩外边界流体压力边界条件为37 MPa,温度条件依然是509.15 K。
1.4 材料参数本文的岩石材料参数参照共和盆地恰卜恰地区的裂隙型花岗岩,把储层等效为均一介质,不考虑水力裂缝的差异[25-26],模型采用的主要材料参数设置如下(表 1):流体密度为1 000 kg/m3[27-28],导热率为0.6 W/(m·K)[27-28],比热容为4 300 J/(kg·K)[27-28],动力黏度为0.001 Pa·s[27-28]。人工储层,渗透率为5×10-14 m2[25-26],孔隙度为5%[25-26],储水率为10-8 Pa-1[27-28]。围岩不考虑水力压裂的影响,渗透率为2.6×10-16 m2[21],孔隙度为2.49%,储水率为10-9 Pa-1[27-28]。不考虑人工储层和围岩之间固体骨架参数的差异,固体骨架密度为2 607 kg/m3[20-21],比热容为754.4 J/(kg·K)[20-21],热导率为2.51 W/(m·K)[20-21],放射性生热率为3.04 μW/m3[29]。
|
|
表 1 EGS有限元模型参数 Table 1 Parameters of the finite element model for EGS |
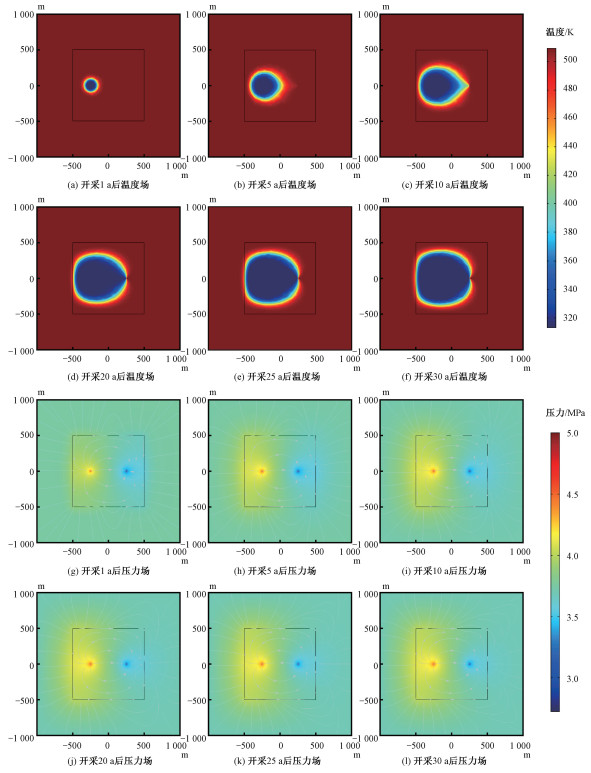
图 2(a)~2(f)分别是EGS运行1、5、10、20、25、30 a以后温度场变化。由该图可以看出温度下降以注水井为中心向外延伸扩展,沿着生产井方向是温度下降的优势方向,冷锋指向生产井。10 a后冷锋已经明显到达生产井;20 a后生产井周围出现明显的温度下降,冷锋到达左侧人工储层的边缘;30 a后人工储层大部分区域都已下降到360 K以下。当产出水温度低于初始温度的60%,也即是141.6 ℃(414.75 K)时,EGS达到运行寿命[14, 30],当产出水温度低于74 ℃(347.15 K)时,将失去开采价值[31]。根据陈必光等[23]提出的产出水温度公式计算可知:19 a后产出水温度为414.51 K,EGS到达运行寿命;68 a后产出水温为347.07 K,HDR人工储层彻底失去开采价值。开采20~30 a期间注水井左侧温度下降范围没有继续延伸扩展,围岩温度几乎没有发生变化,这也说明EGS运行期间,热量交换以热对流为主,热传导的贡献很小。
|
Download:
|
| 图 2 开采过程温度场和压力场演化 Fig. 2 Evolution of temperature field and pressure field during exploitation | |
图 2(g)~2(l)分别是地热开采1、5、10、20、25、30 a后压力场变化。流线方向由注水井指向生产井和围岩的边缘,注水井附近流体压力高于静水压力,生产井附近低于静水压力。随着时间的推移,低于静水压力的范围越来越小,高于静水压力的范围越来越大,不过生产井附近压力始终低于静水压力,并且影响到了围岩。
2.2 EGS停止运行后模拟结果EGS在开采19 a后到达运行寿命,停止地热开采。图 3(a)~3(f)分别是EGS停止运行1、100、500、1 000、2 000、10 000 a后的温度场。由该图可以看出人工储层温度的恢复是十分缓慢的,100 a后以注水井为中心的人工储层大部分区域仍然低于360 K。随着时间的推移温度下降范围有所增大,而整体温度和最低温度不断升高:100 a后人工储层的最低温度仍为313.15 K;500 a后人工储层的最低温度升高到347.90 K,大部分区域温度已经高于360 K;1 000 a后人工储层的最低温度为388.10 K;2 000 a后人工储层的最低温度为433.32 K;10 000 a后最低温度为497.35 K,系统已基本恢复到初始温度。当热储温度介于373.15~423.15 K时为低温地热资源[28],这说明自然恢复1 000 a以后已经废弃的人工储层又重新具备了商业开采价值。

|
Download:
|
| 图 3 EGS停止运行后物理场演化 Fig. 3 Evolution of the physical field after the EGS system stopped operating | |
图 3(g)~3(i)分别是停止开采1、100、1 000 a以后的压力场变化。由该图可以看出人工储层压力场变化很快,开采19 a后压力区间为(27.23,50)MPa,停产1 a后系统压力区间为(36.64,39.41)MPa。最高压力中心和最低压力中心分别位于注水井和生产井一侧的围岩,人工储层内部压力差相较停止开采时的初始状态已经变得很小。这是因为围岩渗透率较低,流体较难进入或者离开围岩,压力变化较慢,而当停止开采以后人工储层由于渗透率较高,很快恢复了平衡。停产100 a后,系统压力区间变为(37,37.72)MPa,此时人工储层与初始压力和围岩边界压力相差不大,可以认为系统压力已达到平衡。到停止开采500 a时,系统压力区间为(37,37.08)MPa,基本无流体流动。
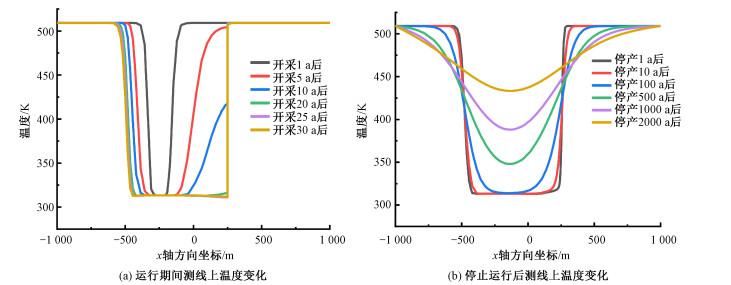
为进一步研究运行期间和停止运行以后系统的温度变化,取一条从左到右经过注水井、生产井中心贯穿储层的测线,分别绘制这条测线开采1、5、10、20、25、30 a后的温度变化(图 4(a))和停产1、10、100、500、1 000、2 000 a后(图 4(b))的温度变化。从图 4(a)可以看出,开采过程中,随着时间的增加温度的下降范围越来越大,但温度下降范围扩展速度越来越小,开采20、25、30 a后温度下降范围大致不变,曲线基本重合。从图 4(b)可以看出,在100 a时最低温度仍然为313.15 K,但最低温度的分布范围已经大大降低;500 a后人工储层温度下降的中心温度已经有明显升高,1 000 a时最低温度为388 K,2 000 a时最低温度为433 K左右;最低温度不断升高,但温度下降范围一直有所扩大,系统温度逐渐接近围岩边界温度。
|
Download:
|
| 图 4 EGS运行期间和停止运行后测线上温度变化 Fig. 4 Temperature change on the measuring line before and after the EGS stops running | |
在HDR开采阶段,人工储层热量交换以热对流为主,此时温度下降过程热传导的作用很小。而在系统温度自然恢复过程中,不再注水、抽水以后,由于没有流体循环,人工储层内流体压力很快达到平衡,整体压力高于静水压力,储存于低温区域的流体向压力较低的围岩边界运移。这个运移是单方向的,不会有高温流体回到低温人工储层区域,因此热对流在人工储层的温度恢复过程中所起到的作用很小。
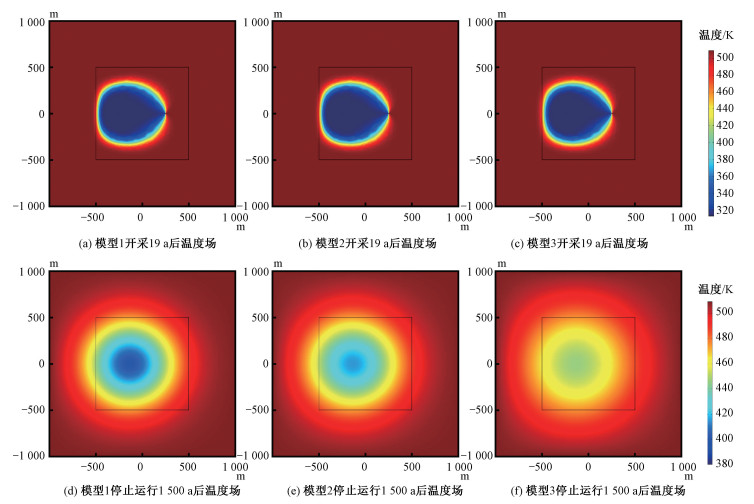
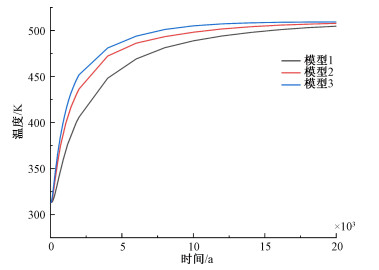
固体骨架热导率是反映HDR热传导能力的一个主要岩石物理参数。为进一步验证热传导在系统温度自然恢复过程中起到的主导作用,本文设计了两个对照模型。以原模型为模型2,固体骨架热导率为2.51 W/(m·K),模型1固体骨架热导率为2 W/(m·K),模型3的固体骨架热导率为4 W/(m·K)。其他参数、初始条件、边界条件保持不变,对模型1、模型3进行求解。图 5(a)~5(c)是模型1~3开采19 a后温度场变化,对照可以看出,开采19 a后不同热导率的温度场基本没有差异。图 5(d)~5(f)是EGS停止运行1 500 a以后的温度场变化,对照可以看出,热导率越低温度恢复得越慢。1 500 a后模型1的最低温度为400.72 K,模型2的最低温度为414.73 K,模型3的最低温度为446.39 K。注水井位于温度下降的中心,取注水井井壁一点(该点为注水井与生产井中心的连线与注水井边界的交点),绘制EGS停止运行以后模型1~3该点温度的变化曲线(图 6)。由该图可以更加直观地看出:HDR岩石骨架热导率越高,EGS停产以后人工储层温度恢复越快。
|
Download:
|
| 图 5 模型1~3开采19 a后和停止运行1 500 a后温度场对照 Fig. 5 Comparison of temperature field of models 1-3 after exploitation for 19 years and out of operation for 1 500 years | |
|
Download:
|
| 图 6 EGS停止运行后模型1~3注水井井壁一点温度随时间变化 Fig. 6 Changes of temperature at one point on the well wall of water injection wells in models 1-3 after EGS stopped running | |
以共和盆地恰卜恰地区HDR开发为背景,基于对HDR生产过程中温度下降及停产后温度恢复过程的热-多孔介质孔隙流体耦合数值模拟研究结果,可以得到以下结论:
1) HDR开采人工储层温度下降过程是非常快的,围岩热传导补充的热量远远不足以弥补从人工储层中提取的热量。不到10 a生产井附近温度就出现明显下降,19 a后就已经达到开发寿命;
2) EGS停止运行以后HDR温度的自然恢复过程是非常缓慢的,1 000 a以后开始重新具备一定的地热开采价值。大约10 000 a后,人工储层温度才整体恢复到初始值,依靠自然恢复很难在短期内重启地热开发进程,需要研究一些人工恢复技术以加快温度恢复进程;
3) HDR开发过程中的热量交换方式以热对流为主,而停止开采以后HDR人工储层的自然恢复过程以热传导为主,HDR固体骨架热导率越高,温度恢复越快。
感谢石耀霖教授和蔡永恩教授对本文研究的指导和帮助,感谢周元泽教授对本文初稿的修改。| [1] |
汪集旸, 胡圣标, 庞忠和, 等. 中国大陆干热岩地热资源潜力评估[J]. 科技导报, 2012, 30(32): 25-31. Doi:10.3981/j.issn.1000-7857.2012.32.003 |
| [2] |
许天福, 胡子旭, 李胜涛, 等. 增强型地热系统: 国际研究进展与我国研究现状[J]. 地质学报, 2018, 92(9): 1936-1947. Doi:10.3969/j.issn.0001-5717.2018.09.012 |
| [3] |
甘浩男, 王贵玲, 蔺文静, 等. 增强型地热系统环境地质影响现状研究与对策建议[J]. 地质力学学报, 2020, 26(2): 211-220. Doi:10.12090/j.issn.1006-6616.2020.26.02.020 |
| [4] |
关健, 方石. 地热系统的概念与传热机制综述[J]. 地质与资源, 2021, 30(2): 207-213, 206. Doi:10.13686/j.cnki.dzyzy.2021.02.013 |
| [5] |
徐胜强, 张旭东, 张保平, 等. 测斜仪监测技术在共和盆地干热岩井压裂中的应用研究[J]. 探矿工程(岩土钻掘工程), 2021, 48(2): 42-48. Doi:10.12143/j.ztgc.2021.02.006 |
| [6] |
周健, 曾义金, 陈作, 等. 青海共和盆地干热岩压裂裂缝测斜仪监测研究[J]. 石油钻探技术, 2021, 49(1): 88-92. Doi:10.11911/syztjs.2020139 |
| [7] |
Pandey S N. A three-dimensional coupled thermal-hydro model for enhanced geothermal systems[J]. International Journal of Renewable Energy Research, 2016, 6: 1516-1523. Doi:10.20508/ijrer.v6i4.4773.g6941 |
| [8] |
Asai P, Panja P, McLennan J, et al. Efficient workflow for simulation of multifractured enhanced geothermal systems (EGS)[J]. Renewable Energy, 2019, 131: 763-777. Doi:10.1016/j.renene.2018.07.074 |
| [9] |
Slatlem Vik H, Salimzadeh S, Nick H M. Heat recovery from multiple-fracture enhanced geothermal systems: The effect of thermoelastic fracture interactions[J]. Renewable Energy, 2018, 121: 606-622. Doi:10.1016/j.renene.2018.01.039 |
| [10] |
肖鹏, 闫飞飞, 窦斌, 等. 增强型地热系统水平井平行多裂隙换热过程数值模拟[J]. 可再生能源, 2019, 37(7): 1091-1099. Doi:10.13941/j.cnki.21-1469/tk.2019.07.023 |
| [11] |
孙致学, 姜传胤, 张凯, 等. 基于离散裂缝模型的CO2增强型地热系统THM耦合数值模拟[J]. 中国石油大学学报(自然科学版), 2020, 44(6): 79-87. Doi:10.3969/j.issn.1673-5005.2020.06.010 |
| [12] |
Ma Y Y, Li S B, Zhang L G, et al. Analysis on the heat extraction performance of multi-well injection enhanced geothermal system based on leaf-like bifurcated fracture networks[J]. Energy, 2020, 213: 118990. Doi:10.1016/j.energy.2020.118990 |
| [13] |
Figueiredo B, Tsang C F, Niemi A. The influence of coupled thermomechanical processes on the pressure and temperature due to cold water injection into multiple fracture zones in deep rock formation[J]. Geofluids, 2020, 2020: 8947258. Doi:10.1155/2020/8947258 |
| [14] |
段云星, 杨浩. 增强型地热系统采热性能影响因素分析[J]. 吉林大学学报(地球科学版), 2020, 50(4): 1161-1172. Doi:10.13278/j.cnki.jjuese.20190041 |
| [15] |
陈炫沂, 姜振蛟, 徐含英, 等. 共和盆地干热岩体人工裂隙带结构的控热机理与产能优化[J]. 水文地质工程地质, 2022, 49(1): 191-199. Doi:10.16030/j.cnki.issn.1000-3665.202104058 |
| [16] |
Sun Z X, Zhang X, Xu Y, et al. Numerical simulation of the heat extraction in EGS with thermal-hydraulic-mechanical coupling method based on discrete fractures model[J]. Energy, 2017, 120: 20-33. Doi:10.1016/j.energy.2016.10.046 |
| [17] |
Lei Z H, Zhang Y J, Zhang S Q, et al. Electricity generation from a three-horizontal-well enhanced geothermal system in the Qiabuqia geothermal field, China: slickwater fracturing treatments for different reservoir scenarios[J]. Renewable Energy, 2020, 145: 65-83. Doi:10.1016/j.renene.2019.06.024 |
| [18] |
Liu H J, Wang H W, Lei H W, et al. Numerical modeling of thermal breakthrough induced by geothermal production in fractured granite[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2020, 12(4): 900-916. Doi:10.1016/j.jrmge.2020.01.002 |
| [19] |
张盛生, 张磊, 田成成, 等. 青海共和盆地干热岩赋存地质特征及开发潜力[J]. 地质力学学报, 2019, 25(4): 501-508. Doi:10.12090/j.issn.1006-6616.2019.25.04.048 |
| [20] |
张超, 张盛生, 李胜涛, 等. 共和盆地恰卜恰地热区现今地热特征[J]. 地球物理学报, 2018, 61(11): 4545-4557. Doi:10.6038/cjg2018L0747 |
| [21] |
雷治红. 青海共和盆地干热岩储层特征及压裂试验模型研究[D]. 长春: 吉林大学, 2020.
|
| [22] |
王世永. 青海共和盆地干热岩岩体力学特征及渗透特性研究[D]. 北京: 中国石油大学(北京), 2019.
|
| [23] |
陈必光, 宋二祥, 程晓辉. 二维裂隙岩体渗流传热的离散裂隙网络模型数值计算方法[J]. 岩石力学与工程学报, 2014, 33(1): 43-51. Doi:10.13722/j.cnki.jrme.2014.01.005 |
| [24] |
马哲民, 谭现锋, 郝俊杰, 等. 多种测温方法在青海共和干热岩GR1井中的应用[J]. 探矿工程(岩土钻掘工程), 2020, 47(12): 42-48. Doi:10.12143/j.tkgc.2020.12.007 |
| [25] |
岳高凡, 邓晓飞, 邢林啸, 等. 共和盆地增强型地热系统开采过程数值模拟[J]. 科技导报, 2015, 33(19): 62-67. Doi:10.3981/j.issn.1000-7857.2015.19.010 |
| [26] |
丁军锋, 王世民. 增强型地热系统的多区域多物理场耦合三维数值模拟[J]. 中国科学院大学学报, 2019, 36(5): 694-701. Doi:10.7523/j.issn.2095-6134.2019.05.015 |
| [27] |
孙致学, 徐轶, 吕抒桓, 等. 增强型地热系统热流固耦合模型及数值模拟[J]. 中国石油大学学报(自然科学版), 2016, 40(6): 109-117. Doi:10.3969/j.issn.1673-5005.2016.06.014 |
| [28] |
崔翰博, 唐巨鹏, 姜昕彤. 渗透率对干热岩开采过程储层变化规律的影响[J]. 水文地质工程地质, 2020, 47(1): 171-180. Doi:10.16030/j.cnki.issn.1000-3665.201811014 |
| [29] |
张超, 胡圣标, 宋荣彩, 等. 共和盆地干热岩地热资源的成因机制: 来自岩石放射性生热率的约束[J]. 地球物理学报, 2020, 63(7): 2697-2709. Doi:10.6038/cjg2020N0381 |
| [30] |
张伟, 孙江, 曲占庆, 等. 高温地热开采热流固耦合模型及综合评价方法[J]. 地球物理学进展, 2019, 34(2): 668-675. Doi:10.6038/pg2019CC0445 |
| [31] |
John W L, Bloomquist R G, Tonya L B, et al. The united states of America country update[C]//Proceedings World Geothermal Congress 2005. Antalya, Turkey: Transactions-geothermal Resources Council, 2005: 1-19.
|
 2024, Vol. 41
2024, Vol. 41 


