2. 中国科学院上海微系统与信息技术研究所, 上海 200050
2. Shanghai Institute of Microsystem and Information Technology, Chinese Academy of Sciences, Shanghai 200050, China
无线传感器网络(wireless sensor network,WSN)在通信领域发挥至关重要的作用。由于传感器价格低廉,具备感知环境中各种物理因素的能力,同时也可以传输和处理数据。通常将数百到数千个传感器随机部署在空间中,每个传感器监测并收集温度、声音、压力等信息,传输给其他传感器节点或者基站[1]。WSN现已被应用于工业、气象、医疗等领域[2]。然而,传感器的能量是有限的,能量耗尽后会影响数据收集和整个WSN的通信。因此,降低传感器能耗,有效延长网络生存周期是设计WSN的重要目标。现有研究中,分簇路由算法是常用且能有效解决该问题的一类算法。其将区域中的所有传感器节点分为多个簇,每个簇中选取一个节点作为簇首节点,簇首节点收集数据并通过多跳路由将数据传输到基站。
低功耗自适应分簇路由算法(low energy adaptive clustering hierarchy, LEACH)[3]是最早提出的经典分簇路由协议,每轮每个节点随机生成一个数值,与阈值进行比较来判断其是否可以成为簇首节点,簇首节点直接与基站通信。然而随机选举簇首节点会导致分簇不均衡,网络能耗不均衡。LEACH-C[4]协议是对LEACH协议的后续改进,它不采用随机选举簇首节点,而是选择能量更高的节点作为簇首节点收集簇内数据,降低了通信成本。
然而,对随机分布的传感器节点进行分簇和路由可认为是NP-hard问题[5],通过LEACH及其改进协议获得最优解存在局限性。现有研究大多通过引入元启发式算法来寻求最佳聚类和路由,进而降低传感器网络整体能耗,延长网络寿命。文献[6]引入遗传算法优化得到初始聚类中心后,利用模糊C均值聚类算法形成分簇,簇首选举时综合考虑节点的剩余能量,与基站和其他节点的距离等因素,能够有效降低网络能耗,提高网络均衡性。文献[7]提出基于改进粒子群优化算法的分簇路由算法,引入粒子群优化算法和新的适应度函数选举出最优的簇首节点,设计了基于最小生成树算法为簇首节点搜索到基站的数据传输路径,仿真结果表明其降低了网络能耗、提高了网络吞吐量。文献[8]引入蚁群算法在WSN中寻找最优路由,利用角度因子和距离因子优化启发信息函数,并引入最优路径度量公式改进信息素更新策略,有效均衡网络中节点能耗,延长网络寿命。文献[9]提出基于鲸鱼算法的网络分簇路由协议,利用鲸鱼算法选举出剩余能量高和分布均匀的簇首节点,通过设置能量阈值减少簇首节点更换频次,降低了分簇能耗,但该协议的簇首节点直接将收集和融合的数据传输给基站,会加剧远离基站的簇首节点的能量消耗。
上述研究表明通过引入启发式优化算法来解决WSN中的分簇和路由问题,能够有效降低网络能耗,延长网络寿命。本文在此基础上,提出生物地理学优化算法改进K-means算法的分簇路由算法BBOK-GA。BBOK-GA通过使用生物地理学优化算法克服K-means算法对初始聚类中心的敏感,并且基于距离和能量设计新的适应度函数来选举剩余能量高和分布均匀的最优簇首节点。为解决簇首节点直接将数据发送到基站消耗过多能量太早死亡的问题,引入遗传算法搜索最佳簇间路由,从而均衡网络能耗,延长网络寿命。
1 系统模型 1.1 网络模型在真实WSN的应用场景,通过随机部署传感器节点来持续监测环境,传感器将收集到的数据发送给远离部署场景的基站。网络模型考虑如下假设:
1) 所有传感器节点和基站都是固定放置的,基站能量不受限制。
2) 默认为同构网络,所有传感器节点具有相同的初始能量。
3) 所有传感器节点知道自己的节点位置和节点ID。
4) 所有的传感器节点能够以传感器模式进行,监测数据并传输给簇首节点,也能够以簇首模式进行,收集簇内节点的数据后压缩融合,通过单跳或者多跳传输给基站。
5) 所有传感器节点可以感知剩余能量和计算到目标节点的距离。
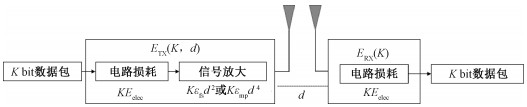
1.2 能量模型参照LEACH算法使用的能量模型[3],如图 1所示,使用自由空间模型和多径衰落信道模型计算WSN中传感器节点发送和接收数据的能量耗散。
|
Download:
|
| 图 1 能量模型 Fig. 1 Energy model | |
发送K bit数据传输距离d所消耗的能量可以按照如下公式计算:
| $ E_{\mathrm{TX}}(K, d)=\left\{\begin{array}{l} K E_{\text {elec }}+K \varepsilon_{\mathrm{fs}} d^2, d<d_0, \\ K E_{\text {elec }}+K \varepsilon_{\mathrm{mp}} d^4, d \geqslant d_0 . \end{array}\right. $ | (1) |
其中:εfs是自由空间传输的能量耗散,εmp是多径衰落传输的能量耗散,Eelec是信号发送电路单元发送数据产生的能量耗散,d0是距离阈值,距离阈值可用下式计算:
| $ d_0=\sqrt{\frac{\varepsilon_{\mathrm{fs}}}{\varepsilon_{\mathrm{mp}}}} . $ | (2) |
接收K bit数据消耗的能量为
| $ E_{\mathrm{RX}}(K)=K E_{\text {elec }} . $ | (3) |
传感器节点对数据进行融合时也需要消耗能量,对K bit数据进行融合产生的能量耗散为
| $ E_{\mathrm{A}}(K)=K E_{\mathrm{DA}} . $ | (4) |
其中EDA表示1bit数据融合需要的能量。
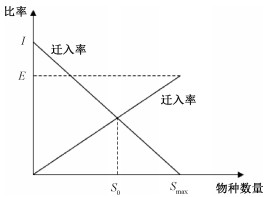
2 生物地理学优化算法生物地理学优化算法是Simon在2008年基于生物地理学的种群迁移数学模型提出的优化算法[10],模拟了物种如何从一个栖息地迁移到另一个栖息地,新物种如何出现以及灭绝的过程。栖息地适宜指数(habitat suitability index, HSI)表示生物物种居住的适宜程度,适应性指数变量(suitable index variable, SIV)表示可居住性,SIV可看作栖息地的自变量,HSI可看作因变量。高HSI的栖息地生物物种多,物种迁移率低;低HSI的栖息地生物物种少,迁移率高。使用生物地理学解决优化问题时,可通过HSI值量化解决方案的适用性。类似于其他种群算法中的适应度值,高HSI值的解决方案更优,还可与低HSI解决方案共享其优良的特性,这种方法有助于提高解决方案的质量[11]。单栖息地的物种模型如图 2所示,2条直线分别表示迁入率λ、迁出率μ和物种数量的关系。当栖息地中物种数量为0时,迁移率最大为I,迁出率最小为0。随着物种数量增加,迁入率下降,迁出率上升。当物种数量达到最大值Smax时迁入率为0,迁出率最大为E。物种数量为S0时,迁入率和迁出率相等,达到平衡。
PS为栖息地中有S个物种的概率,当时间从t到t+Δt时PS会按下式变化
| $ \begin{gathered} P_S(t+\Delta t)=P_S(t)\left(1-\lambda_S \Delta t-\mu_S \Delta t\right)+ \\ P_{S-1} \lambda_{S-1} \Delta t+P_{S+1} \lambda_{S+1} \Delta t . \end{gathered} $ | (5) |
当Δt趋于0时,用
| $ \dot{P}_S= \begin{cases}-\left(\lambda_S+\mu_S\right) P_S+\mu_{S+1} P_{S+1}, & S=0, \\ -\left(\lambda_S+\mu_S\right) P_S+\lambda_{S-1} P_{S-1}+\mu_{S+1} P_{S+1}, & 1 \leqslant S \leqslant S_{\max }-1, \\ -\left(\lambda_S+\mu_S\right) P_S+\lambda_{S-1} P_{S-1}, & S=S_{\max } .\end{cases} $ | (6) |
其中:μS, λS为栖息地有S个物种时的迁入率和迁出率,可通过图 2计算得到:
| $ \mu_S=\frac{E_S}{S_{\text {max }}}, $ | (7) |
| $ \lambda_S=\boldsymbol{I}\left(1-\frac{S}{S_{\max }}\right) . $ | (8) |
|
Download:
|
| 图 2 单栖息地的物种模型 Fig. 2 Species model of single habitat | |
生物地理学优化算法包含迁移操作和变异操作。
2.1 迁移操作当处理优化问题时,存在多个解决方案,高HSI的栖息地代表好的解决方案,低HSI的栖息地代表差的解决方案。物种在不同的栖息地之间的迁移操作,可以理解为不同的解决方案之间共享信息,这样优良解会把自身的特性共享给较差解,较差解在迭代过程中有较大概率向优良解学习,整体向最优解收敛。当一个解决方案Si需要被更改时,根据其迁入率λ计算得到其适应性指数变量中需要更改的分量,利用其他解决方案Sj的迁出率μ计算将适应性指数变量迁移到解决方案Si的概率。与其他群体优化算法一样,生物地理学优化算法的迁移操作加入了精英主义,以便在群体中保留最佳的解决方案,防止最优解决方案的优良特性在迁移过程中丢失。
2.2 变异操作发生突发事件时,栖息地的HSI值会突然变化,生物地理学优化算法将其建模为SIV突变,并通过物种数量概率
| $ m(S)=m_{\max }\left(\frac{1-\dot{P}_S}{P_{\text {max }}}\right) . $ | (9) |
其中:mmax为最大变异率,是可以设置的参数,其值较大时,发生突变的栖息地更多;Pmax是最大物种数量概率,可通过式(6)计算得到。变异操作不仅可以使低HSI的栖息地得到改进,也可以使高HSI的栖息地更好地提升优良特性,一定程度上可以避免优化算法进入局部最优。
3 BBOK-GA路由算法BBOK-GA基于轮次机制运行,每一轮包含成簇阶段和数据传输阶段。成簇阶段,基站广播请求信息,收集区域内所有传感器节点的位置信息。通过基于生物地理学优化算法改进K-means选出最佳簇首节点,簇首节点广播信息,非簇首节点加入相应的簇。在数据传输阶段,簇首节点处采用时分多址技术与成员节点进行通信,收集并融合数据,基于遗传算法选择最优的传输路径将数据传输到基站。
3.1 成簇阶段 3.1.1 适应度函数在成簇阶段,选取最佳的簇首节点有利于减少WSN的能耗,延长WSN的存活时间。利用群智能优化算法解决簇首选举问题时,应设计合理的适应度函数。本文基于距离和能量因素提出一种新的适应度函数。
相较非簇首节点而言,簇首节点需要收集并融合簇内所有传感器节点的数据,距离基站较远时还需通过多跳路由将数据传输到基站,所以优先选取能量高的节点作为簇首节点。假定WSN中有n个节点,其中有m个簇首节点,n-m个非簇首节点,给出如下的目标函数f1,f1值越小,说明簇首节点的能量越高。
| $ f_1=\frac{\sum\limits_{j=1}^{n-m} E\left(\mathrm{NCH}_j\right)}{\sum\limits_{i=1}^m E\left(\mathrm{CH}_i\right)}, $ | (10) |
其中:E(CHi)是簇首节点的能量,E(NCHj)是非簇首节点的能量。
当簇首节点与其簇内节点的距离较近时,簇间通信消耗的能量更少,同时簇首节点之间距离不宜太近,有利于在WSN整个区域形成均匀的分簇。基于簇首节点与簇内节点的距离和簇首节点间的距离设计目标函数f2
| $ f_2=\frac{\sum\limits_{i=1}^m \sum\limits_{\text {node } \in\left\|\mathrm{CH}_i\right\|} d\left(\text { node }, \mathrm{CH}_i\right) / \mathrm{CH}_i}{\sum\limits_{i=1}^m \sum\limits_{k \in[1, m], k \neq i} d\left(\mathrm{CH}_i, \mathrm{CH}_k\right) / C_m^2}, $ | (11) |
其中:‖CHi‖是第i个簇中节点总数,d(node, CHi)是第i个簇中非簇首节点到簇首节点的距离,Cm2是从m个簇首节点中选取2个簇首节点计算距离的方案数,d(CHi, CHk)是簇首节点之间的距离。
同时,选取最佳簇首节点时应考虑簇首节点与基站之间的距离,离基站距离相对较近时,把数据传输到基站消耗的能量就越少。目标函数f3公式如下
| $ f_3=\frac{\sum\limits_{i=1}^m d\left(\mathrm{CH}_i, \mathrm{BS}\right) / m}{\sum\limits_{i=1}^n d(\text { node }, \mathrm{BS}) / n}, $ | (12) |
其中:d(CHi, BS)是簇首到基站的距离, d(node, BS)是非簇首节点到基站的距离。
计算适应度函数数值时,将3个目标函数f1、f2和f3线性组合转换为单目标函数计算:
| $ f=\alpha_1 f_1+\alpha_2 f_2+\alpha_3 f_3 . $ | (13) |
其中:α1、α2、α3为权重参数,且满足
| $ \sum\limits_{i=1}^3 \alpha_i=1, \alpha_i \in(0,1). $ | (14) |
K-means是经典的无监督聚类算法,可用于将无线传感器网络中随机分布的传感器节点分成多个聚类[12]。但K-means聚类算法在初始化时随机选择聚类中心,这会对算法收敛情况产生很大影响,导致陷入局部最优。生物地理学优化算法是一种针对全局优化问题的算法,通过迁移操作和变异操作寻求最优的解决方案。通过使用生物地理学优化算法可在传感器覆盖空间内迭代找到最优的簇首节点集,将其作为K-means聚类算法的初始聚类中心,避免K-means算法迭代时陷入局部最优。K-means算法在已经找到的初始聚类中心附近的小范围成簇中寻找更优的簇首节点,再完成非簇首节点入簇过程。
基于生物地理学优化算法改进K-means算法寻找最优簇首时,首先需要进行参数初始化,初始化L个栖息地H1, H2, …, HL, 其中Hi是n维行向量,n为区域内传感器节点数,Hi=(Hi1, Hi2, …, Hin), 设置m为最优簇首数目,Maxgen为最大迭代次数。再通过计算式(13)表示的适应度函数,得到每个栖息地的HSI值。将栖息地H1, H2, …, HL按HSI值从小到大排序,保留少量最优栖息地作为精英群体。将每个栖息地Hi映射到物种数量S,计算迁入率λi和迁出率μi。完成上述操作后,需对栖息地进行迁移操作和变异操作。首先对栖息地两两之间进行迁移操作, 选择迁入率为λi的栖息地Hi,迁出率为μj的栖息地Hj。产生随机数r1, r1∈(0, 1), 当r1小于μj时,从1到n中随机挑选m个互不相等的正整数组成位置向量p=(p1, p2, p3, …, pm)。交换栖息地Hpki和Hjpk,k∈1, 2, …m。迁移操作后再对L个栖息地进行变异操作。根据栖息地Hi的迁入率λi和迁出率λj计算出栖息地Hi的变异概率Pi,选择出需要变异的栖息地Hi,随机选择栖息地的一个分量,该分量值若为0,则用1替代,若为1,则用0代替。重复计算适应度值操作和迁移变异操作直到达到最大迭代次数。完成迭代后计算当前L个栖息地的HSI值,进行排序,最优的栖息地Hbest=(Hbest1, Hbest2, …, Hbestn), 若Hbesti值为1,则代表第i个节点为簇首节点,若值为0,则为非簇首节点。上述过程通过生物地理学优化算法得到了最佳簇首,将其作为K-means聚类算法的初始聚类中心,非簇首节点根据欧几里得距离选择离其最近的初始聚类中心,加入所在簇。对于形成的每个簇,按照下式重新计算坐标值作为聚类中心:
| $ \mathrm{CH}_i(X, Y)=\left(\frac{1}{\left\|\mathrm{CH}_i\right\|} \sum\limits_{j=1}^{\mathrm{CH}_i} x_i, \frac{1}{\left\|\mathrm{CH}_i\right\|} \sum\limits_{j=1}^{\mathrm{CH}_i} y_i\right) . $ | (15) |
其中:(xi, yi)是传感器节点的坐标,‖CHi‖是第i个簇中传感器节点的数量,CHi(X, Y)是第i个簇的中心坐标值。重复如上计算,直到达到收敛条件或者最大迭代次数。选择距离上述所得中心坐标值最近的传感器节点作为簇首节点,其他传感器节点根据欧氏距离加入簇首节点所在簇,完成成簇阶段。
3.2 数据传输阶段在数据传输阶段,簇首节点收集并融合簇内节点传来的数据后,还需将数据传输到基站。若采用单跳传输,远离基站的簇首节点会消耗过多能量,减少网络寿命。
3.2.1 路径评估函数本文采用遗传算法搜索簇首节点到基站的最优传输路径,基于距离因子和节点度因子设计了路径评估函数。
簇首节点的数据经中继簇首节点多跳转发传输到基站,选取中继簇首节点时,距离越远,消耗的能量越多。根据距离因子设计如下目标函数p1
| $ p_1=\frac{\sum\limits_{i=1}^m\left(\operatorname{dis}\left(\mathrm{CH}_i, \mathrm{NH}\right)+\operatorname{dis}(\mathrm{NH}, \mathrm{BS})\right)}{\sum\limits_{i=1}^m \operatorname{dis}\left(\mathrm{CH}_i, \mathrm{BS}\right)}, $ | (16) |
其中:dis(CHi, NH)是簇首节点到下一跳节点的距离,dis(NH, BS)是下一跳节点到基站的距离,簇首节点到基站的距离为dis(CHi, BS)。
同时,若簇首节点其簇内节点数较多,簇内通信开销大,不宜被选为中继节点。考虑中继节点的节点度因子设计目标函数p2, 其中∑‖NH‖是簇首节点的下一跳簇首节点簇内节点总数。
| $ p_2=\frac{\sum\limits_{i=1}^m \sum\limits_{j=1}^n\|\mathrm{NH}\|}{m n} . $ | (17) |
2个目标函数互不冲突,通过权重因子将其线性组合转化为单目标函数求解:
| $ p=\beta_1 p_1+\beta_2 p_2 . $ | (18) |
其中: β1, β2是权重因子,满足
| $ \sum\limits_{i=1}^2 \beta_i=1, \beta_i \in(0,1) . $ | (19) |
遗传算法是由John Holland提出的模拟自然界生物进化全过程的元启发式算法, 用来解决优化问题[13]。遗传算法随机生成一组可能解作为初始群体,个体解决方案由称为染色体的数组表示,适应度函数用来评估每个个体解决方案的性能。在初始群体后,随机选择2个染色体作为父母染色体,交换其染色体信息形成新的子染色体,称为交叉过程。子染色体进行突变操作来恢复一些优良特性,结束后计算适应度值并与父母染色体比较,保留这代最优的结果。遗传算法被用于解决WSN的分簇和路由的优化问题[14]。
在数据传输阶段,本文基于遗传算法为簇首节点选择最佳传输路径的算法步骤如下所示:
步骤1 编码,对成簇阶段得到的m个簇首节点编号。
步骤2 种群初始化,产生初始种群作为起始解,种群中包含m个染色体。
步骤3 基于路径评估函数对初始化种群中每个染色体进行计算。
步骤4 选择操作,按照一定概率从旧群体中选择染色体加入到新群体中,概率计算和个体的路径评估函数值有关。
步骤5 交叉操作,使用部分映射交叉,将交叉的父代两两分组,随机选取2个位置,对父代2个位置之间的数据进行交叉交换。交叉后,若染色体中有重复的簇首编号,采用部分映射的方法消除冲突。
步骤6 变异操作,随机产生2个位于1和m之间的正整数,对这2个正整数位置上的数据进行对调。
步骤7 重复步骤3~6直到达到最大迭代次数。
3.3 算法复杂度分析成簇阶段,使用生物地理学优化算法时涉及计算个体适应度值以及迁移变异操作。假设种群个数为M,传感器节点个数为N,则计算适应度函数的算法复杂度为O((M+N)2log(M+N))。迁移和变异操作的算法复杂度为O(M)。数据传输阶段,采用遗传算法寻找最优传输路径,假设种群个数为P,迭代次数为R,算法复杂度为O(P×R)。所以,本文提出的BBOK-GA算法的最差算法复杂度为O((M+N)2log(M+N))+2O(M)+O(P×R)。
4 仿真实验 4.1 参数设置本文通过MatlabR2020a对BBOK-GA路由算法仿真,将200个传感器节点随机分布在100m×100m的正方形区域内,根据表 1的仿真参数搭建仿真场景,并与LEACH[3]、LEACH-C[4]、K-GA[15]算法进行对比来验证该算法的性能。
|
|
表 1 实验参数 Table 1 Simulation parameters |
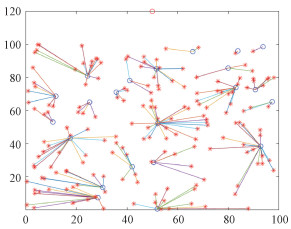
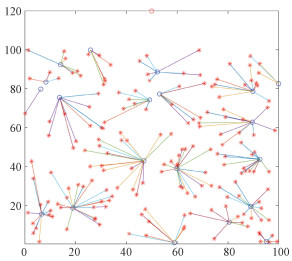
图 3是LEACH成簇结果图。由于LEACH协议中根据阈值随机选取簇首节点,可以明显看到某些簇首节点下有20个左右的簇内节点,而某些簇首节点下仅有1个簇内节点,这种情况下成簇极不均匀。图 4是结合了生物地理学优化算法和K-means算法的成簇结果,可以看到成簇较为均匀,对于边界处的节点也有较好的成簇结果,极大簇和极小簇的数量也相应减少,簇首节点分布也较为均匀,克服了K-means算法对初始聚类中心敏感的问题。
|
Download:
|
| 图 3 LEACH成簇结果 Fig. 3 Clustering result diagram of LEACH | |
|
Download:
|
| 图 4 BBOK-GA成簇结果 Fig. 4 Clustering result diagram of BBOK-GA | |
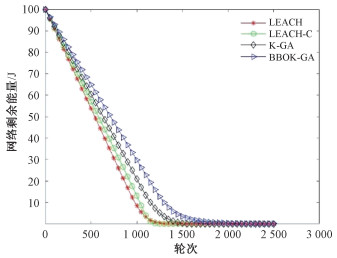
网络剩余能量是指网络中所有存活的传感器节点的能量总和。图 5为BBOK-GA和LEACH、LEACH-C、K-GA的网络剩余能量对比。BBOK-GA的网络剩余能量始终高于另外3种算法,同时能量下降更加缓慢,WSN在第1835轮才耗尽网络所有能量。由于BBOK-GA算法中适应度函数和路径评估函数设计综合考虑了距离、能量因子和节点度等因素,同时,引入生物地理学优化算法优化K-means通过多次迭代优化,快速收敛得到最优簇首解,减少了整个网络的总传输距离,有利于均衡网络中所有传感器节点的能量消耗,进而延长能量耗尽的执行轮次。
|
Download:
|
| 图 5 网络剩余能量对比 Fig. 5 Comparison of network remaining energy | |
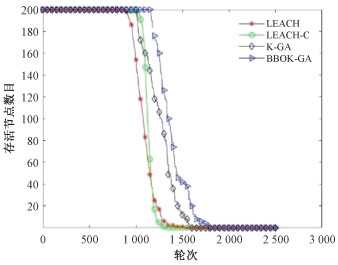
网络生存周期定义为网络从开始工作到传感器节点死亡的时间间隔,是判断WSN路由算法性能的重要指标。图 6显示了LEACH、LEACH-C、K-GA和BBOK-GA等4种算法不同轮次时的存活节点情况。BBOK-GA生命周期相较于LEACH、LEACH-C、K-GA分别延长52.8%、41%和17.1%。应用BBOK-GA算法时,网络中存活节点个数始终多于另外3种,得益于应用了BBO算法对K-means进行优化,防止K-means算法进入局部最优情况,从而选举出分簇均匀, 剩余能量高的簇首节点。同时,BBOK-GA基于遗传算法找到从簇首节点到基站的最佳传输路径,避免簇首节点之间将数据传输到基站消耗过多能量,减少了每一轮中选举簇首节点的能量消耗。
|
Download:
|
| 图 6 网络存活节点数目对比 Fig. 6 Comparison of number of alive nodes | |
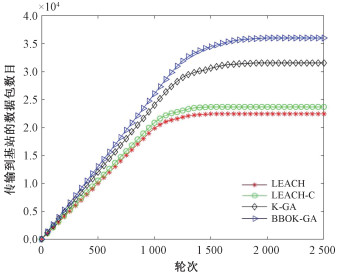
图 7是仿真场景下应用LEACH、LEACH-C、K-GA和BBOK-GA等4种算法时,基站接收到的数据包总数,每个数据包包含4000bit数据。应用BBOK-GA时,基站接收到最多的数据包,网络吞吐量指标更加优越。因为相较于另外3种分簇路由算法,BBOK-GA在成簇阶段和数据传输阶段都采用改进群体智能算法进行了优化。成簇阶段选举出的簇首节点剩余能量更高,距离簇内节点和基站更近,传输数据时消耗更少的能量。数据传输阶段中,选取簇首节点到基站的传输路径时考虑了多跳距离和中继节点的节点度因子,通过最优路径传输时,有效地节约了中继节点转发数据消耗的能量,网络生存期更长,同一轮次存活节点数更多,传输到基站的数据包也就更多。
|
Download:
|
| 图 7 网络吞吐量对比 Fig. 7 Comparison of number of network throughput | |
为降低传感器节点能耗,延长WSN寿命,本文提出BBOK-GA分簇路由算法。首先基于生物地理学优化算法改进K-means选举最优簇首节点并成簇,然后基于遗传算法为簇首节点搜索到基站的最佳数据传输路径。仿真结果表明,本文提出的算法BBOK-GA与LEACH、LEACH-C、K-GA相比将网络生存周期分别延长52.8%、41%和17.1%, 均衡了WSN能耗,提高了网络吞吐量。
| [1] |
钱志鸿, 王义君. 面向物联网的无线传感器网络综述[J]. 电子与信息学报, 2013, 35(1): 215-227. Doi:10.3724/SP.J.1146.2012.00876 |
| [2] |
郭志鹏, 李娟, 赵友刚, 等. 物联网中的无线传感器网络技术综述[J]. 计算机与应用化学, 2019, 36(1): 72-83. Doi:10.16866/j.com.app.chem201901009 |
| [3] |
Handy M J, Haase M, Timmermann D. Low energy adaptive clustering hierarchy with deterministic cluster-head selection[C]//4th International Workshop on Mobile and Wireless Communications Network. September 9-11, 2002, Stockholm, Sweden. IEEE, 2002: 368-372. DOI: 10.1109/MWCN.2002.1045790.
|
| [4] |
Tripathi M, Gaur M S, Laxmi V, et al. Energy efficient LEACH-C protocol for wireless sensor network[C]//Third International Conference on Computational Intelligence and Information Technology (CⅡT 2013). October 18-19, 2013, Mumbai. IET, 2013: 402-405. DOI: 10.1049/cp.2013.2620.
|
| [5] |
Janson S, Luczak T, Rucinski A. Random graphs[M]. Hoboken, NJ, USA: John Wiley & Sons, Inc., 2000. Doi:10.1002/9781118032718
|
| [6] |
董发志, 丁洪伟, 杨志军, 等. 基于遗传算法和模糊C均值聚类的WSN分簇路由算法[J]. 计算机应用, 2019, 39(8): 2359-2365. Doi:10.11772/j.issn.1001-9081.2019010134 |
| [7] |
武小年, 张楚芸, 张润莲, 等. WSN中基于改进粒子群优化算法的分簇路由协议[J]. 通信学报, 2019, 40(12): 114-123. Doi:10.11959/j.issn.1000?436x.2019241 |
| [8] |
凌春, 孙文胜. 基于改进蚁群算法的无线传感器网络路由[J]. 计算机工程与设计, 2019, 40(3): 627-631, 637. Doi:10.16208/j.issn1000-7024.2019.03.006 |
| [9] |
胡春安, 叶健. 基于鲸鱼算法的无线传感器网络分簇路由算法[J]. 计算机工程与设计, 2019, 40(11): 3067-3072. Doi:10.16208/j.issn1000-7024.2019.11.002 |
| [10] |
Dan S. Biogeography-based optimization[J]. IEEE Transactions on Evolutionary Computation, 2008, 12(6): 702-713. Doi:10.1109/TEVC.2008.919004 |
| [11] |
Guo W A, Chen M, Wang L, et al. A survey of biogeography-based optimization[J]. Neural Computing and Applications, 2017, 28(8): 1909-1926. Doi:10.1007/s00521-016-2179-x |
| [12] |
Jain A K. Data clustering: 50 years beyond K-means[J]. Pattern Recognition Letters, 2010, 31(8): 651-666. Doi:10.1016/j.patrec.2009.09.011 |
| [13] |
Holland J H. Genetic algorithms[J]. Scientific American, 1992, 267(1): 66-73. Doi:10.1038/scientificamerican0792-66 |
| [14] |
Yuan X H, Elhoseny M, El-Minir H K, et al. A genetic algorithm-based, dynamic clustering method towards improved WSN longevity[J]. Journal of Network and Systems Management, 2017, 25(1): 21-46. Doi:10.1007/s10922-016-9379-7 |
| [15] |
Bhushan S, Pal R, Antoshchuk S G. Energy efficient clustering protocol for heterogeneous wireless sensor network: a hybrid approach using GA and K-means[C]//2018 IEEE Second International Conference on Data Stream Mining & Processing. August 21-25, 2018, Lviv, Ukraine. IEEE, 2018: 381-385. DOI: 10.1109/DSMP.2018.8478538.
|
 2024, Vol. 41
2024, Vol. 41 


