2. 中国科学院大学电子电气与通信工程学院, 北京 100049;
3. 北京理工雷科电子信息技术有限公司, 北京 100081
2. School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 100049, China;
3. Beijing Racobit Electronic Information Technology Co. Ltd, Beijing 100081, China
合成孔径雷达(synthetic aperture radar, SAR)是一种主动式微波遥感成像雷达,与光学成像系统相比,它具有全天时全天候和分辨率不随观测距离变化等优点[1]。干涉合成孔径雷达(interferometic SAR, InSAR)是利用SAR,以单轨或重轨的方式进行观测,通过对同一地区的2次成像数据进行干涉处理得到该地区的形变和高程等信息[2],其中,差分干涉(differential InSAR, DInSAR)是以重轨方式获取形变信息的干涉技术[3]。
近年来,小型无人机变得越来越普遍,在军事领域和民用领域都得到广泛应用[4],无人机SAR的研究越来越受到国内外专家学者的重视。无人机DInSAR在技术和经济上的优势很明显: 第一,无人机DInSAR容易获得高空间分辨率和高密度覆盖的地壳形变场[5]; 第二,无人机的飞行轨道可灵活定制,从而有效弥补星载SAR因轨道固定只能观测视线方向形变的不足。2019年,瑞士的GAMMA公司进行了世界上首次无人机DInSAR试验,工作于L波段[6],获得了质量良好的差分干涉相位图。此外,早在2012年,巴西坎皮纳斯州立大学(UNICAMP)的研究者就提出无人机多波段多功能InSAR的概念[7];直到2019年,他们成功研制首个多波段多功能无人机DInSAR系统[8];2020年,他们在UNICAMP试验场进行了首次飞行试验,通过角反射器模拟形变的方式,得到形变测量的标准差为7.4 mm[8]。
在DInSAR处理中,基线是一个至关重要的参数。基线定义为照射同一区域的2个天线之间的相位中心距离。稳定的干涉基线是DInSAR测量的基础,基线的精度直接关系到反演高程和形变测量的精度。因此,研究有效的基线估计方法具有重要意义。目前,世界上本领域的学者们已提出过多种基线估计的算法,主要可分为3类:基于运动传感器测量数据、干涉定标以及基于回波干涉相位傅里叶变换[9]。运动传感器测量数据法的基本思想是利用干涉基线与轨道参数之间的几何关系,通过运动传感器数据得到轨道参数,然后根据几何关系解算基线值。干涉定标法的基本思想是利用已知高程信息和若干地面控制点信息,结合干涉几何关系,获得高精度的基线参数。靳国旺等[10]针对覆盖面积较大的多套InSAR数据,提出一种基于相位偏移的区域网平差基线估计算法,以减少地面控制点的数量和不同数据的高程差异。Xiong等[11]针对区域网平差方法中需要提取重叠区域连接点以及地面控制点存在误差的缺点,建立地面控制点和重叠区域连接点的误差方程,通过迭代算法计算基线参数。干涉相位傅里叶变换法1997年由Singh等[12]首次提出,它的基本思想是通过对一定范围内的干涉复图像进行傅里叶变换,得到干涉条纹的频率范围值,然后用条纹频率与基线的关系代入求解基线参数。后来的学者们提出了一些改进算法:唐晓青等[13]提出通过提高频谱分辨率和选择合适的窗口大小提高干涉条纹精度的方法;徐华平等[14]提出采用半牛顿迭代法和曲线拟合法提高干涉条纹频率精度;Wang等[15]提出采用最小二乘法在基线估计中利用较多的干涉条纹频率,从而提高干涉条纹频率准确性的方法。
上述的3类基线估计方法,主要是针对星载InSAR平台提出的,在无人机DInSAR上应用存在不同的问题。第一,星载SAR的轨道很稳定,所以运动传感器测量的轨道参数精度很高。但是在无人机平台上,首先,无人机飞行受气流扰动影响较大,所以无人机重轨测量2次的飞行轨迹,难以保证重合性[16];其次,无人机重量较轻,其载荷重量限制要求较高,往往无法搭载高精度POS,低精度POS所得到的轨道参数并不准确[8]。这导致在现有的低精度POS系统条件下,无人机DInSAR基线估计存在困难。第二,干涉定标法严重依赖于控制点的精度,但是在某些特殊地形区域,控制点测量较为困难。并且,定标法需要较多的控制点数量[9],当应用无人机进行快速应急检测时,对于无人机差分干涉来说,往往无法实现。第三,干涉相位傅里叶变换法需要连续的质量较好的干涉相位,星载SAR的幅宽很宽,并且轨道稳定,容易找到连续的质量较好的干涉相位。但是无人机轨道不稳定并且重轨干涉时间去相关较为严重,所以干涉相位质量受噪声影响较大,这种情况下,干涉相位傅里叶变换法会精度不高甚至失效[9]。2005年,裴怀宁等[17]提出基于干涉相位周期进行基线估计的方法,其绝对误差达到毫米级,但是该方法仅选取了3个点位数据进行基线估计,并未利用干涉相位的全部有效信息,这样基线估计的结果受噪声的影响较大,鲁棒性不足。
综上所述,无人机因其重量和体积的限制,易受气流扰动影响导致运动误差增大,并且往往无法搭载高精度POS,受到低精度POS的限制,得到的轨道参数不准确。此外,无人机因其机动灵活成本可控的特点,在快速应急检测和特殊地形的场景中应用广泛,但是在快速应急检测和特殊地形应用场景中,定标较为困难,往往无法实现。上述特点使得传统的3类基线估计方法在无人机平台上应用均存在一定局限性。因此,本文提出改进的基于干涉相位周期的基线估计方法。其基本思路是,在干涉相位图上选择2π相位周期循环的若干点位,通过干涉几何关系可推导出干涉相位周期、斜距、2点之间距离、相位差的关系,代入已知参数,采用最小二乘法即可解算出基线值。这样,就利用了更多的干涉相位的有效信息,减小了噪声的影响。
1 干涉相位周期模型分析基于干涉相位周期进行基线估计的方法基本思路是,在测绘区内选取一块平地区域,在干涉相位图上取相位差刚好为第1个2π循环的2点,在雷达图像上通过像素距离、像素数计算出2点之间距离,通过干涉几何关系推导出干涉相位周期、斜距、2点之间距离、相位差的关系,代入已知参数即可解算出基线值。本节简要介绍推导过程。
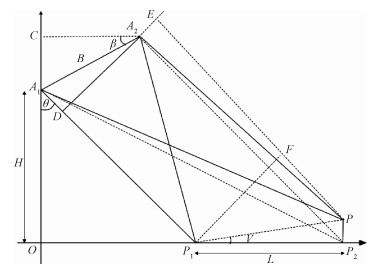
以干涉相位周期进行基线估计的几何关系如图 1所示。
|
Download:
|
| 图 1 干涉几何关系 Fig. 1 InSAR geometry | |
如图所示,A1、A2为2轨飞行的天线相位中心,P1、P2为地面上2点,除图上标注的参数外,设定如下参数及几何关系,并可得下列表达式:
| $\begin{gathered} A_1 P_1=R, A_2 P_1=R_1, A_1 P_2=R_2, A_2 P_2=R_3 , \\ A_1 D=B_{\|}, A_2 D=B_{\perp}, P_1 F=a, \\ P_2 F=b, P_1 P_2=L, A_1 P_1 \perp D E, E P \perp F P_1 \\ B_{\perp}=B \cos (\theta-\beta), \end{gathered}$ | (1) |
| $a=\frac{L}{\cos \gamma} \cos (\theta-\gamma) \text {, }$ | (2) |
| $R_1=\sqrt{\left(R-B_{\|}\right)^2+B_{\perp}^2} \approx R+\frac{B_{\perp}^2}{2 R}, $ | (3) |
| $R_2=\sqrt{(R+b)^2+a^2} \approx R+\frac{a^2}{2 R}, $ | (4) |
| $\begin{gathered} R_3=\sqrt{\left(R-B_{\|}+b\right)^2+\left(a-B_{\perp}\right)^2} \approx \\ R+\frac{\left(a-B_{\perp}\right)^2}{2 R} . \end{gathered}$ | (5) |
根据上述表达式,经过推导和化简可得P1和P2点干涉相位差为
| $\Delta \varphi=\Delta \varphi_1-\Delta \varphi_2=\frac{4 {\rm{ \mathsf{ π} }} a B_{\perp}}{\lambda R}.$ | (6) |
令ρ为像素距离,N为2点之间的像素差,则P1、P2 2点之间的距离L为
| $L=\rho N.$ | (7) |
把式(1)、式(2)和式(7)代入式(6),可得
| $\begin{gathered} \Delta \varphi=\frac{4 {\rm{ \mathsf{ π} }}}{\lambda} \times \\ \frac{B^2 \rho N \cos (\theta-\beta) \cos (\theta) \cos (\theta-\gamma)}{H \cos \gamma}. \end{gathered}$ | (8) |
当Δφ=2π,代入到式(8)中,化简后可得
| $\begin{gathered} (B \cos \theta \cos \beta+B \sin \theta \sin \beta) \times \\ \left(\cos ^2 \theta+\sin \theta \cos \theta \tan \gamma\right)=\frac{\lambda H}{2 \rho N}. \end{gathered}$ | (9) |
即只要知道波长、下视角、飞行高度等系统参数,即可解算出基线值。
根据本节的推导过程可知,此方法的优点是与轨道参数无关,只需知道干涉相位周期、系统参数以及从图像上算出特定2点的距离即可。但在文献[17]中,仅选取了3个点位数据进行基线估计;然而,在实际应用中,由于干涉SAR基线的时空去相关、热噪声等因素的影响,不可避免地会产生系统噪声。如果只使用3个点位数据进行基线估计,很难有效地抑制相位噪声,而且在低信噪比区域增加的相位周期误差会导致基线参数估计误差变大。因此,现有方法的鲁棒性有待提高。为抑制噪声,我们选取同一方位上多个距离像元的有效干涉相位数据,并通过最小二乘法提高基线估计的精度。
假设选取n组同一方位上的距离像元的有效干涉相位数据,那么,根据本节推导,各组数据与基线参数之间满足方程:
| $\begin{gathered} B_x\left(\sin \theta_1 \cos ^2 \theta_1+\sin ^2 \theta_1 \cos \theta_1 \tan \gamma\right)+ \\ B_y\left(\cos ^3 \theta_1+\sin \theta_1 \cos ^2 \theta_1 \tan \gamma\right)= \\ \frac{\lambda H}{2 \rho N_1}, \\ B_x\left(\sin \theta_2 \cos ^2 \theta_2+\sin ^2 \theta_2 \cos \theta_2 \tan \gamma\right)+ \\ B_y\left(\cos ^3 \theta_2+\sin \theta_2 \cos ^2 \theta_2 \tan \gamma\right)= \\ \frac{\lambda H}{2 \rho N_2}, \\ \cdots \cdots \\ B_x\left(\sin \theta_n \cos ^2 \theta_n+\sin ^2 \theta_n \cos \theta_n \tan \gamma\right)+ \\ B_y\left(\cos ^3 \theta_n+\sin _n \cos ^2 \theta_n \tan \gamma\right)= \\ \frac{\lambda H}{2 \rho N_n} . \end{gathered}$ | (10) |
把式(10)改写为矩阵表达式:
| $\boldsymbol{U} \boldsymbol{X}=\boldsymbol{V}, $ | (11) |
| $\begin{gathered} \boldsymbol{U}=\left(\begin{array}{cc} u_{11} & u_{12} \\ u_{21} & u_{22} \\ \vdots & \vdots \\ u_{n 1} & u_{n 2} \end{array}\right), \\ \boldsymbol{X}=\left(\begin{array}{l} B_x \\ B_y \end{array}\right), \\ \boldsymbol{V}=\left(\begin{array}{c} \frac{\lambda H}{2 \rho N_1} \\ \frac{\lambda H}{2 \rho N_2} \\ \vdots \\ \frac{\lambda H}{2 \rho N_n} \end{array}\right), \end{gathered}$ | (12) |
| $u_{i 1}=\sin \theta_i \cos ^2 \theta_i+\sin ^2 \theta_i \cos \theta_i \tan \gamma, $ | (13) |
| $\begin{gathered} u_{i 2}=\cos ^3 \theta_i+\sin \theta_i \cos ^2 \theta_i \tan \gamma, \\ i=1, 2, \cdots, n . \end{gathered}$ | (14) |
其中:ui1和ui2是与下视角θi有关的系数,Ni代表选择的同一方位上2个距离像元之间的像素差。因此,根据最小二乘理论,基线参数可根据解下式得到
| $\min\limits_{x \in \mathbf{R}^n}\|\boldsymbol{U} \boldsymbol{X}-\boldsymbol{V}\|_2^2$ | (15) |
根据矩阵理论,式(15)中X的解的表达式为
| $\boldsymbol{X}=\left(\boldsymbol{U}^{\mathrm{T}} \boldsymbol{U}\right)^{-1} \boldsymbol{U}^{\mathrm{T}} \boldsymbol{V}.$ | (16) |
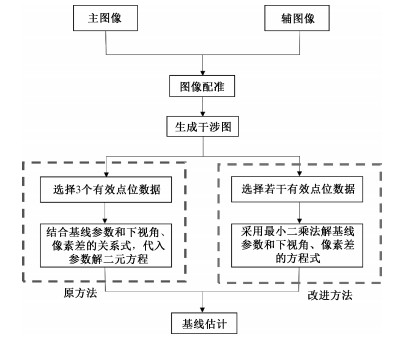
综上所述,本文提出的改进方法与原方法的对比如图 2所示。
|
Download:
|
| 图 2 原方法与改进方法的流程图对比 Fig. 2 Comparison of the flow chart of the original method and the improved method | |
针对无人机的运动误差大、因重量和体积小受低精度POS的限制、在快速应急检测的应用场景中往往无法实现定标导致传统的3类基线估计方法不适用于无人机平台的问题,本文提出改进的基于干涉相位周期的基线估计方法。其理论推导是基于平地地形的。而InSAR应用在高程反演、形变测量时,一般不会是平地地形,在这种情况下想应用此方法,就要在测绘带内选择一块平坦地区的干涉相位。而这一点是不难实现的,平地区域可以根据小比例尺的地形图和雷达图像的强度图进行选取[18]。在进行重轨航线设计时,就要根据实际地形选择一块平坦地形测绘带,那么选择合适的平坦地形测绘带幅宽以获得足够数量的干涉条纹就很重要。本节推导干涉条纹数量与平地测绘带幅宽和系统参数的关系。
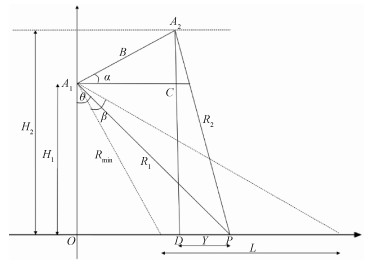
为方便表述,画出求平地相位的几何关系图如图 3所示。
|
Download:
|
| 图 3 平地相位几何关系 Fig. 3 Flat-earth phase geometry | |
如图所示,A1和A2为2轨的天线相位中心,H1和H2分别为2轨的飞行高度,R1和R2为2轨天线相位中心到地面点P的斜距,θ为中心下视角,β为波束宽度,Rmin为近斜距,L为幅宽,Rbin为像素距离,N为距离向采样点数,φ为干涉相位,根据几何关系可得
| $\varphi=-\frac{4 {\rm{ \mathsf{ π} }}\left(R_1-R_2\right)}{\lambda}, $ | (17) |
| $R_1=R_{\min }+(N-1) R_{\text {bin }}, $ | (18) |
| $N=\frac{L}{R_{\text {bin }}} \text {, }$ | (19) |
| $R_2=\sqrt{H_2^2+Y^2}, $ | (20) |
| $Y=\sqrt{R_1^2-H_1^2}-B \cos \alpha, $ | (21) |
| $H_2=H_1+B \sin \alpha .$ | (22) |
因为当干涉相位每经过一次2π循环,就形成一个干涉条纹,假设干涉条纹数量为n,则有
| $R_1-R_2=\left[-\frac{\lambda}{2}, -\lambda, \cdots \cdots, -\frac{\lambda}{2} n\right]^{\mathrm{T}} .$ | (23) |
将式(17)~式(22)代入到式(23)中,并结合波束宽度和中心下视角,可得
| $R_{\min }+\left(\frac{L}{R_{\text {bin }}}-1\right) \frac{c}{2 B_{\mathrm{w}}}-\sqrt{\left(H_1+B \sin \alpha\right)^2+\left(\sqrt{\left[R_{\min }+\left(\frac{L}{R_{\text {bin }}}-1\right) \frac{c}{2 B_{\mathrm{w}}}\right]^2-H_1^2}-B \cos \alpha\right)^2}, $ | (24) |
| $R_{\min }=\frac{H_1}{\cos \left(\theta-\frac{\beta}{2}\right)}, $ | (25) |
| $L=H_1\left[\tan \left(\theta+\frac{\beta}{2}\right)-\tan \left(\theta-\frac{\beta}{2}\right)\right] .$ | (26) |
结合式(24)~式(26),可求得获取干涉条纹数量n所对应的幅宽L。比如,根据表 1的仿真参数,如果想获得7条干涉条纹,那么所需的幅宽至少为276 m。
|
|
表 1 仿真参数 Table 1 Simulation parameters |
为验证本文所提出的改进的基线估计方法,在表 1中模拟了无人机平台的系统参数。首先基于平地模型模拟对应的主、辅图像;然后通过配准和干涉处理得到干涉条纹图,画出某一方位上距离向干涉相位曲线用于标志点选取;最后,利用原方法和改进的方法对基线参数进行估计,比较二者的结果。
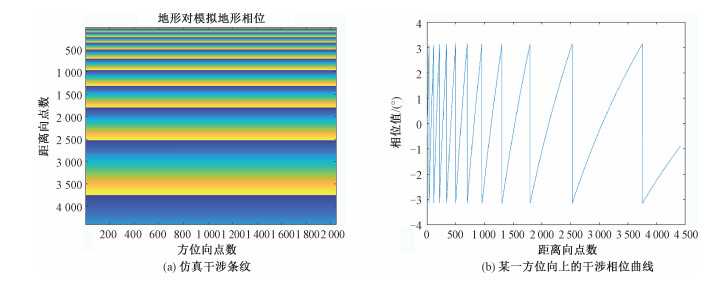
图 4(a)为仿真生成的干涉条纹图,可以看出从近距到远距,干涉条纹的密度从密集到稀疏;图 4(b)为某一方位向上的沿距离向的干涉相位曲线。
|
Download:
|
| 图 4 仿真结果 Fig. 4 Simulated results | |
为验证本文提出的改进方法的有效性和鲁棒性,利用原方法与改进方法对同一干涉条纹图进行基线估计,并对2种基线估计方法的试验结果进行分析和比较。
图 5展示原方法与改进方法的基线估计绝对误差比较,对2种方法分别选取多组数据进行基线估计。图 5(a)为原方法的基线估计绝对误差,图 5(b)为改进方法的绝对误差。通过比较2种方法的基线估计绝对误差的柱状图结果,可以直观地看出,改进方法的绝对误差要比原方法小。
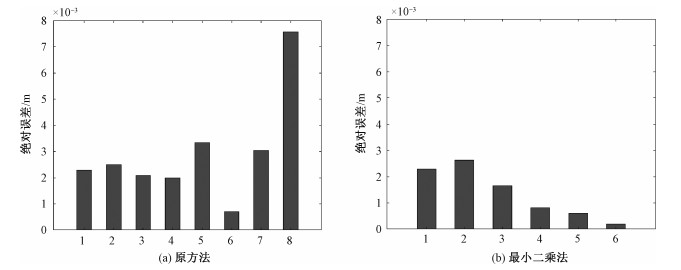
|
Download:
|
| 图 5 2种方法基线估计绝对误差的仿真结果 Fig. 5 Simulation results on the absolute error of baseline estimation by two methods | |
为进一步说明原方法和改进方法的基线参数估计精度,计算2种方法的均方根误差(root mean squared error,RMSE)和标准差,并对其进行比较。表 2列出2种方法的RMSE和标准差的计算结果。
|
|
表 2 2种方法的RMSE和标准差的仿真结果 Table 2 Simulation results on RMSE and standard deviation by two methods |
从表 2可看出,改进方法的基线估计精度相比于原方法有明显提升。改进方法的RMSE相对原方法降低53.4%;改进方法的标准差相比于原方法降低65.5%。也就是说,改进方法大幅提高了原方法的鲁棒性。
为说明改进方法中所取的数据量n与误差性能的关系,计算了不同的数据量n对应的RMSE以及运行时间,结果如表 3所示。
|
|
表 3 数据量n与RMSE和运行时间的关系 Table 3 Data volume n versus RMSE and runtime |
从表 3可看出,随着数据量的增加,RMSE呈逐渐减小的趋势, 数据量7与数据量3相比,运行时间仅增加不到1 s。
综上所述,通过仿真结果分析可以得出结论:与原方法相比,本文提出的改进方法具有明显的优势,基线估计的绝对误差和相对误差都降低了,其精度和鲁棒性都得到了显著提高。
3.2 飞行试验结果分析为验证改进方法对实际数据处理的效果,对无人机双天线DInSAR的飞行数据进行了处理。试验所用飞行数据为2020年10—11月获取的,采用正侧视成像。试验所用Ku波段微型SAR系统为中国科学院空天信息创新研究院研制的,系统组成包括机上设备和地面设备。机上设备包括微型SAR主机、收发天线(包括1发2收3幅轻小型微带天线,以交轨方式安装)、小型化POS(包括PCS、GPS天线、IMU等模块,其中PCS模块集成在Ku波段微型SAR主机中)等部分;地面设备包括SAR地面控制单元、差分GPS基站、地面控制和处理单元等部分。本次试验一共进行了4个条带的飞行,其中单轨飞行的双天线数据可用来获取高程信息,重轨飞行可用来获取形变信息。测绘区地形平整,飞行和成像基本参数如表 4所示。
|
|
表 4 微型SAR飞行参数 Table 4 Mini-SAR flight parameters |
在试验场进行了双天线交轨干涉以及重轨干涉的飞行试验。图 6(a)为无人机和微型SAR系统,6(b)为飞行试验现场,6(c)为主图像的成像结果。

|
Download:
|
| 图 6 微型SAR飞行试验 Fig. 6 Mini-SAR flight test | |
为说明本方法的基线估计效果,使用原方法和改进方法分别对2种干涉模式进行基线估计。
在双天线干涉模式下,因为2个天线的运动是时空同步的,所以二者的相位中心在一个坐标系下。基线则可根据天线相位中心坐标直接计算,根据POS解算出的天线相位中心计算得到基线长度为0.122 9 m,以此作为基线估计的参考值。与上文类似,图 7展示了原方法与改进方法的基线估计绝对误差比较,对2种方法分别选取多组数据进行基线估计。图 7(a)为原方法的基线估计绝对误差,7(b)为改进方法的绝对误差。通过比较柱状图结果,可以直观地看出,改进方法的绝对误差要比原方法小,原方法的基线估计绝对误差为厘米级,改进方法的基线估计绝对误差达到毫米级。
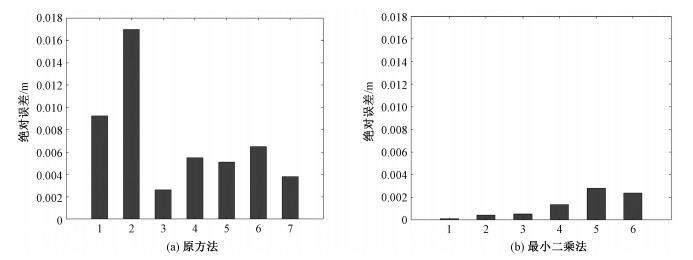
|
Download:
|
| 图 7 2种方法基线估计绝对误差的试验结果 Fig. 7 Experiment results on the absolute error of baseline estimation by two methods | |
为进一步验证本文提出的改进方法的有效性,同时采用原方法和改进方法进行多次基线估计,并对2种方法的均方根误差和标准差进行比较。表 5列出2种方法的RMSE和标准差的计算结果。
|
|
表 5 2种方法的RMSE和标准差的试验结果 Table 5 Experiment results on RMSE and standard deviation by two methods |
从表 5可以看出,改进方法的RMSE相对原方法降低74.5%,标准差相比于原方法降低80.4%,即改进方法显著提高了基线估计的精度和鲁棒性。
在重轨干涉模式下,与双天线干涉不同的是,2次重轨飞行轨迹并不在一个坐标系下,所以2次重轨飞行的残余运动误差无法相互抵消。由于残余运动误差的存在,使得想要通过运动传感器测量法获得一个相对准确的基线参考值是较为困难的。所以我们分别以基于原方法的基线估计和改进方法的基线估计结果进行去平地处理,并对基于2种方法得到的去平地相位进行比较。图 8展示了去平地相位结果。

|
Download:
|
| 图 8 去平地相位结果 Fig. 8 Phase flattening results | |
在GOOGLE EARTH上查看测绘区域,发现测区的海拔高度基本是一致的,经过现场实地测量,确认测区大致为平地,所以理论上去平地后的地形相位应大致一致。图 8(a)为基于原方法的基线估计结果得到的去平地相位,可看出地形相位从近距到远距有明显的变化,所以地形有一个明显的倾斜角度。图 8(b)为基于改进方法的基线估计结果得到的去平地相位,可看出其地形相位是趋于一致的,说明地形大致是平地。由此可以推论,图 8(a)地形倾斜的原因是由于基线估计不准确导致的,改进方法的基线估计结果要更为准确。
综上所述,对比基于原方法和改进方法对双天线干涉和重轨干涉的实际飞行数据的数据处理结果,改进方法的基线估计精度和鲁棒性相比原方法有了显著提高。
4 结论本文从无人机的特点和应用场景出发,针对传统的3类基线估计方法不适用于无人机平台的问题,提出一种改进的基于干涉相位周期进行无人机双天线DInSAR基线估计的方法。通过在测绘区内选取一块平地区域,结合SAR图像和干涉几何关系推导出基线与飞行参数的关系式,选取多组数据采用最小二乘法解算出基线值。此外还针对本方法需要一定面积的平地相位的问题,给出干涉条纹数量与测绘幅宽的关系式。仿真及试验结果表明,改进方法获取的基线估计精度和鲁棒性比原方法有显著提高。本文为无人机双天线DInSAR快速应急监测的应用场景提供了基线估计的新思路。下一步,将结合具体应用场景,增加控制点研究进一步提高无人机双天线DInSAR基线估计精度的方法。
| [1] |
Mastro P, Serio C, Masiello G, et al. The multiple aperture SAR interferometry (MAI) technique for the detection of large ground displacement dynamics: an overview[J]. Remote Sensing, 2020, 12(7): 1189. Doi:10.3390/rs12071189 |
| [2] |
林世明, 张毅, 王吉利, 等. 星载双基InSAR系统中的电离层色散效应分析与校正[J]. 中国科学院大学学报, 2021, 38(6): 809-816. Doi:10.7523/j.issn.2095-6134.2021.06.011 |
| [3] |
Hu B, Li H, Zhang X F, et al. Oil and gas mining deformation monitoring and assessments of disaster: using interferometric synthetic aperture radar technology[J]. IEEE Geoscience and Remote Sensing Magazine, 2020, 8(2): 108-134. Doi:10.1109/MGRS.2020.2989239 |
| [4] |
马娇, 董勇伟, 李原, 等. 多旋翼无人机微多普勒特性分析与特征提取[J]. 中国科学院大学学报, 2019, 36(2): 235-243. Doi:10.7523/j.issn.2095-6134.2019.02.011 |
| [5] |
Moreira L, Castro F, Góes J A, et al. A drone-borne multiband DInSAR: results and applications[C]//2019 IEEE Radar Conference (RadarConf). April 22-26, 2019, Boston, MA, USA. IEEE, 2019: 1-6. DOI: 10.1109/RADAR.2019.8835653.
|
| [6] |
Frey O, Werner C L, Coscione R. Car-borne and UAV-borne mobile mapping of surface displacements with a compact repeat-pass interferometric SAR system at L-band[C]//IGARSS 2019-2019 IEEE International Geoscience and Remote Sensing Symposium. July 28-August 2, 2019, Yokohama, Japan. IEEE, 2019: 274-277. DOI: 10.1109/IGARSS.2019.8897827.
|
| [7] |
Remy M A, de Macedo K A C, Moreira J R. The first UAV-based P- and X-band interferometric SAR system[C]//2012 IEEE International Geoscience and Remote Sensing Symposium. July 22-27, 2012, Munich, Germany. IEEE, 2012: 5041-5044. DOI: 10.1109/IGARSS.2012.6352478.
|
| [8] |
Luebeck D, Wimmer C, Moreira L F, et al. Drone-borne differential SAR interferometry[J]. Remote Sensing, 2020, 12(5): 778. Doi:10.3390/rs12050778 |
| [9] |
Lu H, Suo Z Y, Li Z F, et al. InSAR baseline estimation for Gaofen-3 real-time DEM generation[J]. Sensors(Basel, Switzerland), 2018, 18(7): 2152. Doi:10.3390/s18072152 |
| [10] |
靳国旺, 吴一戎, 向茂生, 等. 基于区域网平差的InSAR基线估计方法[J]. 测绘学报, 2011, 40(5): 616-622, 627. |
| [11] |
Xiong X, Jin G W, Zhang H M, et al. Baseline estimation with block adjustment considering ground control point errors for multi-pass dual-antenna airborne INSAR[C]//2016 IEEE International Geoscience and Remote Sensing Symposium. July 10-15, 2016, Beijing, China. IEEE, 2016: 6460-6463. DOI: 10.1109/IGARSS.2016.7730688.
|
| [12] |
Singh K, Stussi N, Keong K L, et al. Baseline estimation in interferometric SAR[C]//IGARSS'97.1997 IEEE International Geoscience and Remote Sensing Symposium Proceedings. Remote Sensing-A Scientific Vision for Sustainable Development. August 3-8, 1997, Singapore. IEEE, 1997: 454-456. DOI: 10.1109/IGARSS.1997.615913.
|
| [13] |
唐晓青, 向茂生, 吴一戎. 一种改进的基于干涉相位的基线估计方法[J]. 电子与信息学报, 2008, 30(12): 2795-2799. Doi:10.3724/SP.J.1146.2007.01974 |
| [14] |
徐华平, 朱玲凤, 刘向华, 等. 一种基于干涉条纹频率的星载InSAR基线估计新方法[J]. 电子学报, 2011, 39(9): 2212-2216, 封3. |
| [15] |
Wang Y, Xu H P, Li S, et al. An improved InSAR baseline estimation based on interferometric fringe frequency[C]//2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS. July 11-16, 2021, Brussels, Belgium. IEEE, 2021: 4296-4299. DOI: 10.1109/IGARSS47720.2021.9554863.
|
| [16] |
董小桐, 韩春明, 岳昔娟, 等. 一种机载重轨InSAR高精度三维定位方法[J]. 中国科学院大学学报, 2019, 36(6): 844-850. Doi:10.7523/j.issn.2095-6134.2019.06.017 |
| [17] |
裴怀宁, 马德宝, 郑芳. 基于平地干涉相位周期的基线估计方法[J]. 现代雷达, 2005, 27(11): 48-50. Doi:10.16592/j.cnki.1004-7859.2005.11.013 |
| [18] |
靳国旺, 徐青, 朱彩英, 等. 利用平地干涉相位进行INSAR初始基线估计[J]. 测绘科学技术学报, 2006, 23(4): 278-280, 283. Doi:10.3969/j.issn.1673-6338.2006.04.013 |
 2024, Vol. 41
2024, Vol. 41 


