2. 中国科学院苏州纳米技术与纳米仿生研究所, 江苏 苏州 215123
2. Suzhou Institute of Nano-tech and Nano-bionics, Chinese Academy of Sciences, Suzhou 215123, Jiangsu, China
硅PUF(silicon physical unclonable function)是指可以响应已有的二进制输入序列,获得一个与集成电路物理结构相关的独立二进制序列的基于硅基集成电路实现的PUF。输入PUF的二进制序列称为挑战,PUF输出的二进制序列称为响应,二者合称为PUF的挑战-响应对(challenge-response pairs, CRP)。通常使用片内汉明距离(intra-chip hamming distance)衡量PUF对于同一个挑战信号的可重现性,片间汉明距离(inter-chip hamming distance)衡量PUF之间的差异性。理想的PUF片内汉明距离为0,片间汉明距离是响应二进制序列长度的50%。相比于传统的efuse等OTP方案存储密钥的方式,硅PUF具有不可预测、不可克隆和即时生成等CRP特性,使得搭载PUF的芯片或终端在设备认证、密钥生成等过程中能够更有效地抵抗外部攻击[1-2]。
硅PUF具有多种实现方式。由于制造过程产生的微观不确定性,相同的电路单元在电路结构上存在微小差异。典型的硅PUF通过耦合具有竞争关系的微观差异性,使得竞争输出的数值具有芯片间随机的特性。基于电路延迟特性的硅PUF最为常见的类型是仲裁PUF[3-4]和环形振荡器PUF[5-6],通过仲裁器判定2个竞争信号抵达的先后顺序,获得PUF的响应。SRAM-PUF[7-8]、DRAM-PUF[9]和触发器PUF[10]等属于基于存储器的PUF。这些方式实现的PUF借助存储器的电路结构,产生了电压或者电流的竞争关系,作为直接获得的二进制响应数据。随着PUF技术受到的关注度逐渐提高,一些新类型的PUF也开始出现在芯片设计中,比如改进结构的SRAMPUF[11]和基于新型存储器的RRAM-PUF[12]等。
然而,基于竞争电路参数差异实现的PUF方案中,因为PUF阵列中一些竞争参数差异过小的电路单元,存在一定数量的不稳定位[13]。对于同一个挑战信号的反复请求,PUF很难做到100%的响应可重现性,极大限制了其在密钥生成、数据掩码生成等需要精确重复二进制序列的场景中的应用。对此,Dodis等[14]在2004年提出一种模糊提取器(fuzzy extractor)方案有效解决了这一问题。模糊提取器早期应用于从噪声随机源中提取均匀且稳定的随机字符串,后来被逐步引入指纹、虹膜、人脸识别等生物信息识别的场景中[15-17],也可以用于还原PUF的不稳定位[18]。另一方面,模糊提取器被证明对被动攻击者具有较好的抵御作用[19-20],可以保障其与PUF结合的整体安全性。模糊提取器还原数据的核心算法是基于纠错码(error correction code, ECC)完成的。BCH码(Bose-Chaudhuri-Hocquenghem Codes)是线性分组码中循环码的子类,能够纠正码字中的多位错误,实现精确译码[21]。BCH码可以对二进制码进行纠错,便于在计算机系统中实现,常用于中短码通信编码和Flash存储等场景。因此,PUF的模糊提取方案中也经常借助BCH码精确译码、多位还原、长度可选择的特性进行实现。
在完成相关RTL(register transfer level)设计后,通常需要对其进行功能验证。通用验证方法学(universal verification methodology, UVM)是一种以SystemVerilog语言为工具的验证平台开发方法学,其功能特色是具有可重用的组件,搭建的验证环境具有标准化的层次结构和接口,更适合于大规模验证[22]。
课题组的前期工作[23]测试了华虹宏力0.11 μm CMOS平台SRAM PUF不稳定度约为20%,需要搭载大容量的纠错码后处理算法保持PUF的可重现性。本文参考了前期工作和类似结构的文献[24-26]中的测试结果,设计并验证了一种面向PUF的大纠错容量模糊提取器。该设计使用最大值冒泡算法,优化了BCH码译码算法中Berlekamp-Massey(BM)算法临时数据存储开销过大的问题,通过对数/反对数表的方案完成BCH码中的指数计算,可以实现约21.25%的纠错容量。该芯片在华虹宏力0.11 μm CMOS工艺下制造。测试结果表明,该模糊提取器可以实现预期纠错能力,维持稳定的PUF挑战响应功能。
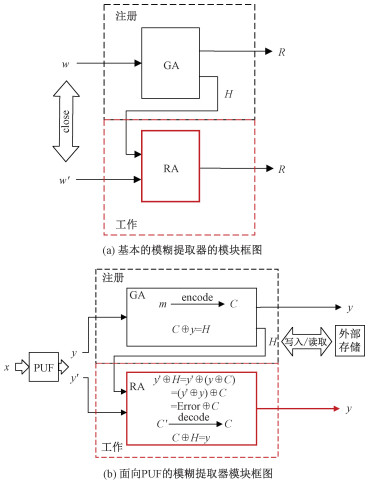
1 算法原理 1.1 模糊提取器模糊提取器(fuzzy extractor, FE)主要包含生成算法(generation algorithm, GA)和再生算法(regeneration algorithm, RA)2个部分,在使用的时候需要经历注册和工作2个阶段。如图 1所示,在注册阶段,FE读取初始二进制序列w输入GA,获得输出数据R和帮助文件H;在工作阶段,FE仍然从数据源读取二进制序列,读出的数据相比注册阶段的数据可能出现误差,记为w′,将w′和H输入RA,可以获得输出R′。当w和w′的距离足够接近的时候,R=R′,从而在工作阶段实现数据的再生。模糊提取器在密钥协商、对称密钥生成等场景中均有应用。图 1(b)展示了面向硅PUF的模糊提取器模块示意图。在注册阶段,外部输入挑战信号x到PUF模块中,模糊提取器由此获得PUF的响应信号y进行GA计算,产生帮助文件H在其外部保存;当芯片复位或重新上电以后,PUF模块可能会产生少量数据的翻转,这时重新输入x获取相同位置的PUF响应y′,同时向RA中导入帮助文件H进行计算,可以将这部分PUF数据还原回初始的数值y。在GA计算时,借助熵源中的部分随机数据m,纠错码通过编码计算会生成和PUF响应信号y相等长度的数据C,模糊提取器将C和y进行模2加法计算,其结果为帮助文件H;在RA计算时,y′和H模2加计算的结果为包含有一定数量错误的C′,由纠错码的计算可以还原回C,再和H重新模2加,获得原始响应y。
|
Download:
|
| 图 1 模糊提取器的原理框图 Fig. 1 Schematic diagram of fuzzy extractor | |
1959年Hocquenghem、1960年Boss和Ray-Chaudhuri分别提出能够纠正码字中多个随机错误的循环码,这种纠错码一般以3人名字的首字母合称为BCH码。二进制BCH码的码字长度通常用n表示,其中包含k bit的信息位和(n-k) bit的校验位;纠错的位数用t表示;码字之间的汉明距离用d表示。
参考团队此前工作中对于SRAM阵列不稳定位的测试结果和类似结构的测试文献,我们选用了本源BCH码并配置其参数为(n, k, t)=(127, 15, 27),即在信息位为15 bit的时候,通过增加冗余到码字长度127 bit,可以纠正全码字中最多27 bit的错误。如1.1所述,BCH码同样包含编码和译码2个算法,其中编码计算可以由下式描述:
| $ c(x)=m(x) \cdot x^{n-k}+m(x) \cdot x^{n-k} \bmod g(x) \text {. } $ | (1) |
其中:c(x)是以多项式的形式表示纠错码的码字;m(x)在模糊提取器中是来源于熵源的随机二进制序列,简称信息位;g(x)是BCH码的生成多项式;x的乘积表示二进制序列的移位操作。
对于二进制序列,BCH译码算法主要包含3个步骤:计算伴随式S(x);计算错误位置多项式σ(x);求解σ(x)获得错误位置并纠正。在工作模式中重新获得c′(x)后,需要对其伴随式S(x)进行求解,将生成多项式的根αi代入接收多项式中进行计算:
| $ \begin{gathered} S_i=\sum\limits_{j=0}^{n-1} r_j\left(\alpha^i\right)^j=r_0\left(\alpha^i\right)^0+r_1\left(\alpha^i\right)^1+\cdots+ \\ r_1\left(\alpha^i\right)^{n-1}=\left(\cdots \left(\left(\left(r_{n-1}\left(\alpha^i\right)+r_{n-2}\right) \alpha^i+\right.\right.\right. \\ \left.\left.r_{n-3}\right) \alpha^i+\cdots+r_1\right) \alpha^i+r_0 . \end{gathered} $ | (2) |
其中:rj表示c′(x)多项式系数,α表示二元扩展域本原多项式的根。第2个等号后面的合并计算称为Homer迭代,是一种适合硬件电路迭代计算的公式变形。当所有的伴随多项式均为0时,说明响应信号y′相比注册时的y没有发生变化,若存在非0的伴随多项式,则需要进行第2步译码计算。
第2步计算中最常用的是BM算法。这是一种有限次迭代的算法,其算法步骤如图 2所示,最终计算出错误位置多项式σ(x)。每次迭代需要计算关键方程的差值d,当d为0时直接进入下一轮迭代判定,d不为0时需要将其代入迭代中进行计算。

|
Download:
|
| 图 2 BM算法流程图 Fig. 2 Flow chart of BM algorithm | |
BM算法的L(i)表示在第i次迭代过程中d的阶数。在获得完整的σ(x)后,需要逐位代入c′(x)的多项式系数求解σ(x)的根,这种算法由工程师钱天闻最早提出,故称为钱搜索算法。当c(x)的第n-l位存在错误的时候,代入σ(x)满足
| $ 1+\sigma_1 \alpha^l+\sigma_2 \alpha^{2 l}+\cdots+\sigma_t \alpha^{t l}=0 $ | (3) |
此时对该位的二进制数据进行翻转。当c′(x)所有的位都完成上述计算以后,BCH算法完成,得到c(x),经过第2次和帮助文件H(x)模2加后得到PUF的注册响应数据y。
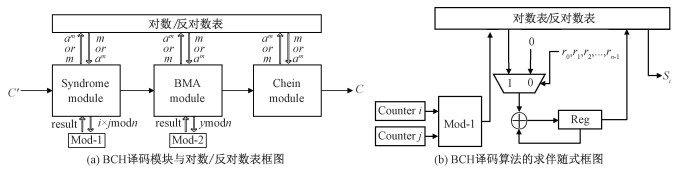
2 大纠错容量模糊提取器的实现 2.1 对数/反对数表模块在上述方程(1)~(3)中,主要的计算为加法和乘法,在BM算法的迭代计算中有一处除法运算。对于(127, 15, 27)BCH码来说,上述计算均为GF(27)有限域的计算。对于加法而言,计算过程和布尔计算的异或逻辑等效,容易在RTL设计中实现;对于有限域乘法和除法,经典的NAND flash译码器需要根据BCH码的本原多项式,设计专用的有限域乘法器和不进行求逆运算的iBM算法实现[26],这些处理方法会在伴随式求解、BM算法迭代和钱搜索求和中使用。当BCH码纠错容量较大时,需要更多数量的乘法器,显著增加了伴随式S(x)和BM算法所使用的硬件资源。为解决这一问题,需要将有限域计算转换到实数域进行处理。α作为本原多项式的根,α及其高次幂构成了有限域中的所有元素。其中α、幂指数(十进制)和α对应的向量(二进制)对照表如表 1所示。向量和幂指数的一一对应关系称为对数/反对数表。在BCH的译码器计算过程中涉及有限域乘除法的时候,但对于大纠错容量的BCH码而言,由于PUF在实际使用时上位机或系统的挑战请求少,不需要模糊提取器做流水线处理,因此可以设计对数/反对数表模块在上述3个译码计算模块之间共享而不会产生冲突。
|
|
表 1 (127, 15, 27)的BCH码对数/反对数表 Table 1 (127, 15, 27) BCH code logarithm/opposition table |
如图 3(a)所示,将乘数αm发送到对数表/反对数表模块中进行处理,其后返回一个可以在实数域中计算的幂指数m,将返回的数值进行实数域计算(m+m=2m),再将计算后的数值送入mod模块求余数(p=2m mod n),将返回值(result=p)重新输入对数表/反对数表模块进行反编译,重新得到与乘数αm相同格式的最终结果αp。另外,对数/反对数表中向量一列中含有数字0,该值无法用α的正整数次幂表示。此处借助补码的思想对该行进行处理,令向量0用十进制的127表示,实现了对数/反对数表的补全。对数/反对数表模块实际上采用组合逻辑电路定义了下述函数
| $ \operatorname{index}[\operatorname{alpha}[i]]=i. $ | (4) |
其中index函数执行向量转换为指数的操作,alpha函数表示由指数转换为向量的操作。在RTL设计过程中,由于BCH算法的参数固定,可以直接采用固定值查表的方法实现。如在BCH译码阶段求伴随式计算,方程(2)可以转换为
| $ \begin{gathered} S_i=\sum\limits_{j=0}^{n-1} r\left(\alpha^i\right)^j=\sum\limits_{j=0}^{n-1} r \times \text { alpha }\left\{\operatorname{index}\left[\left(\alpha^i\right)^j\right]\right\}= \\ \sum\limits_{j=0}^{n-1} r \times \text { alpha }\{[i \times j \% \mathrm{n}]\} . \end{gathered} $ | (5) |
由于r的数值为0或1,上式中的r后第1个“×”在实际电路中为逻辑判断,r=0时表示此项的乘积不参与求和,对应的电路流程图如图 3(b)所示。
|
Download:
|
| 图 3 BCH译码算法的框图 Fig. 3 Block diagram of BCH decoder | |
如图 3所示,在BM算法中需要进行多次迭代计算,当第j次迭代计算的差值结果dj不为0时,需要查找历史数据中,满足i-L(i)最大且d不为0两个条件的第i次,将di和dj代入错误位置多项式迭代方程获得新的错误位置多项式。然而,在RTL实现时,如果BCH码的纠错能力很强,使用寄存器保存历史数据d和L会消耗大量的寄存器。
借用冒泡排序的思想可以有效地解决这一矛盾。通过声明少数寄存器作为临时存储池,每当新的dj产生,若此时的j-L(j)更大,则保留此dj,作为下一次d不为0时迭代的di。特殊地,当BM迭代处于第1次时,由于i的初始值为0,则i-L(i)也为0。这种方式极大地减少了寄存器的消耗,在大容量纠错码的实现中极为有效。
2.3 顶层接口经过上述优化,本文实现了一种面向PUF的大纠错容量模糊提取器,由于芯片设计的需求未搭载AMBA总线,为保证IP后续拓展的易用性,本设计的接口协议采用私有接口协议,使用简单的valid-ready协议完成127 bit长度的模糊提取器。其接口命名如表 2所示。
|
|
表 2 模糊提取器顶层接口与功能描述 Table 2 Fuzzy extractor interface and function description |
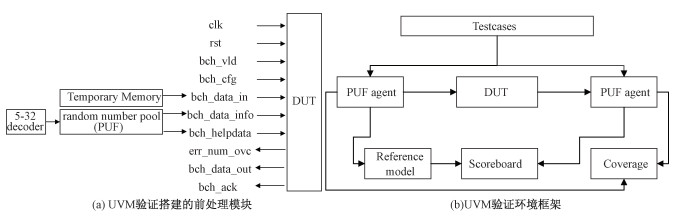
本部分借助UVM验证框架,面向上述待测模块(design under test,DUT),构建必要的前处理模块并搭建完善的验证环境。如图 4(a)所示,由于模糊提取器模块主要包括注册和工作2种功能,借助systemverilog设置了虚线框内的前处理模块,主要包括5 bit地址译码器、临时存储(保存帮助文件H)和PUF等。在前处理模块的基础上,搭建的验证环境框架如图 4(b)所示。
|
Download:
|
| 图 4 UVM验证环境框图 Fig. 4 Block diagram of UVM verification environment | |
验证框架同样基于systemverilog搭建,主要由代理模块(agent)、覆盖率模块(coverage)、参考模型(reference model)、计分板(scoreboard)及DUT构成。该验证环境中agent主要用于模拟上游master的行为推进验证流程,agent中的驱动(driver)只关注底层逻辑实现,监视器(monitor)监控采样底层数据组(transaction),传递给其他模块。coverage主要针对DUT中描述的各个工作模式进行覆盖率检测,侧重不同挑战信号和响应信号的覆盖支持。用回调函数(callback)和命令序列列表(command sequence list)进行采样,整个环境的覆盖率收集结果写入同一个日志文件中。参考模型用C语言实现,模拟模糊提取器中各个状态的行为,将输出传递给scoreboard和DUT响应信号进行比较。本环境使用应用程序接口(application programming interface,API)实现C语言函数在UVM中的调用。Scoreboard主要负责接收agent获得的DUT响应信号以及参考模型提供的期望响应,并进行比较,得到验证结果。
3.2 验证功能点分解对DUT的功能点分解,需要进行验证的分项包含:时钟复位(Clock & Reset)、工作模式验证和异常检验。具体分解如表 3所示。
|
|
表 3 DUT验证功能点分解列表 Table 3 Function list of DUT verification |
Clock & Reset主要验证DUT常规功能点,检验该DUT时钟和复位是否正常。模式验证的目的是验证实际场景验证相关状态是否可以正常工作(具体分为注册、工作和debug3种状态),仿真可能产生的各种真实使用场景,进行随机状态验证。异常检验主要模拟实际工作时可能发生的异常状态,进行检验。
3.3 测试用例设计针对功能点设计测试用例,具体测试用例覆盖功能点情况如表 4所示。通过9个测试样例对10个功能点进行了全覆盖。通过查看代码覆盖率和功能覆盖率,改进分析过程,完善RTL代码,保证语句、状态机、路径、信号切换、分支覆盖率达到标准,功能点全覆盖。
|
|
表 4 UVM样例及覆盖功能点列表 Table 4 List of UVM case and function |
此次验证使用VCS工具对模糊提取器模块进行UVM验证,验证通过后进行覆盖率收集,其结果在本部分进行展示。
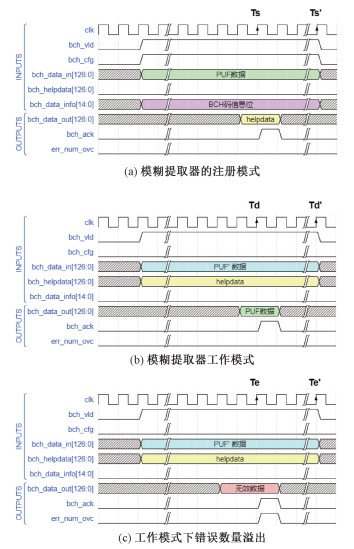
对于UVM回归验证,需要对模糊提取器的单个样例波形示意图进行描述。图 5(a)对应表 3功能点4,在bch_vld和bch_cfg接口同时为高电平时,模糊提取器进入注册模式;与此同时PUF数据和BCH码信息位视为有效,进入算法内部进行计算;在Ts时刻产生持续时长为1时钟周期的bch_ack脉冲信号,此周期中bch_data_out端输出的helpdata数据有效;外部逻辑在任意Ts’时刻拉低,结束样例。图 5(b)对应功能点5,bch_cfg保持低电平时,bch_vld拉高使得模糊提取器进入工作模式,此时输入端的PUF’数据(可能产生变化的PUF数据)和helpdata为有效;在Td时刻产生持续时长为1时钟周期的bch_ack脉冲信号,此时bch_data_out端输出的PUF数据有效,该数据的输出实现了对PUF’数据的还原;外部逻辑在任意Td’时刻拉低,结束样例图 5(c)对应功能点10。相比较于图 5(b),若模糊提取器计算过程中出现错误或者识别到错误的位数超出了BCH码的纠错能力,则err_num_ovc端口在Te时刻与bch_ack同时输出1时钟周期的脉冲,且此时外部逻辑认为bch_data_out数据无效。基于上述样例覆盖的UVM回归验证的结果表明,模糊提取器的设计能够满足预期的功能需求。
|
Download:
|
| 图 5 模糊提取器在多种模式下的接口时序图 Fig. 5 Interface sequence diagram of fuzzy extractor in multiple modes | |
代码覆盖率主要包括语句覆盖率、信号切换覆盖率、状态机覆盖率、条件覆盖率和分支覆盖率5种类型。语句覆盖率用于度量代码行是否执行,所添加的可忽略部分(exclusion)为正常情况下case块中不会执行的default语句;信号切换覆盖率主要度量单位变量的01切换是否执行,所添加的exclusion为忽略常数的01切换、忽略设计基于其他考虑使用的多余单位变量等部分。状态机覆盖率度量状态机中访问过的状态和切换,添加的exclusion为忽略正常状态下不会执行的其他状态与IDLE/DEFAULT状态之间的跳转;条件覆盖率度量条件表达式中所有条件是否都有成立与否发生,通常要求完成全覆盖;分支覆盖率度量所有判定的分支是否执行,添加的exclusion主要为忽略default代码块所包含的分支。图 6(a)为直接统计的不添加exclusion的代码覆盖率,基于设计的可预期情况添加exclusion后的代码覆盖率如图 6(b)所示。添加必要的exclusion后,代码覆盖率达到100%。

|
Download:
|
| 图 6 模糊提取器的UVM覆盖率报告 Fig. 6 UVM coverage reports for fuzzy extractor | |
除模糊提取器外,测试芯片还搭载了UART接口逻辑、控制模块和研究团队设计的SRAM PUF,所有数字逻辑处于单一时钟域,设计时钟频率为SS_1.35V_125C@16.7 MHz,综合结果显示,模糊提取器部分占用芯片面积306 267 μm2,以标准单元NAND2HD1X计算得消耗逻辑门数量约为50 609。
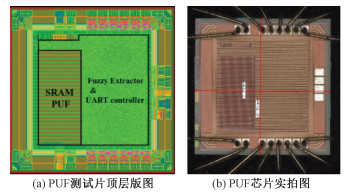
该设计在华虹宏力110 nm CMOS平台流片,最终全芯片含IO尺寸为1 140 μm×1 140 μm,芯片顶层版图如图 7(a)侧所示。该芯片搭载了课题组自研的SRAM PUF模块、模糊提取器和UART接口逻辑,芯片外围为电源、地、GPIO和IO filler。图 7(b)右侧展示了芯片裸片在SOP16塑料管壳中打线的实物图,裸片厚度480 μm。
|
Download:
|
| 图 7 PUF测试片版图和实拍图 Fig. 7 PUF test chip layout and photo | |
根据芯片的管脚定义,我们设计了如图 8(a)所示的测试板,测试板上搭载SOP16烧录座,方便进行芯片的更换。文献[27]展示了对于该芯片的SRAM PUF模块的测试。同时,我们也进行了模糊提取器的功能测试。测试环境使用STM32F407ZGT6开发板做上位机控制PUF芯片的工作状态,并将读取到的数据通过串口转USB上传到PC进行整理。图 8(b)和8(c)展示了测试系统和连接关系示意图。

|
Download:
|
| 图 8 PUF芯片的测试系统 Fig. 8 PUF chip test system | |
测试结果表明,模糊提取器在PUF数据发生波动的情况下具有数据还原能力,可以满足PUF芯片稳定的挑战-相应关系。功耗方面,在典型工作状态中实测全芯片功耗为1.79 mW,静态电流为11 nA。
4.3 性能比较PUF模块在实际测试之前无法预估和仿真不稳定位的数量,因此相比较于其他场景的纠错码实现,面向PUF的模糊提取器纠错容量通常会设置一定的冗余以保证稳定的数据还原能力。表 5中NAND Flash数据纠错和短极化码算法优化的场景中,使用的BCH码纠错容量均小于本设计方案。除此以外,在不使用冒泡存储方案的情况下,大纠错容量的参数选择会显著提升逻辑单元数量,因此常规的PUF模糊提取器会对该参数做出取舍,通过降低一定的纠错容量换取更小的芯片面积或FPGA资源消耗。
|
|
表 5 相似功能实现的参数对比表 Table 5 Comparison of parameters of similar implementations |
本文设计了一种面向PUF的大纠错容量的模糊提取器,该模糊提取器兼容的码长为127 bit,纠错容量为27 bit。通过向模糊提取器中的BCH码算法引入对数/反对数表避免了大量使用有限域乘法器和求逆运算;借助冒泡存储的方式减少了BM算法中历史数据的寄存器占用。UVM验证的结果显示,本设计在满足功能点的同时,具有良好的代码风格,可以达到100%的覆盖率。经过流片及测试,结果表明,该模糊提取器设计可以满足SRAM PUF不稳定位的纠错需求,稳定实现其挑战相应功能。
| [1] |
Satpathy S, Mathew S, Li J T, et al. 13fJ/bit probing-resilient 250K PUF array with soft darkbit masking for 1.94% bit-error in 22 nm tri-gate CMOS[C]//ESSCIRC 2014-40th European Solid State Circuits Conference (ESSCIRC). September 22-26, 2014, Venice Lido, Italy. IEEE, 2014: 239-242. DOI: 10.1109/ESSCIRC.2014.6942066.
|
| [2] |
Su Y, Holleman J, Otis B. A 1.6pJ/bit 96% stable chip-ID generating circuit using process variations[C]//2007 IEEE International Solid-State Circuits Conference. Digest of Technical Papers. February 11-15, 2007, San Francisco, CA, USA. IEEE, 2007: 406-611. DOI: 10.1109/ISSCC.2007.373466.
|
| [3] |
Lin L, Srivathsa S, Krishnappa D K, et al. Design and validation of arbiter-based PUFs for sub-45-nm low-power security applications[J]. IEEE Transactions on Information Forensics and Security, 2012, 7(4): 1394-1403. Doi:10.1109/TIFS.2012.2195174 |
| [4] |
Lin L, Holcomb D, Krishnappa D K, et al. Low-power sub-threshold design of secure physical unclonable functions[C]//2010 ACM/IEEE International Symposium on Low-Power Electronics and Design. August 18-20, 2010, Austin, TX, USA. IEEE, 2010: 43-48. DOI: 10.1145/1840845.1840855.
|
| [5] |
Maes R, Verbauwhede I. Physically unclonable functions: a study on the state of the art and future research directions[M]//Towards hardware-intrinsic security. Springer, Berlin, Heidelberg, 2010: 3-37. DOI: 10.1007/978-3-642-14452-3_1.
|
| [6] |
Suh G E, Devadas S. Physical unclonable functions for device authentication and secret key generation[C]//2007 44th ACM/IEEE Design Automation Conference. June 4-8, 2007. San Diego, CA, USA. IEEE, 2007: 9-14. DOI: 10.1109/dac.2007.375043.
|
| [7] |
Guajardo J, Kumar S S, Schrijen G J, et al. FPGA intrinsic PUFs and their use for IP protection[C]//Cryptographic Hardware and Embedded Systems-CHES 2007, 2007: 63-80. DOI: 10.1007/978-3-540-74735-2_5.
|
| [8] |
Alheyasat A, Torrens G, Bota S, et al. Bit-cell selection analysis for embedded SRAM-based PUF[C]//2020 IEEE International Symposium on Circuits and Systems. October 12-14, 2020, Seville, Spain. IEEE, 2020: 1-4. DOI: 10.1109/ISCAS45731.2020.9180780.
|
| [9] |
Kim J S, Patel M, Hassan H, et al. The DRAM latency PUF: quickly evaluating physical unclonable functions by exploiting the latency-reliability tradeoff in modern commodity DRAM devices[C]//2018 IEEE International Symposium on High Performance Computer Architecture. February 24-28, 2018, Vienna, Austria. IEEE, 2018: 194-207. DOI: 10.1109/HPCA.2018.00026.
|
| [10] |
Ni L, Wang P J, Zhang Y J, et al. A reliable multi-information entropy glitch PUF using schmitt trigger sampling method for IoT security[C]//2021 IEEE 14th International Conference on ASIC. October 26-29, 2021, Kunming, China. IEEE, 2021: 1-4. DOI: 10.1109/ASICON52560.2021.9620406.
|
| [11] |
Shifman Y, Miller A, Weizman Y, et al. An SRAM PUF with 2 independent bits/cell in 65 nm[C]//2019 IEEE International Symposium on Circuits and Systems. May 26-29, 2019, Sapporo, Japan. IEEE, 2019: 1-5. DOI: 10.1109/ISCAS.2019.8702612.
|
| [12] |
Pang Y C, Wu H Q, Gao B, et al. A novel PUF against machine learning attack: implementation on a 16 Mb RRAM chip[C]//2017 IEEE International Electron Devices Meeting. December 2-6, 2017, San Francisco, CA, USA. IEEE, 2017: 12.2.1-12.2.4. DOI: 10.1109/IEDM.2017.8268376.
|
| [13] |
Satpathy S, Mathew S K, Suresh V, et al. A 4-fJ/b delay-hardened physically unclonable function circuit with selective bit destabilization in 14-nm trigate CMOS[J]. IEEE Journal of Solid-State Circuits, 2017, 52(4): 940-949. Doi:10.1109/JSSC.2016.2636859 |
| [14] |
Dodis Y, Reyzin L, Smith A. Fuzzy extractors: how to generate strong keys from biometrics and other noisy data[M]//Advances in Cryptology-EUROCRYPT 2004. Berlin, Heidelberg: Springer Berlin Heidelberg, 2004: 523-540. DOI: 10.1007/978-3-540-24676-3_31.
|
| [15] |
Tuyls P, Akkermans A H M, Kevenaar T A M, et al. Practical biometric authentication with template protection[C]//Audio- and Video-Based Biometric Person Authentication, 2005: 436-446. DOI: 10.1007/11527923_45.
|
| [16] |
Hao F, Anderson R, Daugman J. Combining crypto with biometrics effectively[J]. IEEE Transactions on Computers, 2006, 55(9): 1081-1088. Doi:10.1109/TC.2006.138 |
| [17] |
van der Veen M, Kevenaar T, Schrijen G J, et al. Face biometrics with renewable templates[C]//Proc SPIE 6072, Security, Steganography, and Watermarking of Multimedia Contents Ⅷ, 2006, 6072: 205-216. DOI: 10.1117/12.643176.
|
| [18] |
Bösch C, Guajardo J, Sadeghi A R, et al. Efficient helper data key extractor on FPGAs[C]//Cryptographic Hardware and Embedded Systems-CHES 2008, 2008: 181-197. DOI: 10.1007/978-3-540-85053-3_12.
|
| [19] |
Becker G T. Robust fuzzy extractors and helper data manipulation attacks revisited: theory versus practice[J]. IEEE Transactions on Dependable and Secure Computing, 2019, 16(5): 783-795. Doi:10.1109/tdsc.2017.2762675 |
| [20] |
Dodis Y, Katz J, Reyzin L, et al. Robust fuzzy extractors and authenticated key agreement from close secrets[C]//Advances in Cryptology-CRYPTO 2006, 2006: 232-250. DOI: 10.1007/11818175_14.
|
| [21] |
Potey S D, Dhande P M. Error detection and correction capability for BCH encoder using VHDL[C]//2019 IEEE 5th International Conference for Convergence in Technology (I2CT). March 29-31, 2019, Bombay, India. IEEE, 2019: 1-4. DOI: 10.1109/I2CT45611.2019.9033847.
|
| [22] |
Bromley J. If SystemVerilog is so good, why do we need the UVM? Sharing responsibilities between libraries and the core language[C]//Proceedings of the 2013 Forum on specification and Design Languages (FDL). September 24-26, 2013, Paris, France. IEEE, 2013: 1-7.
|
| [23] |
刘登科, 刘伟, 宋贺伦, 等. 一种0.11μm SRAM PUF芯片的测试与分析[J]. 电子测量技术, 2019, 42(17): 88-94. Doi:10.19651/j.cnki.emt.1902719 |
| [24] |
Xiao K, Rahman M T, Forte D, et al. Bit selection algorithm suitable for high-volume production of SRAM-PUF[C]//2014 IEEE International Symposium on Hardware-Oriented Security and Trust. May 6-7, 2014, Arlington, VA, USA. IEEE, 2014: 101-106. DOI: 10.1109/HST.2014.6855578.
|
| [25] |
Liu M Q, Zhou C, Tang Q Y, et al. A data remanence based approach to generate 100% stable keys from an SRAM physical unclonable function[C]//2017 IEEE/ACM International Symposium on Low Power Electronics and Design (ISLPED). July 24-26, 2017, Taipei, Taiwan, China. IEEE, 2017: 1-6. DOI: 10.1109/ISLPED.2017.8009192.
|
| [26] |
江建国. BCH编译码器的设计及验证[D]. 上海: 上海交通大学, 2011.
|
| [27] |
张家梁, 宋贺伦. 一种基于BCH算法的SRAM PUF芯片的设计、测试与分析[J]. 电子测量技术, 2021, 44(6): 28-35. Doi:10.19651/j.cnki.emt.2105822 |
| [28] |
奚珍珍, 刘顺兰. 一种基于BCH级联极化码的分段校验译码算法[J]. 软件导刊, 2021, 20(9): 191-195. Doi:10.11907/rjdk.202436 |
| [29] |
Shifman Y, Miller A, Keren O, et al. An SRAM-based PUF with a capacitive digital preselection for a 1E-9 key error probability[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2020, 67(12): 4855-4868. Doi:10.1109/TCSI.2020.2996772 |
| [30] |
Korenda A R, Assiri S, Afghah F, et al. An error correction approach to memristors PUF-based key encapsulation[C]//2021 IEEE International Conference on Omni-Layer Intelligent Systems. August 23-25, 2021, Barcelona, Spain. IEEE, 2021: 1-6. DOI: 10.1109/COINS51742.2021.9524282.
|
 2024, Vol. 41
2024, Vol. 41 


