同轴旋转圆柱之间的流动被称为Taylor-Couette(TC)流动，该模型在工业生产中有着广泛的应用，如化工分离装置、石油开采中的钻井设备、核电主泵等旋转设备^[1-3]。同时TC系统也是地球物理和天体物理中研究大气环流^[4]、黑洞吸积盘^[5]等问题的常用模型。

TC流动是流体动力学和非线性系统研究的经典问题，最早由牛顿提出，在1923年Taylor首先对该模型进行了理论分析。早期对TC流动的研究主要集中在等温系统中，直到20世纪60年代，研究人员开始关注施加径向温度梯度的TC流动。1964年，Snyder和Karlsson^[6]在施加径向温度梯度的TC系统中开展实验研究，发现较大温差促使流动失稳，小温差使流动更加稳定。1990年Ali和Weidman^[7]进行了稳定性分析，在轴向无限长的TC系统中讨论普朗特数和半径比对流动稳定性的影响。2013年Yoshikawa等^[8]在此基础上引入能量分析，讨论了离心浮力的影响。Ball等^[9-12]通过大量的实验和数值研究讨论小高宽比模型中的TC流动，报道了在浮力和离心力共同作用下螺旋涡流动的演化过程，并发现可以利用混合对流参数来划分不同的三维流动区域。2008年Lepiller等^[13]通过实验进一步讨论了TC系统中螺旋涡流的形成过程及其变化规律，发现径向温度梯度促进流动失稳，导致螺旋状涡流动，且螺旋结构首先出现在腔体底部。2015年，Kang等^[14]基于上述实验进行了数值研究，得到了与实验一致的结果并进一步揭示了从同向旋转涡流动发展为反向旋转涡流动的二次失稳机理及相应的传热规律。2015年Lopez等^[15]进行了稳定性分析和数值研究，重点讨论空气在轴向有限长TC系统和轴向无限长TC系统中流动特征和传热性能上的差异。2017年，Kang等^[16]通过数值模拟讨论不同普朗特数流体的TC流动，发现正径向温度梯度使流动稳定，负径向温度梯度促使流动失稳。2022年，Leng和Zhong^[17]讨论空气和水的TC湍流，给出了不同温差条件下内圆柱转速增大时流态的演化，并指出系统传热速率和角动量随转速的变化趋势相似。

以上研究均以Oberbeck-Boussinesq(OB)近似下的流体作为工质，即认为流体的密度和温度满足线性关系，然而在实际工程应用中采用的流动工质往往不满足这一假设，比如具有密度倒置特性的冷水和镓、铋等金属熔体。其中，冷水的对流传热在实际工程应用中十分常见，如蓄冷系统中的融冰过程等。相关研究主要集中在矩形腔、圆柱腔内的自然对流^[18-26]，揭示了密度倒置参数对传热性能的重要影响。对于存在径向温度梯度的侧加热竖直环形腔中冷水热对流问题的研究较少。1987年Lin和Nansteel^[27]，1990年Ho和Lin^[28]分别讨论了恒温和恒热流边界条件下侧加热竖直环形腔中冷水的自然对流，报道了因冷水的密度倒置现象导致传热出现固有低值。1998年Ho和Tu ^[29]重点研究了该模型中冷水自然对流的流态演化。在内圆柱旋转的TC系统中，关于径向温度梯度下冷水热对流问题的研究更少，1992年Ho和Tu ^[30]重点讨论内圆柱旋转对传热的增强效果，1993年Ho和Tu^[31]又在高宽比为8的竖直环形腔中进一步研究了内圆柱旋转时冷水从稳态对流到振荡对流的演化。然而，上述竖直环形腔内冷水热对流的数值研究均采用了轴对称假设。本文认为，在离心力和浮力的共同作用下，竖直环形腔内流动比较复杂，冷水的密度倒置特性导致流动进一步复杂化，在数值模型中采用轴对称假设无法捕捉流动的周向变化特征，导致对传热特性的预测不够准确。因此，有必要开展三维数值模拟研究。

根据我们掌握的文献资料，目前尚没有针对冷水在TC流动中的三维流动结构的研究。为此本文首次使用三维数值模拟方法，采用与Ho和Tu^[31]相同的几何模型，讨论不同参数条件下冷水在TC系统中的流动特征和传热特性。

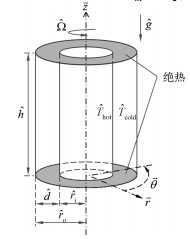
1 模型和数值方法

本文考察两同轴圆柱间的TC流动，物理模型如图 1所示，内圆柱半径为$\hat{r}_{\mathrm{i}}$($\widehat \cdot$表示有量纲的物理量)，外圆柱半径为$\hat{r}_{\mathrm{o}}$，两圆柱间隙为$\widehat d$，圆柱轴向高度为$\widehat h$，模型内外圆柱半径比η=$\hat{r}_{\mathrm{i}} / \hat{r}_{\mathrm{o}}=0.5$，竖直环形腔的高宽比为$\mathit{\Gamma}=\hat{h} / \hat{d}=8$。此外，旋转模型中内圆柱以角速度$\widehat \Omega$匀速旋转，外圆柱保持静止，内、外圆柱的温度恒定，分别为$\hat{T}_{\text {hot }}$和$\hat{T}_{\text {cold }}\left(\hat{T}_{\text {hot }}>\hat{T}_{\text {cold }}\right)$，上下端面绝热静止。

为简化模型，假设流体为不可压缩牛顿流体，忽略黏性耗散，忽略离心力导致的浮力^{[12, 30-32]}，仅在重力项中考虑密度对温度的依赖性，其余物性参数均设为常数。密度与温度之间的函数关系采用Gebhart和Mollendorf ^[33]提出的非线性密度公式

$\hat{\rho}(\hat{T})=\hat{\rho}_m\left[1-\hat{\gamma}\left|\hat{T}-\hat{T}_m\right|^q\right] .$

(1)

其中：$\hat{\rho}_m$=999.972 kg/m³为密度极大值，$\hat{\gamma}$=9.297 173×10^-6(℃)^-q为热膨胀系数，$\hat{T}_m$=4.029 325 ℃为密度极值对应的温度，指数q=1.894 816。

以$\hat{d}, \hat{d}^2 \hat{\nu}_m^{-1}, \hat{\nu}_m \hat{d}^{-1}, \Delta \hat{T}\left(\Delta \hat{T}=\hat{T}_{\mathrm{hot}}-\hat{T}_{\text {cold }}\right)$和$\hat{\boldsymbol{\rho}}_m \hat{\nu}_m^2 \hat{d}^{-2}$分别作为长度、时间、速度、温度和压力的特征尺度，得到无量纲控制方程：

$\nabla \cdot \boldsymbol{u}=0,$

(2)

$\begin{gathered} \frac{\partial \boldsymbol{u}}{\partial t}+\boldsymbol{u} \cdot \nabla \boldsymbol{u}=-\nabla p+\nabla^2 \boldsymbol{u}+ \\ {RaPr}^{-1}\left|\mathit{\Theta } - {\mathit{\Theta }_m}\right|{ }^q \boldsymbol{n}_z, \end{gathered}$

(3)

$\frac{\partial \mathit{\Theta }}{\partial t}+\boldsymbol{u} \cdot \nabla \mathit{\Theta }={Pr}^{-1} \nabla^2 \mathit{\Theta }.$

(4)

其中：u 为速度，t为时间，p为压力，Θ为温度，Θ的定义为$\left(\hat{T}-\hat{T}_{\text {cold }}\right) / \Delta \hat{T}, \boldsymbol{n}_z$为轴向单位向量。方程中的无量纲控制参数包括：瑞利数Ra、普朗特数Pr和密度倒置参数Θ_m, 定义如下：

$Ra=\hat{g} \hat{\gamma}(\Delta \hat{T})^q \hat{d}^3 \hat{\nu}_m^{-1} \hat{\alpha}_m{ }^{-1} .$

(5)

${Pr}=\hat{\nu}_m \hat{\alpha}_m^{-1} .$

(6)

$\mathit{\Theta}_m=\left(\hat{T}_m-\hat{T}_{\text {cold }}\right) /\left(\hat{T}_{\text {hot }}-\hat{T}_{\text {cold }}\right) .$

(7)

其中$\hat{g}$(ms^-2) 为重力加速度，$\hat{\nu}_m$ (m²s^-1)和$\hat{\alpha}_m$ (m²s^-1)分别为密度极值温度$\hat{T}_m$时水的运动黏性系数和热扩散系数，冷水普朗特数为11.57。同时，为了定量刻画内圆柱旋转速度引入雷诺数

$Re = {\hat r_{\rm{i}}}\mathit{\hat \Omega }\hat d\hat \nu _m^{ - 1}.$

(8)

并使用混合对流参数σ来定量描述浮力与离心力的关系^{[12, 32]}

$\sigma={RaPr}^{-1} {Re}^{-2}.$

(9)

显然σ越小，离心力作用越显著。

本文采用的边界条件如下：

$\begin{array}{lll} u_r=u_z=0, u_\theta=R e & \text { at } & r=\eta(1-\eta), \\ \boldsymbol{u}=0 & \text { at } & r=1 /(1-\eta), z=0, z=\mathit{\Gamma}, \\ \mathit{\Theta }=0 & \text { at } & r=\eta(1-\eta), \\ \mathit{\Theta }=1 & \text { at } & r=1 /(1-\eta), \\ \partial \mathit{\Theta } / \partial z=0 & \text { at } & z=0, z=\mathit{\Gamma} . \end{array}$

(10)

为降低计算成本，首先模拟了低Ra和Re时的流动和传热过程，此时初始条件设置为腔体内流体静止，速度u=0，温度Θ=0.5；内圆柱有恒定转速，周向速度u_θ=Re，温度为Θ=1；外圆柱和上下端面均保持静止，初始温度为Θ=0。随后以低Ra和Re的模拟结果作为初始条件，通过逐步提高Ra和Re得到不同参数条件下的模拟结果。

使用有限体积方法进行数值计算，通过PISO(pressure-implicit with splitting of operators)算法对速度压力进行解耦。此外，动量和温度方程中的时间项采用二阶Crank-Nicholson格式进行离散，对流项使用二阶迎风格式进行离散，扩散项则采用二阶中心差分格式进行离散。无量纲时间步长在5×10^-5~2×10^-3。在每一个时间步内，动量和温度方程的残差小于10^-7时认为该时间步内迭代计算收敛。

为保证计算方法的可靠性和计算结果的准确性，本文进行了多组算法检验。系统传热性能是冷水对流传热问题考察和分析的重点，等效导热系数是对流传热与热传导时换热系数的比值^[10]，对于非等温TC流动，等效导热系数是量化系统传热性能的重要指标^[34-35]，是算法检验过程中需要考察的重要参数。参考已有的研究，本文中内、外圆柱面上的局部等效导热系数定义为：

$\kappa_{\text {eqi }}=-\left.\frac{\eta}{(\eta-1)} \ln \eta \cdot \partial_r \mathit{\Theta }\right|_{r=\eta /(1-\eta)},$

(11)

$\kappa_{\text {eqo }}=-\left.\frac{1}{(\eta-1)} \ln \eta \cdot \partial_r \mathit{\Theta }\right|_{r=1 /(1-\eta)} .$

(12)

等效导热系数定义为：

$\overline{\kappa_{\text {eqi }}}=\frac{1}{2 \pi \mathit{\Gamma }} \int_0^{2 \pi} \int_0^{\mathit{\Gamma }} \kappa_{\text {eqi }} \mathrm{d} z \mathrm{d} \theta,$

(13)

$\overline{\kappa_{\text {eqo }}}=\frac{1}{2 \pi \mathit{\Gamma }} \int_0^{2 \pi} \int_0^{\mathit{\Gamma }} \kappa_{\text {eqo }} \mathrm{d} z \mathrm{d} \theta .$

(14)

时间平均的等效导热系数定义为：

$\left\langle\overline{\kappa_{\text {eqi }}}\right\rangle_t=\frac{1}{2 \pi \mathit{\Gamma } t_p} \int_{t_0}^{t_0+t_p} \int_0^{2 \pi} \int_0^{\mathit{\Gamma }} \kappa_{\text {eqi }} \mathrm{d} z \mathrm{~d} \theta \mathrm{d} t,$

(15)

$\left\langle\overline{\kappa_{\text {eqo }}}\right\rangle_t=\frac{1}{2 \pi \mathit{\Gamma } t_p} \int_{t_0}^{t_0+t_p} \int_0^{2 \pi} \int_0^{\mathit{\Gamma }} \kappa_{\text {eqo }} \mathrm{d} z \mathrm{~d} \theta \mathrm{d} t .$

(16)

表 1列出了高宽比A_y=8，长宽比A_z=2的侧加热矩形腔中，Θ_m=0.5的冷水在Ra=10⁵时自然对流的振荡传热结果，表中数据显示本文计算的振荡传热结果与文献[26]结果吻合。此外，选取与文献[29, 31]中竖直环形腔高宽比、半径比相同的模型进行三维数值模拟，采用相同Pr数，考察存在径向温度梯度的竖直环形腔中Θ_m=0.5的冷水在Ra=6×10⁴时的自然对流，以及Ra=10⁴，Re=50时内圆柱旋转的混合对流。如表 2所示，本文的振荡传热结果与文献[29, 31]结果有很好的一致性。同时，本文得到的流场和温度场特征均与文献一致。通过上述检验，可以证实本文数值方法的可靠性。

2 结果分析与讨论 2.1 网格独立性检验

数值求解过程中采用非均匀网格，径向和轴向网格在壁面附近加密，周向使用均匀网格。选取Θ_m=0.5，Re=150时的2个典型工况开展网格独立性分析。此时系统的传热速率和流动振荡频率如表 3所示，其中Ra=10⁶，Re=150时流态为混沌振荡对流，没有明显的主频率。结果表明，M2网格与M3网格之间$\left\langle\overline{\kappa_{\mathrm{eqi}}}\right\rangle_t$的误差小于0.3 %，频率f的误差小于1.5 %。综合考虑计算精度和效率，最终选用M2网格进行计算。

本文在10⁴≤Ra≤10⁶范围内对竖直环形腔中冷水自然对流(Re=0)和内圆柱旋转时(Re=30，50，100和150)的冷水TC流动进行了三维数值模拟。Θ_m=0.5时冷水的密度倒置特性尤为突出，因此，本文将以Θ_m=0.5的工况为主体展开讨论Ra，Re和密度倒置参数Θ_m的影响。

2.2 旋转系统中冷水的流动和传热特征

旋转系统中冷水的流态变化丰富，随着控制参数的变化可能出现稳态流动、周期振荡流动、准周期振荡流动和混沌振荡流动。为确定流动的状态，本文选取6个典型位置作为监测点：(1.5, 0, 2)，(1.5, 0, 4)，(1.5, π/2, 4)，(1.5, π, 4)，(1.5, 3π/2, 4)和(1.5, 0, 6)，当相邻时间步监测点处速度和温度的相对误差小于10^-5时，认为流动达到了稳态。而振荡流动的状态则通过监测点处速度时间序列的功率谱密度(power spectral density，PSD)结果判断。系统整体传热特征采用类似的方法进行分析。当相邻时间步等效导热系数$\overline{\boldsymbol{\kappa}_{\mathrm{eq}}}$的相对误差小于10^-5，且$\overline{\kappa_{\mathrm{eqi}}}$ 与$\overline{\kappa_{\mathrm{eqo}}}$之间相对误差小于0.1 % 时判定为稳态传热。对于振荡传热，选取内圆柱面上等效导热系数$\overline{\kappa_{\mathrm{eqi}}}$的时间序列进行PSD分析，进而确定系统的整体传热特征。此外，为了判断流动是否具有轴对称特征，本文选取z=0.5，z=2，z=4，z=6和z=7.5的典型平面内r=1.5处环线上温度和轴向速度以及5个典型平面上壁面处局部等效导热系数κ_eq进行监测，当各状态量波动值小于1 % 时认为流动是轴对称的。

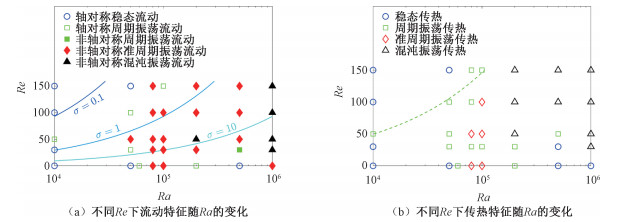
Ho和Tu^{[29, 31]}在TC系统中讨论冷水热对流时采用了轴对称假设，然而本文通过三维数值模拟研究冷水的TC流动时发现，随着Ra和Re的变化，在浮力和离心力的共同作用下，冷水呈现复杂的轴对称或非轴对称流动形态和传热特征。图 2(a)展示了参数空间中的流动特征，并通过σ来描述各工况浮力与离心力的相对大小。显然，自然对流的流动特征随Ra的变化十分复杂，流态首先由轴对称稳态流动发展为周期振荡流动，在Ra=8×10⁴和Ra=10⁵时出现非轴对称的准周期流动，随后恢复为轴对称的流动，直到Ra=10⁶时再次转变为准周期的非轴对称振荡流动。而在旋转系统中，随着Ra的增大，轴对称流态发展为非轴对称流态，流动的复杂度逐步提高。其中轴对称流态包括稳态流动和周期振荡对流，而非轴对称流态的流动特征更加复杂，包括周期、准周期和混沌振荡对流。图 2(b)中进一步给出了不同Re下传热特征随Ra的变化。自然对流条件下，Ho和Tu^[29]给出了Θ_m=0.5的冷水由稳态传热发展到周期振荡传热的临界瑞利数Ra_cr=5.200×10⁴±60。图 2(b)中相应工况的传热特征满足文献给出稳定性临界值。在冷水的TC流动中，低Ra时，得到的轴对称流态的传热特性与Ho和Tu^[31]采用轴对称假设得到的传热状态一致，图 2(b)中的绿色虚线为Ho和Tu^[31]给出的由稳态传热发展到振荡传热时稳定性临界曲线。而在高Ra条件下，计算结果与轴对称假设结果具有显著差异。Ho和Tu^[31]报道随着Ra增大，系统首先由稳态传热发展为振荡传热，随后又恢复到稳态传热。然而本文结果显示，随Ra增大流动混乱程度逐渐增强，系统的传热状态逐步发展为混沌振荡传热。上述差异表明：在高Ra情况下轴对称假设不再适用，有必要开展三维数值模拟研究。

2.3 流态演化

由图 2(a)可知，低Ra时流动基本为轴对称流态，此时流动结构相对简单，而高Ra时流动基本为非轴对称流态，且流动的复杂程度高。本节将分别讨论低Ra时和高Ra时的典型流态，对浮力和离心力共同作用下的流动特征和流态演化做进一步阐述。

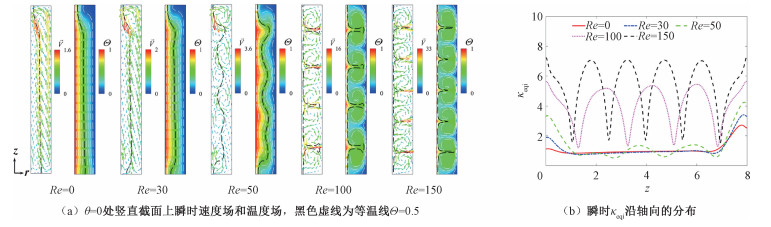
2.3.1 低Ra时的流态演化

图 3(a)以Θ_m=0.5，Ra=10⁴时的轴对称流动为例，展示了低Ra条件下随转速增加流动结构的变化。Re=0和Re=30时浮力主导流动，出现稳态的双层大尺度环流(bicellular large-scale circulation，bi-LSC)。LSC是浮力作用下流动的基础形态，然而与密度随温度单调变化的常规OB流体中仅有一个环流结构的LSC不同，冷水中出现的bi-LSC存在两个反向旋转的环流。这是由于冷水密度随温度非单调变化，靠近高温内圆柱和低温外圆柱的流体密度小，沿柱面向上流动，在Θ=0.5等温线附近密度大的流体则向下流动，从而在密度极值曲线两侧形成了两个反向旋转的大尺度环流。随Re的增加离心力作用增强，Re=50时bi-LSC中出现衍生的二次涡，密度极值曲线被扭曲，流动发展成为周期振荡的双层同向旋转涡(bicellular co-rotating vortices，bi-CoRV)流动。当内圆柱转速进一步提高，离心力主导流动，Re=100和Re=150时流态转变为稳态的泰勒涡流动(Taylor vortex flow，TVF)，此时密度极值曲线贴近内圆柱，并沿轴向出现反向旋转的周向涡对。

图 3(b)中给出了Θ_m=0.5，Ra=10⁴时轴对称流态局部传热速率随Re的变化。结合图 3(a)中对应工况竖直截面上的速度矢量场和温度场进行分析，发现当流体流向侧壁时热边界层变薄，内圆柱面上局部等效热导系数κ_eqi显著增加。浮力主导流动时，bi-LSC在热量传输中起主导作用，此时κ_eqi最大值出现在靠近端面的位置。Re=50时腔体中部出现明显径向流动，因此腔体中部区域κ_eqi增大且表现出与图 3(a)中温度场对应的波状分布特征。当Re增加到100和150时，径向流动进一步加强，腔体中部κ_eqi出现多个局部峰值且与端面附近κ_eqi大小接近。上述结果说明随着转速的提高，离心力作用下产生的周向涡流动将逐步取代浮力主导的大尺度环流，在此过程中腔体内的径向动量和热量输运得到了极大地加强。

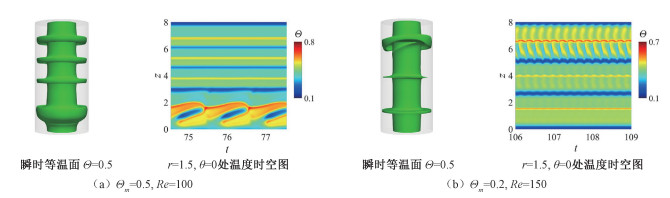
同时，低Ra条件下由振荡流动发展到稳态TVF的过程中出现了特殊的局部振荡流态，且密度倒置参数变化时，局部振荡流动出现的位置随之改变。图 4(a)以Ra=5×10⁴，Re=100时轴对称周期振荡流动为例展示了Θ_m=0.5时的典型局部振荡流态，此时腔体底部流场振荡。图 4(b)则以Ra=5×10⁴，Re=150时非轴对称周期振荡流动为例展示了Θ_m=0.2时的典型局部振荡流态，显然在腔体顶部区域出现振荡对流。随着密度倒置参数的变化，浮力作用下环形腔内主导流动的大尺度环流发生交替，在上下端面对旋转产生的Ekman涡的加强或抑制作用相反，因此不稳定振荡区域的位置与密度倒置参数的大小密切相关。此外，Θ_m=0.2时冷水中浮力和离心力的作用与采用常规OB流体时两种力的表现接近，此时仅在腔体上部区域出现流场振荡的流动与Kuo和Ball^[12]在Γ=10，η=0.5的模型中讨论空气TC流动时报道的局部振荡流动类似，这种流动的相似性进一步说明了本文计算结果的合理性。

2.3.2 高Ra时的流态演化

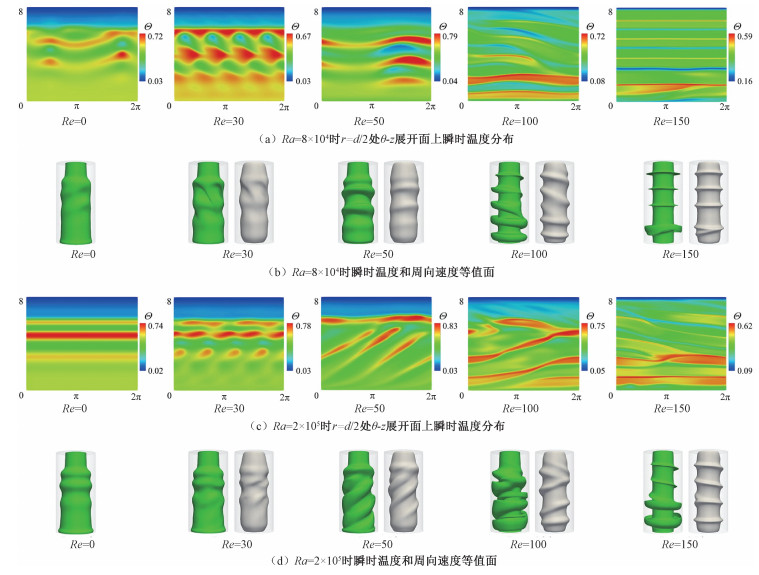
图 2(a)中结果显示Θ_m=0.5时，Ra≥8×10⁴的高Ra条件下，在Ra不同时流动特征随Re的变化有显著差异，本小节选取Ra=8×10⁴、Ra=2×10⁵时的流动，考察Re变化时非轴对称流态的演化。图 5(a)和5(b)展示了Ra=8×10⁴时不同Re下的温度场和速度场，在自然对流以及Re=30、50的混合对流中出现典型双层同向旋转波状涡(bicellular co-rotating wavy vortices，bi-CoRWV)流动。Re=100时，流态转变为向下倾斜的螺旋涡流动(spiral vortex flow with a negative inclination angle，SPI-n)。当Re=150时离心作用进一步增强，此时流动特征与图 4中Θ_m=0.5，Ra=5×10⁴，Re=100时类似，腔体上部出现稳定Taylor涡对，底部约1/3的区域出现不稳定振荡流动。图 5(c)和5(d)和展示了Ra=2×10⁵时不同Re下的流动结构，此时浮力作用显著增强，与相同转速条件Ra=8×10⁴时的流动存在明显形态差异。如图所示，随着Re的增加，流动首先由自然对流时周期振荡的轴对称bi-CoRV流动转变为Re=30时非轴对称的bi-CoRWV流动，随后发展为不同形态的螺旋涡流动(spiral vortex flow，SPI)，包括Re=50时向上倾斜的双层螺旋涡流动(bicellular spiral vortex flow with a positive inclination angle，bi-SPI-p)，Re=100时上倾螺旋和下倾螺旋同时存在的特殊螺旋涡流动(spiral vortex flow with two reversed inclination angles，SPI-r)和Re=150时的SPI-n。

显然，高Ra条件下流场中出现了丰富的非轴对称流动结构，相较于前人在常规流体中报道的波状涡流动和螺旋涡流动，冷水中的三维流态更为丰富。鉴于本文中浮力与离心力的作用机制与常规流体流动是一致的，下面结合常规流体中典型螺旋涡流动的产生条件进一步论述冷水中出现相应非轴对称流态的原因。在传统OB近似下，前人在研究TC系统中的螺旋涡流动时发现^[13-14]：内圆柱旋转方向一定时，SPI中螺旋结构倾斜方向由径向温度梯度符号决定。如在本文所采用内圆柱角速度方向与重力方向相反的模型中，常规流体在正的径向温度梯度下将出现SPI-n，在负的径向温度梯度下出现SPI-p。而本文中，负的径向温度梯度下，在Ra和Re变化过程中竖直环形腔内出现了SPI-n结构，因为螺旋结构倾斜方向实际由径向密度梯度决定。由于冷水的密度倒置特性，温度和密度不满足单调线性关系，因此尽管径向温度梯度恒小于0，但径向密度梯度取决于Θ_m。由图 5中Ra=8×10⁴，Re=100时温度等值面可知此时密度极值曲面靠近内圆柱，负的径向密度梯度主导流动，因此SPI的螺旋倾角为负。图 5中Ra=2×10⁵，Re=150时情况类似，流态表现为SPI-n。而Ra=2×10⁵，Re=50时浮力主导流动，正的径向密度梯度居主导地位，因此SPI螺旋倾角为正。此外，在Ra=2×10⁵，Re=100时流动更为特殊，此时腔体上部和底部的主导径向密度梯度符号相反，从而产生了上部为下倾螺旋，下部为上倾螺旋的特殊流态SPI-r。值得注意的是，这种结构在常规的OB流体中是不存在的，属于由密度极值现象导致的特殊螺旋涡流动结构。

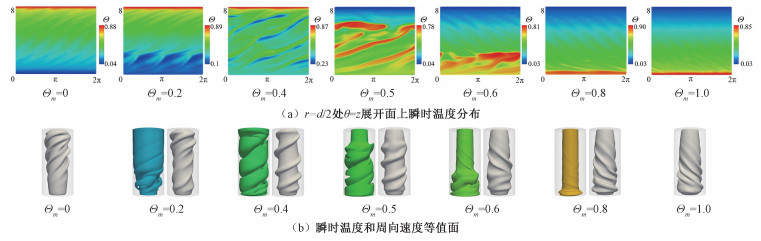
图 6进一步展示了Ra=5×10⁵，Re=100时不同密度倒置参数条件下的三维流动结构。显然，螺旋结构的倾斜方向与Θ_m密切相关，随着Θ_m的变化可以观察到3种不同类型螺旋涡流：SPI-p、SPI-r和SPI-n。其本质仍是径向密度梯度符号改变导致的螺旋倾角方向变化。Θ_m=0时，密度极大值出现在外侧低温圆柱面上，流场中居主导的径向密度梯度为正，流态表现为SPI-p，Θ_m=0.2和Θ_m=0.4时情况与Θ_m=0接近，密度极大值靠近外圆柱，因此出现SPI-p结构。Θ_m=0.5时流动表现为SPI-r，在正的径向密度梯度作用下，腔体下部出现SPI-p结构，而腔体顶部密度极值曲面贴近内圆柱，该区域出现SPI-n结构。Θ_m=0.6时流态同样为SPI-r，然而与Θ_m=0.5时不同，此时腔体上部SPI-n结构所在区域体积增大，SPI-p结构则仅存在于底部1/3区域内。随着Θ_m进一步增大，密度极值曲面逐步贴近内侧高温圆柱，在负的径向密度梯度作用下，Θ_m=0.8和Θ_m=1时出现了与Θ_m=0时相反的流型。

此外，对于常规流体的TC流动，端部圆环面的边界条件和腔体高宽比是影响流态的重要因素。本文中端面边界条件为绝热静止，是TC流动中较为常见的边界条件设置。此外，前人对端面采用恒温边界条件(一般为顶部端面低温，底部端面高温)的模型开展研究^[36-37]，此时流动存在轴向温度梯度，出现轴向分层流态。另有部分研究讨论了端面与内壁面同步旋转的TC流动模型^{[36, 38]}，这将改变端面处Ekman涡的旋转方向，进而影响整体流动结构。根据上述结果推测，在冷水的TC流动中，如果改变端面温度边界条件，设置轴向温差，在轴向温度梯度和径向温度梯度的共同作用下，流动中可能同时存在轴向分层和径向分层的结构，流动复杂度将进一步提高，相关流态变化规律有待后续研究；如果改变端面的速度边界条件，端面处Ekman涡的形态变化亦将进一步影响腔体中部的流动结构形态。对于传统流体，在高宽比较小的情况下，端面处产生的Ekman涡影响腔体中周向涡的尺寸和旋转方向^[38]，随着高宽比的增大，腔体中周向涡数量显著增加^[11]。在本文较小高宽比的模型中，如图 4所示，端面处Ekman涡与高Re下局部振荡流动的产生密切相关。根据上述结果推测，在冷水的TC流动中，随着高宽比的增大，竖直排列的周向涡数量增加，同时流动受端面处黏性阻力作用影响减小，腔体中部流动结构形态将更加规则，高Re下靠近端面附近的局部振荡区域体积减小。

图 7中展示了Θ_m=0.5时3个典型非轴对称流动工况的局部传热特征(为了更好地展示效果，图 7中外圆柱面展开图高宽比为实际比例的2倍)。如前所述，在流体流向侧壁时局部传热增强，因此图 7中κ_eq分布与图 5中相应流态结构具有一致性。如Ra=8×10⁴时的自然对流中κ_eq分布云图上出现波状条带结构，Re=100时则出现向下倾斜的螺旋状条带结构。在Ra=2×10⁵，Re=100时，内圆柱附近正的径向密度梯度主导流动，κ_eqi呈上倾螺旋分布，而外圆柱附近由负的径向密度梯度主导流动的区域，κ_eqo表现为下倾螺旋分布。此外，与图 3(b)中轴对称流态的局部传热特征相似，在浮力作用主导下，Ra=8×10⁴的自然对流中内圆柱面上局部传热最大值出现在靠近上端面的位置，外圆柱面上局部传热最大值出现在靠近下端面的位置。而Re=100的混合对流中，腔体中部离心力导致的周向涡极大地促进了径向动量和热量传输，使得内外圆柱中部的局部传热明显加强。此外，在Ra=8×10⁴，Re=100时，离心作用显著，受到Ekman效应影响，腔体底部流向外圆柱的径向流动被削弱，靠近下端面位置的κ_eqo明显减小。

2.4 系统整体传热

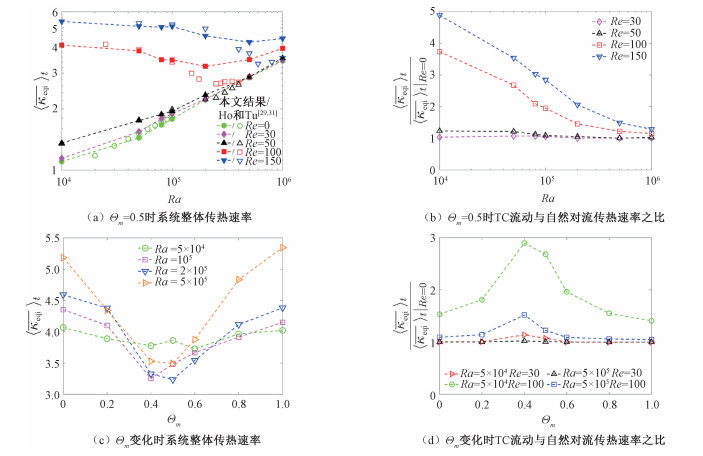
图 8(a)展示了Θ_m=0.5时，不同Re下时间平均的等效导热系数随Ra的变化。对于自然对流和内圆柱转速较低的混合对流，本文的三维数值模拟与Ho和Tu^{[29, 31]}采用轴对称假设得到的传热结果接近，此时随着Ra的增大浮力作用增强，端面处的径向流动强度显著提高，使系统传热速率单调增加。在高转速条件下，由于非轴对称流动结构的出现，本文与Ho和Tu^{[29, 31]}基于轴对称假设得到的对流传热速率存在显著差异。当Ra≥2×10⁵时，本文得到的传热速率明显高于基于轴对称假设的预测结果，在Ra=10⁶，Re=150时差异最大，此时本文得到的$\left\langle\overline{\kappa_{\mathrm{eqi}}}\right\rangle_t$比轴对称假设结果高24.7 %。此外，较高转速时由于三维流动结构改变，系统整体传热速率随Ra的增加呈现非单调变化趋势。下面以Re=100的工况为例，结合流态演化展开讨论。Ra=10⁴时流态为图 3(a)所示的TVF，此时腔体内竖直排列的Taylor涡是促进径向动量和热量传输的主要流动结构。Ra=8×10⁴时流态发展为图 5中展示的SPI-n，此时浮力作用增强，离心作用效果减弱，Taylor涡结构逐渐消失，径向热量传输被抑制。当Ra=2×10⁵时，浮力作用进一步增强，流态转变为SPI-r，端面处径向流动在系统热量传输中开始起主导作用。此后，端面处径向流动强度随Ra的增加不断提高，$\left\langle\overline{\kappa_{\mathrm{eqi}}}\right\rangle_t$亦随之增大。为定量刻画旋转对系统整体传热性能的强化效果，本文计算了不同Re下$\left\langle\overline{\kappa_{\mathrm{eqi}}}\right\rangle_t$与自然对流时$\left\langle\overline{\kappa_{\mathrm{eqi}}}\right\rangle_t$|_Re=0的比值随Ra的变化。如图 8(b)所示，Re=100和Re=150时旋转的传热强化效果远高于低转速情况。在本文参数范围内，Θ_m=0.5的冷水中，Ra=10⁴，Re=150时旋转系统强化传热效果最显著，此时的$\left\langle\overline{\kappa_{\mathrm{eqi}}}\right\rangle_t$是自然对流时的4.88倍。而当Ra增大时，随着浮力作用增强离心作用效果减弱，旋转强化传热的效果被削弱。图 8(c)展示了Re=100时不同Ra情况系统整体传热速率随Θ_m的变化。如图所示，在较高Ra条件下，浮力作用主导流动，受冷水的密度倒置特性影响，系统传热速率随Θ_m的增加先减小后增大，并在Θ_m=0.4和Θ_m=0.5时出现系统的传热低值。而当Ra=5×10⁴时，离心力主导流动，不同Θ_m下冷水系统的整体传热速率接近。图 8(d)进一步展示了Ra和Re不同时TC流动与自然对流传热速率的比值随Θ_m的变化，Re越大强化传热的效果越明显，当Θ_m=0.4和Θ_m=0.5时系统整体传热的增强幅度远大于其余密度倒置参数情况，在本文考察的参数范围内Θ_m=0.4时旋转的传热强化效果最为突出。

3 结论

本文采用三维数值模拟方法研究10⁴≤Ra≤10⁶范围内不同密度倒置参数的冷水在静止竖直环形腔内的自然对流(Re=0)和Re=30、50、100和150时的TC流动。重点关注参数空间中的流动特征以及旋转和浮力共同作用下的流态演化，分析控制参数变化对冷水传热特征的影响。主要结论如下：

1) 当Ra≥10⁵时，轴对称假设不适用，三维数值模拟得到的流动和传热结果与轴对称假设下得到的相应结果差异明显。随着Ra的增加，轴对称流态发展为非轴对称流态，流态的复杂度不断提高，系统整体传热也逐渐由稳态传热发展成混沌振荡传热。

2) 随着内圆柱转速增加，离心作用增强，流动逐步发展为稳态泰勒涡流，在此过程中观察到局部振荡的特殊流态。当Θ_m较小时，在上端面附近出现局部流场振荡，当Θ_m较大时，在下端面附近出现局部流场振荡。

3) 受到密度极值的影响，冷水流动与常规OB流体的流动特征有明显差异。在自然对流和内圆柱转速较低时，流动呈现径向分层的特征，出现bi-CoRV流动、bi-CoRWV流动和bi-SPI-p。较高转速时，随着Ra的变化SPI-n和SPI-p均会出现，且在一定Θ_m和Ra范围出现特殊流态SPI-r。

4) 在内圆柱高转速的情况下，随着Ra增加流态出现明显变化，使得系统整体传热速率呈现非单调变化趋势。旋转引起的离心作用改变了冷水的流动形态，极大地提高了系统的整体传热性能，且冷水的密度倒置特性越显著，对旋转的强化传热作用越敏感。