月球作为地球的卫星,一直受到各界科学家的关注。由于航天技术的进步,人们已经实现多次登月活动。在美国Apollo多次探月计划中,人类通过各种技术手段获取月球上空及表面的观测数据,采集月壤和月岩样品,有助于人们研究月球表面及其内部温度的时空演化特征,进而研究与月球热状态有关的月震活动性。
阿波罗登月计划对月球的重力场、电场、磁场进行了全面探测,并布设相当数量的月震仪器得到了相对全面的月震观测数据。根据前人对Apollo12、14、15、16、17的研究统计,截至2018年,长周期月震仪共探测到13 058次月震事件,其中深源月震7 083次(深度大约在700~1 200 km范围),深度大概几十到200 km范围内的月震28次,陨石撞击1 743次,热事件555次[1-2]。Duennebier和Sutton[3]认为,月表热事件多数震级较小、震源较浅,这些月震是由于月表日周期温度变化导致的热应力引起的热月震。有学者利用新的模式识别算法对Apollo17号记录的时长为8.3个月的月震事件进行分析,发现它们的发生与日出日落时间有一定的相关性,认为上述月震事件的物理解释可能是热驱动[3-4]。
一般认为,由于月球浅表受到太阳辐射周期性变化导致温度升降和热应力挤压-拉伸的周期性变化,从而导致月球发生热事件月震[3, 5]。因此,热事件月震的研究需要对月球表面温度的时空分布有更定量的了解。Apollo15的钻孔温度探测数据表明,月表该处最高温度为374 K,最低温度为92 K,而Apollo17着陆点测得月表最高温度为384 K,最低温度为102 K[6-7]。由于太阳辐射作用,月球表面温度与纬度相关,赤道的温度在满月时大概为390 K,而月夜期间,月球不受到太阳辐射,温度下降到100 K左右[8-9]。
月球表面大气稀薄,月表温度场基本上不受空气对流的影响。总体而言,月球的温度场主要有3个能量来源:一个是白天太阳光照的热量,一个是来自月幔的热量,最后一个就是地球对月球辐射所产生的热量输入[10]。对于月球表面而言,温度场的时空变化基本不受来自月幔的热量影响,而起重要影响的因素就是向内吸收的太阳辐射和向外释放的黑体辐射。月球的自转存在29.5 d的自转周期,在白昼条件下,月球表面的总热量来源主要为太阳光照与月表黑体辐射的热量之差,在夜晚条件下,月表只存在月表向外的黑体辐射。月球表面接收的太阳辐射量呈周期性变化,因此,月表温度也随着月球日周期性变化。
月球不同区域表面存在不同厚度的月壤,而月壤的热导率远低于月岩,月壤厚度对月球表面附近的温度的时空分布影响很大。Mitchell和Pater[11]分析了不同深度下的温度变化因素,温度高于350 K时,热辐射对月球浅层温度变化影响起主导作用,而在下层的固体岩石中,热传导起主导作用。在此基础上,Vasavada等[12]建立了对应的双层模型,认为月球表面温度在白昼时主要依赖太阳光照,日落后,月球表面失去热量来源,月表温度迅速下降。综合目前的研究,月球上大部分区域的月壤厚度约为几米,在月海区一般为3~5 m,而月球高地月壤厚度可能达到10 m[13-14]。Hayne等[15]对月壤特征厚度分布进行统计分析,得出月壤特征厚度的分布呈现非对称性的概率分布,在0~3 cm特征厚度范围内的月壤区域相对较少,而月壤特征厚度的最概然值约为7 cm。因此可以认为,月壤平均特征厚度可选取5 cm作为典型值。
目前针对月表温度变化的研究多为基于均匀介质模型进行分析,对温度场的演化进行研究[12, 16-17],或是基于Apollo样本以及近似模拟材料,对月球表面月壤风化层性质进行探究[15, 18]。而对温度变化引起的热应力变化更是缺乏深入的定量研究。实际上,月壤材料相对于月球基岩,热力学性质存在相当大的差异。根据月球波速结构的研究结果,月壤相对于月球基岩来说,月表介质的弹性波波速仅为深部的1/10[19],而月壤相对松散,孔隙度较高,因而导热率只有基岩导热率的1/1 000[10]。月表不同区域月壤厚度存在明显的差异[15, 17-18]。因此,研究月表温度场以及热驱动的热月震,需要对月壤的特征厚度和热力学参数有更定量的认识。本文利用自主研发的二维热弹性耦合有限元程序,以温度变化幅度最大的月球赤道区域为例,定量研究月球浅表的温度、垂直位移及热应力的时空分布,分析月壤特征厚度对温度、位移及热应力演化的影响,进而探讨月表附近热事件的动力学成因。
1 模型与方法本文不考虑来自月幔的热量,只考虑月表向内吸收的太阳光照热量和向外释放的黑体辐射热量。根据观测和模拟计算,月表温度变化会呈现出29.5 d的周期性[16, 20]。建立二维热弹性耦合有限元模型,考虑月壤的不同特征厚度及热力学参数随深度、温度变化的非线性,研究4个完整的月球日月表月壤的温度、位移和热应力的时空变化。相关的热力学参数的理论公式如下。
Hayne等[15]根据行星数据系统的研究结果,给出月壤密度模型
| $\rho(z)=\rho_{\mathrm{d}}-\left(\rho_{\mathrm{d}}-\rho_{\mathrm{s}}\right) \mathrm{e}^{-\frac{z}{H}} .$ | (1) |
其中:ρ(z)表示随深度变化的月壤密度,ρd表示在月壤底部处的密度,ρs表示月壤表面密度,z表示深度,H表示月壤特征厚度。
Schreiner等[18]利用Apollo计划带回的样本数据,对月表风化层的性质做了回归分析,并给出比热的拟合公式
| $C_p(T)=c_0+c_1 T+c_2 T^2+\cdots+c_N T^N .$ | (2) |
其中:Cp(T)表示热容随温度变化函数,T表示温度,c0, c1, …, cN表示拟合公式的比热系数。
根据实验数据,热导率与温度密度存在相关函数关系,得出以下公式[11, 15]:
| $\kappa=\kappa_{\mathrm{c}}\left[1+\chi\left(\frac{T}{350}\right)^3\right] \text {, }$ | (3) |
| $\kappa_{\mathrm{c}}=\kappa_{\mathrm{d}}-\left(\kappa_{\mathrm{d}}-\kappa_{\mathrm{s}}\right) \frac{\rho_{\mathrm{d}}-\rho}{\rho_{\mathrm{d}}-\rho_{\mathrm{s}}} .$ | (4) |
其中:κ为月壤的热导率,κc是与深度相关的热导率系数,κs和κd分别表示月壤表面和底部的热导率,ρs和ρd表示月壤表面和底部的密度,χ表示辐射热导率系数,T为月壤温度。
本文中,ρs=1 100 kg/m3,ρd=1 800 kg/m3,κs= 7.4×10-4 W·m-1·K-1,κd=3.4×10-3 W·m-1·K-1,χ=2.7[17]。
月表太阳吸收热量的计算公式[21]如下
| $Q_{\mathrm{S}}=(1-A) F(t) .$ | (5) |
其中:QS为月表吸收太阳光照的热量,A为月表太阳光反射率,F(t)为月表太阳光入射热量。
本文选取月表太阳反照率经验公式[15, 22-23],此公式已得到检验:
| $A(\theta)=A_0+a\left(\frac{\theta}{{\rm{ \mathsf{ π} }} / 4}\right)^3+b\left(\frac{\theta}{{\rm{ \mathsf{ π} }} / 2}\right)^8 .$ | (6) |
其中:A(θ)表示月表太阳反射率,θ表示太阳入射角,以弧度为单位;A0为反照率拟合基数;a、b均为拟合系数。本文采用A0=0.12,a=0.06,b=0.25[17]。
月表太阳光入射热量F(t)的计算公式[17]如下
| $\begin{gathered} F(t)= \\ \left\{\begin{array}{cc} \frac{S_0}{R_{A U}^2}\left(\sin \varPhi {\sin \delta+\cos \varPhi \cos \delta \cos h), }\right. & \cos h \geqslant 0 \\ 0, & \cos h<0 \end{array}\right.. \end{gathered}$ | (7) |
其中:S0为太阳常数,RAU表示太阳和月球间的距离,Φ表示纬度,δ为太阳偏角,h为与时间有关的时间角,h=2πt/P,t为时间,P为月球日周期。本文中以赤道地区为例,Φ=0°,δ=0°,S0=1 361 W/m2,RAU=1.0[17]。
本文使用Stefan-Boltzmann定律描述月球表面向外辐射的热量QT
| $Q_{\mathrm{T}}=\varepsilon \sigma T^4 \text {. }$ | (8) |
其中:ε表示物体发射率,σ表示Stefan-Boltzmann常数,T表示温度。本文中,ε=0.95,σ=5.67×10-8 W/(m2·K4)[17]。
热应力是由于物体在存在温度差的时候,温度的差异性分布会导致物体内部存在一定的局部性膨胀或收缩现象,温度的平衡过程会产生一定的热应力。对于月壤弹性体而言,温度演化公式[17]如下
| $\rho C_p \frac{\partial T}{\partial t}=\nabla \cdot(\kappa \nabla T)+Q.$ | (9) |
其中:ρ,Cp,κ,Q分别为月壤的密度、比热、热导率和热生成率。
月壤弹性体的应力平衡方程为
| $\sigma_{i j, j}+f_i=0 .$ | (10) |
弹性本构关系为
| $\boldsymbol{\sigma}=[\boldsymbol{D}]\left(\boldsymbol{\varepsilon}-\boldsymbol{\varepsilon}_\alpha\right) .$ | (11) |
其中:σ和ε分别表示应力和应变的列向量形式,εα表示热应变,[D]为弹性矩阵。弹性矩阵表示方法如下
| $[\boldsymbol{D}]=\left[\begin{array}{cccccc} \frac{E(1-\nu)}{(1+\nu)(1-2 \nu)} & \frac{E \nu}{(1+\nu)(1-2 \nu)} & \frac{E \nu}{(1+\nu)(1-2 \nu)} & 0 & 0 & 0 \\ \frac{E \nu}{(1+\nu)(1-2 \nu)} & \frac{E(1-\nu)}{(1+\nu)(1-2 \nu)} & \frac{E \nu}{(1+\nu)(1-2 \nu)} & 0 & 0 & 0 \\ \frac{E \nu}{(1+\nu)(1-2 \nu)} & \frac{E \nu}{(1+\nu)(1-2 \nu)} & \frac{E(1-\nu)}{(1+\nu)(1-2 \nu)} & 0 & 0 & 0 \\ 0 & 0 & 0 & 2 G & 0 & 0 \\ 0 & 0 & 0 & 0 & 2 G & 0 \\ 0 & 0 & 0 & 0 & 0 & 2 G \end{array}\right] .$ | (12) |
其中:E,ν,G分别为杨氏模量、泊松比和剪切模量。
热应变可以表示为
| $\boldsymbol{\varepsilon}_\alpha=\left[\begin{array}{c} \alpha \Delta T \\ \alpha \Delta T \\ \alpha \Delta T \\ 0 \\ 0 \\ 0 \end{array}\right].$ | (13) |
其中:α为热膨胀系数,ΔT为相对于初始温度的温度变化。
所以,二维平面应变热应力本构方程如下
| $\begin{aligned} {\left[\begin{array}{l} \sigma_{11} \\ \sigma_{22} \\ \sigma_{12} \end{array}\right]=} & {\left[\begin{array}{ccc} \frac{E(1-\nu)}{(1+\nu)(1-2 \nu)} & \frac{E \nu}{(1+\nu)(1-2 \nu)} & 0 \\ \frac{E \nu}{(1+\nu)(1-2 \nu)} & \frac{E(1-\nu)}{(1+\nu)(1-2 \nu)} & 0 \\ 0 & 0 & 2 G \end{array}\right] } \\ & {\left[\begin{array}{l} \varepsilon_{11} \\ \varepsilon_{22} \\ \varepsilon_{12} \end{array}\right]-\left[\begin{array}{c} \frac{E}{(1-2 \nu)} \alpha \Delta T \\ \frac{E}{(1-2 \nu)} \alpha \Delta T \\ 0 \end{array}\right] . } \end{aligned}$ | (14) |
在有限元计算中,边界条件是计算的一个重要因素。本文存在3个物理场,其一为温度场,左边界、右边界、下边界为绝热边界,上边界给定边界的热流边界条件,具体表示如下
| $Q_0=Q_{\mathrm{S}}-Q_{\mathrm{T}} .$ | (15) |
其中:QS、QT的表达式见式(5)和式(8)。
另2个物理场为位移场、应力场,其中左右边界水平方向上位移约束为0,垂直方向上不做约束;下边界垂直方向上位移约束为0,水平方向位移不做约束;上表面自由。
2 有限元模型的设计为探究月表附近热事件的动力学机制,本文采用热弹性有限元程序,建立了二维月壤剖面模型,水平0.1 m,深度1 m,水平网格尺寸为2 mm,0.2 m以浅的垂直网格尺寸为1 mm,0.2 m以下的垂直网格尺寸为4 mm。采用结构化四边形网格,共有20 451个有限元节点,20 000个四边形单元。分别设计了4个不同的有限元模型,其月壤特征厚度H分别为0、2、5、7 cm,其中月壤特征厚度为零的模型表示密度ρ取为底部密度ρd、热传导率κc取为底部热导率κd。其余的几何、材料、初始条件、边界条件一致。初始温度的分布情况对月球浅表温度场数值模拟的影响很大。廖翼[24]研究不同的初始温度分布(均匀条件或者指数条件)对月表附近温度场模拟计算的收敛性的影响,发现采用300 K的均匀初始温度需要120个月球自转周期才能达到计算稳定。本文采用月壤均匀初始温度为255 K,模型底部温度为255 K,表面采用月表太阳吸收热量Qs和月球表面向外辐射的热量QT相叠加的热流边界条件,两个侧面是无热流边界条件。对于位移场,月表自由,两个侧面和底面法向位移约束为零,切向位移自由。应力的计算采用式(11)。
本文材料模型选取见表 1。
|
|
表 1 月壤材料参数 Table 1 Lunar soil material parameters |
一个完整的月球日约为29.5个地球日。为了保证非线性计算收敛性以及耦合场计算精度,本文选取177 s为计算步长,相当于月球的0.1 min,每60个计算时间步存储1次计算结果,相当于月球上的每6 min存储1次计算结果。4个有限元模型的起算时间均为月球上的正午12:00,总共的计算时间为1.019 52×107 s,相当于计算4个完整的月球日。为提高计算效率,采用并行程序,利用9个计算核数,计算不同月壤特征厚度的4个模型的温度、位移和热应力场。
3 模拟结果选取月壤特征厚度为2 cm的有限元模型为参考模型,首先给出参考模型的温度、位移和热应力的计算结果。在太阳热辐射吸热和月球本身热辐射放热的共同作用下,月球表面及浅表的温度、位移和应力都呈现周期性的变化。对于我们的二维模型而言,深度方向是1 m,在垂直方向上,月表是自由的,月壤因温度变化将自由伸缩,没有约束力,因此理论上,垂直正应力为零。由于月表非线性的热流边界条件,有限元模拟得到的垂直正应力在月表附近可能会存在一定的数值误差,并随深度迅速衰减到零,故本文不考虑垂直正应力的影响。
图 1为深度分别为0,0.1,0.5,1,5,10,50 cm温度在4个完整的月球日和第4个月球日内随时间的变化曲线图。图 1(a)和1(b)的起始时间是正午12:00(下同)。除第1个月球日受初始场影响以外,其余3个月球日,月表及不同深度的温度,均呈现一定的周期性变化(图 1(a))。月表(图 1中的红线)在1个完整的月球日(以第4个完整的月球日为例,横坐标为72~96月球小时,其中横坐标72和96刚好对应月球上的正午12:00),正午12点温度达最大值384.85 K,早上6点温度达最小值100.13 K。从正午12:00到第2天的早上06:00,月表温度随时间都是降低的,其中白天的12:00(横坐标72)到18:00(横坐标78),温度从极大值开始急剧下降,18:00(横坐标为78)到第2天早上06:00(横坐标为90),温度缓慢下降,到06:00达到极小值。从第2天早上06:00(横坐标为90)到第2天正午12:00(横坐标为96),温度从极小值急剧升高到极大值,此过程与之前的12:00到18:00的过程刚好相反(图 1(b))。
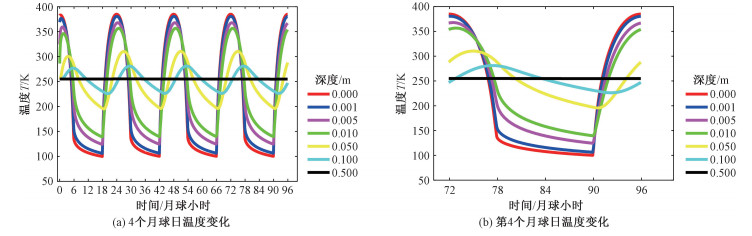
|
Download:
|
| 图 1 2 cm特征厚度月壤参考模型,不同深度下月壤温度随时间变化曲线图 Fig. 1 Curves of lunar soil temperature with time at different depths (Reference model of lunar soil with characteristic thickness of 2 cm) | |
月表之下0.1,0.5,1,5,10,50 cm的温度随时间的演化曲线,与月表的有一定的相似性,深度越大,温度曲线的变化幅度逐渐指数式减少。深度为50 cm时,温度基本不随时间变化。与此同时,温度的极大值出现比地表位相滞后,深度越深,极大值越往后推迟,0.1,0.5,1,5,10 cm的温度极大值和出现时间分别为:(0.1 cm, 380.53 K,12:12)、(0.5 cm,367.75 K,12:30)、(1 cm,356.63 K,12:54)、(5 cm,310.33 K,15:00)、(10 cm,281.09 K,17:30)。温度的极小值在1 cm以前依然是在06:00出现,5 cm以下极小值不在06:00出现,而是有所延迟(5 cm,195.70 K,06:36)、(10 cm,226.21 K,08:18)(图 1(b))。Turcotte和Schubert[29]给出了地表单一频率周期性随时间余弦分布的温度边界引起的温度幅值随深度的指数衰减和相位随深度的延迟的解析解,表明温度幅值随深度指数式减小,周期大的低频成分衰减较慢,周期小的高频成分衰减较快。本文的月表温度含有多种频率成分,因此,其温度随深度的衰减和相位延迟比单一频率的解析解结果要更复杂一些。
图 2给出不同深度,参考模型的垂直位移随时间或温度的变化曲线,同样呈现周期性变化(图 2(a))。垂直位移大于零代表抬升,小于零代表下降。以模拟的第4个月球日(同上)为例,月表的垂直位移变化范围最大,深度越深,垂直位移的变化范围越小,50 cm深度处的垂直位移几乎为零(图 2(b))。月表垂直位移极大值也呈现位相差异(图 2(b))。经过1个月球日的热胀冷缩,不同深度的垂直位移和温度的曲线基本是大小不一的封闭闭环(图 2(c)),由于月表总位移是不同深度不同温度热胀冷缩变化量的积分求和,所以呈现的深度衰减和位相滞后形式更为复杂。
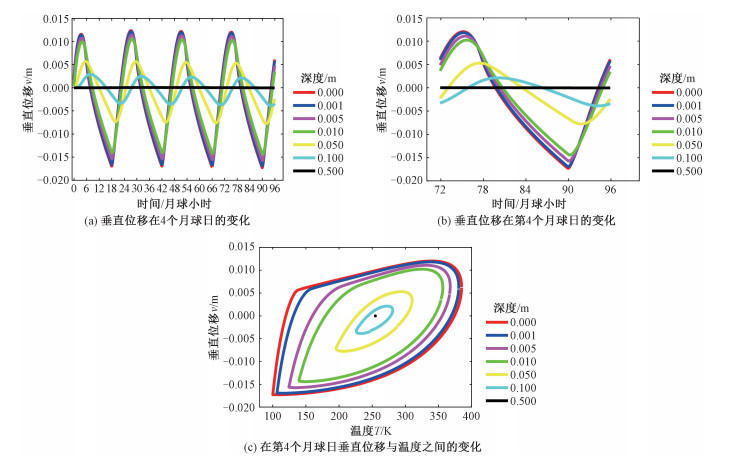
|
Download:
|
| 图 2 2 cm特征厚度月壤参考模型,不同深度下月壤垂直位移随时间或温度的曲线图 Fig. 2 Curves of vertical displacement of lunar soil with time or temperature at different depths (Reference model of lunar soil with characteristic thickness of 2 cm) | |
图 3给出不同深度,参考模型的水平正应力随时间或温度的变化曲线,同样呈现周期性变化(图 3(a))。水平正应力大于零表示拉张,小于零代表挤压。以模拟的第4个地球日(同上)为例(图 3(b)),月表(红线)的水平正应力的变化范围最大,极值及时刻如下:(0 cm,2.066 MPa,06:00),(0 cm,-1.731 MPa,12:00),(0.1 cm,1.982 MPa,06:00),(0.1 cm,-1.674 MPa,12:12),(0.5 cm,1.742 MPa,06:00),(0.5 cm,-1.503 MPa,12:30),(1 cm,1.541 MPa,06:00),(1 cm,-1.355 MPa,12:54),(5 cm,0.791 MPa,06:36),(5 cm,-0.738 MPa,15:00),(10 cm,0.383 MPa,08:18),(10 cm,-0.348 MPa,17:30),其中正值表示拉应力极大值,负值为压应力的极值(图 3(b))。月表水平正应力拉升的最大值出现在06:00,值为2.066 MPa;月表水平正应力挤压的最大值出现在12:00,值为-1.731 MPa。0~0.5 m深度,水平正应力也是周期性拉压的(图 3(b))。值得注意的是,18:00左右,水平正应力的变化最大,由压应力迅速地变为较大的压应力,然后经过晚上的12 h,拉应力缓慢增长到早上06:00的极大值(图 3(b))。经过1个月球日的热胀冷缩,不同深度的水平正应力和温度的曲线基本是长短不一的线段,月表对应的线段最长,50 cm深度对应的线段几乎缩为1个点。高温代表压缩,低温代表拉张,两者是线性关系,温度可以作为水平正应力的指示器(图 3(c))。如果考虑月表附近的拉应力破坏的话,18:00左右是拉应力增长最快的时刻,而早上06:00左右是拉应力最大的时刻,都是值得关注的。
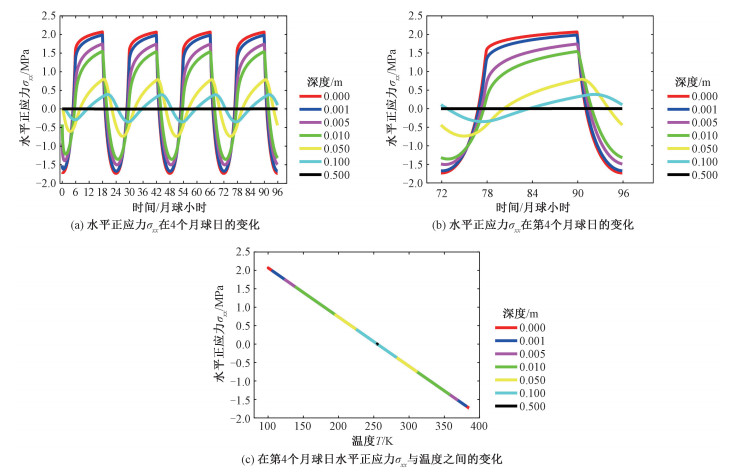
|
Download:
|
| 图 3 2 cm特征厚度月壤参考模型,不同深度下月壤水平正应力σxx在4个月球日随时间变化曲线图 Fig. 3 Curves of horizontal normal stress σxx of lunar soil with time in four lunar days at different depths (Reference model of lunar soil with characteristic thickness of 2 cm) | |
图 4为2 cm厚月壤参考模型模拟的第4个月球日(同上)不同时刻(每2个月球小时)温度随深度变化曲线图。可以看出温度主要在30 cm以浅的深度剧烈变化,变化范围约为100.13~384.85 K,50 cm深度以下温度基本不受月表影响,保持不变,约为255 K。综合来看,08:00到16:00是白天,月表有太阳光照射接收热量,温度较高,其中12:00的月表温度最高。18:00到06:00是夜晚,月表没有太阳光照射不接收热量,温度较低,其中18:00左右温度下降最快,06:00的月表温度最低。

|
Download:
|
| 图 4 2 cm特征厚度月壤参考模型,不同时间温度随垂直坐标的变化曲线图 Fig. 4 Curves of temperature with vertical coordinates for different time periods (Reference model of 2 cm characteristic thickness lunar soil) | |
图 5为2 cm厚月壤参考模型模拟的第4个月球日(同上)不同时刻(每2个月球小时)水平正应力随深度变化曲线图。可以看出水平正应力主要在30 cm以浅的深度剧烈变化,水平正应力的变化范围约为-1.731~2.066 MPa,既有拉应力,也有压应力,拉应力的极大值要大于压应力的极大值。50 cm深度以下水平正应力基本不受月表的影响,几乎为零。综合来看,08:00到16:00是白天,月表有太阳光照射接收热量,月表水平正应力是压应力,其中12:00的月表的水平压应力最大(图 5(a))。18:00到次日06:00是夜晚,月表没有太阳光照射不接收热量,月表水平正应力是拉应力,其中18:00左右拉应力增长最快,06:00的拉应力最大(图 5(b))。若将垂向坐标轴改为相应的温度轴,则无论是白天,还是夜晚,水平正应力与温度都是在一条直线上,两者是线性关系,温度可以作为水平正应力的指示器(图 5(c)、5(d))。
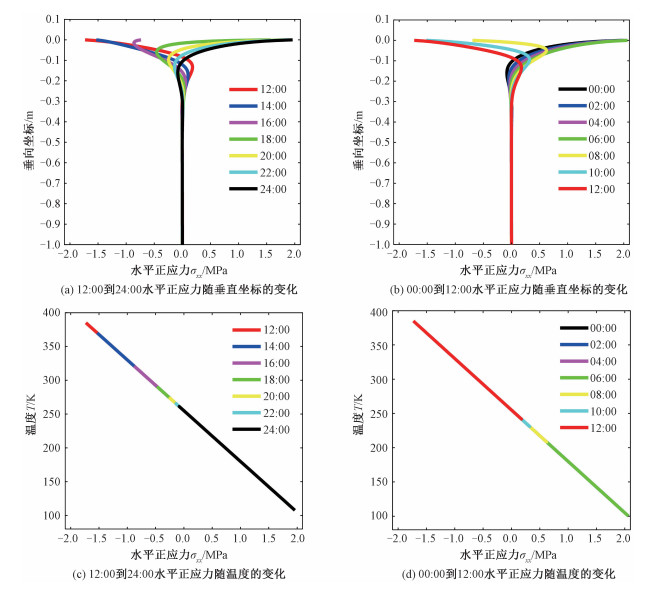
|
Download:
|
| 图 5 2 cm特征厚度月壤参考模型,不同时间水平正应力σxx随垂直坐标或温度的变化曲线图 Fig. 5 Curves of horizontal normal stress σxx with vertical coordinate or temperature at different time (Reference model of lunar soil with characteristic thickness of 2 cm) | |
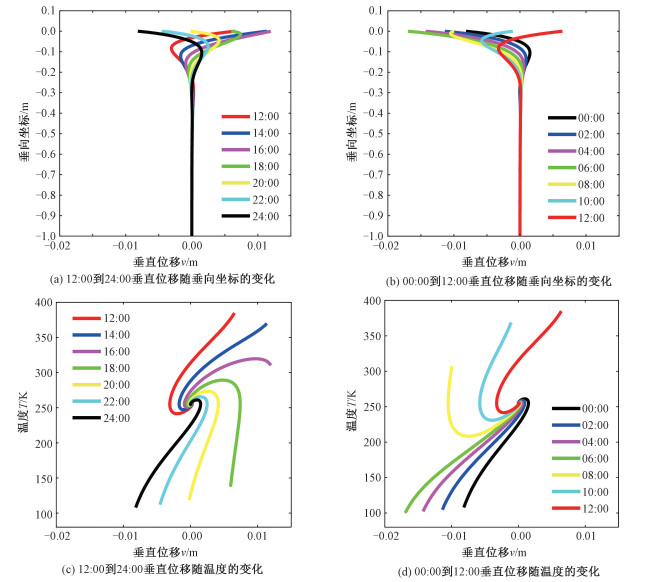
图 6为2 cm厚月壤参考模型模拟的第4个月球日不同时刻(每2个月球小时)垂直位移随深度变化曲线图。可以看出垂直位移主要在30 cm以浅的深度剧烈变化,变化范围约为-0.017 0~0.012 0 m,既有抬升,也有下降,下降的极大值要大于抬升的极大值。50 cm深度以下垂直位移基本不受月表的影响,几乎为零。注意,与温度、水平正应力不同,月表的垂直位移的抬升、下降并不是跟白天和夜晚严格对应,而是有一定的延迟或滞后。从正午12:00,抬升量呈(12:00,0.006 3 m),(14:00,0.011 0 m),(16:00,0.011 6 m),(18:00,0.005 6 m)变化,均表示地表抬升(图 6(a))。而(20:00, -5.236 6e-04 m), (22:00, -0.004 9 m),(00:00,-0.008 5 m),(02:00,-0.011 7 m),(04:00,-0.014 6 m),(06:00,-0.017 3 m),(08:00,-0.010 3 m),(10:00,-0.001 4 m)变化,均表示地表下降(图 6(a)、6(b))。若将垂向坐标轴改为相应的温度轴,则无论是白天,还是夜晚,垂直位移与温度呈发散状分布,两者不是线性关系(图 6(c)、6(d))。
|
Download:
|
| 图 6 2 cm特征厚度月壤参考模型,不同时间垂直位移v随深度变化曲线图 Fig. 6 Curves of vertical displacement v with depth at different time (Reference model of lunar soil with characteristic thickness of 2 cm) | |
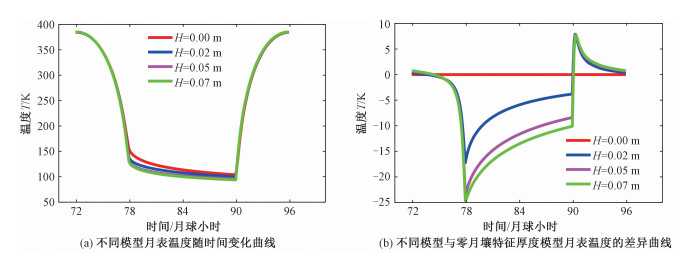
图 7给出不同月壤特征厚度对月表温度演化的影响。可以看出,白天12:00—18:00(图 7横坐标72~78),06:00—12:00(图 7横坐标90~96),仅在06:00和18:00附近有较大差异,除此之外,在白天的时段,4条温度曲线几乎完全重合。而夜晚时段18:00—06:00(图 7横坐标78~90),月球接收不到太阳光照,只有月球向外辐射热量,而此时,不同厚度的风化层保温效应不同,也因此表现为不同的月壤特征厚度对温度的时间演化有影响。以模拟的第4个月球日(同上)为例,夜晚时段,在早上06:00时,4个模型的温度差异最大,分别为(0 cm,103.93 K),(2 cm,100.13 K),(5 cm,95.55 K),(7 cm,93.83 K)。
|
Download:
|
| 图 7 第4个月球日不同月壤特征厚度模型的月球表面温度随时间变化曲线(起始时间是12:00) Fig. 7 On the fourth lunar day, curves of lunar surface temperature with time under different lunar soil characteristic thickness models (the starting time is 12:00 at noon) | |
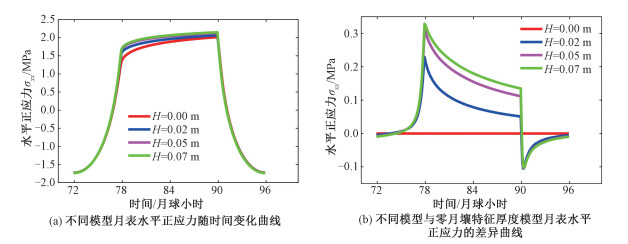
图 8给出不同月壤特征厚度对月表水平正应力演化的影响。可以看出,白天仅在06:00和18:00附近水平正应力有较大差异,除此之外,在白天的时段,4条曲线几乎完全重合。而夜晚时段18:00—06:00(图 7横坐标78~90),水平正应力与温度类似,与月壤风化层厚度密切相关(图 8(a)、图 8(b))。
|
Download:
|
| 图 8 不同月壤特征厚度模型的月球表面水平正应力随时间变化曲线(起始时间是12:00) Fig. 8 Time varying curves of horizontal normal stress on the lunar surface of different lunar soil characteristic thickness models (the starting time is 12:00 at noon) | |
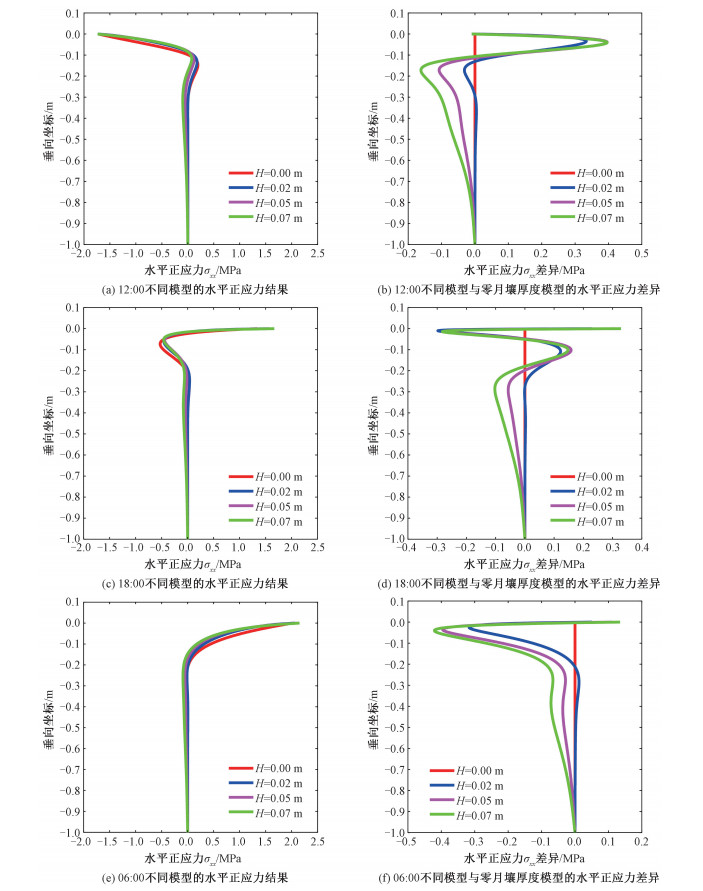
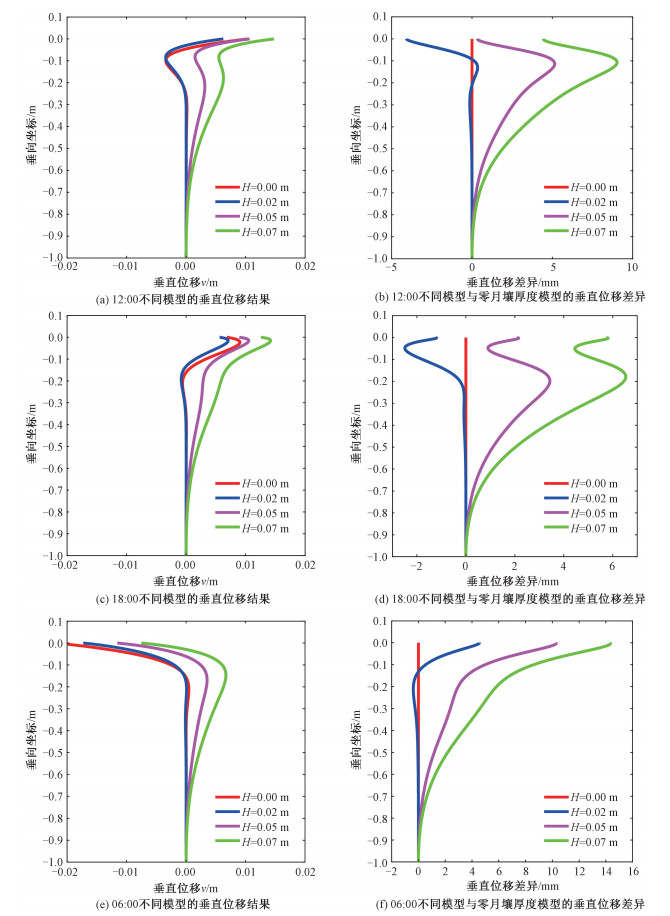
图 9、10、11分别给出不同月壤特征厚度模型在月球时间12:00、18:00、06:00时温度、水平正应力和垂直位移及其与零特征厚度模型差异随深度变化曲线。可以看出,不同特征厚度模型的温度、水平正应力和垂直位移随深度都有较为明显的变化,尤其是在较浅的月表附近。

|
Download:
|
| 图 9 不同月壤特征厚度模型的温度随深度的变化 Fig. 9 Curves of temperature with depth of different lunar soil characteristic thickness models | |
|
Download:
|
| 图 10 不同月壤特征厚度模型的水平正应力随深度的变化 Fig. 10 Curves of horizontal normal stress with depth of different lunar soil characteristic thickness models | |
|
Download:
|
| 图 11 不同月壤特征厚度模型的垂直位移随深度的变化 Fig. 11 Variation curve of vertical displacement with depth by different models | |
在正午12:00,10 cm以浅的区域,月壤特征厚度越大,相对零特征厚度模型,温度越低,在5 cm深度附近差异可达-30 K(图 9(a)、图 9(b)),水平正应力的差异越大,在5 cm深度附近差异可达+0.4 MPa(图 10(a)、图 10(b)),而在10 cm以下的深度,温度、水平正应力呈现相反的变化趋势。在正午12:00,月壤特征厚度越大,相对零特征厚度模型,垂直位移增长越大,在10 cm深度处的最大差异接近+10 mm(图 11(a)、图 11(b))。
在傍晚18:00,10 cm以浅的区域,月壤特征厚度越大,相对零特征厚度模型,温度越低,在5 cm深度附近温度差异量可达+20 K(图 9(c)、图 9(d)),水平正应力的差异越大,在5 cm深度附近差异可达-0.3 MPa左右(图 10(c)、图 10(d)),而在10 cm以下的深度,温度、水平正应力呈现相反的变化趋势。在傍晚18:00,月壤特征厚度越大,相对零特征厚度模型,垂直位移增长越大,在20 cm深度处的最大差异接近+6 mm(图 11(c)、图 11(d))。
在早上06:00,10 cm以浅的区域,月壤特征厚度越大,相对零特征厚度模型,温度越低,在5 cm深度附近温度差异量可达+30 K(图 9(e)、图 9(f)),水平正应力的差异越大,在5 cm深度附近差异可达-0.4 MPa(图 10(e)、图 10(f))。在早上06:00,月壤特征厚度越大,相对零特征厚度模型,垂直位移增长越大,在月表处的最大差异接近+14 mm(图 11(e)、图 11(f))。
4 讨论1) 2 cm月壤特征厚度的参考模型计算结果,月表温度最大值为384.85 K,刚好是12:00,温度最小值为100.14 K,刚好是06:00,代表的是月表赤道附近的温度范围。Apollo15的钻孔温度探测数据表明,月表该处最高温度为374 K,最低温度为92 K,而Apollo17着陆点测得月表最高温度为384 K,最低温度为102 K[6-7]。赤道的温度在满月时温度大概为390 K,而月夜期间,月球不受到太阳辐射,温度下降到100 K左右[8-9]。我们数值模拟的结果与观测结果基本一致。
2) 月壤上下边界存在一定的温度差,且由碎屑为构成成分的月壤孔隙度高且变形能力相对下层基岩而言较弱,因而使得月壤层内本身应力差较小。而如果月壤厚度较大,月表热量难以及时传导到月球深部基岩,进而使得岩石温度变化较小。对应在热应力中,则表现为难以产生较大的热应力值,所以月壤较厚的区域热事件分布相对稀疏,数量较少;而对于较薄的月壤,温度相对而言易于传播,使得月球基岩的温度变化剧烈,产生较大的热应力,因而薄月壤区域容易发生较为密集的热事件[3]。月表温度急剧下降最快的时刻是18:00左右,对应的水平正应力是拉应力,而且增加最快。月表温度最低的时刻是06:00左右,对应的水平正应力是拉应力,而且此时的拉应力最大。18:00到第2天的06:00,水平正应力都是拉应力,而且是缓慢增长到最大的拉应力。因此,需要关注早晚6点左右的时刻,比较有利于发生月表附近的热事件。
3) 太阳照射的时段06:00—18:00,而且吸收热量与太阳的入射角有关,12:00的入射角为0°,此时月表温度达到极大值,06:00—12:00,入射角从90°逐渐变为0°,吸收的热量越来越大,温度迅速升高;12:00—18:00,入射角从0°逐渐变为90°,吸收的热量越来越小,温度迅速降低。18:00—06:00,夜晚,没有太阳照射,完全是月球向外的热辐射,温度继续降低,但是降温的速度比较缓慢。随着深度增加,温度差异逐渐减小,最终达到平均温度。对于不同厚度的月壤模型,月壤厚度越大对应的月表和月岩温度差异越大,这与前人的研究结果相符[25, 30]。这也与月球月壤的主要构成成分为碎屑相关,相对月岩来说导热能力较弱。
4) 月表垂直位移与月表温度、水平正应力的时间曲线有所不同,有一定的滞后性。换句话说,月表垂直位移相对于温度、水平正应力而言,有一个积分响应,有一个累积的过程。不同的月壤特征厚度,对于温度和正应力而言,在白天影响较小,夜晚有一定影响,06:00左右4个模型的差异最大。不同的月壤特征厚度,对于垂直位移而言,4个模型的差异对所有时段都有显著差别,更是体现垂直位移的时间滞后性和累积性。
5) 本文在月球浅表温度计算中没有考虑来自月幔的热流,因为50 cm以下深度的月热流密度实测值仅为20~40 mW/m2[31],而计算(第4个月球日)表明,08:00从月表向下传导的1 m深度平均热流密度为39 mW/m2,18:00从底部向月表传导的1 m深度平均热流密度可达87 mW/m2,月表 1 m深度范围内的平均热流差异也很大,甚至反向,模拟得到的热流密度与实测结果在数量级上一致。模拟结果还表明,08:00从月表向下传导的1 cm深度平均热流密度达3.7 W/m2,18:00从1 cm深度向月表传导的平均热流密度达7.2 W/m2,远远超过50 cm以下深度的月热流密度实测值20~40 mW/m2,说明来自月幔的热流对于月表附近的温度演化可以忽略不计[25]。
6) 本文建立的是二维模型,但材料参数和边界条件是一维的。通过这个简单的模型,验证了自主开发的热弹性有限元程序的正确性。月表附近的月岩跟月壤的热弹性参数有很大的区别,因此,二维模型,甚至三维模型是必要的,在月球观测和实验的最新数据的基础上,研究月壤与月岩在横向上和纵向上的差异性、月表地形的非均匀起伏和太阳光照吸收热量的时空变化不均匀性的影响,这也是未来进一步探究月表附近的热月震的重要方向之一。
5 结论本文利用热弹性耦合有限元并行程序对月表月壤特征厚度差异造成的温度、位移和热应力时空演化进行建模计算,得出以下结论:
1) 当月壤特征厚度为2 cm时,月表及50 cm以浅的月壤温度、垂直位移和水平正应力随时间成周期性变化,赤道地区温度在100~385 K之间变化,垂直位移在-0.017~0.012 m之间升降,水平正应力在-1.731~2.066 MPa之间压缩与拉张变化。这些周期性变化的外因在于月表太阳吸收热量Qs和月球表面向外辐射的热量QT相叠加的热流边界条件,同时月壤随深度、温度变化的热力学参数的非线性是其内因。
2) 下午到18:00日落时分,是月表温度下降最快的时刻,同时也是月表水平正应力从压应力转为张应力变化速率最快增加的时刻。06:00日出时分,是月表温度最低的时刻,同时也是月表水平拉应力最大的时刻。06:00日出后的时段,是月表温度增加最迅速的时段,也是月表水平应力从最大拉张应力迅速转变为压应力的时段。日落和日出的相近时间,可能是月表附近热事件或热月震相对集中的时刻。更精确的模拟,还应考虑月表地形的起伏和月表附近介质的横向不均匀性。
3) 月壤温度、垂直位移和水平正应力在月表以下较浅的深度变化较大。与零特征厚度模型相比,月壤特征厚度越大,无论是温度、水平正应力还是垂直位移,差异也越大,并且不同时段的差异还有所不同,表明月壤特征厚度的影响需要进一步的定量研究。
| [1] |
Nakamura Y. Farside deep moonquakes and deep interior of the Moon[J]. Journal of Geophysical Research: Planets, 2005, 110(E1): E01001. Doi:10.1029/2004je002332 |
| [2] |
Nakamura Y, Latham G, Dorman H J, et al. Passive seismic experiment, long period event catalog, final version (1969 day 202-1977 day 273, ALSEP stations 11, 12, 13, 14, 15, and 16)[R]. Institute for Geophysics, 1981. DOI: 10.15781/t2ff3mh78.
|
| [3] |
Duennebier F, Sutton G H. Thermal moonquakes[J]. Journal of Geophysical Research, 1974, 79(29): 4351-4363. Doi:10.1029/jb079i029p04351 |
| [4] |
Dimech J L, Knapmeyer-Endrun B, Phillips D, et al. Preliminary analysis of newly recovered Apollo 17 seismic data[J]. Results in Physics, 2017, 7: 4457-4458. Doi:10.1016/j.rinp.2017.11.029 |
| [5] |
赵娜. 月震特征及与地震的对比[J]. 空间科学学报, 2020, 40(2): 264-272. Doi:10.11728/cjss2020.02.264 |
| [6] |
Keihm S J, Peters K, Langseth M G, et al. Apollo 15 measurement of lunar surface brightness temperatures thermal conductivity of the upper 1 1/2 meters of regolith[J]. Earth and Planetary Science Letters, 1973, 19(3): 337-351. Doi:10.1016/0012-821X(73)90084-8 |
| [7] |
Heiken G, Vaniman D, French B. Bookreview: lunar sourcebook: a user's guide to the moon[J]. Sky & Telescope, 1991, 82: 498. Doi:10.5860/choice.29-3868 |
| [8] |
Criswell D R, Lindsay J F. Thermal moonquakes and booming dunes[C]//Abstracts of the Lunar and Planetary Science Conference: Houston, 1974.
|
| [9] |
欧阳自远. 月球科学概论[M]. 北京: 中国宇航出版社, 2005.
|
| [10] |
Lozano A. Development of a lunar regolith thermal energy storage model for a lunar outpost[D]. Luleå: Luleå University of Technology, 2016.
|
| [11] |
Mitchell D L, de Pater I. Microwave imaging of mercury's thermal emission at wavelengths from 0.3 to 20.5 cm[[J]. Icarus, 1994, 110(1): 2-32. Doi:10.1006/icar.1994.1105 |
| [12] |
Vasavada A R, Paige D A, Wood S E. Near-surface temperatures on mercury and the moon and the stability of polar ice deposits[J]. Icarus, 1999, 141(2): 179-193. Doi:10.1006/icar.1999.6175 |
| [13] |
Shkuratov Y G, Bondarenko N V. Regolith layer thickness mapping of the moon by radar and optical data[J]. Icarus, 2001, 149(2): 329-338. Doi:10.1006/icar.2000.6545 |
| [14] |
Fa W Z, Wieczorek M A. Regolith thickness over the lunar nearside: results from earth-based 70 cm Arecibo radar observations[J]. Icarus, 2012, 218(2): 771-787. Doi:10.1016/j.icarus.2012.01.010 |
| [15] |
Hayne P O, Bandfield J L, Siegler M A, et al. Global regolith thermophysical properties of the moon from the diviner lunar radiometer experiment[J]. Journal of Geophysical Research: Planets, 2017, 122(12): 2371-2400. Doi:10.1002/2017je005387 |
| [16] |
徐向华, 梁新刚, 任建勋. 月球表面热环境数值分析[J]. 宇航学报, 2006, 27(2): 153-156, 200. Doi:10.3321/j.issn:1000-1328.2006.02.001 |
| [17] |
任德鹏, 贾阳, 彭松. 月面热环境的反演研究[J]. 宇航学报, 2018, 39(4): 435-441. Doi:10.3873/j.issn.1000-1328.2018.04.010 |
| [18] |
Schreiner S S, Dominguez J A, Sibille L, et al. Thermophysical property models for lunar regolith[J]. Advances in Space Research, 2016, 57(5): 1209-1222. Doi:10.1016/j.asr.2015.12.035 |
| [19] |
Kovach R L, Watkins J S. The velocity structure of the lunar crust[J]. The Moon, 1973, 7(1/2): 63-75. Doi:10.1007/BF00578808 |
| [20] |
张翔, 张金海. 月震研究进展与展望[J]. 地球与行星物理论评, 2021, 52(4): 391-401. Doi:10.19975/j.dqyxx.2021-032 |
| [21] |
Liou K N, Liou K N. An Introduction to atmospheric radiation[M]. Amsterdam, Boston: Academic Press, 2002.
|
| [22] |
Keihm S J. Interpretation of the lunar microwave brightness temperature spectrum: feasibility of orbital heat flow mapping[J]. Icarus, 1984, 60(3): 568-589. Doi:10.1016/0019-1035(84)90165-9 |
| [23] |
Vasavada A R, Bandfield J L, Greenhagen B T, et al. Lunar equatorial surface temperatures and regolith properties from the Diviner Lunar Radiometer Experiment[J]. Journal of Geophysical Research: Planets, 2012, 117(E12): E00H18. Doi:10.1029/2011je003987 |
| [24] |
廖翼. 月球表面物理温度分布模型及数值计算[D]. 武汉: 华中科技大学, 2011.
|
| [25] |
Colwell J E, Batiste S, Horányi M, et al. Lunar surface: dust dynamics and regolith mechanics[J]. Reviews of Geophysics, 2007, 45(2): RG2006. Doi:10.1029/2005rg000184 |
| [26] |
Alshibli K A, Hasan A. Strength properties of JSC-1A lunar regolith simulant[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(5): 673-679. Doi:10.1061/(asce)gt.1943-5606.0000068 |
| [27] |
Ledlow M J, Zeilik M, Burns J O, et al. Subsurface emissions from Mercury: VLA radio observations at 2 and 6 centimeters[J]. The Astrophysical Journal Letters, 1992, 384: 640. Doi:10.1086/170906 |
| [28] |
Malla R B, Brown K M. Determination of temperature variation on lunar surface and subsurface for habitat analysis and design[J]. Acta Astronautica, 2015, 107: 196-207. Doi:10.1016/j.actaastro.2014.10.038 |
| [29] |
Turcotte D, Schubert G. Geodynamics[M]. 3th ed. Cambridge: Cambridge University Press, 2014.
|
| [30] |
占伟, 李斐. 月球内部构造研究综述[J]. 地球物理学进展, 2007, 22(3): 737-742. Doi:10.3969/j.issn.1004-2903.2007.03.012 |
| [31] |
Langseth M G, Keihm S J, Peters K. Revised lunar heat-flow values[C]//Lunar Science Conference. Houston, 1976: 3143-3171.
|
 2024, Vol. 41
2024, Vol. 41 


