2. 中国科学院工程热物理研究所, 北京 100190
2. Institute of Engineering Thermophysics, Chinese Academy of Sciences, Beijing 100190, China
航空发动机被誉为现代工业“皇冠上的明珠”,其发展水平是衡量一个国家科技水平重要标准之一[1]。与航空技术发达国家相比,我国发动机仍较落后,其中涉及的核心技术一直被“卡脖子”[2]。在发动机研发中,准确评估部件温度场具有重要意义。伴随着发动机性能不断提高,其热端部件工作温度逐渐升高,工作环境愈加恶劣。由材料热防护不当、热弯曲和热蠕动变形等引发的发动机故障问题逐渐不容忽视[3]。在对发动机进行换热优化设计以确保其安全运行时,准确评估热端部件温度场的重要性日益彰显。此外,叶顶间隙,即发动机转子叶片顶部与机匣间的径向间隙,作为发动机中一个重要参数,对其进行有效控制非常重要。间隙过小,叶片和机匣受热载荷作用变形时易相互碰撞,引起发动机振动,甚至损伤叶片;间隙过大,高温、高压气体泄漏过多,涡轮效率下降,影响发动机耗油率[4]。相关数据表明:间隙与叶高比增大1%,涡轮效率约下降1.2%,整机耗油率增加近2%[5]。因此,为控制叶顶间隙,需要准确评估发动机机匣和叶片等部件温度场。
在评估部件温度场时,部件间接触热阻的影响不容忽视。受工艺限制及安装维修的便利性,发动机各部件大多通过螺栓或榫头榫槽等非连续方式连接,如图 1所示。由于材料表面粗糙度的存在,实际接触面积较小使得界面产生附加热阻,当热流流过时,界面两侧会存在温差。对于发动机这种高热流密度场合,考虑连接部件间的接触热阻对准确预测其温度场显得尤为重要。特别地,对于像机匣法兰边等尺寸较小的关键部件,其导热热阻相对较小,接触热阻对部件温度场影响更不应忽视。

|
Download:
|
| 图 1 航空发动机部件间常见的两种连接方式 Fig. 1 Two common connection methods between aero-engine components | |
针对接触热阻问题,研究者最初从三方面进行理论分析:接触导热模型建立、表面形貌数学表征和接触点变形机制分析。较经典的有GW弹性[7]、CMY塑性[8]和Mikic[9]弹塑性接触模型。Greenwood和Williamson [7]指出实际接触面积与加载压力成正比。Mikic[9]给出判断表面形变方式的塑性指数、实际接触面积以及接触热阻理论关联式。随着计算机发展,接触热阻数值研究获得关注。Cui等[10]结合格子玻尔兹曼和有限差分法研究发现低压下接触热阻主要受材料热导率影响。Verma和Mazumder [11]使用尺度分辨直接数值模拟法给出接触热导与接触对数量的线性拟合公式。Dai等[12]用显微镜测量表面形貌并通过Abaqus完成接触物体变形和传热有限元计算,发现当界面温度小于350 ℃,热辐射对接触热阻的影响可忽略。
尽管接触热阻理论和数值研究得到一定发展,然而因其复杂性——涉及材料、传热、几何和力学等多学科交叉,现今仍没有一个统一理论能够很好地解释所有实验数据或普适的经验公式用以预测各种工况下接触热阻[13]。因此,到目前为止,最常见且较可靠方式依旧是凭借实验研究接触热阻。其实验测量方法按流过试件热流是否恒定分为:稳态法和瞬态法,详细介绍可参考文献[14]。稳态法因具有可靠性好、可操作性强和测量精度高等优点得到国内外学者青睐。表 1总结了不同材料、界面压力P和界面平均温度θ和粗糙度Ra等工况下接触热阻实验研究现状。Wahid等[15]研究真空环境接触热阻,结果表明RMS粗糙度高度和表面凸起斜率之比是影响接触热阻的重要参数。姬亚萌等[16]和Liu等[17]发现在较高压力时,γ-TiAl/2Cr12NiMoWV界面微凸体因发生弹塑性变形,其接触热阻减小幅度逐渐增大,而2Cr12NiMoWV/BH137则相反。Tang等[18]研究发动机材料接触热阻,研究表明热流方向对接触热阻影响较小。Zheng等[19]指出仅在界面添加最优厚度的C纤维,接触热阻才会明显减小。Xing等[20]发现在高温下接触热导随压力变化更明显。Dou等[21]研究空气环境接触热阻,结果表明粗糙度越大,接触热导随温度升高增加幅度越快。
|
|
表 1 接触热阻实验研究现状 Table 1 Experimental research status of thermal contact resistance |
鉴于接触热阻研究具有重要学术和工业应用价值,虽然常规材料的研究得到学者大量关注,但对发动机中材料的研究相对较少,特别是广泛用于涡轮叶片的新型DD5材料以及机匣的1Cr11Ni2W2MoV材料。其次,现有研究界面压力大多小于15 MPa,然而在发动机应用环境中压力高达200 MPa。由于低压下实际接触面积较小,接触间隙导热对界面热量传递起主导作用,而高压下实际接触面导热的影响逐渐加强并占主导,这导致高低压下接触热阻变化规律有所不同。已有实验台因大部分仅适用于低压工况而存在一定局限性,为测量更高压力接触热阻,需搭建具有更高标准和要求的实验系统。此外,值得说明的是,图 1中两种连接结构涉及界面压力非均分和非平面接触问题,对其中接触热阻直接研究较困难,且因结构复杂性,研究结果适用性有限。因此,本文提取两接触圆柱体这种最基本结构,对其在不同均匀界面压力和温度下接触热阻进行研究,从而为解决复杂实际问题奠定基础。
综上所述,本文基于发动机连接部件界面实际工况,根据稳态热流法搭建实验装置,测量DD5和1Cr11Ni2W2MoV材料接触热阻R,分析界面压力P和平均温度θ对其影响,得出接触热阻与两者经验关系式,本装置可测量界面最大200 MPa压力和最高300 ℃温度下的接触热阻。该研究可为发动机部件优化设计、叶顶间隙控制和材料热防护提供基础数据。
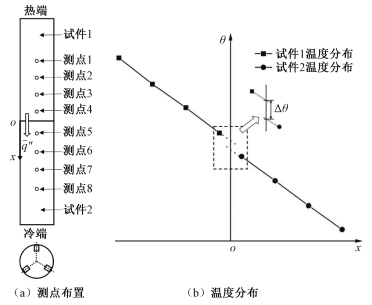
1 实验方法和系统装置 1.1 实验方法考虑图 2(a)中两接触圆柱试件1和2,在其两端和外壁面分别给定高温、低温和绝热边界条件。在温差的驱动下,热量从上向下传导,试件温度逐渐上升。由于试件外壁面保持绝热、温度场呈轴对称分布,当温度达到稳态时,其仅与轴向坐标x有关。根据圆柱坐标系下的一维热传导方程,任一x位置处热导率和温度梯度之积为常数,即热流密度为定值。当忽略材料热导率随温度变化,试件温度随x线性分布。
|
Download:
|
| 图 2 试件1和2测点布置和温度分布示意图 Fig. 2 Schematic diagram of layout of measuring points and temperature distribution on specimen 1 and 2 | |
在界面x=0处,因材料表面粗糙度的存在,实际接触面积较小,填充在间隙的空气热导率较低,当热流流过,界面会产生附加热阻,温度梯度会增加以维持热流密度恒定。所以,当将试件1和2线段温度向界面外插,会存在图 2(b)所示的温差Δθ。
因试件1和2温度θ随轴向坐标x线性变化,故有
| $\theta=w x+s.$ | (1) |
其中w和s表示试件1和2的温度梯度和在界面处温度。通过温度传感器获得不同xi处温度θi后,根据最小二乘法可求上述参数,进而可知界面温差Δθ和流过界面的平均热流密度q″,两者之比即为接触热阻R。
由于加载压力较大,界面压力可能分布不均匀从而给接触热阻测量带来不利影响。与现有文献仅布置1路测温点不同[18-19, 21],为减小这种影响,在系统装置中加实心钢球的同时(见图 3),还在每个试件上均匀布置3路测点(见图 2(a)),并将每个轴向x位置的测点温度取平均以更真实反映试件温度分布情况。布置3路测点还具有当实验中热电偶意外损坏导致某路数据缺失时,还可使用另外2路的优点。
|
Download:
|
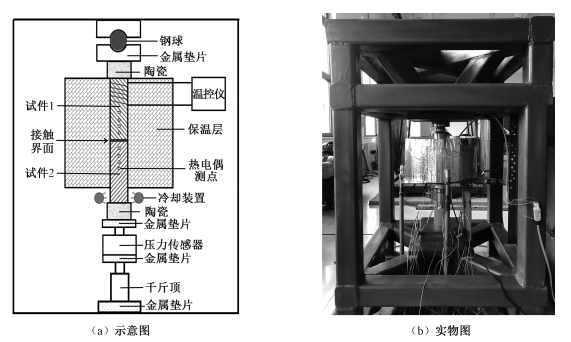
| 图 3 接触热阻测量实验系统 Fig. 3 Experimental system of measuring thermal contact resistance | |
基于上述方法,自主设计搭建如图 3所示接触热阻测量实验系统,图 3(a)为其示意图,3(b)为实物图。
该实验系统主要包含以下几部分:
1) 温控系统:加热装置位于图 3(a)中试件1顶端,其功率最大为3 300 W,加热温度最高为450 ℃。冷却装置位于试件2底端,使用空冷,压缩空气由BLT-20A/8螺杆压缩机提供。
2) 压力控制系统:两圆柱体接触界面压力通过JRCS-201型号千斤顶施加。其量程为200 kN,可满足发动机连接部件界面压力高达200 MPa实际需求。
3) 测量系统:通过LPJN1轮辐式压力传感器测量界面压力,其量程与千斤顶的一致,精度为0.5%。灵敏度高和稳定性好的J型热电偶与研华4118板卡相连以采集试件温度,热电偶使用前先放入恒温炉中进行校准,校准精度为0.3 ℃。此外,由于界面温度无法直接布置探头测量,采用界面平均温度θ表征其对接触热阻影响,其数值通过将试件1和2上测点温度线性外插到界面后取平均得到。
4) 保温系统:为减小系统热损,保温材料选常温热导率仅0.021 W/(m·K)的气凝胶,保温层厚度约180 mm。
试件1和2直径均为30 mm,长度分别为110和130 mm。因冷端所需空间比热端大,出于系统保温考虑,将试件2长度多加20 mm。两试件接触界面位于x=0 mm处,其测点布置方案及坐标如图 2(a)和表 2所示。其他2路测点布置与此一致,仅周向角相差120°。为减小测点对试件温度场影响,测点深度取5 mm,其直径与热电偶的相同为1 mm。热电偶插入其中后从试件2底部(即冷端)引出,紧接着缠绕一圈耐高温保温棉固定热电偶,随后缠绕剩余保温棉至所需厚度。
|
|
表 2 各测点x方向坐标 Table 2 Coordinate for every measuring point in x direction |
需要说明的是,本文研究DD5和1Cr11Ni2W2MoV材料接触热阻均指同种材料配对情况,即DD5与DD5和1Cr11Ni2W2MoV与1Cr11Ni2W2MoV间接触热阻,后文不再赘述。为便于比较,原则上应保证不同材料接触面粗糙度一致,但受磨床加工影响,将两材料表面粗糙度尽量控制在1.3~1.6 μm,其中DD5和1Cr11Ni2W2MoV材料接触面粗糙度分别为1.298和1.377 μm以及1.539和1.609 μm。此外,为方便比较后文结果,材料热导率和屈服强度列于表 3、表 4。常温下DD5和1Cr11Ni2W2MoV维氏硬度分别为3 234和3 204 MPa。DD5因是新型合金材料,其物性数据源于中国科学院金属所,而1Cr11Ni2W2MoV源于材料手册[22]。
|
|
表 3 材料热导率 Table 3 Thermal conductivity of material |
|
|
表 4 材料屈服强度 Table 4 Yield strength of material |
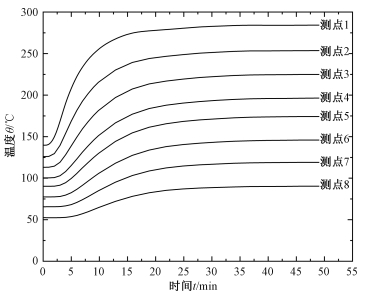
图 4为升高加热温度,两试件温度随时间基本变化关系。为避开瞬态变化段,获得稳态温度数据,在测温前,会将系统保温20~30 min,当10 min内各测点温度变化不超过0.2 ℃,即可记录温度数据和界面压力大小。
|
Download:
|
| 图 4 升高加热温度,两试件温度随时间基本变化关系 Fig. 4 Temperature of two specimens basically changing with time when increasing the heating temperature | |
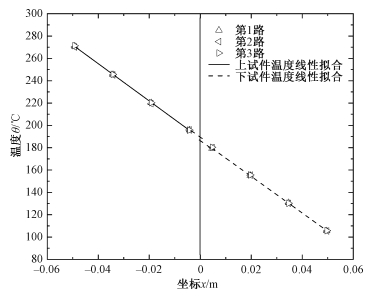
为校核实验系统准确性,对基本实验结果进行分析。表 5为某工况下不同测点3路温度数据对比结果,由表可知3路温度数据差异较小,最大偏差仅0.5 ℃。从图 5可知,两试件温度分布线性度非常好,针对后文每个工况,上下试件3路斜率相对变化量均小于2.5%,由此引起的接触热阻误差小于5%。以上基本实验结果说明测温设备精度高,实验系统保温性能好,通过该实验系统测得的接触热阻值很准确。
|
|
表 5 某工况不同测点3路温度对比 Table 5 Comparison of three-road temperatures at different measuring points for some working condition |
|
Download:
|
| 图 5 试件1和2温度分布基本情况 Fig. 5 The basic situation of temperature distribution on test specimen 1 and 2 | |
图 6为不同界面平均温度下,DD5和1Cr11Ni2W2MoV接触热阻随界面压力变化关系。两材料接触热阻随压力增大均逐渐减小。就DD5而言,当界面温度和压力分别位于155~292 ℃和47~203 MPa区间,其接触热阻在(2.17~7.74)×10-5 m2·K·W-1范围内变化。最小接触热阻值对应最高界面温度和压力工况,最大值则相反;而1Cr11Ni2W2MoV接触热阻变化范围为(0.85~3.15)×10-5 m2·K·W-1,分别在268 ℃和198 MPa与181 ℃和44 MPa取得。

|
Download:
|
| 图 6 不同界面平均温度下界面压力对两材料接触热阻的影响 Fig. 6 Effect of interface pressure on thermal contact resistance for two materials at different mean interface temperatures | |
这里以DD5材料为例进行分析,从图 6(a)可知,在界面温度155 ℃时,当压力从47 MPa加到203 MPa,DD5接触热阻从7.74×10-5 m2·K·W-1逐渐减小到5.08×10-5 m2·K·W-1,降低34%,且随着压力增加其减小幅度变慢,共下降94%。这是因为随着压力增大,接触凸起变形程度的加大和新增加的接触凸起使实际接触面积加大,从而减弱对流过界面热流的阻碍,界面热阻逐渐减小。其减小幅度逐渐变慢原因在于:实际接触面积与界面压力存在比例关系,随着压力增加,界面实际接触面积逐渐加大,但其相对增加量反而逐渐减小。相应地,界面接触热阻相对减小量逐渐减小,故随界面压力增加,其绝对减小量必定逐渐降低,即减小幅度变慢。
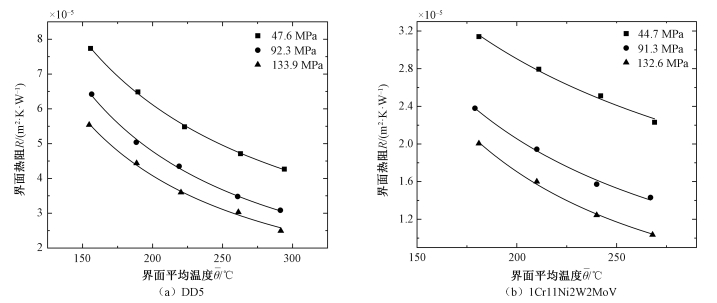
2.3 界面平均温度对接触热阻的影响图 7为不同界面压力下,DD5和1Cr11Ni2W2MoV材料接触热阻随界面平均温度变化关系。两材料接触热阻随界面温度升高均逐渐减小。由于研究的最高界面温度不到300 ℃,界面热辐射影响可忽略。与此同时,填充在接触间隙的空气热导率较小,比本文研究的固体材料热导率小3个数量级,再加上界面压力较大,接触面主要发生塑性变形,实际接触面积占名义接触面积比值基本位于1.5%~6.25%区间,而当界面压力小于10 MPa时,其比值小于1%。因此,相比间隙导热而言,相对较大的实际接触面积使得通过接触面的固体导热对界面热量传递起主导作用。所以,界面热阻主要来自于实际接触面导热产生的热阻。
|
Download:
|
| 图 7 不同界面压力下界面平均温度对两材料接触热阻的影响 Fig. 7 Effect of mean interface temperature on thermal contact resistance for two materials at different interface pressures | |
由实际接触面导热产生的热阻不仅与接触面积有关,还与固体热导率相关。热导率越大,接触面导热能力越强,热阻相应越小。但如图 7所示,对于DD5和1Cr11Ni2W2MoV,在界面压力约为45 MPa时,其接触热阻随温度的升高分别从7.74×10-5 m2·K·W-1降到4.27×10-5 m2·K·W-1和从3.15×10-5 m2·K·W-1降到2.23×10-5 m2·K·W-1,各自减小45%和29%,然而其热导率仅增加18%和6%。这是因为界面热阻还受材料力学参数硬度和屈服强度影响。该参数反映材料抵抗变形的能力,随着温度升高,材料硬度和屈服强度逐渐减小,在界面压力不变时,这会使得接触凸起变形程度增加,实际接触面积相应增大,从而引起接触热阻的减小。因此,界面平均温度对接触热阻的影响机制应归于其对材料热导率、硬度和屈服强度的共同影响。
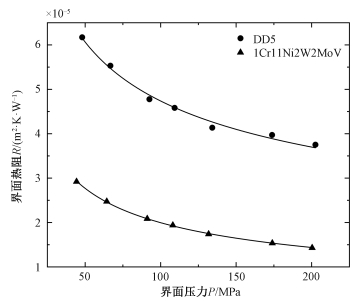
2.4 两种材料接触热阻比较图 8为界面平均温度θ=200 ℃时,DD5和1Cr11Ni2W2MoV材料接触热阻随界面压力变化关系。从2.3节温度对界面热阻的影响机理分析可知,材料间热导率、硬度或屈服强度差异性决定接触热阻不同。对于1Cr11Ni2W2MoV,在同一界面压力下,其接触热阻比DD5的更小。当界面压力为45 MPa时,1Cr11Ni2W2MoV的接触热阻与DD5的比值为1∶2.1,后者热导率与前者之比为1∶2.3,然而两者硬度相差不到1%,这说明两材料接触热阻差异主要来自热导率不同。与此同时,随着压力加大,两者差异逐渐缩小。当压力从45 MPa升至200 MPa时,差距从3.25×10-5 m2·K·W-1减至2.32×10-5 m2·K·W-1,缩小29%。这是因为当压力相对增加量相同时,两材料实际接触面积相对增加量保持一致。相应地,其接触热阻相对减小量一样。因此,在某一压力下,接触热阻小的材料,其界面热阻随压力增加,减小幅度小,接触热阻大的减小幅度自然大。正是由于减小速率不同,两材料接触热阻差异才随压力增大而逐渐缩小。
|
Download:
|
| 图 8 θ=200 ℃时不同压力下两材料接触热阻比较 Fig. 8 Comparison of thermal contact resistance for two materials under different interface pressures at θ=200 ℃ | |
上述两种材料接触热阻与界面压力和温度之间均存在幂律关系,拟合函数相关性基本在99.1%以上。接触热阻与界面压力的幂律关系已由Mikic[9]通过理论分析得到,而接触热阻与界面温度存在幂律关系主要原因是:温度通过改变材料热导率、硬度和屈服强度间接影响接触热阻,在本文相对较窄温度区间,上述物性与温度幂律关系较好。为更好地预测不同界面压力(45~200 MPa)和温度(150~300 ℃)下的接触热阻,DD5和1Cr11Ni2W2MoV实验数据已分别拟合为
| $R=1.829 \times 10^{-4}\left(\frac{\bar{\theta}}{\theta_0}\right)^{-1.132}\left(\frac{P}{H_0}\right)^{-0.355}, $ | (2) |
| $R=5.310 \times 10^{-5}\left(\frac{\bar{\theta}}{\theta_0}\right)^{-1.220}\left(\frac{P}{H_0}\right)^{-0.522}.$ | (3) |
式中H0/MPa是θ0=20 ℃时两接触材料较软者的维氏硬度。拟合公式可决系数分别为R2=0.979和0.968。式(2)和式(3)能较好地预测实验结果,尽管与实验数据最大误差各自是12.5%和18.5%,然而与91.4%和92.9%的实验数据相对误差分别要小于10%和12%。
3 结论本文基于发动机连接部件界面实际工况,根据稳态热流法自主设计搭建实验装置,测量不同温度(150~300 ℃)和压力(45~200 MPa)下DD5和1Cr11Ni2W2MoV材料接触热阻,并根据实验结果拟合得到接触热阻与界面压力和温度的关系式。结果表明:
1) 界面接触热阻主要来自实际接触面导热产生的热阻。随着界面压力和温度增加,接触热阻逐渐减小。温度对接触热阻的影响机制应归于其对材料热导率、硬度和屈服强度的共同影响。对于DD5和1Cr11Ni2W2MoV,其接触热阻变化范围分别为(2.17~7.74)×10-5 m2·K·W-1和(0.85~3.15)×10-5 m2·K·W-1。
2) 虽然接触热阻受材料硬度和屈服强度影响,但在相同界面压力和温度下,1Cr11Ni2W2MoV接触热阻比DD5小的主要原因是前者热导率比后者大。但由于减小速率不同,两者差异性随压力增大而逐渐缩小。当压力从45 MPa增加到200 MPa时,两者差距缩小29%。
3) 在本文研究工况范围内,接触热阻与界面压力和温度均存在幂律关系,DD5和1Cr11Ni2W2MoV的拟合关系式分别为:R=1.829×10-4(θ/θ0)-1.132(P/H0)-0.355和R=5.310×10-5(θ/θ0)-1.220(P/H0)-0.522。拟合公式能较好地预测实验结果,与92.9%的实验数据相对误差小于12%。
该研究为发动机部件优化设计、叶顶间隙控制和材料热防护提供基础数据,对航空发动机的研制具有参考价值。
| [1] |
刘松龄, 陶智. 燃气涡轮发动机的传热和空气系统[M]. 上海: 上海交通大学出版社, 2018.
|
| [2] |
姜浩峰. 哪些核心技术, 还在"卡脖子"?[J]. 新民周刊, 2018(26): 52-55. |
| [3] |
王祥和. 航空发动机热变形转子振动特性研究[D]. 哈尔滨: 哈尔滨工业大学, 2017.
|
| [4] |
牛冬生. 涡轮叶尖间隙数值分析和冷热态尺寸换算方法研究[D]. 南京: 南京航空航天大学, 2004.
|
| [5] |
姜远刚. 间隙主动控制系统中冷却流路的流动/换热特性研究[D]. 南京: 南京航空航天大学, 2013.
|
| [6] |
Chen Z. Surface integrity of broached Inconel 718 and influence of thermal exposure[D]. Linköping: Linköping University Electronic Press, 2014. DOI: 10.3384/lic.diva-111062.
|
| [7] |
Greenwood J A, Williamson J B P. Contact of nominally flat surfaces[J]. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences,, 1966, 295(1442): 300-319. Doi:10.1098/rspa.1966.0242 |
| [8] |
Cooper M G, Mikic B B, Yovanovich M M. Thermal contact conductance[J]. International Journal of Heat and Mass Transfer, 1969, 12(3): 279-300. Doi:10.1016/0017-9310(69)90011-8 |
| [9] |
Miki Ac'1 B B. Thermal contact conductance; theoretical considerations[J]. International Journal of Heat and Mass Transfer, 1974, 17(2): 205-214. Doi:10.1016/0017-9310(74)90082-9 |
| [10] |
Cui T F, Li Q, Xuan Y M, et al. Multiscale simulation of thermal contact resistance in electronic packaging[J]. International Journal of Thermal Sciences, 2014, 83: 16-24. Doi:10.1016/j.ijthermalsci.2014.04.006 |
| [11] |
Verma N N, Mazumder S. Extraction of thermal contact conductance of metal-metal contacts from scale-resolved direct numerical simulation[J]. International Journal of Heat and Mass Transfer, 2016, 94: 164-173. Doi:10.1016/j.ijheatmasstransfer.2015.11.026 |
| [12] |
Dai Y J, Gou J J, Ren X J, et al. A test-validated prediction model of thermal contact resistance for Ti-6Al-4V alloy[J]. Applied Energy, 2018, 228: 1601-1617. Doi:10.1016/j.apenergy.2018.06.134 |
| [13] |
Asif M, Tariq A. Correlations of thermal contact conductance for nominally flat metallic contact in vacuum[J]. Experimental Heat Transfer, 2016, 29(4): 456-484. Doi:10.1080/08916152.2015.1024352 |
| [14] |
Pan X S, Cui X Y, Liu S S, et al. Research progress of thermal contact resistance[J]. Journal of Low Temperature Physics, 2020, 201(3/4): 213-253. Doi:10.1007/s10909-020-02497-0 |
| [15] |
Wahid S M S, Madhusudana C V, Leonardi E. Solid spot conductance at low contact pressure[J]. Experimental Thermal and Fluid Science, 2004, 28(6): 489-494. Doi:10.1016/j.expthermflusci.2003.07.007 |
| [16] |
姬亚萌, 张卫正, 原彦鹏, 等. 复合隔热结构活塞界面材料接触热阻实验研究[J]. 工程热物理学报, 2020, 41(7): 1728-1734. |
| [17] |
Liu Y W, Ji Y M, Ye F H, et al. Effects of contact pressure and interface temperature on thermal contact resistance between 2Cr12NiMoWV/BH137 and γ-TiAl/2Cr12NiMoWV interfaces[J]. Thermal Science, 2020, 24(1 Part A): 313-324. Doi:10.2298/tsci191018470l |
| [18] |
Tang Q Y, He J J, Zhang W F. Influencing factors of thermal contact conductance between TC4/30CrMnSi interfaces[J]. International Journal of Heat and Mass Transfer, 2015, 86: 694-698. Doi:10.1016/j.ijheatmasstransfer.2015.03.035 |
| [19] |
Zheng X P, Liu D H, Wei D, et al. Experimental investigation of high temperature thermal contact resistance with interface material[J]. Theoretical and Applied Mechanics Letters, 2011, 1(5): 051009. Doi:10.1063/2.1105109 |
| [20] |
Xing L, Zhang L W, Zhang X Z, et al. Experimental investigation of contact heat transfer at high temperature based on steady-state heat flux method[J]. Experimental Heat Transfer, 2010, 23(2): 107-116. Doi:10.1080/08916150903402773 |
| [21] |
Dou R F, Ge T R, Liu X L, et al. Effects of contact pressure, interface temperature, and surface roughness on thermal contact conductance between stainless steel surfaces under atmosphere condition[J]. International Journal of Heat and Mass Transfer, 2016, 94: 156-163. Doi:10.1016/j.ijheatmasstransfer.2015.11.069 |
| [22] |
《中国航空材料手册》编辑委员会. 中国航空材料手册.第1卷.结构钢不锈钢[M]. 北京: 中国标准出版社, 2002: 658-676.
|
 2023, Vol. 40
2023, Vol. 40 


