引力位从地球内部到地球外部无处不在。当大地震发生时,地球内部物质产生位移,引起引力位扰动。因此,在地球自由振荡以及低频大尺度(如全球尺度)地震波场数值模拟中,引力位计算是一个不可避免的问题。但无论引力位还是引力位扰动,在地球内部均满足泊松方程,在地球外满足拉普拉斯方程,其边界条件均为在无穷远处衰减为零[1],这迫使我们需要利用数值方法求解一个无界微分方程。长期以来,为了避免求解该无界微分方程而采用Cowling近似[2],舍弃掉引力位扰动项。这会造成模拟波形的不准确,从而导致精细频谱分析困难,特别是对于地球自由振荡[3]、固体潮汐[4]等问题。
针对此类问题,常规的处理方法是将求解域设定在有限的范围内。例如将地球内部网格向外延伸到足够远的地球外(如数倍地球半径处),然后在这一人为指定的边界处设置边界条件,只要延伸得足够远,则对地球内部及近地表的引力位影响较小。该边界条件的选取有多种方法:例如Cai和Wang[5]提出的r-4近似假设,用于近似表示位置r处的函数值;Chaljub和Valette[6]采用球谐函数展开构建DtN算子,用于该边界条件的处理;Xu和Huo[7]使用Legendre多项式近似表示边界处的值。这些处理总体上都是通过对边界条件取值的近似来满足所需的计算精度。事实上,对于无界泊松问题,数学上很早就有研究[8],只是一些方法没有在地学中得到使用。
本文在延拓网格的基础上,运用无限元映射[9]的思想,直接通过构造插值多项式,自然地满足无穷远趋于零的边界条件,从而避免了对边界条件取值的近似处理,因而结果更准确。
本文采用谱元法[10]作为数值求解方法。谱元法是一种综合型方法,既保留了传统有限元方法处理复杂网格和边界的便利性,又确保了类似谱配置方法的高精度。考虑到全球尺度模拟的计算量和模型的复杂度(如S40RTS[11]地幔模型),本文采用2.5维[12-13]的控制方程。在2.5维假设下,引力位的计算简化到二维D形区域。由于对称轴的原因,轴单元的数值积分需要进行改进。本文采用Gerritsma和Phillips[14]提出的归一化方法,在轴单元引入GRL(Gauss-Radau-Legendre)数值积分。
为分析此模拟方法的有效性,本文开展了数值试验,以三维球对称实心球为例,数值模拟其引力位,并与解析解做对比。
1 方法 1.1 控制方程对于引力位Ψ以及引力位扰动ϕ,均满足泊松-拉普拉斯方程[1]:
| $\nabla^2 \mathit{\Psi}= \begin{cases}4 {\rm{ \mathsf{ π} }} g \rho, & \text { in V }, \\ 0, & \text { outside V }.\end{cases}$ | (1) |
| $\nabla^2 \phi(d)= \begin{cases}-4 {\rm{ \mathsf{ π} }} g \nabla \cdot(\rho d), & \text { in V, } \\ 0, & \text { outside V }.\end{cases}$ | (2) |
其中: g为地球的引力常数,取(6.673 84±0.000 12)×10-11 m3·kg-1·s-2;ρ为地球密度;d为地震引起的位移变化;V为整个地球。
为简化问题,方程(1)、(2)可以简写为
| $-\nabla^2 u(\boldsymbol{x})=s(\boldsymbol{x}) .$ | (3) |
其中s代表源项,是位置x的函数,在地球外部取0,在地球内部与密度有关。方程(3)对应的边界条件为
| $\lim\limits_{\boldsymbol{x} \rightarrow \infty} s(\boldsymbol{x})=0 .$ | (4) |
采用有限元方法,对方程(3)做弱形式有
| $\int_{\mathit{\Omega}} \nabla u \cdot \nabla \psi \mathrm{d} V=\int_{\mathit{\Omega}} s \cdot \psi \mathrm{d} V.$ | (5) |
其中ψ为测试函数。
1.2 离散与网格剖分在柱坐标系(r, θ, z)下,对3维方程(5)进行简化(2.5维)。考虑对称性,关于θ的运算可以忽略,此时位置x(r, θ, z)变为x(r, z)。相应地,体积元dV=rdrdθdz变成
| $\mathrm{d} \mathit{\Omega}=r \mathrm{~d} r \mathrm{~d} z.$ | (6) |
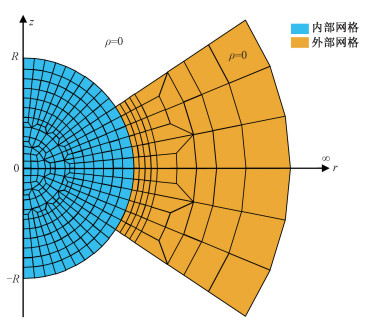
按照谱元法的要求,对求解域Ω进行四边形网格剖分,如图 1蓝色部分所示。本文采用doubling算法,在介质间断面处做加密处理。对于地球外部的网格延拓方案:首先,以地球网格为基础,对近地表处的网格进行局部加密;然后沿r向无穷远方向进行逐层延拓(如图 1黄色部分所示),每延拓一层,相应的延拓网格尺寸按指数增加,以保证延拓网格的稀疏性。
|
Download:
|
| 图 1 求解域四边形网格剖分示意图 Fig. 1 Schematic diagram of the quadrilateral meshing of the solution domain | |
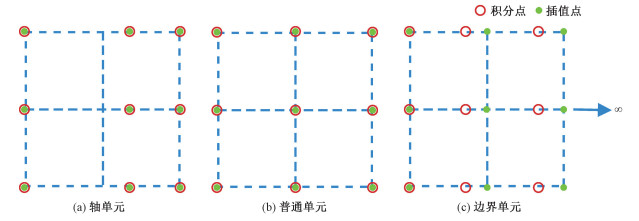
注意,这里面的网格单元有2种比较特殊(如图 2所示):第1种是轴单元,其所在的边有一个落在旋转轴上;第2种是边界单元,其所在的边有一个处于延拓的最外部。这2种单元的处理均与其他普通单元不同,普通单元的插值和积分均采用GLL(Gauss-Lobatto-Legendre)点。轴单元由于旋转轴使得r→0,这在数值积分时会引入异常,因此在涉及轴单元的位置,归一化r带来的权重函数恰好方便采用GLJ(Gauss-Lobatto-Jacobi)积分,详细见后文。边界单元为了应用无限元映射法,致使将无穷远作为插值节点,因此对应地选择GRL积分[15],避免选择无穷远作为计算自由度。
|
Download:
|
| 图 2 单元类型以及对应的插值和积分节点选择 Fig. 2 Cell type and corresponding interpolation and integration node selection | |
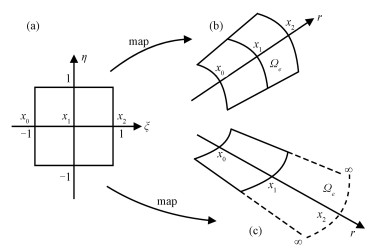
对于每一个四边形单元,通过等参元映射的办法可以将原四边形单元映射到一个[-1, 1]×[-1, 1]的标准正方形上(如图 3(a)所示),其中位置x=(r, z)可以用等参元ξ=(ξ, η)表示,其中ξ, η∈[-1, 1]。
|
Download:
|
| 图 3 等参元映射示意图 Fig. 3 Schematic diagram of isometric mappings | |
这样,对于每一个单元Ωe所示可以通过等参元定义形函数
| $x(\boldsymbol{\xi})=\sum\limits_{\alpha=1}^{n_\alpha} \boldsymbol{x}_\alpha N_\alpha(\boldsymbol{\xi}) .$ | (7) |
对于普通单元(如图 3(b)所示),(ξα, ηβ)α, β=0, …, N取GLL点,这样插值形函数Nα(ξ)可以采用Lagrange插值多项式。
而对于边界单元,其外边界并没有达到无穷远处。无限元映射法[9]可以很好地解决该问题(如图 3(c)所示),其形函数定义为
| $x=N_0 x_0+N_1 x_1=\left(1+\frac{2 \xi}{1-\xi}\right) x_0-\frac{2 \xi}{1-\xi} x_1 .$ | (8) |
其中等参元与位置的对应关系如下
| $\begin{array}{ll} \xi=-1, & x=x_0 ; \\ \xi=0, & x=x_1 ; \\ \xi=1, & x=x_2=\infty . \end{array}$ | (9) |
这样,无限元映射就将无穷远点映射到了等参元中的右端点。换言之,在等参元坐标系下,无穷远点变成了正常的插值点,因此可以直接使用零边界条件,然后套用谱元法求解。
1.4 插值与积分对于任意函数f(x)可以用Lagrange插值多项式进行拟合
| $f(x(\xi, \eta)) \approx \sum\limits_{\alpha=0}^N \sum\limits_{\beta=0}^N f\left(\xi_\alpha, \eta_\beta\right) \ell_\alpha(\xi) \ell_\beta(\eta).$ | (10) |
其偏导数可以写为
| $\left\{\begin{array}{l} \frac{\partial f}{\partial \xi}(x(\xi, \eta))=\sum\limits_{\alpha, \beta=0}^N f^{\alpha \beta} \ell^{\prime}{ }_\alpha(\xi) \ell_\beta(\eta), \\ \frac{\partial f}{\partial \eta}(x(\xi, \eta))=\sum\limits_{\alpha, \beta=0}^N f^{\alpha \beta} \ell_\alpha(\xi) \ell^{\prime}{ }_\beta(\eta) . \end{array}\right.$ | (11) |
对应插值公式(10),任意函数f(x)的积分可以写为如下形式
| $\int_{\mathit{\Omega}_e} f(x(\xi, \eta)) \mathrm{d} \xi \mathrm{d} \eta \approx \sum\limits_{i, j=0}^N \omega_i \omega_j f^{i j} .$ | (12) |
其中ωi, ωj为对应的积分权重。
不同正交多项式对应的插值节点和积分权重不同。表 1给出了本文用到的3种方法对应的插值节点和积分权重的值(多项式取2阶)。
|
|
表 1 正交多项式插值点与积分权重对比(2阶) Table 1 The comparison of interpolation points and integral weights for different orthogonal polynomials (2nd order) |
单元刚度矩阵可以写成
| $\boldsymbol{K}_e=\int_{\mathit{\Omega}_e} \nabla \psi \cdot \nabla u r \mathrm{~d} r \mathrm{~d} z=\int_{\mathit{\Omega}_e} \nabla \psi \cdot \nabla u\left|\mathcal{J}_e\right| r \mathrm{~d} \xi \mathrm{d} {\eta} .$ | (13) |
类似地可以得到对应的单元载荷向量Fe
| $\boldsymbol{F}_e=\int_{\mathit{\Omega}_e} s \cdot \psi r \mathrm{~d} r \mathrm{~d} z=\int_{\mathit{\Omega}_e} s \cdot \psi\left|\mathcal{J}_e\right| r \mathrm{~d} \xi \mathrm{d} \eta .$ | (14) |
其中
| $\mathcal{J}_e=\left\|\begin{array}{ll} \frac{\mathrm{d} r}{\mathrm{~d} \xi} & \frac{\mathrm{d} z}{\mathrm{~d} \xi} \\ \frac{\mathrm{d} r}{\mathrm{~d} \eta} & \frac{\mathrm{d} z}{\mathrm{~d} \eta} \end{array}\right\|.$ | (15) |
由于体积元(6)中存在因子r,使得应用传统的GLL积分在左端点为零,从而缺少了对左端点物理量的约束。为了解决该问题,Gerritsma和Phillips[14]引入了归一化半径的方法。例如,使用权函数ω(ξ)=1+ξ对r进行归一化处理,方程(13)可以写为
| $\boldsymbol{K}_e=\int_{\mathit{\Omega}_e} \nabla u \cdot \nabla \psi \frac{r}{\omega} \omega \mathrm{d} r \mathrm{~d} z .$ | (16) |
当ξ→-1时,η→0和ω→0,由此利用洛必达(L’Hôpital’s)法则有
| $\lim\limits_{\xi \rightarrow-1} \frac{r}{\omega}=\lim\limits_{\xi \rightarrow-1} \frac{r(\xi, \eta)}{1+\xi}=\left.\frac{\partial r}{\partial \xi}\right|_{\xi=-1} .$ | (17) |
由此可以定义归一化半径
| $\tilde{r}= \begin{cases}\frac{r}{\omega}, & \text { if } r>0, \\ \frac{\partial r}{\partial \xi}, & \text { if } r=0 .\end{cases}$ | (18) |
而剩下的ω恰好为GLJ积分的权函数。
1.7 组刚与求解经过上述步骤后,每一个单元都可以得到一个单元刚度矩阵Ke和对应的单元载荷向量Fe。按照自由度将单元刚度矩阵Ke和单元载荷向量Fe组合起来,得到总体刚度矩阵K和总体载荷向量F。根据方程(5),K与F满足方程
| $\boldsymbol{K} \boldsymbol{U}=\boldsymbol{F}.$ | (19) |
其中U对应要求的自由度。由于K的稀疏性,式(19)可以使用共轭梯度(conjugate gradient,CG)算法有效求解。
2 数值试验本文以均匀实心球(半径为R=500 km)为例(具体参数的物理意义可以参看图 1),计算其引力位Ψ,Ψ满足方程(1)。当r<R时,ρ取常数ρ0=1.0 kg/m3;当r>R时,ρ=0。
上述问题的解析解[16]为:
| $\mathit{\Psi}= \begin{cases}2 {\rm{ \mathsf{ π} }} g \rho\left(R^2-\frac{1}{3} r^2\right), & r \leqslant R, \\ \frac{4}{3} \frac{{\rm{ \mathsf{ π} }} \rho g R^3}{r}, & r>R .\end{cases}$ | (20) |
考虑到该问题满足轴对称性条件,可以采用上文描述的网格剖分方法(如图 1所示)。整个实心球对应的半圆(D形区,如图 1蓝色部分所示)域剖分为1 630个四边形单元。针对实心球外的真空区域,网格分别按照2、5、7、10层的层数对外部网格进行延拓(如图 1黄色部分所示),最远延拓到约8.6倍实心球半径处。除去最开始延拓需要对近地表网格加密,后面每向外延拓一层,网格增加60个单元,增加量不足原问题的4%。
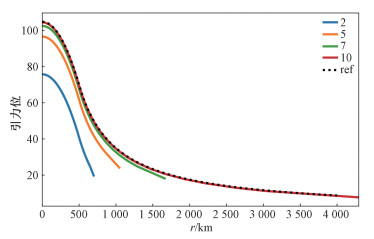
运用上文的无限元-谱元混合法进行数值模拟,结果如图 4所示:当求解域贴近实心球表面时(蓝色实线),模拟结果并不能很好地收敛于解析解(黑色虚线)。随着外部稀疏网格层数(从2层增加到10层)的增加,数值模拟结果逐步收敛于解析解。当延拓网格达到7层(绿色实线)约3.3倍实心球半径时,基本能满足模拟的计算需求,进一步达到10层(红色实线) 约8.6倍实心球半径时,模拟结果与解析解吻合。
|
Download:
|
| 图 4 数值试验模拟结果对比 Fig. 4 Comparison of numerical test simulation results | |
通过数值试验,验证了本文提出的无限元-谱元混合法在引力位计算模拟中的真实准确性。只需要有限的几层网格延拓,并不需要真的把求解域延伸到无穷远,即可实现对无穷远边界条件的把控。同时引入的2.5维近似假设可以很好地解决3维真实地球模型计算的复杂度。对于传统的PREM模型[12]可以直接应用此方法。对于更复杂的地球模型(如S40RTS[11]),可以考虑保留其有效的球谐展开阶次,利用傅里叶变换转化为本文的2.5维问题[13]。最后,本文通过无限元-谱元混合法的引入,弥补了传统引力位边界条件近似处理的缺陷,为地球自由振荡和低频大尺度(如全球尺度)地震波场数值模拟提供有效支持。
| [1] |
Woodhouse J H, Deuss A. Theory and observations-earth's free oscillations [M]//Treatise on Geophysics. Amsterdam: Elsevier, 2015: 79-115 DOI: 10.1016/b978-0-444-53802-4.00002-6.
|
| [2] |
Cowling T G. The non-radial oscillations of polytropic stars[J]. Monthly Notices of the Royal Astronomical Society, 1941, 101(8): 367-375. Doi:10.1093/mnras/101.8.367 |
| [3] |
Yan R, Woith H, Wang R J, et al. Earth's free oscillations excited by the 2011 Tohoku Mw 9.0 earthquake detected with a groundwater level array in mainland China[J]. Geophysical Journal International, 2016, 206(3): 1457-1466. Doi:10.1093/gji/ggw213 |
| [4] |
Dahlen F A, Tromp J. Theoretical global seismology[M]. Princeton: Princeton University Press, 2021. Doi:10.1515/9780691216157
|
| [5] |
Cai Y E, Wang C Y. Fast finite-element calculation of gravity anomaly in complex geological regions[J]. Geophysical Journal International, 2005, 162(3): 696-708. Doi:10.1111/j.1365-246X.2005.02711.x |
| [6] |
Chaljub E, Valette B. Spectral element modelling of three-dimensional wave propagation in a self-gravitating Earth with an arbitrarily stratified outer core[J]. Geophysical Journal International, 2004, 158(1): 131-141. Doi:10.1111/j.1365-246X.2004.02267.x |
| [7] |
Xu C Y, Huo Z J. Numerical simulation of gravity anomaly based on the unstructured element grid and finite element method[J]. Mathematical Problems in Engineering, 2020, 2020: 3604084. Doi:10.1155/2020/3604084 |
| [8] |
Hejlesen M M, Rasmussen J T, Chatelain P, et al. A high order solver for the unbounded Poisson equation[J]. Journal of Computational Physics, 2013, 252: 458-467. Doi:10.1016/j.jcp.2013.05.050 |
| [9] |
O.C Z, R.L T, Zhu J Z. The finite element method: Its basis and fundamentals[M]. Sixth. Burlington (Mass.): Elsevier, 2005.
|
| [10] |
Chaljub E, Komatitsch D, Vilotte J P, et al. Spectral-element analysis in seismology[J]. Advances in Geophysics. Elsevier, 2007, 48: 365-419. Doi:10.1016/S0065-2687(06)48007-9 |
| [11] |
Ritsema J, Deuss A, van Heijst H J, et al. S40RTS: a degree-40 shear-velocity model for the mantle from new Rayleigh wave dispersion, teleseismic traveltime and normal-mode splitting function measurements[J]. Geophysical Journal International, 2011, 184(3): 1223-1236. Doi:10.1111/j.1365-246X.2010.04884.x |
| [12] |
Nissen-Meyer T, Fournier A, Dahlen F A. A two-dimensional spectral-element method for computing spherical-earth seismograms-Ⅰ. Moment-tensor source[J]. Geophysical Journal International, 2007, 168(3): 1067-1092. Doi:10.1111/j.1365-246X.2006.03121.x |
| [13] |
Nissen-Meyer T, Fournier A, Dahlen F A. A 2-D spectral-element method for computing spherical-earth seismograms-Ⅱ. Waves in solid-fluid media[J]. Geophysical Journal International, 2008, 174(3): 873-888. Doi:10.1111/j.1365-246X.2008.03813.x |
| [14] |
Gerritsma M I, Phillips T N. Spectral element methods for axisymmetric stokes problems[J]. Journal of Computational Physics, 2000, 164(1): 81-103. Doi:10.1006/jcph.2000.6574 |
| [15] |
Shen J, Tang T. Spectral and high-order methods with applications[M]. Beijing: Science Press, 2006.
|
| [16] |
李瑞浩. 重力学引论[M]. 北京: 地震出版社, 1988.
|
 2024, Vol. 41
2024, Vol. 41 


