卫星帆板作为卫星整个生命周期的能源提供部件，在卫星的健康状态评估中占有非常重要的比重。根据对2003—2021年91颗卫星在轨典型故障案例的分析，供电分系统出现故障的比率在所有分系统中排名最高，占比44%，其次是推进分系统和控制分系统，分别占比26%和16%^[1]。因此通过分析卫星帆板相关指数来判断卫星帆板当前的健康状态就显得至关重要。而卫星帆板温度遥测数据就是可以直接反映当前帆板工作状态的具体指标之一，该指标主要受到太阳、地球、卫星本体3方面的影响，具体包括太阳入射角、地球反照率、卫星本体温度等因素。卫星在发射升空进入轨道之后，就会按照预先设置的特定轨道严格恪守物理学定律进行周期性运动。即使考虑到轨道摄动、近地卫星受到大气层影响而降低高度、卫星执行任务时引起的姿态改变，也可以将其看作是渐周期性运动，这是本文采用自回归神经网络对卫星帆板温度遥测数据进行缺失值插补的根本原因。本文采用的卫星帆板温度遥测数据采样周期为256 s，遥测数据缺失情况主要是从连续缺失几个点到连续缺失1轨乃至2轨，为将缺失值尽可能多地插补出来，本文采用根据历史数据预测未来2轨的方法构建神经网络。

目前的时序缺失数据的插补方法已经比较完备，按照插补函数中残差存在与否主要包括确定性插补和随机性插补两个方法^[2]，其中确定性插补方法又包括最近邻插补^[3]、多项式插补^[4]、基于距离权重的插补^[5]、基于信号分析的插补如傅里叶分析等^[6]；随机性插补方法又包括回归插补方法^[4]、自回归插补方法^[7]、机器学习插补方法如ANN神经网络(artifical neural network, ANN) ^[8]、基于数据驱动的插补方法如K近邻^[9]、基于Kriging的插补方法等^{[2, 10]}。按照插补变量的维度又可以分为单变量插补方法和多变量插补方法，常见的单变量插补方法包括直接删除法、基于统计学的插补方法如均值插补、基于机器学习的插补方法等，其中基于机器学习的插补方法又包括回归插补^[4]、K近邻插补^[9]、极大似然插补、多重插补等，多变量插补方法包括主成分分析插补^[11]、基于概率矩阵分解的插补等^[12]。本文使用的模型是属于机器学习插补的范畴，涉及的卫星帆板温度遥测数据则是单变量，因此也属于单变量插补。传统的确定性插补方法在面对缺失数据较少以及主要缺失点分布在光滑缓变区域时较为有效，一旦数据点缺失比较多且主要分布在短期剧烈变化的区域，插补效果就会很差，而随机性插补方法面对这一问题就会表现出其优越性。Babu和Sure^[13]使用自回归移动平均模型(autovegressive integrated moving average model, ARIMA)和ANN的混合模型对诸如太阳黑子和用电价格的时间序列进行预测插补，进一步提高了模型的预测精度，取得了较好的效果。Hundman等^[14]使用长短时记忆网络(long short term memory network, LSTM)对卫星遥测数据建模预测，并提出自适应阈值算法以达到卫星异常数据检测的目的。王少影等^[15]使用随机森林(random forest, RF)、支持向量机(support vector machine, SVM)、人工神经网络ANN 3种机器学习模型对若尔盖高寒湿地生态系统研究站2016年感热、潜热以及净生态系统交换通量序列进行插补，取得了很棒的插补效果。Raubitzek和Neubauer^[16]提出一种分形插值方法以改进神经网络对困难时间序列数据的预测。

本文处理的遥测数据连续缺失较多，从连续缺失几个点到连续缺失1或2轨的情况都比较常见，且连续缺失点在光滑缓变区域以及短时剧烈变化区域均有分布，因此采用确定性插补方法效果不理想。目前在时序数据插补领域应用研究中，LSTM、ANN等神经网络是使用较为广泛的方法，但是却具有模型训练困难、模型训练时间长、梯度不稳定等缺点。为达到较好的缺失插补效果，本文采用加入了注意力机制的时间卷积网络(time convolution network with squeeze and excitation, SE-TCN)。目前时间卷积网络(time convolution network, TCN)^[17]已在音频合成^[18]、单词语言建模^[19]、机器翻译^[20]等领域取得优良效果，但其在多步预测任务中存在短期剧烈变化处模型特征表征能力不足的问题，因此采用squeeze-and-excitation networks^[21]中的通道注意力机制对TCN进行改进，以增强TCN网络的特征提取能力^[22]。

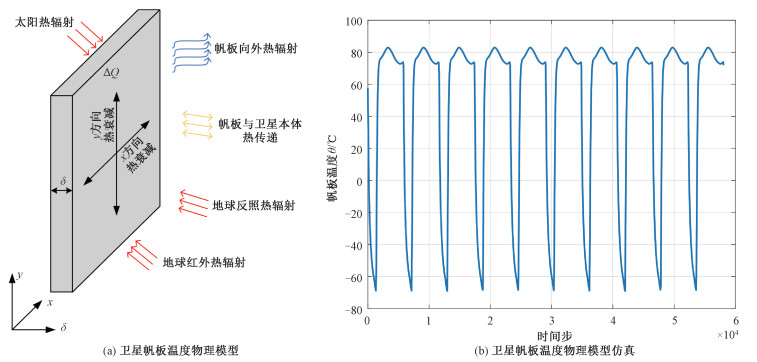
1 基本理论 1.1 帆板温度物理模型

根据真实的太空环境，能量守恒定律，以及有限差分理论，帆板温度物理模型的表达式如下所示^[23]

$ \begin{gathered} \delta \rho c \frac{\partial \theta(t)}{\partial t}+\omega=Q_1(t)-Q_2(t)+Q_3(t)+ \\ Q_4(t)+Q_5(t)+Q_i(t), \end{gathered} $

(1)

其中：Q₁(t)表示卫星帆板在x和y方向的热衰减对帆板各处温度的影响，Q₂(t)表示卫星帆板向外热辐射损失的热量，Q₃(t) 表示太阳对卫星帆板的热辐射带来的热量，Q₄(t)表示地球对帆板的反照热辐射带来的热量，Q₅(t)表示地球对帆板的红外热辐射带来的热量，Q_i(t)表示来自卫星本体的热量。它们的具体计算公式如下，公式中各个符号的物理含义详见表 1。

$ \left\{\begin{array}{l} Q_1(t)=\delta\left[\frac{\partial}{\partial x}\left(\lambda_x \frac{\partial \theta(t)}{\partial y}\right)+\right. \\ \ \ \ \left.\frac{\partial}{\partial y}\left(\lambda_y \frac{\partial \theta(t)}{\partial y}\right)\right], \\ Q_2(t)=\sigma \varepsilon\left(\theta^4(t)-\theta_{\mathrm{amb}}^4(t)\right), \\ Q_3(t)=\iint\limits_{\varOmega_{\mathrm{s}}} \frac{1}{\varphi_{\mathrm{s}}} \frac{\partial}{\partial y} \frac{\partial Q_{\mathrm{s}}(t)}{\partial x} \cos \left(\beta_{\mathrm{s}}(t)\right) \mathrm{d} x \mathrm{d} y, \\ Q_4(t)=\iint\limits_{\varOmega_{\mathrm{s}}} \frac{\rho_0}{\varphi_{\mathrm{s}} \alpha} \frac{\partial}{\partial y} \frac{\partial Q_{\mathrm{s}}(t)}{\partial x} X_1 \mathrm{d} x \mathrm{d} y, \\ Q_5(t)=\iint\limits_{\varOmega_{\mathrm{s}}} \frac{1-\rho_0}{4 \varphi_{\mathrm{s}} \alpha} \frac{\partial}{\partial y} \frac{\partial Q_{\mathrm{s}}(t)}{\partial x} X_2 \mathrm{d} x \mathrm{d} y . \end{array}\right. $

(2)

图 1(a)是卫星帆板的物理模型，对应式(1)和式(2)。设置初始值后，经过多次迭代，温度将趋于稳定，稳定状态是吸收和辐射之间的平衡。仿真结果如图 1(b)所示，从一段时间的仿真结果可以看出，在较短时间范围内，帆板温度数据具有很强的规律性和周期性，但是物理仿真对于缺失值的插补至少有两点不足。其一，从式(1)和式(2)来看，在计算过程中存在多次微分积分运算和参数调整，导致有限元网格优化计算成本高、难度大；其二，物理建模并未考虑到影响温度变化的所有因素，插值的准确度并不高，理论计算和实际的遥测数据会因为环境的不同而有所差异。考虑到物理模型插值的效果，采用物理建模的方法对帆板温度遥测数据进行填补并不可行。同时由于仿真数据在短时间范围内的渐周期性，采用针对时序数据的神经网络对缺失值进行插补具有可行性。

1.2 时间卷积网络模型

之前介绍了多种基于机器学习的时间序列插值方法，如ARIMA、ANN、SVM、LSTM、TCN、SE-TCN等等，考虑到本文处理的卫星帆板温度遥测数据的渐周期特性，使用SE-TCN^[22]可以解决ARIMA、ANN等模型的周期描述性不强带来的对历史数据的信息提取不足、LSTM等模型的训练周期长、TCN模型对时序数据剧烈变化区域特征提取能力弱等问题。

1.2.1 因果卷积

TCN网络基于两个基本准则^[17]: 其一，因果卷积网络输出的结果与输入具有相同的长度; 其二，网络没有从未来到过去的信息“泄露”，即$\hat{y}_t $仅依赖x₀, …, x_t计算获得，而不依赖于未来的输入x_t+1, …, x_T。

1.2.2 膨胀卷积

膨胀卷积是为解决简单因果卷积感受野能力有限，从而随着网络层数的增加，每层的感受野只能线性增加带来的网络复杂、层数高、难以训练等问题。TCN引入了膨胀卷积^[17]，可以使感受野大小成指数式增长。对于一维输入时间序列$x \in \mathbb{R}^n $以及滤波器f∶小成指数式增长。对于一维输人时间序列$ f:\{0, \cdots, k-1\} \rightarrow \mathbb{R}$，空洞卷积在t时刻的结果如下

$ F(t)=\left(\boldsymbol{x}_d^* f\right)(t)=\sum\limits_{i=0}^{k-1} f(i) \cdot x_{t-d \cdot i} . $

(3)

其中: d是膨胀因子，k是滤波器大小，t-d·i表示历史数据的方向，x_t-d·i表示输入序列x在时刻t之前的第d·i个分量。每个卷积层的感受野计算公式如下

$ \text { receptive field }=(k-1) d+1. $

(4)

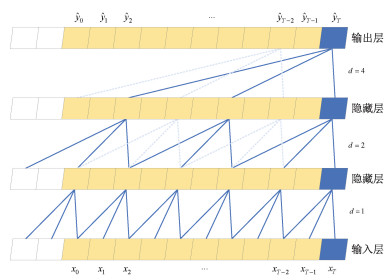
可以选择较大的滤波器大小k或者增加膨胀因子d来增加感受野。第i层的膨胀因子通常为O(2ⁱ)。关于膨胀因果卷积网络架构可见图 2。

1.2.3 残差连接

残差连接是训练深层网络的有效方法，它使得网络以跨层的方式传递信息，而且可以防止网络过深导致出现梯度消失的问题^[17]。残差块包含两层的卷积以及非线性映射，在每层中还使用权重正则化和Dropout层来正则化网络以防止深层网络的过拟合，此外还包含1×1卷积，其作用是降维，目的是为了两层相加时特征图数量相同。

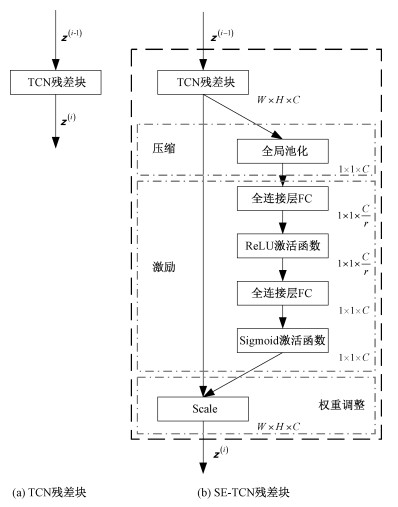
1.3 注意力机制

注意力机制是计算机视觉领域常用的模块，它的提出是为解决在卷积池化过程中特征图的不同通道所占的重要性不同而带来的损失问题^[21]。在传统的卷积池化过程中，默认特征图的每个通道是同等重要的。而在实际的问题中，不同通道的重要性是有差异的。注意力机制模块(squeeze-and-excitation, SE)包括3个部分: 压缩(squeeze)、激励(excitation)和权重调整(scale)。TCN残差模块和SE-TCN残差模块的对比结果如图 3所示。图中TCN残差块输出的特征图维度设为W×H×C，经过全局池化层的压缩操作之后，输出维度变为1×1×C，得到当前特征图的全局压缩特征量。接下来是激励操作，通过两层全连接的Bottleneck结构得到特征图中每个通道的权值，并将加权后的特征图作为下一层网络的输入。第1个全连接层含有C/r个神经元，输入维度为1×1×C，输出维度为1×1×C/r，其中r是一个缩放参数，这个参数的目的是为减少通道个数从而降低计算量。第2个全连接层含有C个神经元，输入维度为1×1×C/r，输出维度为1×1×C。最后是权重调整操作，将激励操作输出的特征图维度调整到和原特征图维度相同，即将维度从1×1×C调整到W×H×C。

2 遥测数据及模型结构 2.1 遥测数据

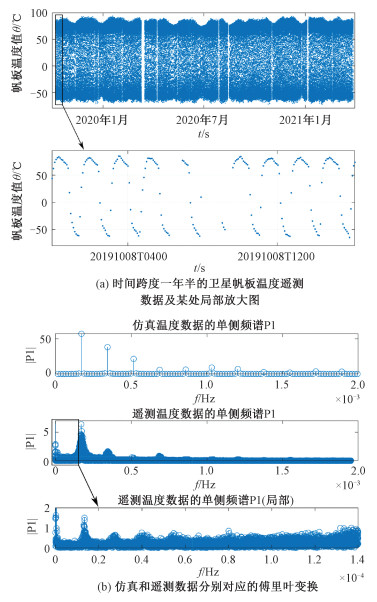
图 4展示了遥测及仿真数据的相关统计特性，其中图 4(a)是时间跨度一年半的卫星帆板遥测数据全览及某一段时间局部图，采样周期为256 s，卫星绕地球1圈即1轨会采样23~24个点，一天大概会产生15轨遥测数据。数据缺失具有以下几种情况：连续缺失1~2个采样点；连续缺失3个采样点至半轨；连续缺失半轨至1轨；连续缺失1~2轨。针对连续缺失1~2个采样点的情况，一般发生在数据较为平滑的区域，可以采用线性插值或者样条插值的办法进行初步填补，使得处理后的数据遥测尽可能少地出现间断点，为之后尽可能多地构建数据集样本做出贡献。至于连续缺失3个点至2轨的情况，不能简单使用统计学方法进行插值，因为连续缺失点较多，再使用样条插值等方法就会引入大量误差，使得插值后的曲线完全不符合历史数据走向，因此有必要引入时间卷积神经网络对缺失的数据进行插补。

2.2 模型结构

从直观上来分析，卫星围绕地球公转，而地球围绕太阳公转，公转可以理解为周期性运动，卫星帆板温度主要受到太阳、地球、卫星本体的影响。卫星在阳照区未执行任务的时候姿态稳定，为让帆板最大程度获取太阳能，帆板表面和太阳入射光是垂直关系，在执行任务的时间段才会有短暂的姿态改变，而在地影区卫星也是姿态稳定的，所以卫星姿态改变对温度变化造成的影响可以忽略。图 4(b)前2幅图分别是帆板温度仿真数据和帆板温度遥测数据对应的傅里叶变换，可以看到这2幅图都是由主要的几个峰和一些幅度较小的信号量组成，遥测数据傅里叶变换中频率为0附近的几个频点是由于遥测数据的缺失造成的，可以忽略。这从数据的频域上进一步反映了帆板温度数据属于和时间密不可分的时间序列。通过以上分析，可以认为帆板温度遥测数据是与时间密切相关的渐周期性时间序列，可以采用处理时间序列效果较好的时间卷积网络进行建模。

卷积神经网络建模本质是找到从一段历史时序数据到一段未来时序数据的映射函数，帆板温度数据相邻两轨的数据由于时间上连续，间隔时间较短，差异也比较小。如果直接使用前一轨作为模型输入，后一轨作为模型输出，从而建立映射模型，那么模型纳入考量的历史数据太少，即感受野太小，模型过于简单，模型对于训练集和测试集的拟合程度都不会好，造成欠拟合。为增加模型复杂度，在模型层与层之间的滤波器个数k和扩张因子d一定的情况下，可以通过增加输入维度，即增加输入层感受野来达到目的。而且，从图 4(b)中仿真数据和遥测数据的离散傅里叶变换来看，在误差允许范围内，排除幅度较低的高频信号，确定信号频域右边界，就可以将帆板温度数据看作众多正余弦信号的叠加。此外，图 4(b)中第3幅图可以看到，长周期低频信号量信息较为丰富，尽可能多地增加输入层维度，卷积神经网络也将尽可能多地纳入长周期的信号和多轨短周期的信号，使得神经网络针对不同频率段的历史信息都能进行学习。但是如果模型过于复杂，就会造成训练时间长、训练资源占用高、模型过拟合等情况。

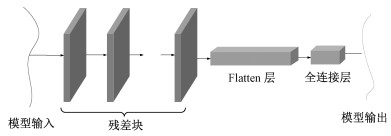
构建模型结构时需要考虑造成数据缺失的原因(主要包括组帧错误和入境时间短)带来的影响。组帧错误是随机发生的，造成的影响仅限于出现时间或者温度维度上的离群值，把离群值剔除即可，一般会带来零星采样点的缺失。入境时间短是造成数据缺失的主要原因，会造成遥测数据缺失几个零星的采样点到2轨不等，在极少情况下，会造成连续多轨的缺失。由于本文处理的帆板温度遥测数据的基本缺失场景是连续缺失最长不超过2轨数据，为尽量补齐缺失数据，设定模型输出维度为2轨。模型输入需要取模型输出序列之前的一段连续时间序列，而帆板温度遥测数据一天大约15轨数据中能连续的数据只有7轨左右。考虑到遥测数据缺失的特点、尽可能多地增加感受野、模型复杂度等因素的影响，取模型输入为连续5轨的数据。确定了模型输入输出维度之后，接着根据1.2节的计算公式初步确定所需残差块的最小数目，残差块数目越多，代表模型结构越复杂。为使得模型更好的拟合数据集，需要调节残差块数目以得到拟合最好的模型。模型在最后一个残差块后面加了Flatten层，把最后一个残差块输出的高维数据“碾压”成一维数据，而Flatten后面的全连接层在整个卷积神经网络中起到“分类器”的作用，再将上述一维数据映射成2轨的未来数据，本文中SE-TCN模型结构如图 5所示。

2.3 算法流程

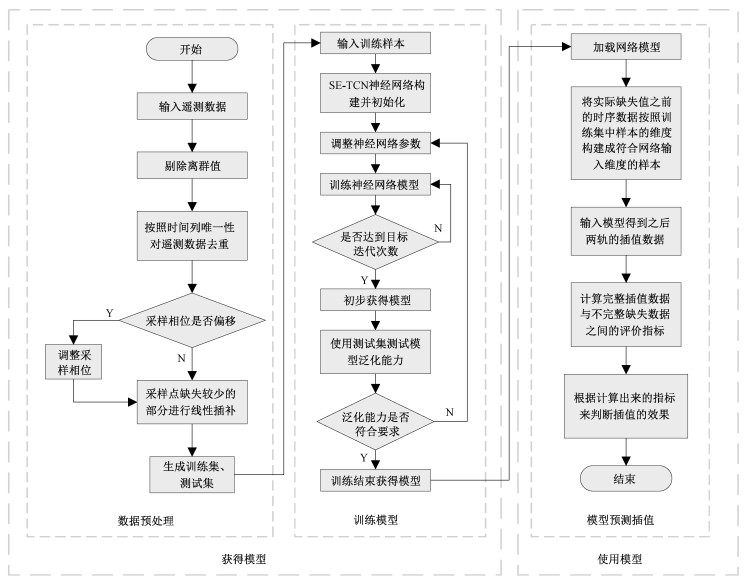
算法流程主要包括3个部分：数据预处理、模型的训练、使用训练好的模型进行预测插值。图 6是算法流程图。

1) 数据预处理

① 卫星帆板遥测数据时间上和温度值上离群值的去除、时间上的去重、采样相位的偏移矫正。

② 按照神经网络模型的输入输出维度，对上面处理好的数据进行数据集的构建。

2) 模型的训练

① 构建模型并初始化，加载训练集进行训练，训练次数达到目标迭代次数或者模型对训练集的拟合程度达到目标时，得到初步训练好的网络模型。

② 使用测试集对初步得到的模型进行泛化能力评估，即评价指标达到目标范围内，认为模型训练完成，否则回到第①步。

3) 使用训练好的模型进行预测插值

① 对于遥测数据中的缺失部分，根据模型的输入维度，读取缺失数据之前一定长度的历史数据，载入模型中将会输出一段完整的插值序列。

② 计算不完整的缺失数据和完整的插值数据之间的评价指标，以判断实际插值的效果。

3 实验结果 3.1 评价指标

为评价模型的性能，引入机器学习回归任务中常用的评价指标，分别是平均绝对误差(mean absolute error, MAE)、均方根误差(root mean square error, RMSE)和相关系数(related coefficient, R)^[24-25]。为计算测试集的评价指标，需要用到L₁、L₂范数的概念，

$ L_p(\boldsymbol{x})=\|\boldsymbol{x}\|_p=\left(\sum\limits_{i=1}^m\left|x_i\right|^p\right)^{\frac{1}{p}} . $

(5)

式(5)是向量x的L_p范数的定义，其中，x=(x₁, x₂, …, x_m), m表示向量x的维数。

MAE、RMSE、R 3种评价指标以及均方差(mean squared error, MSE)的计算方法分别由下式给出。其中，N表示测试集样本个数，M表示样本真实值和预测值的维数，$\boldsymbol{y} \in \mathbb{R}^{N \times M} $和$\hat{\boldsymbol{y}} \in \mathbb{R}^{N \times M} $分别表示测试集对应的真实值和预测值，$\boldsymbol{y}_i \in \mathbb{R}^M $和$ \hat{\boldsymbol{y}}_i \in \mathbb{R}^M$分别表示第i个样本的真实值和预测值，$\boldsymbol{y}_i=\left(y_{i 1}, y_{i 2}, \cdots, y_{i M}\right)^{\mathrm{T}} $, 以及$ \hat{\boldsymbol{y}}_i=\left(\hat{y}_{i 1}, \hat{y}_{i 2}, \cdots, \hat{y}_{i M}\right)^{\mathrm{T}}$。$ \operatorname{Cov}(\boldsymbol{y}, \hat{\boldsymbol{y}})$表示测试集样本中真实值与预测值之间的协方差，Var(y)表示测试集样本中真实值的方差，$\operatorname{Var}(\hat{\boldsymbol{y}}) $表示测试集样本中预测值的方差，式(6)中的y和$ \overline{\hat{y}}$由下式给出，

$ \left\{\begin{array}{l} \mathrm{MAE}=\frac{\sum\limits_{i=1}^N \sum\limits_{j=1}^M\left|y_{i j}-\hat{y}_{i j}\right|}{N M}=\frac{\sum\limits_{i=1}^N\left\|\boldsymbol{y}_i-\hat{\boldsymbol{y}}_i\right\|_1}{N M}, \\ \mathrm{MSE}=\frac{\sum\limits_{i=1}^N \sum\limits_{j=1}^M\left|y_{i j}-\hat{y}_{i j}\right|^2}{N M}=\frac{\sum\limits_{i=1}^N\left\|\boldsymbol{y}_i-\hat{\boldsymbol{y}}_i\right\|_2{}^2}{N M}, \\ \mathrm{RMSE}=\sqrt{\frac{\sum\limits_{i=1}^N \sum\limits_{j=1}^M\left|y_{i j}-\hat{y}_{i j}\right|^2}{N M}}, \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\sqrt{\frac{\sum\limits_{i=1}^N\left\|\boldsymbol{y}_i-\hat{\boldsymbol{y}}_i\right\|_2{}^2}{N M}}, \\ R=\frac{\operatorname{Cov}(\boldsymbol{y}, \hat{\boldsymbol{y}})}{\sqrt{\operatorname{Var}(\boldsymbol{y}) \operatorname{Var}(\hat{\boldsymbol{y}})}} \\ =\frac{\sum\limits_{i=1}^N \sum\limits_{j=1}^M\left(y_{i j}-\bar{y}\right)\left(\hat{y}_{i j}-\overline{\hat{y}}\right)}{\sqrt{\left(\sum\limits_{i=1}^N \sum\limits_{j=1}^M\left(y_{i j}-\bar{y}\right)^2\right)\left(\sum\limits_{i=1}^N \sum\limits_{j=1}^M\left(\hat{y}_{i j}-\overline{\hat{y}}\right)^2\right)}}, \end{array}\right. $

(6)

$ \bar{y}=\frac{\sum\limits_{i=1}^N \sum\limits_{j=1}^M y_{i j}}{N M}, \overline{\hat{y}}=\frac{\sum\limits_{i=1}^N \sum\limits_{j=1}^M \hat{y}_{i j}}{N M} . $

(7)

分别表示y和$\hat{\boldsymbol{y}} $的均值。

模型在经过测试集的评估之后，如果泛化能力达到了要求，即评价指标MAE、RMSE、R在设定的精度范围内，那么训练好的模型就可以用来生成实际缺失的数据，对缺失的帆板温度遥测数据进行插补。为对实际的插值效果进行评估，需要定量的计算，但是由于实际数据的缺失，无法像在测试集中计算3个指标一样计算范数$L_1\left(\boldsymbol{y}_i-\hat{\boldsymbol{y}}_i\right) $与$L_2\left(\boldsymbol{y}_i-\hat{\boldsymbol{y}}_i\right) $。假定帆板温度遥测数据有一段缺失，取缺失数据之前连续的时序数据构成模型输入x′_u，如下所示，

$ \boldsymbol{x}_u^{\prime}=\left(x_{u 1}^{\prime}, x_{u 2}^{\prime}, \cdots, x_{u D}^{\prime}\right)^{\mathrm{T}}, $

(8)

其中D表示模型输入序列的长度，同时取实际的缺失数据序列$\boldsymbol{y}_u^{\prime} $，如下所示，

$ \begin{gathered} \boldsymbol{y}_u^{\prime}=\left(y_{u 1}^{\prime}, y_{u 2}^{\prime}, \cdots, y_{u M}^{\prime}\right)^{\mathrm{T}} \\ =\left(*, *, \cdots, y^{\prime}{}_{u(k+1)}, \cdots, y_{u M}^{\prime}\right)^{\mathrm{T}} . \end{gathered} $

(9)

其中M表示模型输出序列的长度，k表示序列中缺失值的个数，$\boldsymbol{y}_u^{\prime} $前面k个缺失值使用*表示。

模型输入$\boldsymbol{x}_u^{\prime} $后会生成一段预测的用以插值的序列$ \hat{\boldsymbol{y}}_u^{\prime}$，如下所示

$ \hat{\boldsymbol{y}}_u^{\prime}=\left(\hat{y}_{u 1}^{\prime}, \hat{y}_{u 2}^{\prime}, \cdots, \hat{y}_{u M}^{\prime}\right)^{\mathrm{T}} . $

(10)

为计算实际缺失序列$\boldsymbol{y}_u^{\prime} $与模型输出序列$ \hat{\boldsymbol{y}}_u^{\prime}$之间的差异，引入带缺失值的范数$L_p^{\prime} $，用来表示$\boldsymbol{y}_u^{\prime} $和$ \hat{\boldsymbol{y}}_u^{\prime}$都存在的部分之间的差异。即经过插值填补之后，缺失序列$\boldsymbol{y}_u^{\prime} $中原本就存在的M-k个值与插补序列$ \hat{\boldsymbol{y}}_u^{\prime}$相对应的M-k个值之间的差异，L^′_p用来计算缺失序列和完整序列之间的差异大小，定义如下

$ L_p^{\prime}\left(\boldsymbol{x}^{\prime}\right)=\left\|\boldsymbol{x}^{\prime}\right\|_p{}^{\prime}=\left(\sum\limits_{v=k+1}^M\left|x^{\prime}{}_v\right|^p\right)^{\frac{1}{p}}. $

(11)

$ \left\{\begin{array}{l} \text {MAE}=\frac{\sum\limits_{u=1}^N \sum\limits_{v=k_u+1}^M\left|y_{u v}^{\prime}-\hat{y}_{u v}^{\prime}\right|}{N M-\sum\limits_{u=1}^N k_u}=\frac{\sum\limits_{u=1}^N\left\|\boldsymbol{y}_u^{\prime}-\hat{\boldsymbol{y}}_u^{\prime}\right\|_1^{\prime}}{N M-\sum\limits_{u=1}^N k_u}, \\ \mathrm{MSE}=\frac{\sum\limits_{u=1}^N \sum\limits_{v=k_u+1}^M\left|y_{u v}^{\prime}-\hat{y}_{u v}^{\prime}\right|^2}{N M-\sum\limits_{u=1}^N k_u}=\frac{\sum\limits_{u=1}^N\left\|\boldsymbol{y}_u^{\prime}-\hat{\boldsymbol{y}}_u^{\prime}\right\|_2^{\prime 2}}{N M-\sum\limits_{u=1}^N k_u}, \\ \operatorname{RMSE}=\sqrt{\frac{\sum\limits_{u=1}^N \sum\limits_{v=k_u+1}^M\left|y_{u v}^{\prime}-\hat{y}_{u v}^{\prime}\right|^2}{N M-\sum\limits_{u=1}^N k_u}} \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\sqrt{\frac{\sum\limits_{u=1}^N\left\|\boldsymbol{y}_u^{\prime}-\hat{\boldsymbol{y}}_u^{\prime}\right\|_2^{\prime 2}}{N M-\sum\limits_{u=1}^N k_u}}, \\ R=\frac{\operatorname{Cov}\left(\boldsymbol{y}^{\prime}, \hat{\boldsymbol{y}}^{\prime}\right)}{\sqrt{\operatorname{Var}\left(\boldsymbol{y}^{\prime}\right) \operatorname{Var}\left(\hat{\boldsymbol{y}}^{\prime}\right)}} \\ =\frac{\sum\limits_{u=1}^N \sum\limits_{v=k_u+1}^M\left(y_{u v}^{\prime}-\bar{y}^{\prime}\right)\left(\hat{y}_{u v}^{\prime}-\bar{\hat{y}}^{\prime}\right)}{\sqrt{\left(\sum\limits_{u=1}^N \sum\limits_{v=k_u+1}^M\left(y_{u v}^{\prime}-\bar{y}^{\prime}\right)^2\right)\left(\sum\limits_{u=1}^N \sum\limits_{v=k_u+1}^M\left(\hat{y}_{u v}^{\prime}-\overline{\hat{y}}^{\prime}\right)^2\right)}} . \end{array}\right. $

(12)

$ \bar{y}^{\prime}=\frac{\sum\limits_{u=1}^N \sum\limits_{v=k_u+1}^M y_{u v}^{\prime}}{N M-\sum\limits_{u=1}^N k_u}, \bar{\hat{y}}^{\prime}=\frac{\sum\limits_{u=1}^N \sum\limits_{v=k_u+1}^M \hat{y}_{u v}^{\prime}}{N M-\sum\limits_{u=1}^N k_u} . $

(13)

其中$\boldsymbol x^{\prime}=\boldsymbol y_u^{\prime}-\hat{\boldsymbol y}_u^{\prime} $。

在引入改进后的针对计算缺失数据和完整数据之间差异的范数计算方法之后，那么MAE、MSE、RMSE、R的计算方法也将会有变化，如式(12)和式(13)所示。用$\boldsymbol{y}_u^{\prime} $和$\hat{\boldsymbol{y}}_u^{\prime} $分别表示实际缺失数据集中第u个样本对应的真实标记和模型输出，并用k_u表示$\boldsymbol{y}^{\prime}{}_u $中缺失值的个数，v表示$\boldsymbol{y}^{\prime}{}_u $和$\hat{\boldsymbol{y}}^{\prime}{ }_u $中的第v维，N和M分别表示实际缺失样本集的样本数目和$\boldsymbol{y}^{\prime}{}_u $、$\hat{\boldsymbol{y}}^{\prime}{ }_u $的维度，$ \sum_{u=1}^N k_u$表示实际缺失样本集对应的真实标记矩阵中缺失值的个数，y′和$\hat{\boldsymbol{y}}^{\prime} $分别表示实际缺失样本集对应的真实标记矩阵和模型输出矩阵，y′和$ \bar{\hat y}^{\prime}$分别表示两矩阵均不缺失数据处的各自的均值。

3.2 仿真结果分析

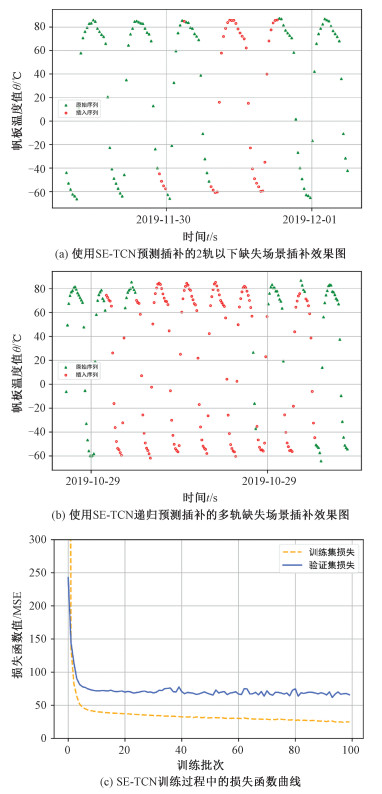
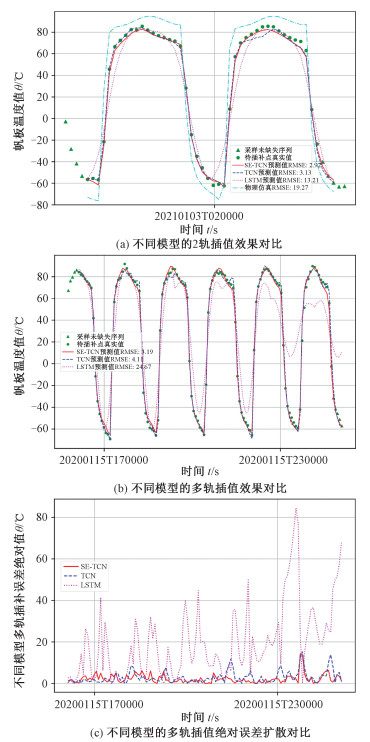
本文模型采用SE-TCN对从连续5轨的历史数据到未来连续2轨时序数据的映射进行拟合。相关训练集、测试集也据此进行构建。图 7(a)是使用SE-TCN模型对2轨(含)以下的某缺失场景进行预测插补的效果图，这类插补场景占据所有缺失场景的98.64%；图 7(b)则是递归使用SE-TCN模型对某多轨(2轨以上)缺失场景进行预测插补的效果图，这类插补场景占据所有缺失场景的1.36%。图 7(c)是SE-TCN训练过程中的损失函数曲线，橙黄色虚线和蓝色实线分别代表随着训练批次的增加，训练集和验证集分别对应的损失函数曲线。可以看到随着训练批次的增加，两者的损失函数都以近似指数的形式下降。图 8是不同模型的插值效果对比。其中图 8(a)是针对某2轨缺失场景的不同模型插值效果对比，从图中结果分析可以看出SE-TCN、TCN、LSTM、物理模型的插值效果依次降低，其中物理模型由于建模时未能全面考虑太空干扰因素，插值效果最差；图 8(b)是针对某多轨缺失场景(5轨)的不同模型插值效果对比，图 8(c)则是该场景下的绝对误差扩散图。由于物理仿真结果同神经网络对比差距太大，此处只对3种神经网络进行插值对比，因为模型结构是针对绝大多数的缺失场景构建的，模型输入输出长度确定，即根据历史5轨数据预测未来2轨数据。那么在多轨缺失场景下是通过递归调用模型对缺失值进行插补的，每次模型的输出都将作为下一次模型输入的一部分。在这种情况下，随着多轨插补的进行，误差会逐渐积累。但是由于多轨缺失场景占比很少，多轨插补带来的累计误差并不大。相比于SE-TCN和TCN，LSTM的多轨插补劣势明显，其误差扩散更快，而SE-TCN估计误差比TCN更小，多轨插补效果更好。针对2轨(含)以下的缺失场景和多轨缺失场景，SE-TCN均表现出良好的插值效果。

3.3 模型参数及不同模型插值效果

表 2为SE-TCN、TCN、LSTM 3个模型的参数，其中TCN除了不含有SE模块以外，其余参数和SE-TCN相同。SE模块仅有一个缩放参数r，而1.3节的W×H×C，其中W在本模型中为常值1，因为这是计算机视觉中SE模块在二维时序场景下的应用，H代表模型输入长度，即5轨采样点个数，C表示经过残差块之后每个采样点的维度大小，是个变量。表 3表示LSTM、TCN、SE-TCN 3种模型在测试集和实际缺失数据集上的评价指标值，测试集相关指标计算方式由式(6)和式(7)确定，实际缺失数据集相关指标计算方式由式(12)和式(13)确定。对比不同模型分别在测试集和实际缺失数据集上的评价指标，可以看到使用SE-TCN模型进行卫星帆板遥测数据插值具有良好的效果。与LSTM和TCN模型相比，SE-TCN在测试集上的评价指标R分别提升2.59%、0.06%，MAE分别降低65.85%、12.28%，RMSE分别降低42.94%、2.17%；SE-TCN在实际缺失数据集上的评价指标R分别提升2.93%、0.04%，MAE分别降低56.35%、12.43%，RMSE分别降低35.42%、0.47%。

4 结束语

本文采用引入注意力机制的时间卷积网络SE-TCN对卫星帆板温度遥测数据进行插值填补。与卫星帆板物理模型仿真插补方法、传统统计学插补方法如线性插值和样条插值、常见的时间序列处理模型如LSTM、TCN等比较，获得了较好的插值填补效果。遥测数据进行插值填补之后可以得到较为完整的数据，方便对该时序数据进一步分析统计，进而对下一步的研究打下基础。