2. 西安交通大学航天航空学院 机械结构强度与振动国家重点实验室, 西安 710049
2. State Key Laboratory for Strength and Vibration of Mechanical Structures, School of Aerospace, Xi'an Jiaotong University, Xi'an 710049, China
液体射流的破碎广泛地存在于自然界及日常生产与生活当中,如雨水降落、喷墨打印、发动机燃油喷射等[1-2],其中蕴含的丰富物理现象及复杂的机理一直吸引着流体力学研究者的关注。Plateau[3]率先对下落的液体射流进行了实验研究。随后,Rayleigh[4-5]、Weber[6]、Ohnesorge [7] 等人分别从数学描述、液体黏性和高出射速度方面完善并发展了液体射流破碎的理论体系。后续的研究者相继引入2个典型的无量纲参数来表征射流动力学过程,即韦伯数We和奥内佐格数Oh,其中We表示惯性力与表面张力的比值,Oh表示黏性力、惯性力和表面张力之间的关系。其定义分别为
在研究射流的破碎现象时,破碎长度,即射流与喷嘴之间保持连接的最小距离,是表征射流破碎特性的重要参数。以往的研究者们对液体射流的破碎长度进行了大量的实验或数值研究[9-14]。Hiroyasu[15]提出,对于液体射流,毛细不稳定性在低速时占主导,剪切不稳定性在高速时占主导。由毛细不稳定性主导的破碎长度与We1/2成正比。由剪切不稳定性主导的破碎长度则完全取决于射流和周围介质的密度比。Lin和Reitz[8]提出了射流破碎长度随速度的变化规律,即随着速度的增大,射流的破碎长度先增大后减小。其中Rayleigh模式下的破碎长度是随速度的增大而线性增大,一阶风致模式下的破碎长度达到最大值,之后开始减小。
近年来,液态金属作为冶金、喷涂、3D打印和核聚变反应堆的材料,因其优良的物理化学性质吸引了越来越多研究者的关注。特别是在磁约束核聚变反应堆中,以射流方式形成的液态金属自由表面流因具有可承受较高的中子辐照和表面热负荷、循环可更新、无寿命限制等优点,有望成为未来液态偏滤器/限制器的一种方式,而聚变堆中的强磁场环境则对其中流动的液态金属产生极强的磁流体动力学效应,造成流动的受阻与飞溅,至今仍没有很好的控制方法。对磁场影响下液态金属射流特性的研究,能为聚变堆液态金属偏滤器/限制器设计提供理论支撑。Ohgo等[16]以水代替熔融的锡金属,发现插入内部流动阻力插件可以阻止射流破碎形成液滴。Oshima等[17]以液态汞为工质,研究了非均匀磁场下射流的截面形状变化,发现其截面宽高比随相互作用数
本文中,我们采用高速摄影系统,进行无磁场及水平磁场下液态镓铟锡合金的三维自由射流实验。首先,选取射流过程中的典型图像,以显示不同We下的射流形态。之后,使用编制的MATLAB代码处理这些图像,最终获得射流的表面扰动及破碎长度的变化,并重点对比了有无磁场时破碎长度变化的不同规律。我们选择表示洛伦兹力与黏性力比值的哈特曼数
对于磁场下的流体实验而言,工质流体的导电性直接决定实验现象的明显与否。因此,汞、镓和镓合金等高导电性的液态金属无疑成为优选。其中,汞易蒸发且少量汞蒸气便会对人体造成伤害,而液态镓易结晶(熔点为29.8 ℃),故室温下液态且无毒的镓合金成为我们的首选。本实验中,选择由质量分数为67 % 的镓、20.5 % 的铟和12.5 % 的锡组成的共晶合金镓铟锡(GaInSn)作为工作流体,其物理特性如表 1所示[21]。但GaInSn合金极易氧化,当其直接暴露在氧气浓度超过1×10-6的气体环境中氧化便会发生[22]。实验发现,一旦发生氧化,由于包裹在射流表面的氧化物的表面张力急剧下降,GaInSn射流将不再被夹断形成液滴。本实验中,在有机玻璃材质的实验段顶盖上设计了两个独立的导气管:一支深入到实验段底部,用以通入氩气; 另一支从盖顶向外,使得空气得以排出。由此形成纯氩环境,有效地解决了GaInSn的氧化问题。
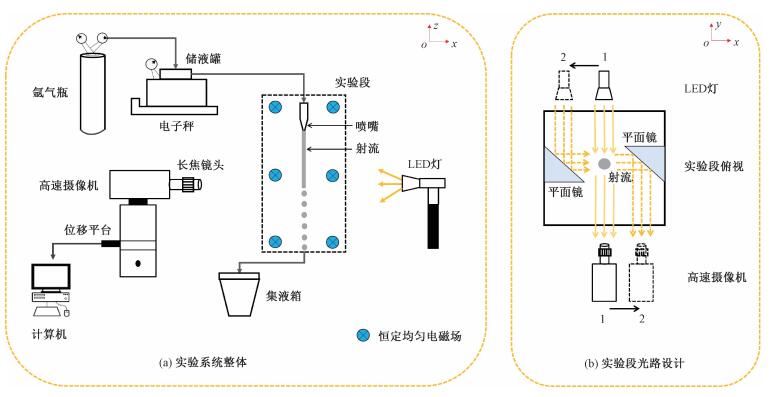
1.2 实验装置本实验装置主要包括恒定的磁场系统、射流发生系统、充有氩气保护的射流实验段和高速摄影系统4个部分,如图 1(a)所示。恒定的磁场系统能产生最大磁场强度2T,最大不均匀度低于5 % 的水平恒定磁场。由储液罐及氩气瓶组成的压力驱动系统可产生最大速度9.3 m/s的液体射流,以氩气为驱动气体则可有效防止GaInSn的氧化。由高速摄像机(Vision Research, Inc., Phantom V341)、LED光源和位移平台组成的高速摄影系统则可实现射流形态的采集。通过位移平台的高度和图形处理所得破碎长度相加,可得到真实的射流破碎长度。通过电子秤测得质量流量,转化为喷嘴出口处的平均射流速度。由有机玻璃制成的实验段顶盖带有2支导气管,其中一支伸入到腔体内部底端,用以通入氩气,另一支指向腔体顶盖外侧,用以排出气体。对于氩气环境的营造,按照“实验前大流量排出、实验中极小流量保护”的原则,在实验前用较大流量持续排净实验段内空气,创造纯氩环境,之后改用极其微弱的氩气流用以维持。实验过程中氩气流量非常小,其所产生的气动作用力较之射流惯性所引起的周围气体作用而言可以忽略。由此我们认为,由氩气环境取代空气环境,仅起到防止GaInSn氧化的作用,不影响射流自身的破碎过程。在射流轮廓拍摄方面,在实验段侧壁上安装了一对45°角的平面反射镜,如图 1(b)所示。当相机及光源置于1-1位置时实现x方向(垂直磁场线)的拍摄,当相机及光源置于2-2位置时实现y方向(沿磁场线)的拍摄。本套装置中,高速摄像机和LED灯相向置于x方向,水平磁场沿y方向,射流速度沿z方向。
|
Download:
|
| 图 1 实验系统示意图 Fig. 1 Schematic diagram of the experimental system | |
为防止镓铟锡的氧化,在每次实验操作开始前,我们均向实验段中通入氩气并持续一段时间,以完全排净实验系统中的氧气。之后在不同驱动压力和不同磁场强度下依次进行实验。在正式采集数据前,我们需要等待一段时间以保证实验前射流处于充分发展,这可以通过高速摄像机视野中实时显示的射流状态进行判断。在完成垂直磁场线方向的数据采集后,迅速将高速摄像机和光源的同步调整到2-2的位置,进行沿磁场线方向的数据采集。在这个过程中,储液罐及所有阀门均都保持不动,从而确保两个方向的数据均为在相同压力、相同磁场强度下的同一束射流。在获得全部实验数据后,我们用自编的MATLAB代码处理所得图像。特别是,在统计破碎长度时采用了取平均的方法,从而减少了射流波动的影响,这种待射流充分发展后取平均的方法,也是前人研究中处理射流破碎长度时广泛采用的[23-25]。
2 结果和讨论 2.1 射流形态在无磁场的情况下,GaInSn射流形态随We的变化如表 2所示。当We=31时,射流破碎形成相同大小的球形液滴,表明其破碎处于由Plateau-Rayleigh不稳定性主导的典型Rayleigh模式,随后破碎逐渐过渡到一阶风致模式。卫星液滴在We=62时开始出现,并在We=134时出现大小不一的尺寸。与液滴破碎不同,射流在We=134时开始出现液丝破碎,这拓展了Rajendran等[26]对水、乙二醇和丙二醇的液滴-液丝破碎临界We实验结果。当We=206时,射流发生二次膨胀,即不同于一个波长发生一次膨胀并形成一个液滴,此处一个波长上可以观察到明显的两次膨胀。随着We的继续增大,射流和周围气体间的作用逐渐加剧,不规则液滴和纺锤形液滴相继在We=244和We=355时出现。当We=388时,射流不再明显地被夹断成液丝或液滴。
|
|
表 2 无磁场时的射流形态 Table 2 Jet morphology without a magnetic field |
当施加水平磁场后,GaInSn射流形态变得更加复杂,特别是破碎点以下的液滴部分。表 3显示了强磁场下GaInSn液滴的几种典型形态。对于球形液滴,竖直平面内互相垂直的液滴速度与磁场必将产生水平平面内的感应电流,感应电流则在磁场的作用下在竖直平面内产生与速度方向相反的洛伦兹力,由于在流动方向上受向上的洛伦兹力及向下的惯性力共同作用,球形液滴在流动方向上发生拉长,形成椭球形液滴。同时,GaInSn射流出现次级液滴的分离与融合现象,即小液滴从流向上方的大液滴分离出来,并融合到下面一个大液滴上。对于卫星液滴,其对应的主液滴受磁场影响形成了不规则形状,同时也出现了一次性多个液滴的倍增情形,由于卫星液滴的出现是射流破碎非线性效应的结果,这表明由于磁场环境产生的洛伦兹力促进了射流破碎过程的非线性效应的产生。当从正侧两个不同方向观察射流时,射流的前缘呈现出不同的形状,如表 4所示。在垂直磁场线的方向,射流的前缘呈现扁平状,而在沿磁场线的方向,射流的前缘呈现椭圆状。于星星等[27]通过水平磁场下锂射流的数值模拟得到了同样的结论,并从洛伦兹力和表面张力之间的相互作用上解释了这一变化。通过对射流内部速度分析发现射流前缘形状发生该变化的原因是:在垂直磁场线方向,速度核心区呈较宽的长条状,在平行磁场线方向,速度核心区呈细窄线状。
|
|
表 3 水平强磁场下的射流形态(B=1.5T) Table 3 Jet morphology under a strong horizontal magnetic field (B =1.5T) |
|
|
表 4 水平磁场下的射流前缘(B=0.75 T) Table 4 Front edge of the jet in a horizontal magnetic field (B=0.75T) |
当施加磁场时,实验中射流表面的扰动变得无序且不规则,故本节仅考察无磁场时的情形。GaInSn射流的表面扰动共呈现膨胀波、正弦波两种扰动形态,如表 5所示。膨胀波由Plateau-Rayleigh不稳定引发,上下表面位移反相[28];正弦波是由空气动力效应引发,上下表面位移同相[29]。当We不超过143时,扰动均以膨胀波形式出现,当We达到355时,则可明显观察到正弦波形式的扰动。由此推断,膨胀波到正弦波的转化过程内必然存在一个过渡的We范围。此外,正弦波出现必将伴随有膨胀波的出现,即膨胀波始终存在,而正弦波只有在We相对较大、空气动力效应显著时才会出现。这与于星星等[27]所述正弦波比膨胀出现频率低的结论是一致的。
|
|
表 5 无磁场时射流表面扰动形态 Table 5 Patterns of jet surface disturbance without a magnetic field |
图 2展示了无磁场时射流表面振幅随We的变化规律。随着We的增加,射流的表面振幅先减小后增大。随着We由31增大至62,表面张力对射流的破碎由Plateau-Rayleigh不稳定性中的促进作用变为阻碍作用,表面幅度值显着降低。表面张力的这种双重作用体现在:一方面阻止射流的表面积增加进而阻碍其破碎,一方面释放液体的表面能,使得射流更易破碎形成液滴[30]。随着We进一步增大,气动作用力的影响开始显现,并与表面张力互相竞争。逐渐地,气动作用力胜出并主导破碎过程,表面振幅逐渐增大且增速越来越快。因此,在We=134后,GaInSn射流在气动作用力的作用下失稳加速。

|
Download:
|
| 图 2 无磁场时GaInSn射流表面扰动随We的变化 Fig. 2 Variation of surface disturbance with We without a magnetic field | |
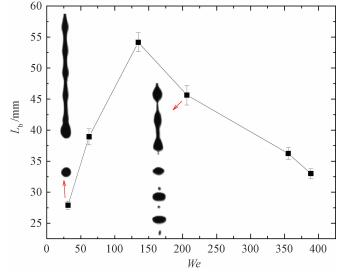
图 3展示了在无磁场的情况下,GaInSn射流破碎长度的变化。随着We的增大,射流的破碎长度整体呈现出先增大后减小的趋势,这与Lin和Reitz[8]所得结论一致。破碎长度在We=134时达到最大值,该点也正是表面扰动幅度最小的点。在破碎长度增长段,射流在表面张力的主导下破碎形成液滴;随着破碎机制由Rayleigh模式过渡到一阶风致模式,破碎长度在气动作用力的影响下逐渐减小。进一步地,我们定义无量纲破碎长度
|
Download:
|
| 图 3 无磁场时GaInSn射流破碎长度随We的变化 Fig. 3 Variation of breakup length with We without a magnetic field | |
|
Download:
|
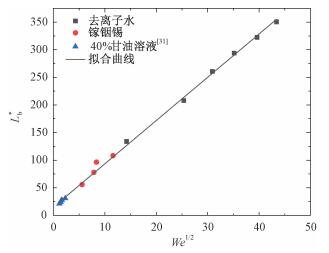
| 图 4 P-R不稳定机制下不同种类流体破碎长度随We1/2的变化 Fig. 4 Variation of breakup length with We1/2 for different types of fluids under P-R instability | |
图 5展示了施加磁场前后射流破碎长度变化的对比。可以看出无论有无磁场,射流的破碎长度均在一定范围内存在波动。在We=31时,起初两者的破碎长度没有明显的差别,但随着时间的推进,1.5 T强磁场下的破裂长度最终会明显大于无磁场时的破裂长度。通过改变We数和Ha数,获得不同参数下的射流破碎长度,并将数据绘制于图 6。实验数据整体表明磁场的存在增加了液态金属射流的破裂长度,这证实了于星星等[27]在小We时数值模拟的结论。然而,在一些参数区间:约172 < We < 385时,云图中出现了明显的向下凹陷,这表明在特定的We,磁场的存在反而会减弱破碎长度的增大。Yang等[32]对磁场下GaInSn液滴的实验和数值研究表明,这种磁场影响的效果可能与射流内存在的感应电流及产生的电磁力有关。但对造成射流该种变化的原因还需未来进一步的实验及数值研究。

|
Download:
|
| 图 5 有、无磁场下射流破碎长度随时间的动态变化 Fig. 5 Dynamics of breakup length with time in the presence and absence of a magnetic field | |

|
Download:
|
| 图 6 破碎长度随We及Ha的变化云图 Fig. 6 Variation of breakup length with We and Ha | |
本文采用高速摄影系统研究有无磁场影响下GaInSn三维自由射流的破碎特征。对于无磁场的情况,观察到不同We下射流的形态,提出We=134作为非液丝破碎和液丝破碎的临界。无磁场时射流的表面扰动呈现出膨胀波和正弦波两种不同形态。在表面张力和气动作用力的共同作用下,射流的表面扰动振幅随We的增大而先减小后增大,破碎长度随We的增大而先增大后减小。在较小We下,射流的破碎长度与We1/2成正比,且不受工质流体的影响。对于水平磁场的情况,观察到与无磁场时完全不同的射流形态,射流破碎后形成沿流向拉长的椭球形液滴、先分离后融合的次级液滴、倍增的卫星液滴及不规则形状的主液滴。射流前缘在垂直磁场线方向呈扁平状,沿磁场线方程呈椭圆状。随着Ha数的增大,射流破碎长度整体上呈现增长趋势,但在部分工况下会出现减小的现象。本文的结果为磁流体动力学效应下的射流稳定性研究提供了一定的参考。
| [1] |
Eggers J, Villermaux E. Physics of liquid jets[J]. Reports on Progress in Physics, 2008, 71(3): 036601. Doi:10.1088/0034-4885/71/3/036601 |
| [2] |
Sterling A M, Sleicher C A. The instability of capillary jets[J]. Journal of Fluid Mechanics, 1975, 68(3): 477-495. Doi:10.1017/s0022112075001772 |
| [3] |
Plateau J A F. Statique expérimentale et théorique des liquides soumis aux seules forces moléculaires[M/OL]. Gauthier-Villars, 1873: 261-266[2022-03-28]. https://openlibrary.org/books/OL23535127M.
|
| [4] |
Rayleigh L. On the instability of jets[J]. Proceedings of the London Mathematical Society, 1878(1): 4-13. Doi:10.1112/plms/s1-10.1.4 |
| [5] |
Rayleigh L. On the capillary phenomena of jets[J]. Proceedings of the Royal Society, 1879, 29(196): 71-97. Doi:10.1098/rspl.1879.0015 |
| [6] |
Weber C. Zum zerfall eines flüssigkeitsstrahles[J]. ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift Für Angewandte Mathematik Und Mechanik, 1931, 11(2): 136-154. Doi:10.1002/zamm.19310110207 |
| [7] |
Ohnesorge W V. Die bildung von tropfen an düsen und Die auflÖsung flüssiger strahlen[J]. ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift Für Angewandte Mathematik Und Mechanik, 1936, 16(6): 355-358. Doi:10.1002/zamm.19360160611 |
| [8] |
Lin S P, Reitz R D. Drop and spray formation from a liquid jet[J]. Annual Review of Fluid Mechanics, 1998, 30: 85-105. Doi:10.1146/annurev.fluid.30.1.85 |
| [9] |
Eroglu H, Chigier N, Farago Z. Coaxial atomizer liquid intact lengths[J]. Physics of Fluids A: Fluid Dynamics, 1991, 3(2): 303-308. Doi:10.1063/1.858139 |
| [10] |
SHIBATA K, KOSHIZUKA S, OKA Y. Numerical analysis of jet breakup behavior using particle method[J]. Journal of Nuclear Science and Technology, 2004, 41(7): 715-722. Doi:10.1080/18811248.2004.9715538 |
| [11] |
Xie L, Yang L J, Ye H Y. Instability of gas-surrounded Rayleigh viscous jets: Weakly nonlinear analysis and numerical simulation[J]. Physics of Fluids, 2017, 29(7): 074101. Doi:10.1063/1.4991578 |
| [12] |
Fenn R W I, Middleman S. Newtonian jet stability: the role of air resistance[J]. AIChE Journal, 1969, 15(3): 379-383. Doi:10.1002/aic.690150315 |
| [13] |
Etzold M, Deswal A, Chen L, et al. Break-up length of liquid jets produced by short nozzles[J]. International Journal of Multiphase Flow, 2018, 99: 397-407. Doi:10.1016/j.ijmultiphaseflow.2017.11.006 |
| [14] |
Spangler C A, Hilbing J H, Heister S D. Nonlinear modeling of jet atomization in the wind-induced regime[J]. Physics of Fluids, 1995, 7(5): 964-971. Doi:10.1063/1.868572 |
| [15] |
Hiroyasu H. Break-up length of a liquid jet and internal flow in a nozzle[C/OL]. Proc. 5th. ICLASS. 1991: 275-282[2022-03-28]. https://www.researchgate.net/publication/284773688.
|
| [16] |
Ohgo T, Miyazawa J, Goto T, et al. Study on jets stabilized by inserting internal flow resistances for the liquid metal divertor in the helical fusion reactor[J]. Plasma and Fusion Research, 2018, 13: 1405003. Doi:10.1585/pfr.13.1405003 |
| [17] |
Oshima S, Yamane R, Mochimaru Y, et al. The shape of a liquid metal jet under a non-uniform magnetic field[J]. JSME International Journal, 1987, 30(261): 437-448. Doi:10.1299/jsme1987.30.437 |
| [18] |
许增裕, 潘传杰, 康伟山, 等. 几种液体金属自由表面的MHD不稳定性实验研究[J]. 核聚变与等离子体物理, 2008, 28(4): 289-292. Doi:10.16568/j.0254-6086.2008.04.006 |
| [19] |
Kuteev B V, Sergeev V Y, Krylov S V, et al. Conceptual analysis of a tokamak reactor with lithium dust jet[J]. Nuclear Fusion, 2010, 50(7): 075001. Doi:10.1088/0029-5515/50/7/075001 |
| [20] |
Halfon S, Arenshtam A, Kijel D, et al. High-power liquid-lithium jet target for neutron production[J]. The Review of Scientific Instruments, 2013, 84(12): 123507. Doi:10.1063/1.4847158 |
| [21] |
Morley N B, Burris J, Cadwallader L C, et al. GaInSn usage in the research laboratory[J]. The Review of Scientific Instruments, 2008, 79(5): 056107. Doi:10.1063/1.2930813 |
| [22] |
Liu T Y, Sen P, Kim C J. Characterization of nontoxic liquid-metal alloy galinstan for applications in microdevices[J]. Journal of Microelectromechanical Systems, 2012, 21(2): 443-450. Doi:10.1109/JMEMS.2011.2174421 |
| [23] |
Trettel B. Reevaluating the jet breakup regime diagram[J]. Atomization and Sprays, 2020, 30(7): 517-556. Doi:10.1615/atomizspr.2020033171 |
| [24] |
Jung W H, Park H S, Moriyama K, et al. Analysis of experimental uncertainties in jet breakup length and jet diameter during molten fuel-coolant interaction[J]. Nuclear Engineering and Design, 2019, 344: 183-194. Doi:10.1016/j.nucengdes.2019.01.018 |
| [25] |
Shimizu M, Arai M, Hiroyasu H. Measurements of breakup length in high speed jet[J]. Bulletin of JSME, 1984, 27(230): 1709-1715. Doi:10.1299/jsme1958.27.1709 |
| [26] |
Rajendran S, Jog M A, Manglik R M. Experimental investigation of jet breakup at low weber number[J]. Atomization and Sprays, 2017, 27(9): 821-834. Doi:10.1615/atomizspr.2017019424 |
| [27] |
于星星, 张杰, 倪明玖. 水平磁场中液态金属射流的三维数值研究[J]. 中国科学院大学学报, 2019, 36(4): 481-486. Doi:10.7523/j.issn.2095-6134.2019.04.006 |
| [28] |
Breslouer O. Rayleigh-Plateau Instability: Falling Jet[R/OL].(2010-08-01)[2022-03-28]. http://www.princeton.edu/~stonelab/Teaching/Oren%20Breslouer%20559%20Final%20Report.pdf.
|
| [29] |
Squire H B. Investigation of the instability of a moving liquid film[J]. British Journal of Applied Physics, 1953, 4(6): 167-169. Doi:10.1088/0508-3443/4/6/302 |
| [30] |
李帅兵, 司廷. 射流破碎的线性不稳定性分析方法[J]. 空气动力学学报, 2019, 37(3): 356-372. Doi:10.7638/kqdlxxb-2018.0153 |
| [31] |
Omocea I L, Patrascu C, Turcanu M, et al. Breakup of liquid jets[J]. Energy Procedia, 2016, 85: 383-389. Doi:10.1016/j.egypro.2015.12.265 |
| [32] |
Yang J C, Qi T Y, Han T Y, et al. Elliptical spreading characteristics of a liquid metal droplet impact on a glass surface under a horizontal magnetic field[J]. Physics of Fluids, 2018, 30(1): 012101. Doi:10.1063/1.5000054 |
 2022, Vol. 39
2022, Vol. 39 












